В системах связи с импульсной модуляцией переносчиком Информации служит периодическая последовательность импульсов одинаковой формы

(3.42)

где U(t) — нормированная функция, характеризующая форму импульса; A0 — амплитуда импульса; — начало переднего фронта k-го импульса ;— период следования импульсов; — начало отсчета последовательности; — длительность k-го импульса, отсчитываемая на некотором заданном уровне.

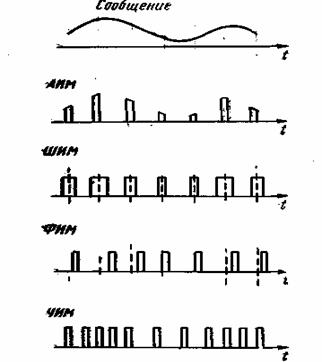
3.7. Сигналы при различных видах импульсной модуляции

При модуляции один из параметров последовательности изменяется в соответствии с передаваемым сообщением (рис. 3.7). Так, при амплитудно-импульсной модуляции (АИМ) изменяется амплитуда импульса А:

(3.43)

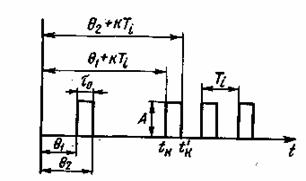
Рис. 3.8. Параметры периодической последовательности прямоугольных импульсов

При широтно-импульсной модуляции (ШИМ) изменяется длительность импульса

(3.44)

где — максимальное отклонение фронта импульсов в одну сторону.

При фазовой импульсной модуляции (ФИМ) изменяется сдвиг импульсов относительно тактовых точек .

(3.45)

При частотно-импульсной модуляции (ЧИМ) в соответствии с передаваемым сообщением изменяется частота следования импульсов.

Так же, как и при ФИМ, импульсы сдвигаются относительно тактовых точек, но в другой закономерности. Различие между ФИМ и ЧИМ аналогично различию между ФМ и ЧМ синусоидального переносчика.

Периодическую последовательность прямоугольных импульсов (рис. 3.8) можно записать в следующем виде:

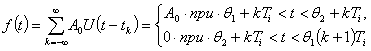(3.46)

Такую последовательность импульсов можно представить рядом Фурье. В соответствии с выражениями (2.67) и (2.68) имеем

,где ,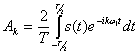

В нашем случае

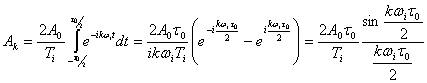(3.47)

тогда

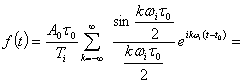
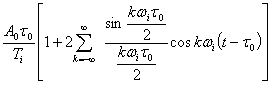(3.48)

где

2я

Спектр амплитуд периодической последовательности прямоугольных импульсов приведен на рис. 3.9. Амплитуды спектральных компонент определяются значениями модуля спектральной плотности || (3.47) на гармониках частоты повторения .Форма огибающей частотного спектра периодической последовательности определяется формой отдельного импульса. С увеличением периода повторения интервал частот между соседними спектральными компонентами сокращается, их число растет, а амплитуда каждой компоненты уменьшается при сохранении постоянного соотношения между ними. При неограниченном увеличении периодическая последовательность вырождается в одиночный импульс, а линейчатый спектр становится сплошным.

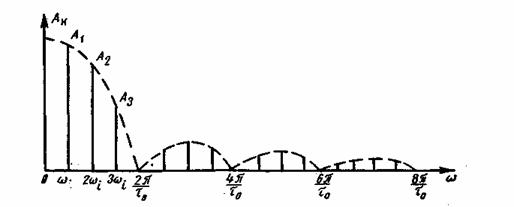
Рис. 3.9. Спектр периодической последовательности прямоугольных импульсов

Спектр периодической последовательности радиоимпульсов получается из спектра последовательности видеоимпульсов переносом шкалы частот на несущую частоту и дополнением полученного спектра его зеркальным отображением.

При модуляции параметры, входящие в выражения (3.46) и (3.48), являются функциями времени:. Модулированная последовательность будет представлять теперь уже непериодическую функцию, деформированную относительно исходной:

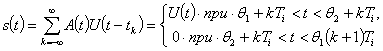(3.49)

или согласно (3.48)

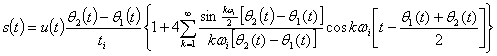(3.50)

Полученная формула определяет частотный спектр деформированной последовательности импульсов. Для получения спектров сигналов при различных видах модуляции в ф-лу (3.50) необходимо подставить соответствующее выражение модулированного параметра.

Для примера найдем спектр при АИМ. При модуляции одним тоном u(t)=sinΩ(t) и A=A0(1+msinΩt); остальные параметры последовательности неизменны:

После подстановки этих значений в (3.50) и несложных тригонометрических преобразований для частотного спектра АИМ сигнала получаем

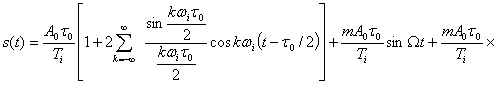
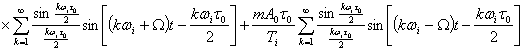(3.51)

На рис. 3.10 приведен график спектра АИМ сигнала. Сравнение его с рис. 3.9 показывает, что при АИМ модулируется по амплитуде каждая составляющая спектра немодулированной последовательности импульсов как изолированная «несущая». В спектре содержится низкочастотное модулирующее сообщение u(t) с частотой Ω, следовательно, демодуляция при АИМ может быть осуществлена с помощью фильтра нижних частот, пропускающего низкочастотное колебание u(t).

Аналогично определяется спектр и для других видов импульсной модуляции. Для вычисления спектра при ФИМ в (3.50) необходимо подставить выражение (3.45), определяющее изменение положения импульса в соответствии с передаваемым сообщением, а при ШИМ — выражение (3.44), определяющее изменение длительности импульса.

При импульсно-кодовой модуляции (ИКМ) передача отдельных значений сигнала сводится к передаче определенных групп импульсов. Эти группы передаются друг за другом через относительно большие промежутки времени по сравнению с длительностью отдельных импульсов. Каждая кодовая группа импульсов представляет собой регулярный непериодический сигнал, спектр которого может быть вычислен на основании преобразований Фурье обычным образом.

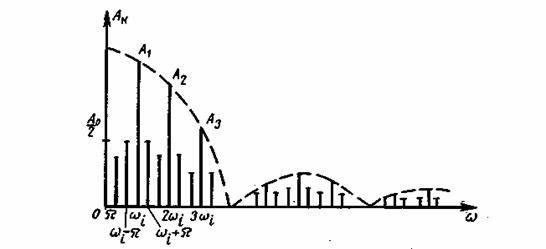
Рис. 3.10. Спектр АИМ сигнала

Ширина спектра последовательности импульсов практически не зависит от частоты повторения и определяется, главным образом, шириной спектра одного импульса. При наличии модуляции любого вида спектр расширяется незначительно за счет боковых частот крайних составляющих спектра немодулированных импульсов. Поэтому рабочая полоса частот, занимаемая импульсными сигналами, практически не зависит от вида модуляции и определяется длительностью и формой импульса.