Производительность источника определяется количеством информации, передаваемой в единицу времени. Измеряется производительность количеством двоичных единиц информации (бит) в секунду. Если все элементы сообщения имеют одинаковую длительность t, то производительность

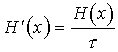. (10)

Если же различные элементы сообщения имеют разную длительность, то в приведённой формуле надо учитывать среднюю длительность , равную математическому ожиданию величины t :

.

Однако в последней формуле p(ti) можно заменить на p(xi) (вероятность i-го сообщения), так как эти вероятности равны. В результате получаем

, (11)

а производительность источника будет равна

. (12)

Mаксимально возможная производительность дискретного источника равна

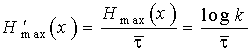. (13)

Для двоичного источника, имеющего одинаковую длительность элементов сообщения (k=2, ) имеем

бит¤с. (14)

При укрупнении алфавита в слова по n букв, когда k=2n, , имеем

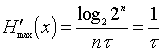бит¤с, что совпадает с формулой (14).

Таким образом, путём укрепления алфавита увеличить производительность источника нельзя, так как в этом случае и энтропия, и длительность сообщения одновременно возрастают в одинаковое число раз (n).

Увеличить производительность можно путём уменьшения длительности элементов сообщения, однако возможность эта ограничивается полосой пропускания канала связи. Поэтому производительность источника можно увеличить за счет более экономного использования полосы пропускания, например, путем применения сложных многоуровневых сигналов.

Вопросы

1. Что такое производительность дискретного источника, чему она равна?
2. Когда производительность источника максимальна, чему она равна?
3. Можно ли увеличить производительность источника путём укрупнения алфавита?
4. Как можно увеличить производительность источника при заданной длительности элементов сообщения?