8.2.1. ВКС с настроенным на последовательный резонанс выходным П -образным контуром

8.2.1.1. Расчет напряжений и токов в элементах П-образного контура и в элементе связи

8.2.1.2. Настройка колебательной системы

8.2.1.3. Описание алгоритма программ PLи PLС

8.2.1.4. Расчет анодного контура

8.2.2. ВКС с настроенным на последовательный резонанс выходным П-образным контуром при при максимуме КБВ на его входе

8.2.2.1. Расчет элементов колебательной системы

8.2.2.2. Настройка колебательной системы

8.2.2.3. Описание алгоритма программ PLK

8.2.1. ВКС с настроенным на последовательный резонанс выходным П-образным контуром

Эквивалентные схемы колебательной системы изображены на рис.8.10б и 8.10в, где r'_ф и х'_ф - активная и реактивная составляющие внесенного в П-контур входного сопротивления антенного фидера Z_вхф=r_ф± jx_ф, которые определяются (8.1):

,

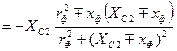
(8.31)

В этих формулах при емкостном характере сопротивления х_ф стоит знак «+», при индуктивном – знак «–». При такой настройке входное сопротивление его входной емкости С₁, а R₀ зависит от входного сопротивления антенного

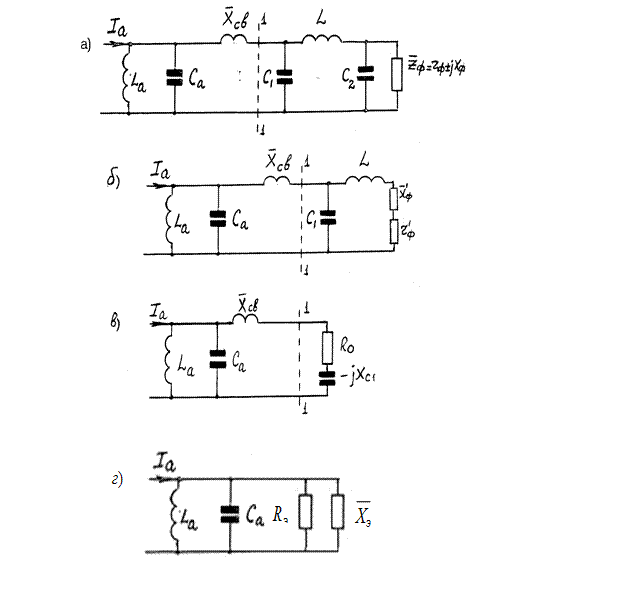
Рис.8.10

фидера и от параметров П–контура, которые должны быть выбраны так, чтобы при всех значениях составляющих входного сопротивления антенного фидера с заданными W и К₁ было возможно реализовать связь между контурами, обеспечивающую требуемую величину эквивалентного сопротивления R_э нагрузки ламп оконечного каскада. Величина R₀ равна:

R₀= , (8.32)

Реактивное сопротивление контурной катушки индуктивности L определяется формулой

X_L= X_C1+ , (8.33)

Сопротивление элемента связи:

Х_св = 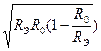Х_с1. , _. ...(8.34)

В формуле (8.34) знак «+» стоит при индуктивной связи, а знак «–»–при емкостной.

8.2.1.1. Расчет напряжений и токов в элементах П-образного контура и в элементе связи

Амплитуда переменного напряжения на элементе связи:

U_св = U_к× , (8.35)

Эффективное значение тока через элемент связи:

I_свefft = 0,707× (8.36)

Амплитуда переменного напряжения на входной емкости С₁ П-контура:

U_c1max = U_{вх max} = , (8.37)

где R_вх – активная составляющая входной проводимости П-контура:

R_вх = 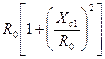. (8.38)

Трансформируемое элементом связи параллельно анодному контуру реактивное сопротивление Х_э, которое должно быть скомпенсировано при настройке анодного контура:

= j 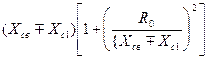, (8.39)

где верхний знак - при индуктивной связи между контурами, а нижний - при емкостной.

Значения емкостей конденсаторов и индуктивностей контурной катушки и элемента связи (если связь индуктивная) колебательной системы определяются формулами:

С(пФ) = , (8.40)

L(мкГ) = ,

причем, С_min рассчитывают при Х_Cmax и l_min, а C_max - при Х_Cmin и l_max; L_min рассчитывают при Х_Lmin и l_min, L_max - при Х_Lmax и l_max.

8.2.1.2. Настройка колебательной системы

Для настройки колебательной системы устанавливают слабую связь между контурами и настраивают вначале анодный контур, затем - выходной П-контур (по максимуму загрузки ламп конечного каскада). При этом обращается в нуль реактивная составляющая полного по обходу контура сопротивления (с учетом внесенного сопротивления нагрузки - входного сопротивления фидера с волновым сопротивлением W и КБВ К₁). Затем связь между контурами изменяют, после чего производят их подстройку до получения оптимального режима ламп оконечного каскада. Настройка П-контура производится изменением его индуктивности L (рис.8.10а).

Этот метод настройки является общепринятым для большинства мощных КВ передатчиков. При настройке ВКС мощность на ее выходе максимальна, поэтому в качестве индикатора настройки используют измеритель выходной мощности.

Программы PLC-1AМ, PLC-2AМ, PLC-2SB

1. Усиление мощности однотонового сигнала.

Наибольшее напряжение на входном конденсаторе С₁ П-контура определяется формулой:

U_c1max = ,

где Р- мощность в пиковом режиме, R_вхmax - наибольшее значение активной составляющей входной проводимости П – контура.

Наибольшее напряжение на конденсаторе С₂ равно:

U_c2max = ,

где R_вхфmax =W/K₁.

Эффективные значения токов в элементах П-контура равны:

в конденсаторе С_1:

I_c1eff = 0,707× U_c1max/X_c1 ,

в конденсаторе С₂:

I_c2eff = 0,707×U_c2max/X_c2 ,

в катушке индуктивности:

I_Leff = ,

Амплитуда напряжения на катушке индуктивности:

U_L = I_Leff ×X_L×1,41

Напряжение на элементе связи:

U_св = U_к× ,

где U_к амплитуда переменного напряжения на аноде лампы.

Эффективное значение тока через элемент связи:

I_свefft = 0,707×

2. Амплитудная модуляция

При заданной мощности в режиме несущей частоты Р_~н максимальнoе значениe напряжения на конденсаторе С₁ определяется формулой:

U_c1max = ,

а среднее за период низкой частоты эффективное значение тока через конденсатор С₁ равно:

I_c1efft = ,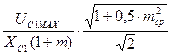

при m = 1 и m_ср = 0,3:

I_c1efft = 0,725 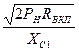= 0,362 ,

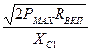где P_н и P_max - соответственно мощности в режиме несущей частоты и в максимальном режиме.

Максимальнoе напряжение на конденсаторе С₂ определяется формулой:

U_c2max = .

Эффективное значение тока через контурную катушку индуктивности в режиме несущей частоты при глубине модуляции m=1:

I_effн = = = = ,

откуда напряжение на контурной катушке индуктивности в максимальном режиме равно:

U_Lmax = 2.82×X_LI_effн = 2,82×X_L

Среднее за период низкой частоты эффективное значение тока через контурную катушку индуктивности определяется формулой:

I_Lefft = × ,

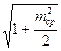при m_ср=0,3:

I_Lefft = 1.022

Напряжение на элементе связи в максимальном режиме при m = 1:

U_cвmax = 2U_кн ,

где U_кн - амплитуда переменного напряжения на аноде генераторной лампы в режиме несущей частоты.

При средней глубине модуляции m_ср = 0,3 среднее за период низкой частоты эффективное значение тока в элементе связи определяется формулой:

I_свfft = 0,725×

3. Усиление однополосного сигнала класса Н3Е.

Эффективное значение тока через катушку индуктивности П-контура, среднее за период низкой частоты, равно:

I_efft = 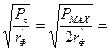0,707× 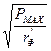= 0,5 ,

где Р_max и U_Lmax - соответственно пиковая мощность и пиковое значение напряжения на катушке индуктивности, а X_L - ее реактивное сопротивление. Тогда:

U_Lmax = 2×X_L×I_efft

Пиковые значения напряжений на емкостях П-контура определяются формулами: на входной емкости С₁:

U_c1ma =

на выходной емкости С₂:

U_c2max = ,

где R_вхфmax =W/K - наибольшее входное сопротивление антенного фидера.

Эффективные значения токов через конденсаторы П-контура, средние за период низкой частоты, рассчитывают по формулам:

I_cefft = 0,5U_cmax/X_C

Напряжение на элементе связи:

U_cвmax= X_cв,

где U_кmax - амплитуда переменного напряжения на аноде в пиковом режиме.

Эффективное значение тока через элемент связи, среднее за период низкой частоты, равно:

I_свefft =0,5 ,

где U_кmax - напряжение на контуре в пиковом режиме.

Программы PL-1AМ, PL-2AМ и PL-2SB

Эти программы, предназначенные для расчета описанных выше двухконтурных колебательных систем при индуктивной связи между контурами, отличаются от программ PLС-1AМ, PLС-2AМ и PLС-2SB тем, что содержат еще и расчет экстремального значения мощности второй гармоники рабочей частоты на входе антенного фидера, т.е. являются более полными (методика расчета фильтрации высших гармоник будет рассмотрена ниже в п.8.4).

Добротность П-контура, нагруженного волновым сопротивлением фидера W, определяется формулой

Q'_п = ,

где R_вх - входное сопротивление П-контура. Индекс "АМ" означает амплитудную модуляцию; "SB" - усиление однополосного сигнала класса Н3Е.

8.2.1.3. Описание алгоритма программ PLи PLС

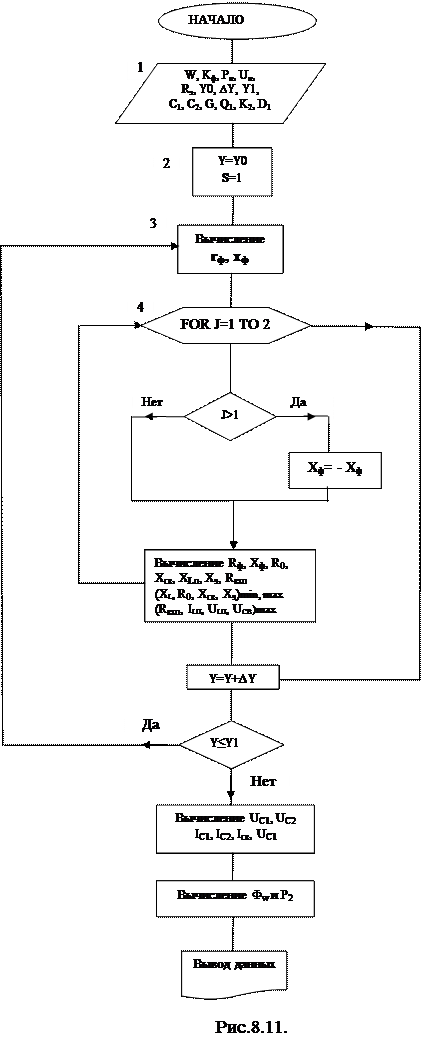
Алгоритм программы расчета двухконтурной ВКС приведен на рис.8.11. В качестве примера в Приложении 6.2 приведена программа PL1SB (на языке БЕЙСИК) и идентификация использованных в ней символов. Расчет производится для всех значений составляющих входного сопротивления антенного фидера с волновым сопротивлением W и КБВ К₁. В блоке «1» задаются исходные данные. Далее в цикле по Y при Y0 ≤ Y ≤ Y1 c шагом ΔY (блоки «2»-«9») рассчитываются значения элементов П-образного контура и элемента связи Х_св (в программе метки «13»-«30», «48»-«52»), максимальные и минимальные значения реактивных сопротивлений этих элементов, а также максимальные значения напряжений и токов в элементе связи и в П-контуре. (блок «10», в программе - метки «32»-«44»). Поскольку реактивная составляющая входного сопротивления фидера может иметь как знак «+», так и знак «–», то расчет величин элементов П–контура и элемента связи, а также значений напряжений и токов в контуре, производится во вложенном цикле по J: для J=1 и 2: при +jх_ф J=1, при –jx_ф J=2 (блоки «4»–«9», в программе – метки 15 – 45). В программах PL в блоке «11» (в программе – метки «57»-«79») рассчитывается экстремальное значение мощности второй гармоники на входе антенного фидера (см.п.8.4).

(блок «10», в программе - метки «32»-«44»). Поскольку реактивная составляющая входного сопротивления фидера может иметь как знак «+», так и знак «–», то расчет величин элементов П–контура и элемента связи, а также значений напряжений и токов в контуре, производится во вложенном цикле по J: для J=1 и 2: при +jх_ф J=1, при –jx_ф J=2 (блоки «4»–«9», в программе – метки 15 – 45). В программах PL в блоке «11» (в программе – метки «57»-«79») рассчитывается экстремальное значение мощности второй гармоники на входе антенного фидера (описание методики расчета см. п.8.4).

8.2.1.4. Расчет анодного контура

Вдвухконтурных ВКСанодный контур - простой параллельный (рис.8.12). Полную емкость контура С_к принимают ориентировочно равной С_апФ=(2÷4)λм.

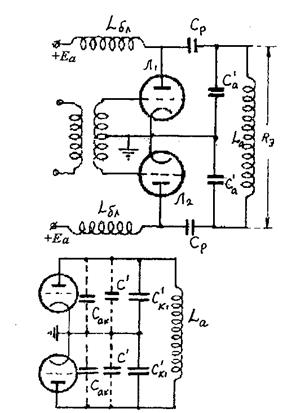
Рис.8.12

Эта емкость образована суммой емкостей контурного конденсатора С_к1 и cуммой выходной емкости генераторной лампы С_ак и емкости монтажа С^’.

Обычно принимают С_а=С_к1 + (1,5±2)С_ак. Таким образом, емкость контурного конденсатора равна С_к1=С_а – (1,5±2)С_ак. Модуль реактивного сопротивления этого конденсатора согласно (8.40) равен |X_Ск1|(Ом) = 532λ(м)/С_к1(пФ). Модуль реактивного сопротивления катушки индуктивности анодного контура |X_La| = |X_Cа| = r_a, где X_Cа – реактивное сопротивление емкостной ветви контура С_а. Значения емкости C_а и индуктивности L_a анодного контура определяются из (8.40).

Следует иметь в виду, что реактивное сопротивление Х_Э (8.39), трансформируемое при настройке колебательной системы элементом связи параллельно анодному контуру, должно быть скомпенсировано при настройке анодного контура. Од

нако, расчеты показывают, что как правило Х_Э >> r_a, поэтому при расчете анодного контура его влиянием можно пренебречь.

Эффективное значение тока в катушке индуктивности L_a определяется следующими формулами:

- при амплитудной модуляции:

I_Lefft = ,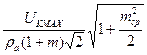

- при однополосной модуляции:

I_Lefft = 0,5×U_к /r_а,

Эффективное значение тока в контурном конденсаторе С_к1 равен:

- при амплитудной модуляции:

I_сefft = ,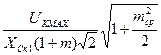

- при однополосной модуляции:

I_сefft = 0,5×U_к /Х_Ск1 ,

где U_к - амплитуда переменного напряжения на аноде лампы в пиковом режиме.

Добротность анодного контура равна:

Q_а=R_эr_а,

где R_э – эквивалентное сопротивление нагрузки лампы оконечного каскада.

Примечание.

При проектировании передатчиков, работающих в диапазоне волн λ_min÷ λ_ma,, расчет колебательной системы следует начинать при λ = λ_min

8.2.2. ВКС с настроенным на последовательный резонанс выходным П-образным контуром при максимуме КБВ на его входе

Программы PLK.

Эти программы предназначены для расчета элементов двухконтурной колебательной системы рис.8.10а, в которой выходной П-контур и элемент связи соединены в сечении 1-1 отрезком фидера с индикатором КБВ. Настройка колебательной системы производится при максимуме КБВ К₁ в соединительном фидере, при этом выходной П-контур настраивают на последовательный резонанс по обходу контура с учетом внесенного в контур входного сопротивления антенного фидера так же, как и в описанном выше методе настройки.

Если длина отрезка соединительного фидера с волновым сопротивлением W₁ пренебрежимо мала по сравнению с рабочей длиной волны передатчика, то можно считать, что на входе П-контура (рис.8.10б) КБВ К₁ равен:

К₁= , (8.41)

где р₁ - модуль коэффициента отражения - определяется формулой:

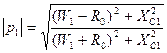(8.42)

Из (8.41) и (8.42) следует, что величина К₁ зависит от значений Х_с1 и R_о, которое определяется (8.32). С учетом (8.31) R_о можно представить формулой:

R₀= = ,

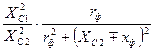откуда видно, что R_о зависит от соотношения емкостей П-контура N= и от входного сопротивления нагрузочного фидера. Зависимости К₁= f(N) имеют четко выраженный максимум, К_1max, положение которого зависит от соотношения емкостей П-контура N и от параметра а_2W . При заданном значении а_2W положение К_max зависит только от соотношения емкостей П-контура, т.е. от N= . Расчеты на ЭВМ показали, что при всех значениях входного сопротивления нагрузочного фидера W₁ максимумы КБВ К₁ всегда имеют место при одном и том же значении сопротивления R₀=W₁. Параметр а_2W влияет на положение К_1max, (т.е. на величину N, при котором имеет место К_1max) и на его величину, однако при К₁ = К_1max всегда R_о=W₁. Абсолютная величина К_max не влияет на напряжения и токи в колебательной системе. При настройке выходного П-контура по максимуму загрузки ламп оконечного каскада при К₁=К_1макс величина сопротивления элемента связи, а также напряжение и ток в нем, неизменны. Изменение параметра а_2W, т.е. емкости выходного конденсатора С₂ П-контура, влияет на напряжение и ток в его элементах и на напряжение на элементе связи. В качестве измерителя КБВ К₁ в соединительном фидере используется направленный ответвитель который устанавливают между катушкой связи и входом П-контура (в сечении 1-1 на рис.8.10б).

8.2.2.1. Расчет элементов колебательной системы

Программы PLK отличаются от программ PLС наличием в них подпрограммы, в которой при заданных значениях волнового сопротивления соединительного фидера W₁ и параметра a_2w П-контура определяется значение реактивного сопротивления его входной емкости С₁, при котором КБВ в соединительном фидере К₁ максимален. Расчет реактивных сопротивлений Х_L катушки индуктивности П-контура и Х_св элемента связи, а также напряжения и токи в элементах контурной системы производится по тем же формулам, что в программах PLС, но при R₀=W₁. Так, при усилении однотонового сигнала сопротивление элемента связи равно:

Х_св = Х_с1, (8.43)

Амплитуда переменного напряжения на элементе связи:

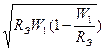U_св = U_к× , (8.44)

Эффективное значение тока через элемент связи:

I_свefft = 0,707× (8.45)

Амплитуда переменного напряжения на входной емкости С₁ П-контура:

U_c1max =U_{вх max} = , (8.46)

где R_вх – активная составляющая входной проводимости П-контура:

R_вх = 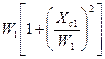. (8.47)

Трансформируемое элементом связи параллельно анодному контуру реактивное сопротивление Х_э, которое должно быть скомпенсировано при настройке анодного контура, равно:

= j 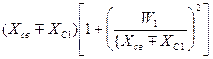, (8.48)

где верхний знак - при индуктивной связи между контурами, а нижний - при емкостной.

8.2.2.2. Настройка колебательной системы

Настройка колебательной системы производится следующим образом. Вначале задается величина параметра а_2w П-контура, а его емкости С₁ и С₂ устанавливают одинаковыми. При слабой связи между контурами (Х_св=Х_свmax) и при пониженном анодном напряжении настраивают в резонанс анодный контур (по минимуму анодного тока и максимуму сеточного тока генераторной лампы). Изменяя величину индуктивности L П-контура его настраивают на последовательный резонанс по максимуму выходной мощности (по фидерному индикатору мощности) и фиксируют величину КБВ К₁ в соединительном фидере. Затем подбирают величину сопротивления элемента связи, при которой режим ламп оконечного каскада оптимальный, при этом все время подстраивают анодный контур. Далее изменяют величину входной емкости С₁ П-контура (всякий раз настраивая его на последовательный резонанс) до получения КБВ К₁ = К_1max. В процессе настройки необходимо подстраивать анодный контур и восстанавливать рабочий режим ламп оконечного каскада. Если требуется снизить ток в элементах П-контура и напряжение на контурной катушке индуктивности L, следует уменьшить выходную емкость С₂, т.е. увеличить параметр а_2W, после чего повторить настройку. Окончательная регулировка колебательной системы производится при номинальном анодном напряжении.

8.2.2.3. Описание алгоритма программ PLK

Алгоритм программ PLK изображен на рис.8.13. В качестве примера в Приложении 6.3 приведена программа PLК2АМF (на языке БЕЙСИК) и идентификация использованных в ней символов. От программ PLС программы PLK отличаются наличием в них подпрограммы RAS (в алгоритме блоки «13» – «19», в программе – метки 67 –77), где определяется величина входной емкости С₁ П-контура, при которой КБВ К₁ на его входе максимален. В блоке «12» (в программе «47»-«60») производится расчет экстремального значения мощности второй гармоники на входе антенного фидера (см. п.8.4).

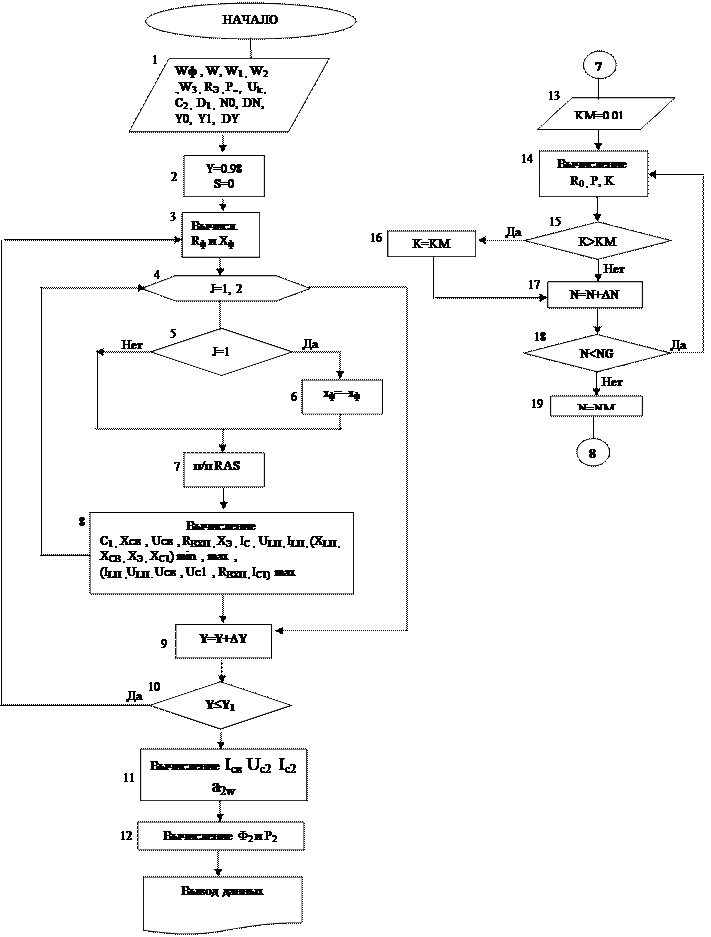
Рис.8.13.