Цифровые сигналы

Во всем мире сейчас активно развивается цифровая телефония. Качество цифровой телефонной связи значительно выше, чем обычной, поскольку цифровые сигналы меньше боятся всякого рода помех. Цифровой телефон позволяет предоставить нам массу дополнительных услуг. Появляется возможность к одной и той же телефонной линии подключить, казалось бы, внешне совершенно различные устройства – телефонный аппарат и персональный компьютер. Через цифровую телефонную сеть владельцам персональных компьютеров открывается доступ к банкам данных с широким ассортиментом информации.

В наши дома приходит цифровое кабельное телевидение, дающее необыкновенную четкость изображения и сочность красок; на прилавках магазинов мы можем увидеть аппаратуру цифровой звуко- и видеозаписи, обеспечивающую уникальное качество звука и изображения. Что же такое цифровой сигнал? Впервые мы столкнулись с ним, когда обсуждали факсимильный сигнал, полученный с черно-белого изображения, не содержащего полутонов.

Цифровыми сигналами являются телеграфные сигналы и сигналы передачи данных, вырабатываемые компьютерами. Таким образом, можно сказать, что цифровой сигнал – это последовательность импульсов. Если принять условно факт наличия импульса за 1, а факт его отсутствия за 0, то импульсную последовательность можно представить как чередование двух цифр: 0 и 1. Отсюда и появилось название «цифровой сигнал». Число, которое принимает только два значения: 0 и 1, называется «двоичной цифрой». В переводе на английский это звучит как «binary digit». В практику широко вошло сокращение, составленное из начальных и конечных букв английского словосочетания, т.е. слово «bit», что на английском читается как бит. Итак, одна позиция в цифровом сигнале есть 1 бит; это может быть либо 0, либо 1. Восемь позиций в цифровом сигнале объединяется понятием байт. При передаче цифровых сигналов естественным образом вводится понятие скорости передачи – это количество бит, передаваемых в единицу времени, чаще всего, в секунду.

Дискретизация аналоговых сигналов

По своей природе многие сигналы (телефонные, факсимильные, телевизионные) не являются цифровыми. Это аналоговые, или непрерывные, сигналы. Можно ли «переложить» живую человеческую речь на язык нулей и единиц, сохранив при этом все богатое разнообразие красок человеческого голоса, всю гамму человеческих эмоций? Другими словами, речь идет о том, как заменить непрерывный процесс последовательностью цифр, не потеряв при этом информации о непрерывном процессе.

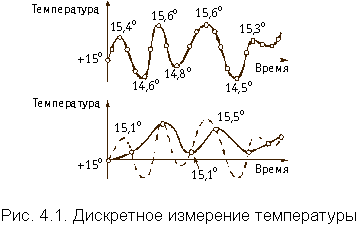
С подобной проблемой мы сталкиваемся в жизни довольно часто. Если через очень короткие промежутки времени (скажем, через 1с) наносить значения температуры воздуха на график, то получим множество точек, отражающих изменение температуры (рис. 4.1). Таким образом, имеем дело не с непрерывной кривой изменения температуры, а лишь с ее значениями, отсчитанными через определенные промежутки времени. По сути говоря, мы описали некоторый непрерывный процесс последовательностью десятичных цифр. Подобный процесс называется дискретизацией непрерывного сигнала. Невыясненным остался вопрос, как часто следует брать отсчетные значения непрерывной кривой, чтобы отследить все ее изменения. Так, при более длительных промежутках времени между наблюдениями за температурой воздуха не удается отследить все ее быстрые изменения.

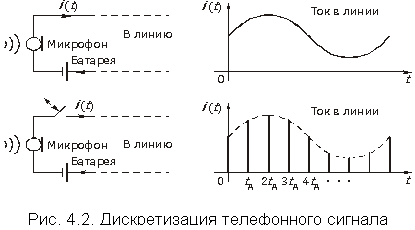
Аналогичный подход лежит в процессе дискретизации телефонного сигнала. Если в цепь микрофона (рис. 4.2), где ток является непрерывной функцией времени, встроить электронный ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала, и представлять собой ничто иное, как дискретный сигнал (см. рис. 4.2). Интервал времени 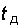через который отсчитываются значения непрерывного сигнала, называется интервалом дискретизации. Обратная величина 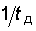(обозначим ее 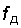) называется частотой взятия отсчетов, или частотой дискретизации.

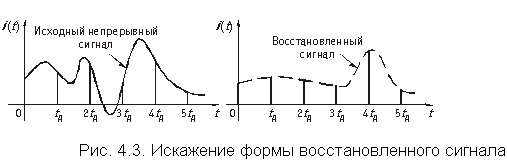
Отсчеты непрерывного сигнала, так же, как и отсчеты температуры, следует брать с такой частотой (или через такой интервал времени), чтобы успевать отследить все, даже самые быстрые, изменения сигнала. Иначе при восстановлении этого сигнала по дискретным отсчетам часть информации будет потеряна и форма восстановленного сигнала будет отличаться от формы исходного (рис. 4.3). Это означает, что звук на приеме будет восприниматься с искажениями. Чтобы разобраться с этим вопросом, начнем с колебания струны. Вы тронули струну, она стала вибрировать и своим движением то сжимать, то разряжать окружающий воздух или, другими словами, то повышать, то понижать его давление. Слои воздуха повышенного и пониженного давления начали разбегаться во все стороны от колеблющегося тела. Образовалась звуковая волна. Нечто похожее наблюдаем, когда бросаем камни в воду и смотрим на расходящиеся кругами волны. Гребни этих волн можно сравнить с областью сжатого воздуха, впадины – с областью разреженного воздуха. Давление звуковой волны, распространяющейся от струны, изменяется во времени по закону синусоиды. Чтобы отследить все ее изменения, очевидно, достаточно брать отсчетные значения в моменты, соответствующие максимумам и минимумам синусоиды т.е. с частотой, превышающей по крайней мере вдвое частоту звукового колебания. Например, если струна совершает 20 колебаний/с (частота 20 Гц), то максимальное звуковое давление будет наблюдаться через каждый 1/20 с, т.е. через 50 мс. Максимумы и минимумы кривой звукового давления разделены интервалами в 25 мс. Значит, отсчетные значения по кривой должны следовать не реже, чем через 25 мс, или с частотой 40 отсчетов/c (40 Гц). Обычно отсчетные значения на кривой берут «с запасом»: не в 2 раза чаще, чем колеблется звук, а, скажем, в 10 раз. В этом случае они очень хорошо передают форму кривой. Интересен случай, когда звуковые волны излучают две одновременно колеблющиеся струны. На рис. 4.4 показаны три варианта: вторая струна колеблется в 2, 3 и 10 раз чаще, чем первая. Давления двух звуковых волн на пластину, помещенную на их пути, складываются. График результирующего давления уже не является синусоидой. Мы видим, что быстрые изменения в этой кривой обусловлены более высокочастотным колебанием (в данном случае колебанием второй струны). Для того чтобы отследить все быстрые изменения результирующего звукового давления, отсчетные значения следует брать с частотой, по крайней мере вдвое превышающей частоту колебания второй струны. В последнем варианте частота взятия отсчетных значений должна превышать 400 Гц. Это означает, что отсчетные значения должны следовать не реже, чем через 1/400 = 0,0025 c = 2,5 мс, а лучше – еще чаще, например через 0,5 мс. При изучении речи мы выяснили, что голосовые связки у человека играют роль струн. Самое высокочастотное колебание этих «струн», которое по рекомендации МСЭ необходимо еще учитывать, имеет частоту 3400 Гц. При переходе от аналогового речевого сигнала к цифровому это значение обычно округляют до4000 Гц. Это значит, что при замене непрерывной кривой электрического тока на выходе микрофона телефонного аппарата отсчетными значениями последние необходимо брать с частотой 8000 Гц или, другими словами, не реже, чем через 1/8000 = 0,000125 c = 125 мкс.

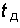Чтобы восстановить исходный сигнал из дискретного, достаточно пропустить дискретный сигнал через фильтр нижних частот с граничной частотой полосы пропускания F и подавить все «боковые» спектры. На выходе такого фильтра появится исходный непрерывный сигнал. При слишком редкой дискретизации (низкая частота дискретизации и большой интервал дискретизации ) будет иметь место наложение на спектр исходного сигнала «бокового» спектра. Это приведет к искажению формы исходного спектра, и значит, к отличию восстановленного сигнала от исходного. Наоборот, более частая дискретизация позволит легко восстановить непрерывный сигнал из дискретного с помощью несложного фильтра нижних частот. Таким образом, для безыскаженного восстановления непрерывного сигнала из дискретного необходимо частоту дискретизации 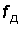выбирать не ниже удвоенной ширины его спектра. Для телефонного сигнала, как мы это видим, 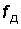= = 8 кГц.В 1933 году в работе «О пропускной способности «эфира» и проволоки в электросвязи» В.А. Котельников доказал теорему, ставшую основополагающей в теории и технике цифровой связи. Суть этой теоремы состоит в том, что непрерывный сигнал, у которого спектр ограничен частотой F, может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым с частотой 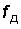= 2F, т.е. через интервалы времени 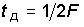. Мы не приводим полную математическую формулировку теоремы, а также ее доказательство, а лишь ограничиваемся указанием сути теоремы.

Квантование

Пусть в результате дискретизации непрерывного сигнала s(t) была получена последовательность узких импульсов, которая представляет собой АИМ-сигнал. Амплитуды импульсов равны в этом случае мгновенным значениям сигнала s(t) в моменты 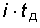, где i = 0, 1, 2, 3, ...; 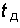– период следования импульсов, или интервал дискретизации.

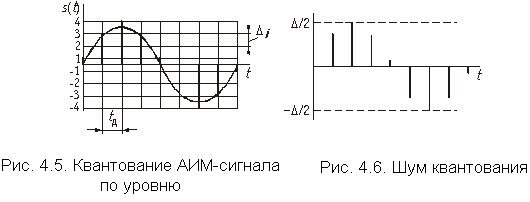
Подвергнем полученный АИМ-сигнал квантованию по уровню (рис. 4.5). Для этого диапазон возможных значений амплитуд (т.е. диапазон значений первичного сигнала) делится на отрезки, называемые шагами квантования 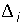. Границы этих отрезков являются разрешенными для передачи значений амплитуд импульсов. Таким образом, амплитуды передаваемых импульсов будут равны не мгновенным значениям первичного сигнала, а ближайшим разрешенным уровням. Такое преобразование первичных сигналов можно называть квантованной амплитудно-импульсной модуляцией (КАИМ). Особенностью КАИМ-сигнала является то, что все его уровни можно пронумеровать (а их число хотя и большое, но конечное) и тем самым свести передачу КАИМ-сигнала к передаче последовательностей номеров уровней, которые этот сигнал принимает в моменты 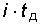. Если шаги квантования одинаковы и не зависят от уровня квантования, то квантование называют равномерным. Возможно неравномерное квантование, при котором шаги квантования различны. В процессе квантования возникает ошибка вследствие того, что передаваемый квантованный сигнал отличается от истинного. Эту ошибку можно рассматривать как специфическую помеху – шум квантования. Последний представляет собой случайную последовательность импульсов (рис. 4.6), максимальное значение амплитуды которых не превышает половины шага квантования. Чем меньше шаг квантования, тем меньше шум, но больше число передаваемых разрешенных уровней. Следующий шаг в преобразовании сигнала состоит в переводе квантованного АИМ-сигнала в цифровой. Эта операция называется кодированием КАИМ-сигнала.

Кодирование

Познакомимся с одним замечательным свойством нашей системы счисления – позиционностью. Изобразим какое-нибудь число, например 777. В нем один и тот же знак «7» участвует 3 раза, но когда он стоит справа, то означает семь единиц, в центре – семь десятков, слева – семь сотен. Таким образом, при записи числа цифра может иметь начертание одно и то же, а цифровые значения – разные, в зависимости от места, позиции, разряда, на котором она стоит. Такой принцип построения чисел называется поместным, или позиционным. Для записи любых сколь угодно больших чисел достаточно десяти цифр! Каждая позиция, или разряд, числа имеет определенный «вес» (единицы, десятки, сотни и т.д.), поэтому число 777 можно расписать как

777 = 7 ? 10² + 7 ? 10 + 7,

т.е. как семь сотен плюс семь десятков плюс семь единиц. Если призвать на помощь алгебру и вместо чисел записать буквы, то можно получить такую общую форму представления числа: 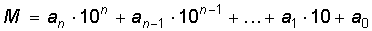или сокращенную – через коэффициенты, если опускать степени числа 10: .

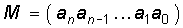Число 10 является основанием системы счисления. Коэффициенты 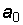(число единиц), 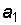(число единиц второго разряда, т.е. десятков), 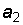(число единиц третьего разряда, т.е. сотен) и т.д. могут принимать значения, не превышающие основания системы: от 0 до 9. В 1665 г. французский математик Б. Паскаль показал, что за основание системы счисления можно принять любое число, а это значит, что каждое число можно представить в виде комбинации степеней не числа 10, какого-либо другого целого числа. Выберем, например, число 7:

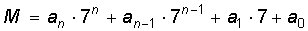
Ясно, что значения коэффициентов 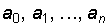должны теперь быть не больше нового основания, т.е. 7: они могут принимать значения от 0 до 6. Представим число 777 в семеричной системе, разлагая его по степеням основания 7: .

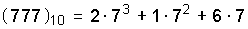Если опустить степени числа 7, как мы делаем при записи чисел в десятичной системе, то получим семеричную запись этого числа: (2160)7. Здесь цифра 7 в индексе указывает основание системы. В пятеричной позиционной системе всего пять цифр: 0, 1, 2, 3, 4. В ней число 777 будет представляться количеством «пятерок», «двадцатипяток» и т.д.: .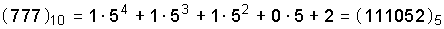

Посмотрим, как будет представлено число 777 в двенадцатеричной системе. Поскольку в ней должно быть двенадцать цифр, а мы знаем только десять, то придется ввести еще две цифры, обозначив 10, скажем, буквой A, а 11 – буквой B. В результате получим .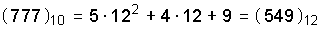

Как видите, можно придумать много различных позиционных систем счисления, отличающихся только основаниями. И все они, вообще говоря, равнозначны: ни одна из них не имеет явных преимуществ перед другой!Число 2 – это самое меньшее из чисел, которое можно взять за основание системы счисления. Поэтому в двоичной системе счисления всего две цифры: 0 и 1. Число в двоичной системе запишется так: .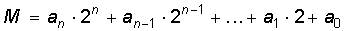

Если в десятичной системе «вес» каждой позиции (или разряда) числа равен числу 10 в некоторой степени, то в двоичной системе вместо числа 10 используют число 2. «Веса» первых 13 позиций (разрядов) двоичного числа имеют следующие значения:

Попробуем записать уже привычное нам число (777)10 в двоичной системе счисления, представляя его в виде разложения по степеням двойки и отбрасывая потом при записи сами степени: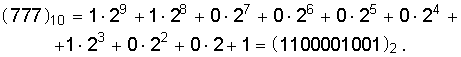

Итак, в двоичной системе счисления вместо числа 777 приходится писать число 1100001001.При записи числа в двоичной системе каждая позиция занята двоичной цифрой. Вместо двух слов «двоичная цифра» употребляют одно слово: «бит». Мы уже упоминали, что оно произошло от английского «bit», составленного из начальных и конечной букв словосочетания «binary digit», что в переводе с английского означает «двоичная цифра». С помощью одного бита можно записать только число 0 и 1, двух бит – числа от 0 до 3, трех бит – числа от 0 до 7, четырех бит – числа от 0 до 15 и т.д.

Чтобы записать числа от 0 до 1 000, потребуется десять бит. В двоичной системе счисления даже сравнительно небольшое число занимает много позиций. Как теперь перевести дискретные значения тока микрофона в цифровой двоичный код? В XVIII веке крупнейший математик Л. Эйлер показал, что с помощью набора гирь 1, 2, 4, 8, и 16 кг можно взвесить любой груз с точностью до 1 кг. Взвешиваемый груз (обозначим его массу через М, кг) математически можно представить как

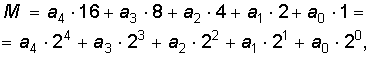где каждый коэффициент a = 1, если соответствующую гирю кладем на чашу весов, a = 0, если этой гирей не пользуемся при взвешивании. Таким образом, процедура взвешивания сводится к представлению десятичного числа в двоичной системе счисления. Поясним это на примере. Пусть нам нужно взвесить груз массой 21 кг. Поставим сначала на чашу весов самую большую гирю – массой 16 кг. Поскольку она не перетягивает груз, оставим гирю на чаше ( 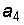= 1) и добавим следующую – 8 кг. Ясно, что в этом случае чаша весов с гирями перетянет чашу с грузом. Снимем эту гирю ( 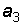= 0) и установим гирю массой 4 кг. Проведя взвешивание до конца, мы увидим, что на весах остались гири массой 16, 4 и 1 кг. Значения коэффициентов дают пятиразрядный двоичный код 10101 числа 21. Механический груз мы взвешивали на механических весах. Считая отсчетное значение тока, появляющееся на выходе электронного ключа, своего рода «электрическим грузом», можно осуществить аналогичное взвешивание, но на этот раз электронным способом. Такие «электронные весы» назвали кодером (от английского соder – кодировщик). Допустим, отсчетное значение тока равно 21 мА. Роль «электрических гирь» в кодере выполняют эталонные токи величиной 16, 8, 4, 2 и 1 мА, которые вырабатываются специальным устройством. Каждая проба – подходит та или иная «гиря» либо нет – производится в строго установленные промежутки времени. Вся процедура взвешивания должна закончиться до прихода с электрического ключа следующего отсчетного значения тока (напомним, для звуков речи это время составляет всего 125 мкс). Итак, сначала отсчетное значение тока сравнивается с эталоном, равным 16 мА, и, поскольку оно больше эталона, на выходе кодера появляется импульс тока, что соответствует двоичной цифре 1. В следующий интервал времени к первому эталонному току добавляется второй величиной 8 мА. Теперь суммарный вес «электрической гири» равен 24 мА. Это больше отсчетного значения, поэтому второй эталонный генератор отключается. На данном интервале времени импульс тока на выходе кодера не появляется, что соответствует двоичной цифре 0. Думаем, читатели без труда завершат процедуру взвешивания. Таким образом, за время взвешивания одного отсчетного значения кодер вырабатывает серию импульсов, полностью повторяющую двоичный код отсчетного значения микрофонного тока. Нельзя не напомнить вновь еще об одном виде искажений, появляющихся при переводе отсчетного значения тока в двоичный код. Так, если кодированию подвергается отсчетное значение 21,7 мА, кодер все равно выдает код 10101, как и в случае целого значения 21 мА. Это и понятно, поскольку «взвешивание» проводилось с точностью до 1 мА – веса самой меньшей «электрической гири». Такое округление чисел в технике называется квантованием, а разница между отсчетным значением тока и величиной, набираемой двоичным кодом, – ошибкой квантования. Однако и искажения, вызванные ошибками квантования, можно если и не исключить совсем, то по крайней мере значительно уменьшить. Пусть, например, самая маленькая «электрическая гиря» будет иметь «вес» 0,125 мА. Тогда, взяв восемь «гирь», соответствующие 16; 8; 4; 2; 1; 0,5; 0,25; 0,125 мА, можно будет «взвешивать» отсчетные значения тока с точностью до 0,125 мА. При этом число 21 представится 8-разрядным двоичным кодом 10101000, а число 21,7 – кодом 10101101, где последние три цифры означают добавку 0,625 к числу 21. Применение же 12-разрядного двоичного кода позволяет вместо числа 21,7 набрать весьма близкое к нему число 21,6921895. Успехи в развитии интегральной микросхемотехники позволили объединить в корпусе одной небольшой микросхемы электронный ключ и кодер. Эта микросхема преобразует непрерывную (часто говорят аналоговую) электрическую величину в двоичный цифровой код и известна под названием аналого-цифрового преобразователя (АЦП). Выпускаются АЦП с 8-, 10- и 12-разрядными двоичными кодами. Интересно подсчитать, какую скорость имеет цифровой поток, полученный из непрерывного телефонного сигнала путем дискретизации его через 125 мкс и 8-разрядного кодирования. За секунду ток микрофона изменяется 8000 раз. В 8-разрядном кодере каждое измеренное значение тока представляется двоичным словом из 8 бит. Значит, каждую секунду в линию отправляется 8000 ? 8 = 64000 бит, т.е. скорость цифрового потока равна 64 кбит/сек.

Кодовая комбинация из 8 бит, образующая двоичное слово, называется байтом. Символы в каждой кодовой комбинации отделены друг от друга временным интервалом tт, т.е. следует с частотой 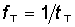. Эта частота называется тактовой. Преобразование отсчетов непрерывного сигнала в двоичный код называется импульсно-кодовой модуляцией (ИКМ). В настоящее время этот способ получения цифровых сигналов из аналоговых наиболее распространен. Системы передачи, использующие данное преобразование сигналов, называются ИКМ системами. В иностранной литературе используется аббревиатура РСМ (от английских слов pulse code modulation, что в переводе как раз и означает импульсно-кодовая модуляция).

Восстановление аналоговых сигналов

Все устройства, предназначенные для демодуляции сигналов, будут рассмотрены при изучении конкретных систем передачи и аппаратуры, входящей в состав этих систем. При приеме сигналов ИКМ для восстановления аналогового сигнала необходимо преобразовать цифровой сигнал (последовательность двоичных импульсов) в квантованный АИМ сигнал (такое преобразование называется декодированием) и затем осуществить операцию демодуляции, т.е. выделения из АИМ-сигнала аналогового сигнала s(t). Итак, при использовании ИКМ выполняются следующие преобразования аналогового сигнала: в пункте передачи – амплитудно-импульсная модуляция, квантование и кодирование; в пункте приема – декодирование и демодуляция квантованного АИМ сигнала. Полученный на приеме аналоговый сигнал отличается от переданного, так как образуется из квантованных импульсов, амплитуды которых равны не мгновенным значениям сигнала s(t), а ближайшим разрешенным значениям. Таким образом, операция квантования вносит в процесс передачи сигнала неустранимую ошибку, которая тем меньше, чем больше уровней квантования. А как узнать, какое десятичное число скрывается под его записью в двоичной системе? Правило простое: под каждым разрядом двоичного числа следует записать его «вес». Те «веса», которые соответствуют единичным разрядам, нужно сложить. Полученная сумма и явится десятичным числом. Вот перед нами число 1001011, записанное в двоичной нумерации. Поступаем согласно сказанному выше:

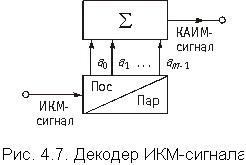
Как видим, заинтересовавшее нас число складывается из единицы, двойки, восьмерки и шестидесяти четырех (1 + 2 + 8 + 64). Очевидно, оно равно 75. Попробуйте самостоятельно определить, какому числу соответствует его двоичная запись 10110011. В состав декодера входит преобразователь последовательного кода в параллельный (рис. 4.7), на выходах которого появляется набор единиц и нулей, соответствующий принятой кодовой комбинации. Каждая единица (токовый импульс) поступает на вход сумматора с весом, где увеличивается в 2^k раз. На выходе сумматора возникает импульс, амплитуда которого определяется кодовой комбинацией на входе декодера. Например, при прохождении кодовой комбинации 0100110 на первый, четвертый, пятый и седьмой входы сумматора напряжение не подается (бестоковые импульсы), а на второй, третий и шестой входы подается напряжение, которое увеличивается соответственно в 2¹, 2² и 2⁵ раз. На выходе сумматора появляется напряжение, пропорциональное 2¹ + 2² + 2⁵ = 38, т.е. квантованный АИМ-сигнал. На следующем шаге необходимо из отсчетных значений тока получить непрерывный ток. Сделать это нам поможет обычный конденсатор небольшой емкости, который при кратковременном воздействии на него тока (т.е. отсчетного значения) мгновенно зарядится и будет удерживать заряд до следующего кратковременного воздействия. Отметим еще раз, что восстановленная таким путем кривая непрерывного тока будет несколько отличаться от той, которая была получена на клеммах микрофона: она будет иметь плоские ступеньки между отсчетными значениями. Можно сказать, что процесс взятия отсчетных значений и последующего восстановления непрерывной кривой тока микрофона сопровождается специфическими искажениями, которые могут повлиять на качество воспроизведения звука. Однако на практике для восстановления тока используют не конденсатор, а более сложные схемы, делающие форму восстановленного тока похожей на форму исходного тока и тем самым сводящие на нет действия указанных искажений.

Контрольные вопросы

1. Что такое цифровой сигнал? 2. С какой частотой следует дискретизировать аналоговый сигнал? 3. Как определить ошибку квантования сигнала? 4. В чем заключается принцип двоичного кодирования сигнала? 5. Как восстановить аналоговый сигнал из цифрового?

Список литературы

1. Крук Б.И., Попов Г.Н. ... И мир загадочный за занавесом цифр: Цифровая связь. – 2-е изд., испр. – Новосибирск: ЦЭРИС, 2001. – 264 с. 2. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебник для вузов; Под ред. В.П. Бакалова. – М.: Радио и связь, 2000. – 592 с. 3. Журавлева О.Б., Крук Б.И. Дискретные сигналы и цепи: 26 вопросов и ответов: Учебное пособие для дистанционного обучения. – Новосибирск: СибГУТИ, 1999. – 100 с.