Обозначим в уравнениях передачи (13.8) Uп = (U1 + I1Zв)/2 и U0 = (U1 – I1Zв)/2. С учетом этих обозначений запись уравнений передачи однородной длинной линии упростится и будет иметь вид
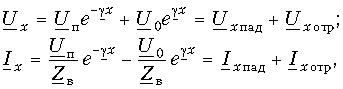
где
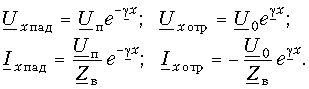
Напряжение и ток состоят из сумм двух слагаемых. Первые слагаемые уменьшаются с увеличением расстояния от начала линии х, вторые – возрастают. Создается впечатление о существовании в линии двух типов волн: падающей и отраженной. Чтобы убедиться в этом, рассмотрим мгновенные значения напряжения и тока.
Помня, что в (13.10) все величины в общем случае комплексные
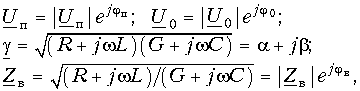
можно по известным правилам перейти от (13.10) для комплексных значений к уравнениям передачи для мгновенных значений напряжений и токов. Для простоты положим jп = j0 = 0. Тогда
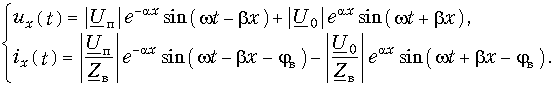
Проанализируем сначала первые слагаемые этих уравнений, которые обозначим
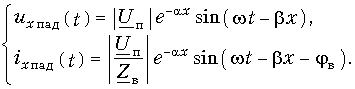
В каждом сечении линии (т. е. в каждой точке х) колебания напряжения и тока являются гармоническими. Амплитуда этих колебаний уменьшается по мере удаления от начала линии по закону е–aх. В каждой последующей точке линии колебания отстают по фазе от колебаний в предыдущей точке (на это указывает знак «минус» перед bх).
Если в момент времени t1 сделать фотографию распределения, например, напряжения uxпад вдоль линии, то она будет иметь вид кривой 1 (рис. 13.3). В следующий момент t2 фаза напряжения в каждой точке линии изменится на величину w(t2 – t1), и вся картина как бы сместится вдоль оси х вправо (кривая 2 на рис. 13.3). Аналогичная ситуация будет наблюдаться и в момент времени t3 > t2 (кривая 3 на рис. 13.3).
Если сделать последовательно ряд мгновенных фотографий и затем их проецировать на экран, то создается впечатление движущейся волны напряжения вдоль цепи. Фактически же вдоль цепи распространяется состояние равной фазы. Например, можно взять точку цепи х1, соответствующую максимуму напряжения в момент времени t1 (точка А на рис. 13.3) и определить скорость ее перемещения. Скорость распространения вдоль цепи состояния равной фазы называется фазовой скоростью распространения
В момент времени t1 в точке х1 имеется определенное фазовое состояние wt1 – bх1. Это же фазовое состояние будет наблюдаться в точке х2, но уже в момент времени t2 wt2 – bх2. Приравнивая их получаем wt1– bх1= wt2– bх2
Фазовую скорость распространения (км/с) найдем как отношение расстояния х2– х1, пройденного точкой A, ко времени t2 – t1
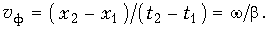
Таким образом, уравнения (13.12) описывают волны напряжения и тока, распространяющиеся от начала к концу линии. Такие волны называются падающими
Обратимся ко вторым слагаемым выражений (13.11), которые обозначим
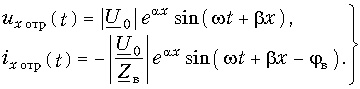
Эти слагаемые описывают волны точно такого же характера, как и падающие, но распространяющиеся в обратном направлении, т. е. от конца линии к началу. Эти волны называются отраженными волнами напряжения и тока. Амплитуды отраженных волн убывают от конца линии к началу, наибольшая амплитуда наблюдается в конце линии.
В соответствии с рассмотренной картиной можно сказать, что в установившемся режиме гармонических колебаний напряжение и ток в любой точке линии складываются из падающих и отраженных волн напряжения и тока, т. е. ux = uxпад + uxотр; ix = ixпад + + ixотр. Отраженные волны возникают в конце линии.
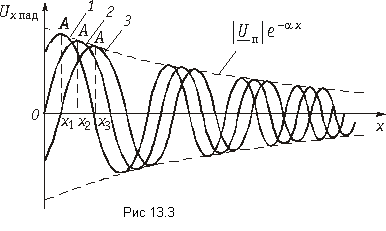
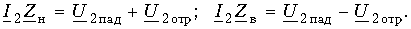
Складывая эти равенства и вычитая из первого второе, имеем:
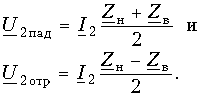
Отношение комплексной амплитуды отраженной волны к комплексной амплитуде падающей волны называется коэффициентом отражения по напряжению
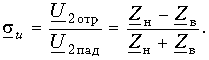
Отсюда
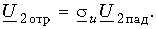
Коэффициент отражения по напряжению показывает, какую часть амплитуды падающей волны в конце линии составляет амплитуда отраженной волны. Амплитуда отраженной волны тока
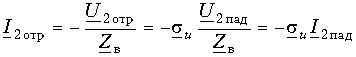
В то же время I2отр = siI2пад, где si – коэффициент отражения по току. Отсюда видно, что si = —su, т. е. коэффициент отражения по току равен по значению и противоположен по знаку коэффициенту отражения по напряжению.
Рассмотрим некоторые частные режимы работы линии. Если линия замкнута накоротко на конце (короткое замыкание (КЗ)), т. е. Zн = 0, то коэффициент su= —1, а коэффициент si= 1. Падающая и отраженная волны напряжения в конце линии имеют равные амплитуды и сдвинуты по отношению друг к другу на 180°. Амплитуда результирующей волны напряжения в конце линии будет равна нулю. В то же время падающая и отраженная волны тока будут иметь равные амплитуды, что приведет к увеличению тока в конце короткозамкнутой линии.
При холостом ходе (XX) в конце линии Zн = ¥ коэффициент su = 1 и si=—1, т. е. картина изменится на противоположную: ток в нагрузке будет равен нулю, а напряжение увеличится вдвое. Случай, когда Zн = Zв, рассмотрен ниже.

