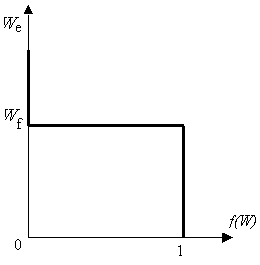Само название “полупроводник” произошло от различия электропроводности полупроводников от электропроводности металлов и диэлектриков.

Действительно, . Но этот признак не является решающим в классификации.

Основными свойствами, отличающими полупроводники от других твердых тел, являются следующие:

1. Характер и величина зависимости электропроводности от температуры. Проводимость полупроводников возрастает с увеличением температуры по экспоненциальному закону 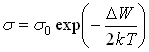( 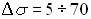на 1° Кельвин). У металлов увеличение температуры приводит к уменьшению проводимости.
2. Сильное влияние примеси на проводимость. Что значит сильнее? Концентрация примеси 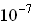, 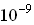% уже существенно увеличивает проводимость. У металлов же введение примеси уменьшает проводимость. Почему?
3. Высокая чувствительность электрических свойств полупроводников ко всякого рода внешним воздействиям (механическая деформация, облучение светом, рентгеновскими лучами или быстрыми частицами и др.).

В электронике находят применение ограниченное число полупроводников. Это германий, кремний, арсенид галия, антимонид индия и др.

1. Кристаллическая структура полупроводников и зонная теория

1. Применяемые в технике полупроводники имеют весьма совершенную кристаллическую структуру – атомы размещены в пространстве на постоянных расстояниях, образуя кристаллическую решетку. Такие полупроводники, как германий и кремний имеют структуру типа алмаза, в которой каждый атом окружен такими же атомами, находящимися в вершинах правильного тетраэдра. Плотность размещения атомов для германия 4,45·10²² 1/см³, для кремния – 5·10²² см ^-3.

Каждый атом в кристаллической решетке или электрически нейтрален и связан ковалентными (парно–электронными) связями с четырьмя равно–отстоящими от него соседними атомами. В полупроводниках типа ионно–ковалентная связь. Валентные электроны распределяются между соседними атомами. В результате каждый атом окружен стабильной группой из восьми электронов связи.

2. Если не нужно выделять кристаллографического направления, такую решетку изображают на плоскости (рисунок 1.1).

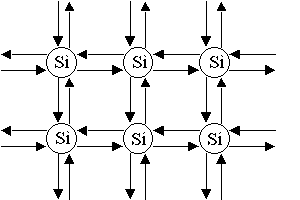
Рисунок 1.1- Кристаллическая решетка , изображенная на плоскости

Это идеальная решетка. При все узлы заняты, все связи заполнены. Свободных носителей заряда нет.

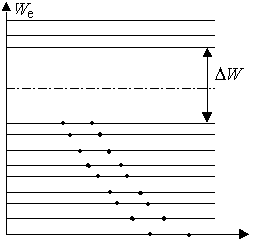
3. С точки зрения зонной теории твердого тела, такой кристалл изображается энергетической диаграммой, представленной на рисунке 1.2.

Заполнение энергетических уровней электронами подчиняется статистике Ферми–Дирака, в основе которой лежат следующие положения:

1. все электроны тождественны;
2. выполняется принцип Паули;
3. функция распределения 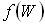, т. е. вероятность заполнения уровня с энергией W имеет следующий вид: 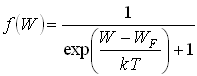где 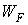– энергия Ферми, смысл–уровень энергии, вероятность заполнения которого равна .

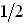По определению функция распределения есть отношение числа частиц с энергией в интервале от W до W+dW к числу возможных состояний в этом же интервале энергий N(W), т. е.

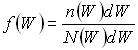
При (обычный случай для полупроводников, используемых для приборов) единицей в знаменателе функции распределения Ферми–Дирака можно пренебречь, и функция принимает вид

Зная функцию распределения и можно определить число частиц с определенной энергией :

где k – постоянная Больцмана.

При T=0 (рисунок 1.3) валентная зона полностью заполнена f(W)=1 (это электроны, участвующие в ковалентных связях); зона проводимости пустая f(W)=0 (свободных носителей заряда нет), ΔW– ширина запрещенной зоны. Уровень Ферми расположен строго посередине запрещенной зоны.