Для определенности положим, что f(t) имеет смысл тока i(t). Тогда действующее значение периодического негармонического тока определяется согласно (3.5), где i(t) определяется уравнением (5.10): 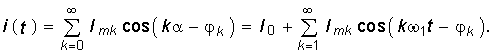(5.17)

Подставив это значение тока в (3.5), после интегрирования получим 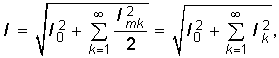(5.18)

т. е. действующее значение периодического негармонического тока I полностью определяется действующими значениями его гармоник I_k и не зависит от их начальных фаз _k.

Аналогичным образом находим действующее значение периодического несинусоидального напряжения: 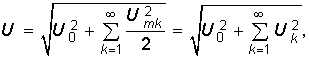(5.19)

Среднее значение тока определяется согласно общему выражению (3.9). Причем обычно берут среднее значение i(t) по абсолютной величине 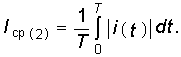(5.20)

Аналогично определяется U_ср(2).

С точки зрения теории цепей, большой интерес представляет средняя активная мощность негармонического сигнала и распределение ее между отдельными гармониками.

Средняя активная мощность периодического несинусоидального сигнала 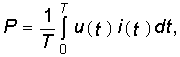(5.21) где 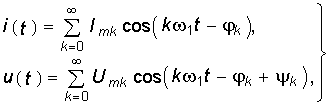(5.22)

_k — фазовый сдвиг между током и напряжением k-й гармоники.

Подставляя значения i(t) и u(t) из (5.22) в уравнение (5.21), после интегрирования получаем: 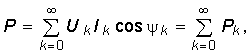(5.23) т, е. средняя за период активная мощность периодического негармонического сигнала равна сумме мощностей отдельных гармоник. Формула (5.23) является одной из форм широко известного равенства Парсеваля.

Аналогично находим реактивную мощность 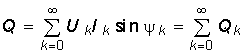(5.24) и полную мощность 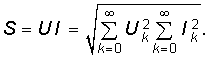(5.25)

Следует подчеркнуть, что в отличие от гармонических сигналов для негармонических сигналов (5.26)

Величина P_иcк = носит название мощности искажений и характеризует степень различия в формах тока i(t) и напряжения u(t).

Кроме мощности искажений периодические негармонические сигналы характеризуются еще рядом коэффициентов: мощности, k_м = P/S; формы K_ф = U/U_ср(2); амплитуды K_a = U_m/U; искажений k_и = U₁/U; гармоник k_г = 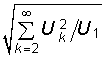и др.

Для синусоидального сигнала k_ф = /21,11; k_a = 1,41; k_и = 1; k_г = 0.