Сигнал – это физический процесс (например, изменяющиеся во времени токи и напряжения), содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией.
Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией ![]() , которая может принимать любые значения в определенном интервале; дискретные сигналы
, которая может принимать любые значения в определенном интервале; дискретные сигналы ![]() представляют собой последовательности или отсчеты функции
представляют собой последовательности или отсчеты функции ![]() , взятые в определенные дискретные моменты времени nT; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами.
, взятые в определенные дискретные моменты времени nT; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами.
Если в цепь микрофона (рис. 1), где ток ![]() является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.
является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.
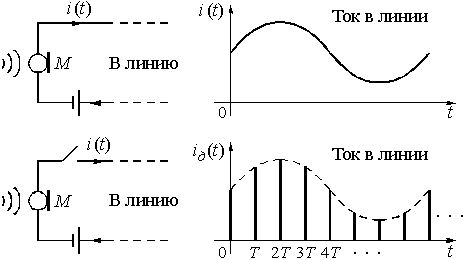
Рис. 1
В отличие от непрерывного сигнала ![]() дискретный сигнал можно обозначить
дискретный сигнал можно обозначить ![]() . Однако, чаще его обозначают
. Однако, чаще его обозначают ![]() , заменяя непрерывное время t дискретными моментами nT, следующими строго через интервал T. Используются и более краткие обозначения:
, заменяя непрерывное время t дискретными моментами nT, следующими строго через интервал T. Используются и более краткие обозначения: ![]() и
и ![]() . Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n < 0 дискретный сигнал
. Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n < 0 дискретный сигнал ![]() . При n = 0 значение
. При n = 0 значение ![]() равно значению сигнала
равно значению сигнала ![]() в момент времени t = 0. При n > 0 отсчеты
в момент времени t = 0. При n > 0 отсчеты ![]() повторяют форму сигнала
повторяют форму сигнала ![]() , т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT.
, т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT.
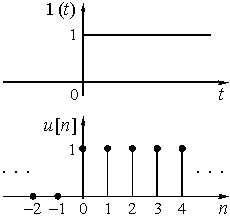
Рис. 2
Дискретные сигналы можно задавать графиками, как это показано на рис. 1, формулами, например, ![]() , в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов.
, в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов.
Пример 1.1. Единичный ступенчатый аналоговый сигнал ![]() приведен на рис. 2.
приведен на рис. 2.
Соответствующий ему дискретный сигнал ![]() называется ступенчатой последовательностью. Он определяется следующим образом:
называется ступенчатой последовательностью. Он определяется следующим образом:

Рис. 3
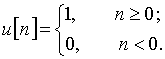
Такая последовательность приведена на рис. 2.
Пример 1.2. Импульс Дирака или d-функция в аналоговой области приведена на рис. 3.

Рис. 4
Дельта-последовательность или дискретная d-функция определяется выражением
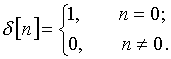
Последовательность ![]() , приведенная на рис. 3, принимает единственное значение, равное 1, при n = 0. Этот сигнал можно сдвинуть на k интервалов:
, приведенная на рис. 3, принимает единственное значение, равное 1, при n = 0. Этот сигнал можно сдвинуть на k интервалов:
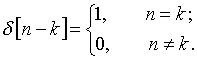
Тогда математическая запись любого дискретного сигнала имеет вид
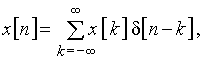
где ![]() – отсчеты исходного аналогового сигнала.
– отсчеты исходного аналогового сигнала.
Этот сигнал можно получить из аналогового (рис. 4) периодическим замыканием ключа на очень короткое время в моменты t = k.
Самоконтроль
1. Что представляют собой аналоговые, дискретные и цифровые сигналы?
2. Как практически получить дискретный сигнал из аналогового?
3. Что такое ступенчатая последовательность и дельта-последовательность?
4. Изобразите графики дискретных d-функций ![]() и
и ![]() .
.

