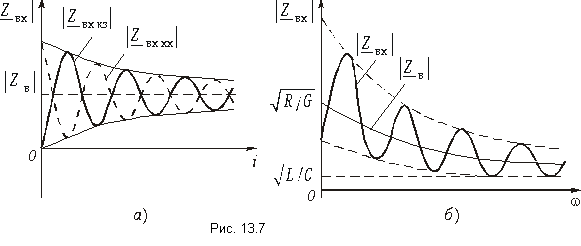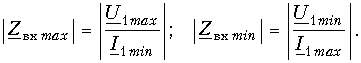Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение для Zвх, используя уравнения передачи линии в форме (13.9 в):
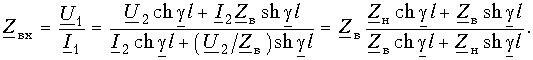
Рассмотрим некоторые частные режимы работы линии.
При согласованном включении линии (Zн = Zв) из (13.16) получим, что Zвх = Zв как и было установлено ранее.
Если выходные зажимы линии замкнуты накоротко (Zн = 0), формула (13.16) упрощается и принимает вид
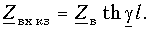 (13.17 а)
(13.17 а)В случае разомкнутых выходных зажимов (Zн = бесконечность)
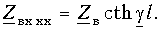
Когда линия нагружена на произвольное сопротивление, не равное волновому (Zн <> Zв), можно пользоваться для расчетов общей формулой (13.16). Однако иногда удобно выразить Zвх через параметры XX и КЗ. Для этого разделим числитель и знаменатель (13.16) на
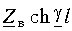
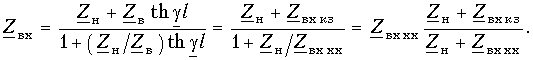
Данная формула позволяет по измеренным значениям сопротивлений XX и КЗ рассчитать входное сопротивление линии.
Существует еще одна форма представления входного сопротивления. Для получения ее перепишем выражение (13.16) после деления на
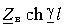
в другом виде:
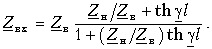
Обозначим
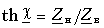 .
.
Тогда
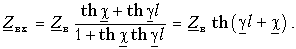
Эта формула дает возможность по заданным параметрам Zв и Zн определить
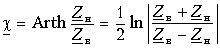
и затем найти входное сопротивление линии.
Во всех случаях, когда нагрузка на конце линии не равна ее волновому сопротивлению, входное сопротивление определяется гиперболическим тангенсом комплексного аргумента. Чтобы дать представление о характере изменения входного сопротивления линии, на рис. 13.7, а показаны зависимости модулей сопротивлений XX и КЗ от длины линии, построенные в соответствии с формулами (13.17), а на рис. 13.7, б изображена зависимость модуля Zвх от частоты из (13.18) при несогласованной нагрузке линии.