Эффективное разделение сигналов может быть осуществлено только на основе строгой теории, в которой формулируются условия разделения и даются количественные оценки различных способов разделения. Возможны два подхода к решению этой проблемы: геометрический и аналитический. С принципиальной точки зрения оба эти подхода равноценны. Геометрическая теория различения (разделения) сигналов была рассмотрена в § 2.11. Ниже рассматривается аналитическая теория разделения (линейной селекции). Основы этой теории были разработаны Д. В. Агеевым в 1935 г.
Пусть канальные сигналы записаны в виде
![]() (10.5)
(10.5)
где ![]() — переносчик, а
— переносчик, а ![]() — коэффициент, отображающий передаваемое сообщение по k-му каналу. Произведение
— коэффициент, отображающий передаваемое сообщение по k-му каналу. Произведение ![]() представляет результат модуляции переносчика
представляет результат модуляции переносчика ![]() сообщением
сообщением ![]() . Различие между канальными сигналами — это различие между переносчиками
. Различие между канальными сигналами — это различие между переносчиками ![]() .
.
Линейный сигнал представляет собой сумму канальных сигналов
![]() (10.6)
(10.6)
Этот сигнал передается по линии связи. На приемном конце для разделения сигналов имеется п разделительных (избирательных) устройств. Действие этих устройств будем описывать оператором разделения ![]() . Далее мы предполагаем, что помехи в канале отсутствуют.
. Далее мы предполагаем, что помехи в канале отсутствуют.
Сущность разделения состоит в том, что каждое из избирательны устройств должно реагировать на «свой» сигнал и не реагировать на все остальные. Математически это запишется в виде
![]() (10.7)
(10.7)
где
![]()
Необходимым и достаточным условием разделимости сигналов ![]() является
является
условие их линейной независимости, которое состоит в том, что тождество
![]() (10.8)
(10.8)
удовлетворяется только в том единственном случае, когда все коэффициенты одновременно равны нулю.
Линейно-независимой называется такая система функций ![]() , при которой ни одна из них не может быть выражена в виде линейной комбинации остальных. Если можно подобрать такие не равные нулю значения
, при которой ни одна из них не может быть выражена в виде линейной комбинации остальных. Если можно подобрать такие не равные нулю значения ![]() , что тождество (10.8) удовлетворяется, то функции
, что тождество (10.8) удовлетворяется, то функции ![]() зависимы. Действительно, если, например,
зависимы. Действительно, если, например, ![]() и
и ![]() не равны нулю, то при
не равны нулю, то при ![]() функция
функция ![]() есть с масштабным множителем
есть с масштабным множителем![]() .
.
Большой практический интерес представляет случай, когда канальные сигналы образуют ортогональную систему функций ![]() , что является достаточным, но не необходимым условием для их разделимости. Условие ортогональности записывается в виде
, что является достаточным, но не необходимым условием для их разделимости. Условие ортогональности записывается в виде
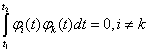 (10.9)
(10.9)
Будем считать, кроме того, что функции ![]() нормированы так, что
нормированы так, что
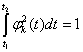 (10.10)
(10.10)
Линейный сигнал пусть представляется суммой
![]() (10.11)
(10.11)
При этих условиях разделение сигналов сводится к нахождению коэффициентов разложения s(t) по ортогональным нормированным функциям ![]() . Умножая (10.11) на
. Умножая (10.11) на ![]() и интегрируя, получим
и интегрируя, получим
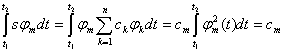
Следовательно, оператор разделения Фтв этом случае имеет вид
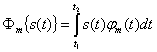 (10.12)
(10.12)
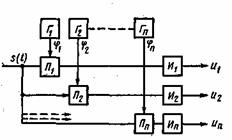
Рис. 10.5. Схема разделения ортогональных сигналов
Результатом этой операции является выделение величины ст, т. е. сообщения соответствующего канала.
Структурная схема устройства, разделяющего ортогональные сигналы, показана на рис. 10.5. Она состоит из п корреляторов, каждый из которых выделяет соответствующий сигнал и восстанавливает переданное сообщение.
Общая теория, изложенная выше, есть в сущности, теория разделения сигналов по форме. Известные способы разделения по частоте, фазе и по времени являются частными случаями этого общего метода разделения.
В случае фазового разделения канальные сигналы с учетом нормировки запишутся в виде:
![]()
Линейный сигнал представляется суммой
![]()
Разделение происходит следующим образом:
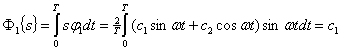
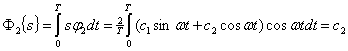
При временном разделении по линии в любой момент времени передается только один сигнал. Поэтому условие линейной независимости (10.8) вырождается в равенство ![]() , а это возможно только при
, а это возможно только при ![]() . Оператором разделения k-го канала
. Оператором разделения k-го канала ![]() в данном случае является временная характеристика коммутатора K, равная единице при замыкании и нулю при размыкании(рис. 10.3).
в данном случае является временная характеристика коммутатора K, равная единице при замыкании и нулю при размыкании(рис. 10.3).
При частотном разделении условие линейной независимости канальных сигналов вытекает из того, что сигналы занимают не перекрывающиеся полосы частот. Оператором разделения k-гo канала ![]() является фильтр, который пропускает только частоты этого канала и совершенно не пропускает частоты всех других каналов.
является фильтр, который пропускает только частоты этого канала и совершенно не пропускает частоты всех других каналов.
Система линейно-зависимых функций, как известно, может быть ортогонализована, т. е. путем линейного преобразования заманена системой ортогональных функций. Следовательно, разделение линейно-независимых сигналов всегда можно свести к разделению ортогональных функций.

