Передача информации в радиотехнических системах связана со спектральными преобразованиями сигналов. Но если спектральные характеристики детерминированных сигналов достаточно просто определяются преобразованием Фурье

,

где – детерминированная функция, описывающая сигнал,

– его спектр, т.е. распределение комплексных амплитуд по частоте, то для случайного процесса понятие комплексной амплитуды отсутствует. И тем не менее для случайного процесса можно ввести удобную спектральную характеристику.

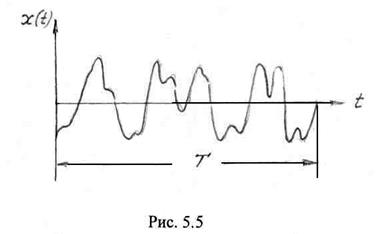
Рассмотрим эргодический центрированный случайный процесс. Если выбрать из ансамбля реализаций процесса какую-либо конкретную реализацию (фотографию процесса) достаточно большой длительности (рис. 5.5), то она представляет детерминированную функцию (мы ее наблюдаем и нам известны все изменения случайного процесса). Поэтому к такой реализации можно формально применить преобразование Фурье и вычислить ее спектр

.

Найдем энергию рассматриваемой реализации. Согласно равенству Парсеваля энергия реализации длительностью равна

. (5.57)

Очевидно, при энергия реализации неограниченно возрастает. Поэтому целесообразно перейти от энергии реализации к средней мощности на интервале . Для этого разделим обе части равенства (5.57) на

. (5.58)

Отношение представляет собой спектральную плотность средней мощности, т.е. среднюю мощность, приходящуюся на единицу полосы частот и имеет размерность .

Функция

, (5.59)

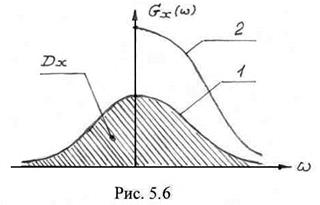
характеризует энергетический спектр, т.е. распределение средней мощности по частоте. На рис. 5.6 изображен энергетический спектр случайного процесса. Отметим некоторые свойства функции энергетического спектра:

– энергетический спектр является вещественной неотрицательной функцией частоты ;

– энергетический спектр является четной функцией частоты, т.е. (кривая 1 на рис. 5.5). На этом основании часто используют функцию

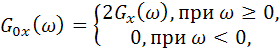
называемую односторонним энергетическим спектром (кривая 2 на рис. 5.6).

Так как мы рассматриваем центрированный случайный процесс, т.е. процесс у которого исключено математическое ожидание (постоянная составляющая), очевидно средняя мощность любой его реализации равна дисперсии процесса. Тогда можно записать

. (5.60)

Иными словами, дисперсия процесса равно площади под кривой .

В заключение отметим, что в технических расчетах вместо часто используют энергетический спектр как функцию циклической частоты

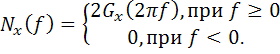(5.61)