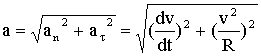2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений

2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения

2.1.3. Кинематические характеристики. Скорость

2.1.4. Кинематические характеристики. Ускорение

2.1.5. Поступательное и вращательное движение твердого тела

2.1.6. Связь между кинематическими характеристиками при различных видах движений

2.1.1. Механическое движение. Физические модели реальных тел, используемые в механике. Система отсчета. Траектория. Виды движений

1. Механическое движение - изменение положения тела или отдельных его частей в пространстве с течением времени.

Внутреннее строение движущихся тел, их химический состав не влияет на механическое движение. Для описания движения реальных тел в зависимости от условий задачи пользуются различными моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и т.д.

Материальной точкой называется тело, размерами и формой которого можно пренебречь в условиях данной задачи. В дальнейшем вместо термина "материальная точка" будем употреблять термин "точка". Одно и то же тело можно свести к материальной точке в одной задаче, и необходимо учитывать его размеры в условиях другой задачи. Например, расчет движения самолета, летящего над Землей, можно производить, считая его материальной точкой. А при расчете обтекания воздухом крыла того же самолета надо учитывать форму и размеры крыла.

Любое протяженное тело можно рассматривать как систему материальных точек.

Абсолютно твердое тело (а.т.т.) - тело, деформацией которого можно пренебречь в условиях данной задачи. А.т.т. можно рассматривать как систему жестко связанных между собой материальных точек, т.к. расстояние между ними не изменяются при любых взаимодействиях.

Абсолютно упругое тело - тело, деформация которого подчиняется закону Гука (см. § 2.2.2.), и после прекращения силового воздействия оно полностью восстанавливает первоначальные размеры и форму.

Абсолютно неупругое тело - тело, которое после прекращения силового воздействия на него не восстанавливается, а полностью сохраняет деформированное состояние.

2. Для определения положения тела в пространстве и во времени надо ввести понятие системы отсчета. Выбор системы отсчета произволен.

Системой отсчета называется тело или группа тел, считающиеся условно неподвижными и снабженные устройством отсчета времени (часами, секундомером и т.д.), относительно которых рассматривается движение данного тела.

Неподвижное тело (или группу тел) называют телом отсчета и для удобства описания движения с ним связывают систему координат (декартову, полярную, цилиндрическую и т.д.).

Выберем в качестве системы координат декартову прямоугольную систему XYZ (подробно см.[8]). Положение точки С в пространстве можно определить координатами х, y, z (Рисунок 1).

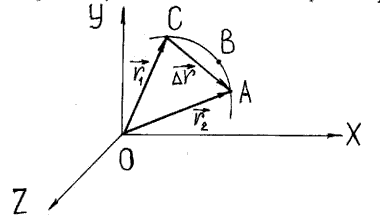
Рисунок 1 - Определение положения точки в декартовой системе координат

Однако положение той же точки в пространстве можно задать с помощью одной векторной величины r = r(x, y, z), называемой радиус-вектором точки С (Рисунок 1).

3. Линия, которую тело описывает при своем движении, называется траекторией. По виду траектории движения можно разделить на прямолинейные и криволинейные. Траектория зависит от выбора системы отсчета. Так, траектория движения точек винта самолета относительно летчика - окружность, а относительно Земли - винтовая линия. Другой пример: какова траектория движения кончика иглы проигрывателя относительно пластинки? корпуса проигрывателя? корпуса звукоснимателя? Ответы таковы: спираль, дуга окружности, состояние покоя (игла неподвижна).

2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения

1. При движении тела относительно выбранной системы координат его положение изменяется с течением времени. Движение материальной точки будет полностью определено, если заданы непрерывные и однозначные функции времени t:

x = x(t), y = y(t), z = z(t).

Эти уравнения описывают изменение координат точки от времени и называются кинематическими уравнениями движения.

2. Путь - часть траектории, пройденной телом за определенный промежуток времени. Момент времени t₀, от которого начинается его отсчет, называется начальным моментом времени, обычно t₀=0 в силу произвольного выбора начала отсчета времени.

Длиной пути называется сумма длин всех участков траектории. Длина пути не может быть величиной отрицательной, она всегда положительна. Например, материальная точка переместилась из точки траектории С сначала в точку А, а затем в точку В (Рисунок 1). Длина ее пути равна сумме длин дуги СА и дуги АВ.

2.1.3. Кинематические характеристики. Скорость

1. Для характеристики быстроты движения тел в физике вводится понятие скорости. Скорость - вектор, а значит, характеризуется величиной, направлением, точкой приложения.

Рассмотрим движение вдоль оси Х. Положение точки будет определяться изменением со временем координаты Х.

Если за время ∆ произошло перемещение точки на ∆r, то величина является средней скоростью движения: .

Средней скоростью движущегося тела называется вектор, равный отношению вектора перемещения к величине промежутка времени, за которое это перемещение произошло.

Модуль средней скорости есть физическая величина, численно равная изменению пути за единицу времени.

2. Для определения скорости в данный момент времени, мгновенной скорости, нужно рассмотреть интервал времени ∆t→0, тогда

Используя понятие производной, можно записать для скорости

Скорость тела в данный момент времени называется мгновенной скоростью (или просто скоростью).

Вектор V мгновенной скорости направлен по касательной к траектории в сторону движения тела.

2.1.4. Кинематические характеристики. Ускорение

1. Быстрота изменения вектора скорости характеризуется величиной, называемой ускорением. Ускорение может возникнуть как за счет изменения величины скорости, так и за счет изменения направления скорости.

Пусть в момент времени t скорость тела равна v₁, а через промежуток времени ∆t в момент времени t + ∆t равна v₂, приращение вектора скорости за ∆t равно ∆v.

Средним ускорением тела в интервале времени от t до t + ∆t называется вектор а_ср, равный отношению приращения вектора скорости ∆v к промежутку времени ∆t:

Cреднее ускорение есть физическая величина, численно равная изменению скорости за единицу времени.

2. Для определения ускорения в данный момент времени, т.е. мгновенного ускорения, нужно рассмотреть малый интервал времени ∆t→0. Тогда вектор мгновенного ускорения равен пределу вектора среднего ускорения при стремлении промежутка времени ∆t к нулю:

Используя понятие производной, можно дать для ускорения следующее определение: Ускорением (или мгновенным ускорением) тела называется векторная величина а, равная первой производной по времени от скорости тела v или второй производной по времени от пути.

3. При вращении точки по окружности ее скорость может изменяться по величине и по направлению (рисунок 2)

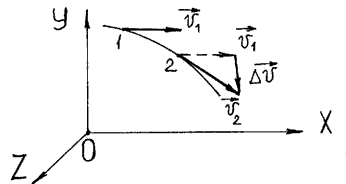
Рисунок 2 - Изменение скорости точки при вращении по окружности

На рисунке 2 в положении 1 скорость точки v_1, в положении 2 скорость точки v₂. Модуль скорости v₂ больше модуля скорости v₁ , ∆v- вектор изменения скорости ∆v = v₂ -v₁

Вращающаяся точка имеет тангенциальное ускорение, равное а_τ=dv/dt, оно изменяет скорость по величине и направлено по касательной к траектории; и нормальное ускорение, равное а_n= v²/R, оно меняет направление скорости и направлено по радиусу окружности (R) (см. Pисунок 3)

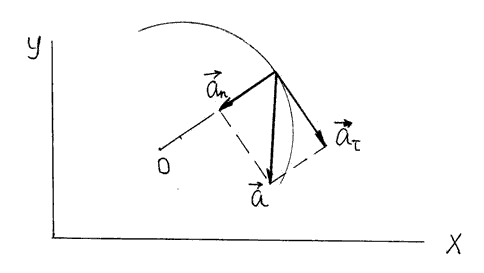
Рисунок 3 - Полное, тангенциальное и нормальное ускорения вращающейся точки

Вектор полного ускорения равен , т.е. он может быть представлен как сумма векторов тангенциального a_τ и нормального a_n ускорений. Модуль полного ускорения равен:

2.1.5. Поступательное и вращательное движение абсолютно твердого тела

1. До сих пор речь шла о характере движения, о траектории, о кинематических характеристиках, но не рассматривалось само движущееся тело. Пример. Движется автомобиль. Он является сложным телом. Движения его кузова и колес различны. Если тело сложное, то возникает вопрос: к движению каких частей тела относятся понятия пути, скорости, ускорения, введенные ранее?

Прежде, чем ответить на этот вопрос, надо выделить формы механического движения. Каким бы сложным не было движение тела, его можно свести к двум основным: поступательному движению и вращению вокруг неподвижной оси. Колебательное движение будет рассмотрено отдельно. В примере с автомобилем поступательно движется кузов автомобиля. Сам автомобиль является телом, которое может быть рассмотрено с помощью модели абсолютно твердого тела (а.т.т.). Для краткости мы будем называть абсолютно твердое тело просто твердое тело.

Поступательным движением твердого тела называется движение, при котором любая прямая, проведенная между его двумя точками, остается при движении параллельна самой себе.

Поступательное движение может быть и не прямолинейным движением.

Примеры. 1) В аттракционе "Колесо обозрения" кабинки - люльки, в которых сидят люди, двигаются поступательно. 2) Если стакан с водой перемещать по траектории, представленной на рисунке 5 так, чтобы поверхность воды и направляющая стакана составляли бы прямой угол, то движение стакана является не прямолинейным, но поступательным. Прямая АВ остается при движении стакана параллельна самой себе.

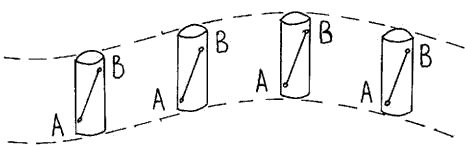
Рисунок 4 - Пример поступательного движения твердого тела.

Особенностью поступательного движения твердого тела является то, что все точки тела описывают одинаковую траекторию, проходят за определенные промежутки времени ∆t одинаковые пути и в любой момент времени имеют одинаковые скорости. Поэтому кинематическое рассмотрение поступательного движения твердого тела сводится к изучению движения любой из его точек. Поступательное движение тела может быть сведено к движению материальной точки. В динамике обычно за такую точку принимают центр масс тела. Кинематические характеристики и кинематические уравнения, вводимые для материальной точки, описывают и поступательное движение твердого тела.

2. Движение колес автомобиля отличается от движения кузова. Точки колеса, находящиеся на разных расстояниях от его оси, описывают разные траектории, проходят различные пути и имеют разные скорости. Чем дальше точка находится от оси колеса, тем больше ее скорость, тем больший путь она проходит за определенный промежуток времени. Движение, в котором участвуют колеса автомобиля, называется вращательным. Ясно, что модель материальной точки для описания вращения реального тело не подходит. Но и здесь вместо реального тела (например, колеса автомобиля с деформируемыми шинами и т.д.) используют физическую модель - абсолютно твердое тело.

Вращательным движением твердого тела называется движение, когда все точки тела описывают окружности, центры которых лежат на прямой, называемой осью вращения и перпендикулярной к плоскостям, в которых вращаются точки тела (Рисунок 5).

Так как для разных точек вращающегося тела траектории, пути, скорости различны, то встает вопрос: можно ли найти физические величины, которые имели бы одинаковые значения для всех точек вращающегося тела, Да, оказывается, есть такие величины, они называются угловыми.

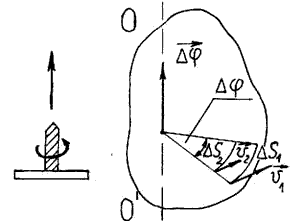
Рисунок 5 - Вращение твердого тела

Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, его положение в пространстве полностью определяется значением угла поворота ∆φ из некоторого начального положения (Рисунок 5). Все точки твердого тела повернутся за промежуток времени ∆ на угол ∆φ.

При малых промежутках времени, когда углы поворота невелики, их можно рассматривать как векторы, хотя и не совсем обычные. Вектор элементарного (бесконечно малого) угла поворота ∆φ направлен вдоль оси вращения по правилу правого буравчика, его модуль равен углу поворота (Рисунок 5). Вектор ∆φ называется угловым перемещением.

Правило правого буравчика заключается в следующем:

Если рукоятка правого буравчика вращается вместе с телом (точкой), то поступательное движение буравчика совпадает с направлением ∆φ.

Другая формулировка правила: Из конца вектора ∆φ видно, что движение точки (тела) происходит против часовой стрелки.

Положение тела в любой момент времени t определяется кинематическим уравнением вращательного движения ∆φ = ∆φ(t).

3. Для характеристики быстроты вращения служит угловая скорость.

Средней угловой скоростью называется физическая величина, равная отношению углового перемещения к промежутку времени, за которое это перемещение произошло

Предел, к которому стремится средняя угловая скорость при ∆→0, называется мгновенной угловой скоростью тела в данный момент времени или просто угловой скоростью вращения твердого тела (точки).

Угловая скорость равна первой производной от углового перемещения по времени. Направление мгновенной угловой скорости определяется по правилу правого буравчика и совпадает с направлением ∆φ (Рисунок 6). Кинематическое уравнение движения для угловой скорости имеет вид ω = ω (t).

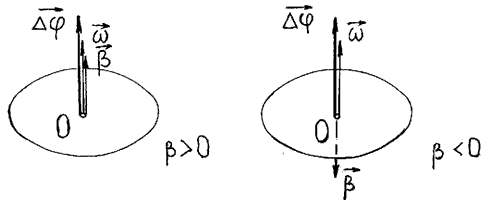
Рисунок 6 - Направление векторов угловых характеристик при вращательном движении.

4. Для характеристики быстроты изменения угловой скорости тела при неравномерном вращении вводится вектор углового ускорения β, равный первой производной от его угловой скорости ω по времени t.

Среднее угловое ускорение есть величина отношения изменения угловой скорости ∆ω к промежутку времени ∆t, за которое это изменение произошло β _ср = ∆ω/∆t

Вектор углового ускорения направлен вдоль оси вращения и совпадает с направлением угловой скорости, если движение ускоренное, и противоположен ему, если вращение замедленное (Рисунок 6).

5. При вращательном движении твердого тела все его точки двигаются так, что вращательные характеристики (угловое перемещение, угловая скорость, угловое ускорение) для них одинаковы. А линейные характеристики движения зависят от расстояния точки до оси вращения.

Связь между этими величинами v, ω, r задается следующим соотношением:

v = [ω∙r],

т.е. линейная скорость v любой точки С твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью ω, равна векторному произведению ω на радиус-вектор r точки С относительно произвольной точки О на оси вращения.

Подобное соотношение существует между линейным и угловым ускорениями вращающейся точки твердого тела:

а = [β∙r].

2.1.6. Связь между кинематическими характеристиками при различных видах движений

По зависимости скорости и ускорения от времени все механические движения делятся на равномерное, равнопеременное (равноускоренное и равнозамедленное) и неравномерное.

Рассмотрим кинематические характеристики и кинематические уравнения, введенные в предыдущих параграфах, для разных видов движений.

1. Прямолинейное движение

Прямолинейное равномерное движение.

Направление движения задается осью ОХ.

Ускорение а = 0 (а_n = 0, а_τ = 0), скорость v = const, путь s = v∙t, координата x = x₀ v∙t, где x₀ - начальная координата тела на оси ОХ.

Путь - величина всегда положительная. Координата может быть и положительной и отрицательной, поэтому в уравнении, задающем зависимость координаты от времени, перед величиной v∙t в уравнении стоит знак плюс, если направление оси ОХ и направление скорости совпадают, и знак минус, если они противоположно направлены.

Прямолинейное равнопеременное движение.

Ускорение а = а_τ = const, а_n = 0, скорость , путь , координата .

Перед величиной (at) в кинематическом уравнении для скорости знак плюс соответствует равноускоренному движению, а знак минус - равнозамедленному движению. Это замечание верно и для кинематического уравнения пути, разные знаки перед величинами (at²/2) соответствуют разным видам равнопеременного движения.

В уравнении для координаты знак перед (v₀t) может быть и плюс, если направления v₀ и оси ОХ совпадают, и минус, если они направлены в разные стороны.

Разные знаки перед величинами соответствуют равноускоренному или равнозамедленному движениям.

Прямолинейное неравномерное движение.

Ускорение а = а_τ>≠ const, а_n = 0,

скорость 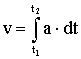, путь .

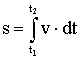2. Поступательное движение

Для описания поступательного движения можно использовать законы, приведенные в §2.1.6. (пункт 2) или §2.1.4. (пункт3). Использование тех или иных законов для описания поступательного движения зависит от его траектории. Для прямолинейной траектории используются формулы из §2.1.6. (пункт 2), для криволинейной - §2.1.4. (пункт3).

3. Вращательное движение

Отметим, что решение всех задач на вращательное движение твердого тела вокруг неподвижной оси аналогично по форме задачам на прямолинейное движение точки. Достаточно заменить линейные величины s, v_х, a_х на соответствующие угловые величины φ, ω, β, и мы получим все закономерности и соотношения для вращающегося тела.

Равномерное вращение по окружности

(R - радиус окружности).

Ускорение: полное а = а_n, нормальное , тангенциальное а_τ = 0, угловое β = 0.

Скорость: угловая ω = const, линейная v = ωR = const.

Угол поворота ∆φ = ∆ φ₀ + ωt, ∆φ₀ - начальное значение угла. Угол поворота величина положительная (аналог пути).

Периодом вращения называется промежуток времени T, в течении которого тело, равномерно вращаясь с угловой скоростью ω, совершает один оборот вокруг оси вращения. При этом тело поворачивается на угол 2π.

.

Частота вращения показывает число оборотов, совершаемых телом за единицу времени при равномерном вращении с угловой скоростью ω:

.

Равнопеременное вращение по окружности

Ускорение: угловое β = const, тангенциальное а_τ = βR=const, нормальное а_n = ω ²R ≠ const, полное

Скорость: угловая ω = ω₀ ( βt), линейная

Угловое перемещение .

Все сказанное ранее относительно знаков в кинематических уравнениях для прямолинейного равнопеременного движения остается верным и для кинематических уравнений вращательного движения: плюс в формулах относится к равноускоренному вращению, минус - к равнозамедленному.

Неравномерное вращение

Ускорение: а_τ = а_τ (t), а_n = а _n(t), β ≠ const,

Скорость:

Угловая ω = dφ/dt, линейная .