Распространение оптических электромагнитных волн может происходить в различных физических средах: в атмосфере, в волоконных световодах, выполненных из различных материалов (стекла, полупроводников, пластмасс), в волноводах интегральных микросхем, в ближнем и дальнем космосе.

Для реализации систем передачи наибольший интерес представляют такие физические среды как стеклянные и полупроводниковые волокна, волноводы микросхем и атмосфера Земли. К важнейшим характеристикам сред распространения оптических излучений необходимо отнести следующие показатели и зависимости.

Показатель преломления среды, смысл которого поясняет соотношение (1.4):

(1.4)

где e и m - показатели диэлектрической и магнитной проницаемости среды, значение n для любого вещества всегда больше 1, т.к. скорость распространения оптических волн v всегда меньше в среде по сравнению с вакуумом с 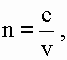(1.5):

(1.5)

Зависимость показателя преломления от длины волны излучения характеризует дисперсию фазовых скоростей распространения света в веществе (рисунок 1.2).

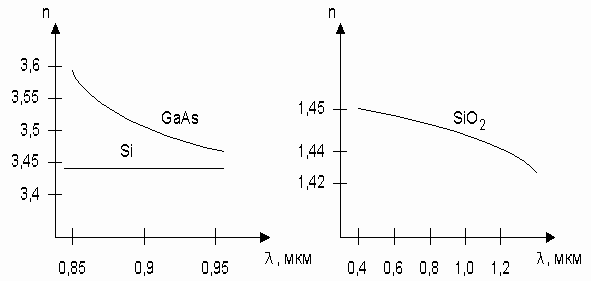
Рисунок 1.2. Зависимость n (l )

Нелинейная зависимость показателя преломления от величины мощности оптического излучения (квадратичная, кубичная)

(1.6)

обусловлена свойствами некоторых сред при высокой плотности мощности светового потока (10⁷...10⁹ Вт/см²). Такая плотность мощности обычно создается лазерными источниками когерентного излучения.

Поглощение оптического излучения в материалах вызвано квантовыми переходами между различными молекулярными уровнями вещества. Например, в стекле (SiO₂) пик поглощения приходится на длину волны 9,2 мкм, однако его "хвост" тянется до диапазона 0,8 ¸ 1,6 мкм. Кроме того, в стеклянных волокнах большую роль играют примеси гидроксильных ионов ОН` переходных металлов Fe, Ni, Cr, V, Cu, которые приводят к большой неравномерности характеристики затухания (рисунок 1.3)

Рассеяние оптического излучения может происходить на малых неоднородностях материалов, габариты которых сопоставимы с длиной оптической волны, в том числе на малых изгибах волноводов.

Характеристика затухания стекловолокна из-за поглощения и рассеяния имеет характер "окон прозрачности" с ограниченными диапазонами частот, которые рекомендованы для систем передачи. При этом параметры затухания нормированы для применения в системах передачи (рисунок 1.4).

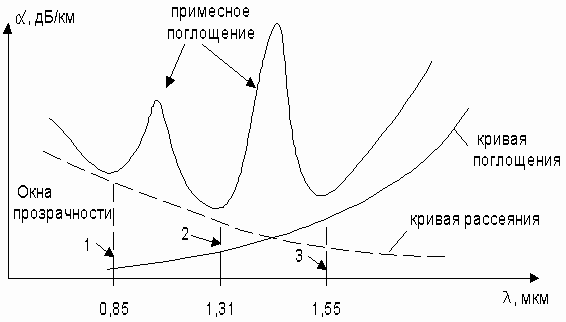
Рисунок 1.3. Спектральные характеристики затухания стеклянного волокна

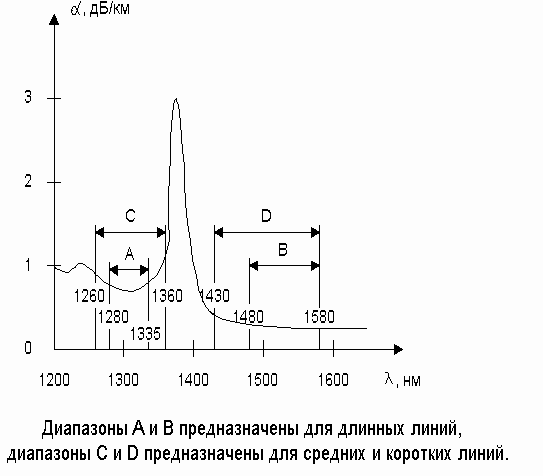
Рисунок 1.4. Нормированная характеристика затухания одномодового стекловолокна согласно рекомендации МСЭ-Т G.957

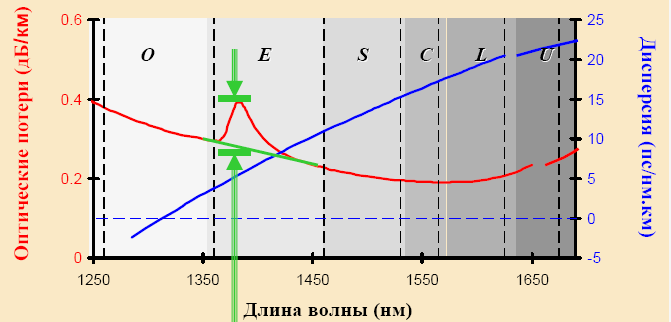
Устранение "водяного" пика

Рисунок 1.5. Характеристики улучшенного стекловолокна G.652

Для волоконных световодов с улучшенными характеристиками, приведенными на рисунке 1.5 (без "водяных пиков" и примесного поглощения), определены оптические диапазоны волн передачи (таблица 1.1)

Таблица 1.1. Оптические диапазоны улучшенного стекловолокна G.652

О – диапазон	1260-1360 нм	Основной
E – диапазон	1360-1460 нм	Расширенный
S – диапазон	1460-1530 нм	Коротковолновый
C – диапазон	1530-1565 нм	Стандартный
L – диапазон	1565-1625 нм	Длинноволновый
U – диапазон	1625-1675 нм	Сверхдлинный

Распространение оптического излучения в атмосфере сопровождается двумя существенными для оптической линии связи процессами: флуктуациями принимаемого сигнала из-за рефракции излучения на турбулентных неоднородностях воздуха и аэрозольными рассеянием и поглощением на частицах дождя, тумана, снега, промышленных выбросах, пыли. Кроме того, поглощение излучения в атмосфере зависит от длины волны, и эта зависимость имеет характер окон прозрачности (рисунок 1.6).

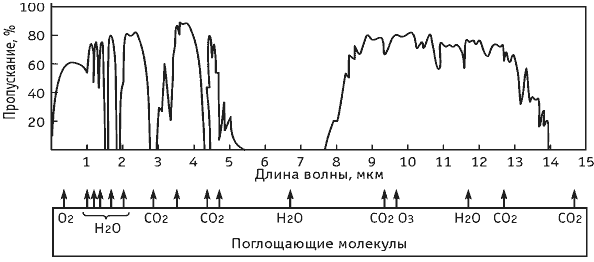
Рисунок 1.6. Поглощение оптического излучения атмосферой

Поглощение света атмосферой зависит и от содержания в ней водяных паров и углекислого газа вдоль пути распространения световой волны, концентрация которых в свою очередь зависит от влажности воздуха и высоты [8].

Конструкции оптических волноводов и оптические характеристики материалов волноводов определяют целый ряд параметров сред передачи оптических сигналов: апертуру ввода излучений в волновод; модовый спектр волновода; затухание; дисперсионные искажения оптических импульсов, возникающие из-за различной скорости распространения спектральных компонентов в волноводе (рисунок 1.7), поляризационную чувствительность[6].

Величина дисперсии оценивается квадратичной разностью (1.7):

D(λ)= (1.7)

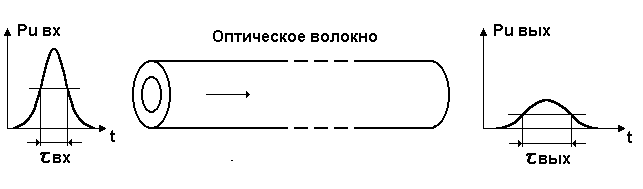
Рисунок 1.7. Дисперсия оптического импульса

Причинами дисперсии в оптоволокне принято считать [7]:

• различие скорости распространения световых мод, образующих межмодовую дисперсию (t _{м м});

• направляющие свойства оптического волновода, образующие волноводную дисперсию (t _в);

• свойства материала оптоволокна, создающие материальную дисперсию (t _м);

• различие скоростей распространения двух взаимно перпендикулярных составляющих моды, обусловленных двойным лучепреломлением волокна, образующее поляризационную модовую дисперсию (t _{п м}).

Дисперсия имеет размерность [с/км].

Волноводная и материальная дисперсия образуют хроматическую, зависящую от ширины спектра моды излучения. Поэтому хроматическая дисперсия имеет размерность [с/нм×км], где нм – единица ширины спектра излучения.

Поляризационная модовая дисперсия имеет размерность [с/Ö км].

Совокупная дисперсия оптического волокна оценивается соотношением (1.8):

D²(λ)= (1.8)

В многомодовых волокнах преимущественно учитывается t _{м м}.

В одномодовых волокнах учитывается сумма t _м+ t _в и при высоких скоростях передачи данных (около 10 Гбит/с и выше) - t _{п м}. Однако сумма t _м+ t _вможет быть близкой к нулю, что обусловлено различным характером дисперсии, которая , в свою очередь, определяется конструкцией волновода.

Дисперсия оптических импульсов в среде распространения может привести к межсимвольным помехам в сигналах и искажению передаваемых сообщений, поэтому дисперсия в волоконно-оптических линиях связи имеет нормированные значения для определенных спектральных диапазонов (рисунки 1.5, 1.8, 1.9). Это волоконные световоды с нулевой дисперсией на волне 1310 нм (SM, по рекомендации G.652), световоды со смещенной (DS, по рекомендации G.653) и смещенной ненулевой дисперсией (NZDS, по рекомендациям G.655, G.656): Tera Light, Pure Guide, E-LEAF, True Wave.

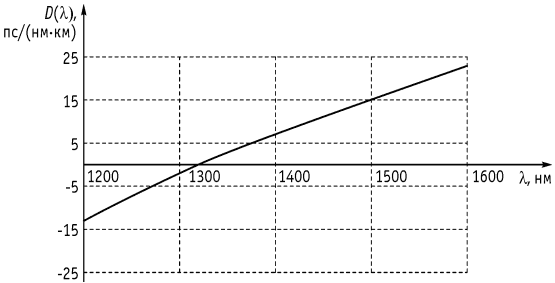
Рисунок 1.8. Характеристика дисперсии одномодового стекловолокна SM, оптимизированного для длины волны 1.31 мкм

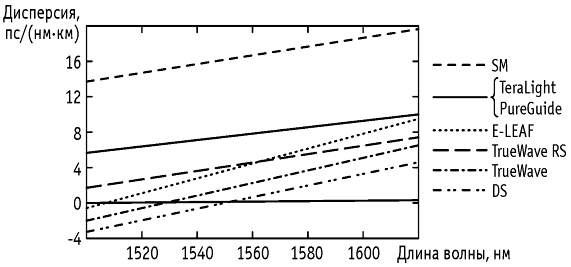
Рисунок 1.9. Характеристика дисперсии одномодовых стекловолокон SM, DS, NZDS для длины волны 1.55 мкм

На рисунке 1.10 представлены характерные значения показателей преломления сердцевины и оболочки для одномодовых волокон SM и NZDS.

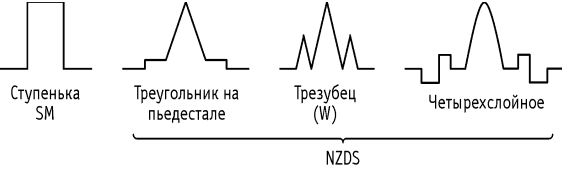
Рисунок 1.10. Характеристики показателей преломления одномодовых стекловолокон для минимума дисперсии на 1310нм и около 1550 нм

С другими примерами характеристик затухания и дисперсии волоконных световодов можно детально ознакомиться в литературе [2, 4, 6, 7, 8, 10, 12, 17].

Нелинейно-оптические эффекты в средах распространения рассматриваются как результат взаимодействия оптического излучения (оптического поля) с множеством атомов и молекул. Эти эффекты могут приводить как к поглощению световых волн и их рассеянию, так и к усилению. Для усиления световых волн среда распространения должна иметь инверсное (возбужденное состояние), в котором она может отдавать часть своей энергии световому полю. Подобные среды в технике оптических систем связи представляют собой полупроводниковые и стекловолоконные световоды с редкоземельными примесями (ионами эрбия Er, неодима Nd, празеодима Pr, тулия Tm). Нелинейно-оптические эффекты имеют уже устоявшуюся классификацию и достаточно хорошо изучены [2, 3, 4, 23, 31, 38, 40, 52]:

• вынужденное комбинационное рассеяние и усиление;

• вынужденное бриллюэновское рассеяние;

• фазовая самомодуляция;

• четырехфотонное смешение и некоторые другие [61, 62, 63, 64].

Поляризационные свойства физических сред распространения оптических волн обусловлены оптической неоднородностью (анизотропией) и могут иметь как естественное (природное), так и конструктивное происхождение.

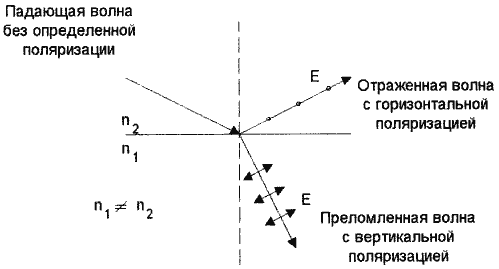
Рисунок 1.11. Поляризация на границе раздела оптических сред

Поляризация световой волны, т.е. придание волне определенных свойств по распределению напряженности электрической и магнитной составляющих поля, может происходить в результате отражения от границы раздела оптических сред с разными показателями преломления (рисунок 1.10).

В средах с анизотропными оптическими свойствами, например, в кварце, исландском шпате, слюде, естественный свет подразделяется на две линейно поляризованные в различных плоскостях волны, которые распространяются с различными скоростями. Это явление называется двойным лучепреломлением.

В ряде изотропных материалов, например, в жидкостях типа нитробензола, возможно искусственное создание эффекта двойного лучепреломления при помещении вещества в сильное электрическое поле. Идея создания определенных свойств оптических материалов реализована в различных приборах на основе линейного электрооптического эффекта Поккельса и нелинейного оптического эффекта Керра [2, 65].

Распространение световых волн в волоконных световодах связано с законами оптики (отражения, преломления) и обусловлено процессами образования оптических мод т.е. определенных типов колебаний. Описание этих процессов можно также найти в многочисленной литературе. Однако для облегчения изучения ряда сложных разделов ниже приведены некоторые определения из классической физики.

При падении луча света на границу раздела двух сред могут наблюдаться следующие эффекты: луч света преломляется; луч света отражается; луч света распространяется вдоль границы раздела сред. Эти эффекты зависят от соотношения показателей преломления сред и угла падения света. Связь этих параметров устанавливает закон Снеллиуса (голландский ученый 1580-1620гг):

, (1.9)

где a – угол падения, b – угол преломления, V₁ –скорость света в среде 1, V₂ – скорость света в среде 2. На рисунке 1.12 приведен пример распространения света на границе раздела сред.

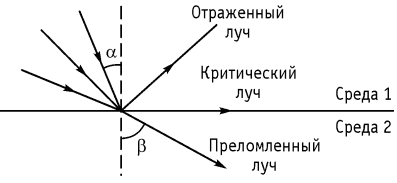
Рисунок 1.12. Световые лучи на границе раздела физических сред

Условие Брэгга-Вульфа устанавливает связь периодической среды с направлением эффективно дифрагирующих лучей света и длиной волны излучения

2×d×SinQ = m×λ, (1.10)

где d- расстояние между отражающими элементами, Q- угол между падающим лучом и отражающей плоскостью, λ- длина волны излучения, m- порядок дифракции. Для справки: Брэгг У.Л. (1862-1942гг) английский физик, Вульф Г.В. (1863-1925) российский физик.