2.5.1. Геометрические и оптические параметры оптических волокон

2.5.2. Параметры передачи оптических волокон

2.5.3. Механические параметры оптических волокон

2.5.1. Геометрические и оптические параметры оптических волокон

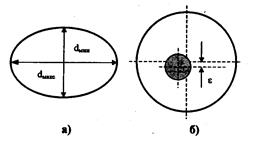
Рис. 2.25. Примеры неоднородностей в ОВ: а – некруглость; б – неконцентричность сердцевины и оболочки ОВ

Основными геометрическими параметрами ОВ являются: диаметр сердцевины; диаметр оболочки; диаметр защитного покрытия; некруглость (эллиптичность) сердцевины; некруглость оболочки; неконцентричность сердцевины и оболочки.

Некруглость сердцевины ОВ определяется как разность максимального и минимального диаметров сердцевины, деленная на номинальный диаметр сердцевины, и определяется только в многомодовых волокнах, некруглость оболочки — в многомодовых и одномодовых волокнах. Некруглость сердцевины ОВ (рис 2.25 а) определяется из выражения:

(2.64) где Н_­с — некруглость сердцевины, %; d_макс, d_мин — наибольший и наименьший диаметр сердцевины, мкм, соответственно; d_н — номинальный диаметр сердцевины, мкм.

Некруглость оболочки ОВ определяется аналогично.

Неконцентричность сердцевины относительно оболочки определяется как расстояние между центрами оболочки и сердцевины ОВ (рис. 2.25 б) и определяется из выражения:

(2.65)

где Н_с/о — неконцентричность сердцевины относительно оболочки, мкм; Ц_с — координаты центра сердцевины, мкм; Ц_о — координата центра оболочки, мкм.

Геометрические параметры стандартизированы для разных типов ОВ [9, 10, 11, 12, 13].

Поэтому остановимся более подробно на оптических параметрах ОВ.

Основными оптическими параметрами волокна являются:

• относительная разность показателей преломления (Δ);

• числовая апертура(NА);

• нормированная частота (v);

• число распространяющихся мод (М);

• диаметр модового поля (d_мп);

• длина волны отсечки (критическая длина волны λ_кр).

Относительная разность показателей преломления. Относительная разность ПП сердцевины и оболочки ОВ определяется выражением (2.12).

Числовая апертура. Одной из основных характеристик, определяющих условия ввода оптических сигналов и процессы их распространения в ОВ, является числовая апертура, определяемая для:

• оптических волокон со ступенчатым ППП

(2.66)

• оптического волокна с градиентным профилем ППП

(2.67)

В градиентных ОВ используется понятие локальной числовой апертуры. Ее значение

максимально на оси волокна и равно 0 на границе раздела сердцевина — оболочка.

Нормированная частота. Этот параметр, определяющий число мод, равен:

(2.68)

где λ — длина волны, мкм.

Если 0<v<2,405, то режим работы волокна одномодовый, если v>2,405 — многомодовый. Чем меньше диаметр сердцевины ОВ, тем меньшее число мод может распространяться по нему и тем меньшее расширение получают оптические импульсы. Соответственно увеличивается коэффициент широкополосности ОВ. Таким образом, одномодовое (ООВ) может передавать более широкополосные сигналы, чем многомодовое (МОВ).

Число мод в многомодовом оптическом волокне. Общее число мод в МОВ с диаметром сердцевины 2а, заданной числовой апертурой на рабочей длине волны λ определяется через нормированную частоту выражением вида:

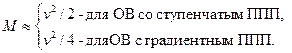(2.69)

В расчетах М может оказаться дробным числом, в то время как число мод в волокне бывает только целым и составляет от одной до тысячи мод. В волокне с градиентным ППП и теми же значениями диаметра сердцевины, показателей преломления п₁ и п₂ число мод примерно в 2 раза меньше, чем в ОВ со ступенчатым ППП. Количество мод (с учетом всех вырожденных мод) в случае ступенчатого ППП (2.2) определяется выражением вида:

(2.70)

где u — показатель степени, описывающий изменения ППП.

Диаметр модового поля в ООВ. Важным интегральным параметром ООВ является диаметр модового поля. Этот параметр используется при анализе одномодовых волокон.

В многомодовых ОВ размер сердцевины принято оценивать диаметром (2а), в одномодовых волокнах — с помощью диаметра модового поля (d_МП). Это связано с тем, что энергия основной моды в ООВ распространяется не только в сердцевине, но и частично в оболочке, захватывая ее приграничную область. Поэтому d_МП более точно оценивает размеры поперечного распределения энергии основной моды. Величина d_МП является важной при стыковке волокон между собой, а также при стыковке источника излучения с волокном.

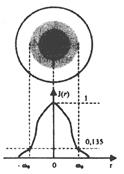
Рис. 2.26. Зависимость распределения интенсивности излучения основной моды ООВ в ближней зоне от радиуса

В [14] показана зависимость распределения интенсивности (мощности) излучения основной моды одномодового волокна в ближней зоне от радиуса (рис.2.26). Эта зависимость аппроксимируется с достаточной степенью точности формулой Гаусса:

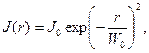(2.71)

где J(r) — интенсивность излучения на расстоянии r от оси ООВ; J₀ — интенсивность излучения на оси ООВ (при r=O); W_o — радиус модового поля, т. е. значение радиуса, при котором интенсивность излучения составляет 1/е² = 0,35J₀ .

Согласно [6, 15] радиус поля моды W_o в микрометрах определяется при известных значениях v и а=d_c/2 из соотношения

или

(2.72)

Тогда искомое значение диаметра модового поля равно d_МП=2W₀.

Длина волны отсечки в ООВ. Минимальная длина волны, при которой ОВ поддерживает только одну распространяющуюся моду, называется длиной волны отсечки. Этот параметр характерен для ООВ. Если λ_кр меньше, чем длина волны отсечки, то имеет место многомодовый режим распространения света.

Согласно [10] различают длину волны отсечки в волокне λ_с и длину волны отсечки в волокне λ_с и длину волны отсечки в проложенном кабеле λ_сс. Первая (λ_с) соответствует слабо напряженному волокну и для ступенчатого ООВ она определяется выражением вида:

(2.73)

Длина отсечки в проложенном кабеле λ_сс соответствует напряженному ОВ. На практике ОВ в проложенном или подвешенном на опорах кабеле имеет большое число изгибов. Кроме того, сильные искривления имеются в ОВ, уложенных в кассеты муфт и промежуточных соединителях на объектах связи (сплайс-боксах). Все это ведет к подавлению побочных мод и сдвигу λ_сс в сторону коротких длин волн в сравнении с λ_с. Разницу между λ_сс и λ_с можно оценить только экспериментальным путем.

2.5.2. Параметры передачи оптических волокон

К параметрам передачи ОВ относятся:

• коэффициент затухания;
• дисперсия ООВ;
• ширина полосы пропускания МОВ.

Коэффициент затухании оптического сигнала. Затухание в оптическом волокне — это мера ослабления оптической мощности, распространяемой вдоль ОВ между двумя его поперечными сечениями на данной длине волны. Затухание в ОВ выражается в дБ. Коэффициент затухания в ОВ — это величина затухания на единице длины волокна и выражается в дБ/км. Коэффициент затухания в ОВ обуславливается собственными потерями волокна и выражается в виде:

, (2.74)

где α_рр, α_пт, α_ик, α_пр — составляющие коэффициента затухания за счет рэлеевского рассеяния, поглощения в материале волокна, инфракрасного поглощения и поглощения на примесях ОВ, соответственно.

В общем виде потери энергии в материале волокна зависят от поглощения световой энергии, наличия посторонних примесей, таких как гидроксильные группы (ОН), ионы металлов (железа, кобальта, никеля, меди) и других включений, а так же от потерь на поглощение передаваемой мощности в инфракрасной области сектора.

Общие потери на поглощение в ОВ определяются формулой:

(2.75)

Механизм основных потерь, возникающих при распространении по ОВ электромагнитной энергии, иллюстрируется рис. 2.27. Часть мощности, поступающей на вход световода Р_вх, рассеивается из-за изменения направления распространяемых лучей на нерегулярностях и их высвечивании в окружающее пространство (α_рр), другая часть мощности поглощается материалом ОВ (α_пм) в виде поляризации диполей ОВ, посторонними примесями, что проявляется в виде Джоулева тепла (α_пр). В результате мощность на выходе P_вых. уменьшается.

Потери на поглощение существенно зависят от чистоты материала и при наличии посторонних примесей могут быть значительными. Потери на рассеяние лимитируют предел минимально допустимых потерь в ОВ.

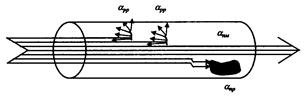
Рис. 2.27. Механизм основных потерь в световодах:

α_рр- рассеяние на нерегулярностях; α_пр- поглощение из-за примесей; α_пм- поглощение в материале волокна

Рассеяние, с одной стороны, обусловлено неоднородностями материала ОВ, размеры которых меньше длины волны, а с другой — тепловыми флуктуациями показателя преломления.

Рассеяние света принципиально неустранимо и вносит свой вклад в затухание ОВ даже в том случае, когда потери света на поглощение равны нулю.

Составляющую коэффициента затухания ОВ α_рр (дБ/км) за счет Рэлеевского рассеяния можно определить из выражения [4, 6]:

(2.76)

где n₁, — ПП сердцевины и равен 1,48 — 1,50; k=l,38·10^-23 Дж/К — постоянная Больцмана; Т=1500К — температура затвердевания стекла при вытяжке; β=8,1·10^-11 м²/Н — коэффициент сжимаемости (для кварца).

Составляющую α_пм (дБ/км), связанную с потерями на диэлектрическую поляризацию, можно определить из выражения:

(2.77)

где n₁ — показатель преломления сердцевины ОВ; tgδ — тангенс угла диэлектрических потерь сердцевины ОВ.

Составляющую α_ик(дБ/км), обусловленную электронным и атомным резонансами в инфракрасной части спектра за счет колебания атомов в кристаллической решетке, можно определить из выражения [6]:

(2.78)

где С и к — постоянные коэффициенты, равные, например, для кварца С=0,9, k=(0,7...0,9)10^-6 м.

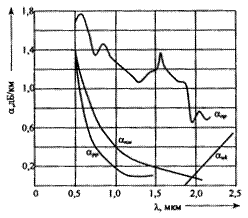
Рис. 2.28. Составляющие потерь энергии

На рис. 2.28 представлены типовые зависимости основных составляющих потерь от длины волны. Как видно из графика, рэлеевское рассеивание α_рр ограничивает нижний предел потерь в левой части, а инфракрасное поглощение α_ик — в правой части спектра волн.

В настоящее время в технике связи в основном применяются кварцевые ОВ, область эффективного использования которых находится в диапазоне длин волн до 2 мкм. При дальнейшем увеличении длины волны из-за значительных величин α_ик в ОВ кварц заменяется на другие материалы. В частности, в [16] сообщается об испытаниях фирмой Хьюз Эйркрафт волокон, выполненных из поликристалла бромистого и бромойодистого таллия и имеющих на длинах волн 4 — 5 мкм коэффициент затухания, равный 0,01 дБ/км.

На более длинных волнах в качестве материала для волокна используются галоидные, халькогенидные и фтористые стекла. По сравнению с кварцевыми волокнами они обладают большей прозрачностью и обеспечивают снижение потерь на несколько порядков. С появлением ОВ из новых материалов становится реальным создание ВОЛС без регенераторов. Известны проекты строительства подводной оптической линии через Атлантический океан протяженностью 6000 км без регенераторов, в которых анализируется возможность применения ОВ из тетрафторида, изиркония и фторида бериллия [17].

Так как теоретические расчеты потерь на рэлеевское рассеяние и поглощение представляют собой сложную задачу и точность таких расчетов мала, то при практических расчетах α удобно применять следующие приближенные формулы [18]:

(2.79)

где α_рр — составляющая коэффициента затухания ОВ за счет рэлеевских потерь, дБ/км; λ — длина волны оптического излучения, введенного в ОВ, нм;

при расчете α_рр в одномодовых ОВ второе слагаемое отбрасывается [8]:

, (2.80)

где α_рр — составляющая а за счет материальных потерь ОВ, дБ/км;

, (2.81)

где α_ик — составляющая α ОВ за счет потерь в инфракрасной области, дБ/км.

Из потерь на примесях в реальных ОВ, выпускаемых в соответствии с требованиями ITU — TG.651, G.652 [9, 10], наиболее сильно проявляются потери на гидроксильном остатке воды (ОН), значения которых согласно [13] следующие:

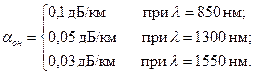(2.82)

При правильном выборе материала для ОВ и рабочей длины волны λ суммарное оценочное значение коэффициента затухания ОВ, выраженное рэлеевскими потерями и общими потерями за счет поглощения, может быть определено согласно [6] выражением:

(2.83)

где α — коэффициент затухания ОВ, дБ/км; k_п = 0,1 —0,25 — экспериментальный поправочный коэффициент, учитывающий потери на поглощение.

Дисперсия оптического сигнала. Наряду с коэффициентом затухания ОВ важнейшим параметром является дисперсия, которая определяет его пропускную способность для передачи информации.

Дисперсия — это рассеивание во времени спектральных или модовых составляющих оптического сигнала, которое приводит к увеличению длительности импульса оптического излучения при распространении его по ОВ (рис. 2.29) и определяется разностью квадратов длительностей импульсов на выходе и входе ОВ [3]:

(2.84)

где значения τ_вых и τ_вх определяются на уровне половины амплитуды импульсов.

Дисперсия не только ограничивает частотный диапазон ОВ, но существенно снижает дальность передачи сигналов, так как чем длиннее линия, тем больше увеличение длительности импульсов. Дисперсия в общем случае определяется тремя основными факторами: различием скоростей распространения направляемых мод, направляющими свойствами оптического волокна и параметрами материала, из которого оно изготовлено. В связи с этим основными причинами возникновения дисперсии являются, с одной стороны, большое число мод в ОВ (межмодовая дисперсия), а с другой стороны — некогерентность источников излучения, реально работающих в спектре длин волн Δλ (хроматическая дисперсия).

Межмодовая (модовая) дисперсия преобладает в многомодовых ОВ. Она обусловлена наличием большого количества мод, время распространения которых различно. Для ОВ со ступенчатым профилем показателя преломления скорость распространения электромагнитных волн с длиной волны λ одинакова и равна:

(2.85)

где с — скорость света, км/с.

В этом случае все лучи, падающие на торец ОВ под углами к его оси в пределах апертурного угла θ_а движутся в сердцевине волокна по своим зигзагообразным линиям и при одинаковой скорости распространения достигают приемного конца в разное время, что естественно, приводит к увеличению длительности принимаемого импульса (рис. 2.29). Все лучи, падающие на торец ОВ под углами к его оси в пределах 0< θ_п < θ_а достигают приемного устройства с некоторым временным сдвигом, что, естественно, приводит к увеличению длительности принимаемого импульса.

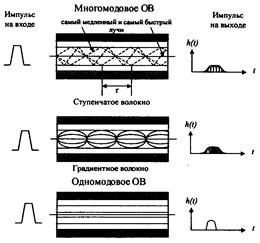
Рис. 2.29. Распространение излучения по ступенчатому и градиентному многомодовым и одномодовому ОВ

Межмодовая дисперсия градиентных ОВ, как правило, на порядок и более ниже, чем у ступенчатых волокон. Это обусловлено тем, что за счет уменьшения показателя преломления от оси ОВ к оболочке скорость распространения лучей вдоль их траекторий изменяется — так, на траекториях, близких к оси, она меньше, а на удаленных, естественно, — больше. Следовательно, лучи, распространяющиеся кратчайшими траекториями (ближе к оси), обладают меньшей скоростью, а лучи, распространяющиеся по более протяженным траекториям, имеют большую скорость. В результате время распространения лучей выравнивается и увеличение длительности импульса становится меньше.

Расширение импульса из-за модовой дисперсии характеризуется временем нарастания сигнала и определяется как разность между самым большим и самым малым временем прихода лучей в сечение световода на расстоянии l от начала.

Согласно законам геометрической оптики время распространения луча в ступенчатом многомодовом ОВ зависит от угла падения О„и, как было показано в [17], определяется выражением:

(2.86)

где L — длина световода, км; n_­1 — показатель преломления сердцевины ОВ; с — скорость света, км/с.

Так как минимальное время распространения оптического луча имеет место при θ_п =0, а максимальное при θ_п = θ_кр, соответствующие им значения времени распространения можно записать: (2.87)

откуда значение межмодовой дисперсии равно:

(2.88)

где τ_мм — межмодовая дисперсия, пс.

Из последнего выражения следует, что межмодовая дисперсия возрастает с увеличением длины волокна. Однако это справедливо только для идеального волокна, в котором взаимодействие между модами отсутствует. В реальных условиях наличие неоднородностей, кручение и изгиб волокна приводят к постоянным переходам энергии из одних мод в другие, т.е. к взаимодействию мод, в связи с чем дисперсия становится пропорциональной . Эго влияние проявляется не сразу, а после определенного расстояния прохождения световой волны, которое носит название длины установившейся связи мод и принимается равным 5 — 7 км для ступенчатого волокна и 10 — 15 км — для градиентного. Оно установлено эмпирическим путем.

В градиентных многомодовых волокнах время распространения оптических лучей определяется законом изменения показателя преломления и при определенных условиях выравнивается, что, естественно, уменьшает дисперсию. Так, при параболическом профиле показателя преломления, когда показатель степени в выражении (2.2) принимает значение и=2,

(2.89)

Наименьший разброс групповых задержек из всех ППП, описываемых (2.2), получается при показателе степени и=и_опт, т.е. при и_опт=2(1 – ) [8]. При этом τ_мод достигает минимального значения (рис. 2.30), равного

(2.90)

Из этого рисунка τ_мод может быть представлено в виде:

(2.91)

Характер кривой на рисунке свидетельствует, что для минимизации дисперсии необходимо тщательно управлять значением и, что на практике оказывается нелегким делом. А всякое изменение профиля, приближающееся к параболическому, существенно уменьшает модовую дисперсию в таком градиентном ОВ.

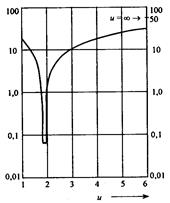
Рис. 2.30. Зависимость модовой дисперсии ΔτСП от степени и в градиентных ОВ

При анализе выражений (2.88) и (2.89) становится очевидным, что межмодовая дисперсия градиентного ОВ в раз меньше, чем у ступенчатого при одинаковых значениях . А так как обычно 1 %, то межмодовые дисперсии указанных ОВ могут отличаться на два порядка.

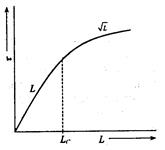
Рис. 2.31. Длина взаимодействия мод

В инженерных расчетах при определении модовой дисперсии следует иметь ввиду, что до определенной длины линии L_с нет межмодовой связи, а затем при L>L_с происходит процесс взаимного преобразования мод и наступает установившийся режим. Поэтому, как видно из рис. 2.31, вначале, при L< L_с, дисперсия увеличивается по линейному закону, а затем, при L>L_с по квадратичному закону. Следовательно, вышеприведенные формулы расчета модовой дисперсии справедливы лишь для длины линии L>L_с.

При длинах линии L>L_с следует пользоваться следующими формулами:

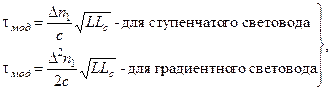(2.92)

где L — длина линии, км; L_c — длина связи мод (установившегося режима), км.

Дисперсионные свойства различных типов ОВ, выпускаемых по рекомендациям ITU-TG.651 и G.652, приведены в табл. 2.5. В ступенчатых световодах при многомодовой передаче доминирует модовая дисперсия и она достигает больших значений (20 — 50 нс/км).

Таблица 2.5. Дисперсионные свойства различных ОВ

Дисперсия	Причина дисперсии	Многомодовое ОВ		Одномодовое ОВ ( F=1-10 ГГц)
		Ступенчатое ( F=10-100 МГц)	Градиентное ( F=100-1000 МГц)
Волноводная	Коэффициент распространения зависит от частоты	Малое значение дисперсии	Малое значение дисперсии	Взаимная компенсация
Материальная	Показатель преломления зависит от частоты	(2 – 5)снс/км	(0,1 – 0,3) нс/км
Межмодовая	Разные моды приходят к концу линии в разное время	(20 – 50) нс/км	(1 – 4) нс/км	Отсутствует

Модовая дисперсия может быть уменьшена следующими тремя способами:

1. использованием ОВ с меньшим диаметром сердцевины, поддерживающей меньшее количество мод. Например, сердцевина диаметром 100 микрон поддерживает меньшее число мод, чем сердцевина в 200 микрон;
2. использованием волокна со сглаженным ППП, чтобы световые лучи, прошедшие по более длинным траекториям, имели скорость, превышающую среднюю, и достигали противоположного конца волокна в тот же момент времени, что к лучи, движущиеся по коротким траекториям;
3. использованием одномодового волокна, позволяющего избежать модовой дисперсии.

В одномодовых ступенчатых световодах отсутствует модовая дисперсия и дисперсия в целом сказывается существенно меньше. Здесь проявляются волноводная и материальная дисперсии и при длине волны порядка 1,3 мкм происходит их взаимная компенсация ( ).

Волноводная (внутримодовая) дисперсия обусловлена процессами внутри моды. Она характеризуется направляющими свойствами сердцевины ОВ, а именно: зависимостью групповой скорости моды от длины волны оптического излучения, что приводит к различию скоростей распространения частотных составляющих излучаемого спектра. Поэтому внутримодовая дисперсия, в первую очередь, определяется профилем показателя преломления ОВ и пропорциональна ширине спектра излучения источника , т.е.

(2.93)

где — удельная внутримодовая дисперсия.

При отсутствии значений оценка характеризуется выражением:

(2.94)

где — ширина спектральной линии источника излучения, равная 1 — 3 нм для лазера и 20 — 40 нм для светоизлучающего диода; L — длина линии,км; с — скорость света, км/с.

Материальная дисперсия в ОВ обусловлена зависимостью показателя преломления от длины волны В реальном ОВ распространение волн дисперсионно, т.е. скорость распространения зависит от частоты (длины волны). Различные длины волн (цвета) также движутся с различными скоростями по волокну, даже в одной и той же моде. Ранее мы видели, что показатель преломления равен n=c/v.

Рис. 2.32. Скорости распространения длин волн

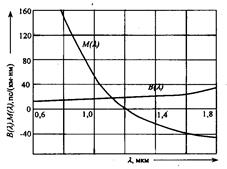
Рис. 2.33. Удельные значения дисперсии при различных длинах волн: В(λ)-волноводная; М(λ)-материальная

Поскольку каждая длина волны движется с разной скоростью, то величина скорости v в этом уравнении изменяется для каждой длины волны. Таким образом, показатель преломления изменяется в зависимости от длины волны. Дисперсия, связанная с этим явлением, называется материальной (молекулярной) дисперсией, поскольку зависит от физических свойств вещества волокна. Уровень дисперсии зависит от диапазона длин волн света, инжектируемого в волокно (как правило, источник излучает несколько, длин волн), а также от центральной рабочей длины волны источника. В области 850 нм более длинные волны (более красные) движутся быстрее по сравнению с более короткими (более голубыми) длинами волн. Волны длиной 860 нм движутся быстрее по стеклянному волокну, чем волны длиной 850 нм. В области 1550 нм ситуация меняется: более короткие волны движутся быстрее по сравнению с более длинными; волна 1560 нм движется медленнее, чем волна 1540 нм. В некоторой точке спектра происходит совпадение, при этом более голубые и более красные длины волн движутся с одной и той же скоростью. Это совпадение скоростей происходит в области 1300 нм, называемой длиной волны с нулевой дисперсией (рис. 2.33). Длина стрелок соответствует скорости длин волн; следовательно, более длинная стрелка соответствует более быстрому движению. Типичная картина удельной волноводной и материальной дисперсии вещества одномодового волокна приведена на рис. 2.33. На длине волны 1300 нм равна нулю. В области длин волн выше 1300 нм она отрицательна — волны отстают и прибывают позднее. В области менее 1300 нм волны опережают и прибывают раньше.

Как и волноводную дисперсию, модовую дисперсию можно определить через удельную дисперсию по выражению:

. (2.95)

Величина определяется экспериментальным путем. При разных составах легирующих примесей в ОВ имеет разные значения в зависимости от . Поэтому при инженерных расчетах для определения т можно использовать выражение:

(2.96)

Для определения можно воспользоваться формулой Селмейера для ПП кварцевогo стекла с использованием метода конечных разностей [19], откуда вычисляют величины , после чего находят

(2.97)

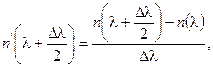(2.98)

а затем

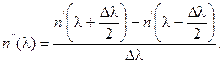(2.99)

Поляризационная модовая дисперсия возникает вследствие разной скорости распространения двух взаимоперпендикулярных поляризаций основной моды ОВ. Для оценки этого вида дисперсии используется выражение:

, (2.100)

где К_пмд — коэффициент удельной поляризационной дисперсии.

По определению поляризационная модовая дисперсия проявляется исключительно в одномодовых волокнах с нециркулярной (эллиптической) сердцевиной и при определенных условиях становится соизмеримой с хроматической дисперсией. Эти условия проявляются тогда, когда используется передача широкополосного сигнала (полоса пропускания 2,4 Гбит/с и выше) с очень узкой спектральной полосой излучения 0,1 нм и меньше.

Поляризационной дисперсии можно дать следующее пояснение. В ООВ распространяется не одна мода, а две фундаментальные моды — две взаимно перпендикулярные поляризации входного сигнала. В идеальном, т.е. однородном по геометрии, волокне две моды распространяются с одинаковой скоростью. Однако реальные ОВ имеют неидеальные геометрические размеры, что приводит к разным скоростям распространения этих двух мод с разными состояниями поляризации и, как следствие, к появлению поляризационной модовой дисперсии.

Поэтому результирующая дисперсия одномодового волокна должна определяться в соответствии с выражением:

(2.101)

В обычных условиях работы ООВ поляризационная модовая дисперсия достаточно мала и поэтому при расчетах полной дисперсии ею можно пренебречь.

В многомодовых ОВ волноводная дисперсия мала по величине, поэтому при определении полной дисперсии ею пренебрегают. В таких ОВ со ступенчатым ППП доминирует над , а с градиентным ППП определяющей становится материальная дисперсия. Последнее связано с тем, что в градиентных МОВ уменьшается за счет выравнивания времени распространения различных мод. Исходя из этого в общем виде полная дисперсия в МОВ может быть представлена выражением:

. (2.102)

В одномодовых ОВ модовая дисперсия отсутствует, так как по таким волокнам распространяется только одна мода НЕ₁₁ или, как отмечалось ранее, две моды в двух разных состояниях поляризации, но с одной дисперсионной зависимостью фазового коэффициента (в приближении линейно-поляризованных мод — LP₀₁ мода в двух взаимоортогональных поляризациях). Другими словами, расширение импульсов в ООВ определяется хроматической дисперсией в пределах этой моды. Тогда полная дисперсия в ООВ может быть представлена в общем виде выражением:

(2.103)

Сравнивая дисперсионные характеристики различных волокон, можно отметить, что наилучшими показателями обладают одномодовые ОВ, а наиболее сильно дисперсия проявляется в многомодовых ОВ со ступенчатым ППП.

Ширина полосы пропускания. Многие производители волокна и оптического кабеля не используют в спецификации дисперсию в многомодовых изделиях. Вместо этого они указывают произведение ширины полосы пропускания на длину, или просто полосу пропускания, выраженную в мегагерцах на километры. Полоса пропускания в 400 МГц км означает возможность передачи сигнала в полосе 400 МГц на расстояние 1 км. Это также означает, что произведение максимальной частоты сигнала на длину передачи может быть меньше или равно 400. Другими словами, можно передавать сигнал более низкой частоты на большее расстояние или более высокой частоты на меньшее расстояние, как показано на рис. 2.34.

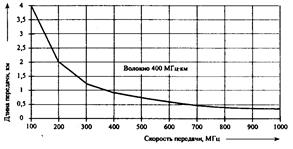
Рис. 2.34. Зависимость длины передачи от ширины полосы пропускания

Рабочая полоса частот (полоса пропускания) ОК определяет число передаваемых по нему каналов связи и лимитируется дисперсией ОВ.

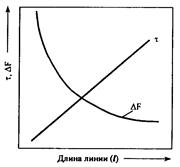
Рис. 2.35. Дисперсия τ и пропускная способность ΔF ОВ различной длины

На рис. 2.35 показан характер изменения дисперсии и пропускной способности ОВ в зависимости от длины линии. Снижение из-за дисперсии величины до допустимого значения лимитирует дальность передачи по ОК.

Полоса частот и дальность передачи l взаимосвязаны. Соотношение между ними выражается формулами (для коротких линий в пределах устанавливающегося модового режима) и (для длинных линий). В этих соотношениях параметры с индексом х — искомые, а без индекса — заданные; l_с — длина связи мод. В реальных условиях обычно формируется полоса пропускания на один километр и определяется полоса пропускания на всю линию по формулам:

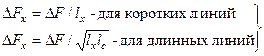(2.104)

Полоса пропускания зависит от расширения импульсов т и определяется соотношением .

2.5.3. Механические параметры оптических волокон

К механическим параметрам ОВ относятся:

• прочность волокна;
• динамическая прочность на разрыв;
• параметр нагрузки разрушения;
• стойкость к изгибам;
• усилие снятия защитного покрытия.

Прочность волокна. Стекло принято считать хрупким. Оконное стекло действительно не гнется. Однако стеклянные волокна можно согнуть в виде окружности небольшого диаметра или завязать в свободный узел, не повреждая их. (Затягивание тугого узла может повредить волокно.)

Предел прочности характеризует способность волокна противостоять натяжению или изгибу без повреждения. Предел прочности волокна на разрыв превосходит ту же величину для стальной нити идентичного размера. Более того, медный проводник должен иметь вдвое больший диаметр, чтобы обеспечить тот же предел точности, что и волокно.

Основная причина, обусловливающая хрупкость волокна, это наличие микротрещин на поверхности и дефектов внутри волокна. При этом поверхностные трещины более существенны. Поверхностные дефекты могут возрастать под воздействием растягивающей нагрузки, возникающей во время прокладки кабеля. Температурные изменения, механические и химические воздействия, обычное старение также приводят к появлению дефектов. Расширяющиеся дефекты приводят к случайному обрыву волокна. Для разрезания стекла делается узкая царапина на его поверхности. Затем, в результате резкого надлома, стекло трескается вдоль царапины. Аналогичный процесс происходит в волокне. Скрытые дефекты действуют аналогично царапине на поверхности стекла. Как только к волокну прикладывается достаточно сильное растягивающее напряжение, дефекты растут внутри волокна до тех пор, пока оно не разрывается.

Динамическая прочность на разрыв. Динамическая прочность ОВ на разрыв — это определенное значение интенсивности нагрузки на растяжение или сжимание, которой подвергается вся длина волокна в его осевом направлении на протяжении определенного кратковременного периода [20].

Величина динамической прочности на разрыв ОВ составляет обычно величину более чем 38 ГПа для образцов, не подвергшихся старению, длиной 0,5 м.

Параметр нагрузки разрушения. Параметр нагрузки разрушения — это безразмерный коэффициент, эмпирически связанный с зависимостью распространения разрушения (трещины) ОВ от приложенной нагрузки [20). Величина параметра нагрузки разрушения зовисит от окружающей температуры, влажности и других условий.

Статистические и динамические значения параметров нагрузки разрушения обычно задаются в технической документации на ОВ. Статические значения параметра нагрузки разрушения (п_с) — это отрицательная крутизна графика зависимости времени наработки ОВ на отказ через статическую усталость в зависимости от приложенной нагрузки в двойном логарифмическом масштабе.

Динамическое значение параметра нагрузки разрушения (п_д) — это такая величина, которая показывает, что значение 1/(п_д+1) есть крутизна графика динамической усталости в двойном логарифмическом масштабе в зависимости от скорости изменения напряжения в волокне, обусловленного приложенной нагрузкой. Значение параметра динамической усталости п_д определяется методом испытания динамической усталости.

Параметры п_с и п_д обычно указываются в технической документации на ОВ и, как пpaвило, их величина больше 20.

Стойкость к изгибам. Несмотря на то, что волокно может быть согнуто в окружность, оно имеет минимальный радиус изгиба. Достаточно резкий изгиб может разорвать волокна. Изгибы также приводят к двум другим эффектам.

1. Слегка увеличивается затухание. Этот эффект должен быть интуитивно понятен. Изгибы изменяют углы падения и отражения света внутри волокна настолько, что часть его, заключенная в модах высокого порядка, может покидать волокно (подобно случаю с микроизгибами).

2. Уменьшается предел прочности волокна на разрыв. Если растяжение сопровождается изгибом волокна, оно может разорваться при меньшем значении растягивающей нагрузки, чем в случае выпрямленного волокна.

Согласно спецификации на ОВ некоторых фирм минимальный радиус кривизны равен пяти диаметрам кабеля при отсутствии растягивающих напряжений и 10 диаметрам кабеля при их наличии.

Усилие снятия защитного покрытия. Этот параметр характеризует усилие, которое необходимо приложить для удаления покрытия с волокна, не подвергая последнее чрезмерному механическому напряжению, которое может привести к его разрыву. Как правило, усилие снятия защитного покрытия ОВ составляет величину, находящуюся в пределе от 1,3 Н до 9 Н.