В 1933 году в работе «О пропускной способности «эфира» и проволоки в электросвязи» В.А. Котельников доказал теорему, ставшую основополагающей в теории и технике цифровой связи. Она гласит: если непрерывный сигнал ![]() имеет спектр, ограниченный частотой
имеет спектр, ограниченный частотой ![]() , то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени
, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени ![]() , т.е. с частотой
, т.е. с частотой ![]() .
.
Мы не приводим полную математическую формулировку теоремы, а также ее доказательство, а лишь ограничиваемся указанием сути теоремы. Однако, справедливость ее легко усматривается из рис. 10, б и 15, а. Частота дискретизации непрерывного сигнала не должна быть меньше удвоенной ширины спектра: ![]() иначе произойдет наложение спектров (рис. 15, б) и будет невозможно с помощью фильтра нижних частот выделить спектр исходного непрерывного сигнала.
иначе произойдет наложение спектров (рис. 15, б) и будет невозможно с помощью фильтра нижних частот выделить спектр исходного непрерывного сигнала.
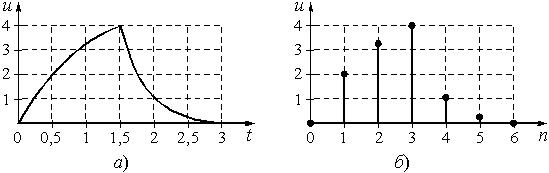
Рис. 16
Пример 7.1. Рассчитаем интервал дискретизации и минимально допустимую частоту дискретизации сигнала, спектральная плотность которого равна нулю при значениях частоты выше 100 кГц.
Из условия задачи следует, что граничная частота спектра ![]() равна 100 кГц. Тогда в соответствии с теоремой Котельникова имеем интервал дискретизации
равна 100 кГц. Тогда в соответствии с теоремой Котельникова имеем интервал дискретизации
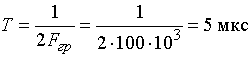 .
.
Минимально допустимая частота дискретизации ![]() = 2 ×× 100 = 200 кГц.
= 2 ×× 100 = 200 кГц.
Пример 7.2. Определим дискретные отсчеты сигнала длительностью ![]() = 3 мс, приведенного на рис. 16, а, если в качестве граничной частоты спектра
= 3 мс, приведенного на рис. 16, а, если в качестве граничной частоты спектра ![]() принять значение
принять значение ![]() , выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.
, выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.
Хотя сигнал конечной длительности имеет бесконечный спектр частот, однако почти всегда можно определить граничную частоту спектра таким образом, чтобы отсекание частот превышающих ![]() , привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.
, привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.
Граничная частота спектра 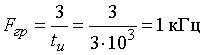 .
.
Интервал дискретизации 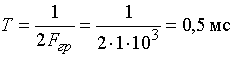 .
.
Берем отсчеты сигнала, приведенного на рис. 16, а, через интервал времени T = 0,5 мс и получаем последовательность![]() = {0; 2; 3,2; 4; 1; 0,3; 0}, изображенную графически на рис. 16, б.
= {0; 2; 3,2; 4; 1; 0,3; 0}, изображенную графически на рис. 16, б.
Самоконтроль
1. Как нужно выбирать интервал дискретизации сигнала, чтобы можно было однозначно восстановить непрерывный сигнал по его дискретным отсчетам?
2. Как выбирается минимальная частота дискретизации?
3. Найдите частоту дискретизации и интервал дискретизации сигнала, имеющего спектр, ограниченный частотой ![]() = 10 кГц.
= 10 кГц.
4. Уменьшите в 2 раза интервал дискретизации по сравнению с тем значением, которое получили в п. 3. Можно ли при этом однозначно восстановить непрерывный сигнал? Как изменится спектр сигнала?

