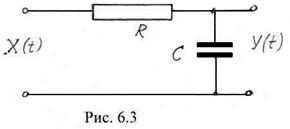
Рассмотрим задачу преобразования широкополосного случайного процесса вида «белого шума» со спектральной плотностью интегрирующей – цепью (рис. 6.3). Как известно, амплитудно – частотная характеристика цепи описывается выражением

,

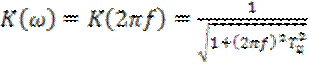где – постоянная времени цепи.

В первую очередь найдем шумовую полосу цепи. Воспользовавшись (6.16) при , получим

. (6.17)

Таким образом, шумовая полоса интегрирующей цепи конечна. Это вполне объяснимо, так как интегрирующая цепь является фильтром нижних частот.

Найдем характеристики процесса на выходе цепи, если на его вход поступает процесс с энергетическим спектром . Тогда, в соответствии с (6.9) энергетический спектр процесса на выходе цепи будет равен

. (6.18)

Автокорреляционная функция выходного процесса вычисляется в соответствии с (6.10)

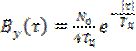. (6.19)

На рис. 6.4 изображены автокорреляционные функции и энергетические спектры входного и выходного случайных процессов. Из этих рисунков следует, что интегрирующая цепь вносит

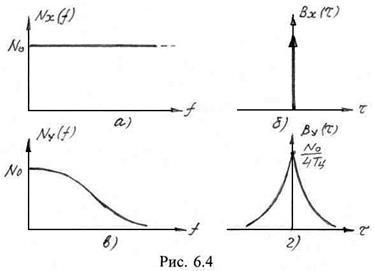корреляцию значений случайного процесса. Очевидно, дисперсия (средняя мощность) случайного процесса на выходе цепи

. (6.20)

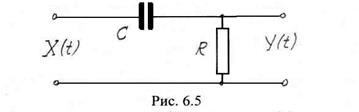Обратимся теперь к дифференцирующей – цепи (рис. 6.5).

Амплитудно – частотная характеристика цепи описывается выражением

.

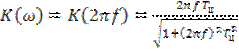При значение . Таким образом, дифференцирующая цепь является фильтром высоких частот и поэтому шумовая полоса цепи неограниченна. Действительно:

.

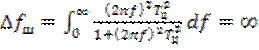Энергетический спектр СП на выходе дифференцирующей цепи:

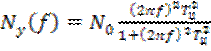. (6.21)

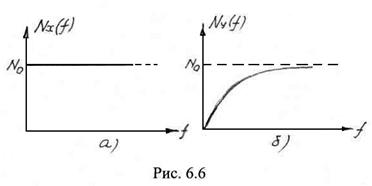На рис. 6.6 изображены энергетические спектры входного и выходного случайных процессов. Очевидно, дисперсия

.

Полученные результаты вполне объяснимы, т.к. дифференцирующая цепь по определению не относится к узкополосным цепям, т.к. для этой цепи .