Определим энергию сигнала f(t) по его спектральной характеристике F(jw). Предположим, что f(t) представляет собой напряжение или ток, протекающий в единичном сопротивлении R = 1 Ом. Тогда согласно (1.4) энергия выделяемая f(t) будет равна

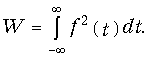
Представим подынтегральное выражение (9.35) в виде произведения 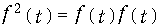и применим к f(t) обратное преобразование Фурье (9.7):

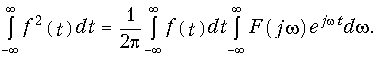
Учитывая независимость переменных t и w, перепишем последнюю формулу в виде

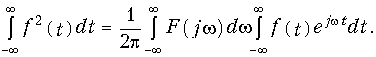
Внутренний интеграл представляет собой сопряженный спектр F(—jw). Если учесть, что 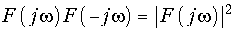, то получим следующее равенство Парсеваля (теорема Рэлея):

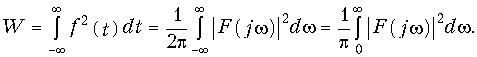
Из уравнения (9.36) следует, что величина |F(jw)|² представляет собой энергию сигнала, приходящуюся на 1 с^–1 текущей частоты w, поэтому квадрат модуля спектра |F(jw)|² называют спектральной плотностью энергии сигнала. Вид модуля |F(jw)| позволяет судить о распределении энергии в спектре непериодического сигнала. Равенство Парсеваля широко используется в теории цепей и сигналов при выборе полосы пропускания канала связи, обеспечивающей наилучшее использование энергии сигнала.

Следует отметить, что в отличие от формулы (5.23), где рассматривалась средняя за период Т мощность периодического несинусоидального сигнала, для непериодического сигнала такое усреднение невозможно ( 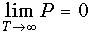). Общим для обеих случаев является то, что мощность и энергия сигналов не зависят от фаз спектральных составляющих.