5.5.1. Пассивные апериодические цепи
5.5.1. Пассивные апериодические цепи
При классификации радиотехнических цепей было отмечено, что по признаку наличия в цепи источника энергии цепи подразделяются на пассивные и активные. Начнем с рассмотрения пассивных цепей первого порядка, т.е. цепей содержащих один реактивный элемент (емкость или индуктивность). На основе этих цепей строятся как простейшие активные цепи, так и более сложные радиотехнические устройства.
Выше в качестве примера линейной цепи при рассмотрении методов анализа приводилась RC-цепь, которая получила название интегрирующей цепи. Рассмотрим еще одну RC-цепь, называемую дифференцирующей цепью, определим ее характеристики и сравним с характеристиками интегрирующей цепи.
Определение характеристик цепей можно проводить любым из рассмотренных выше методов. Так, например, при определении частотных характеристик цепей в данном случае удобно представить ту или иную цепь в виде делителя напряжения, в состав которого входят комплексные сопротивления 
и 
. Временные характеристики (переходную и импульсную) можно рассчитать как методом интеграла наложения, так и операторным методом.
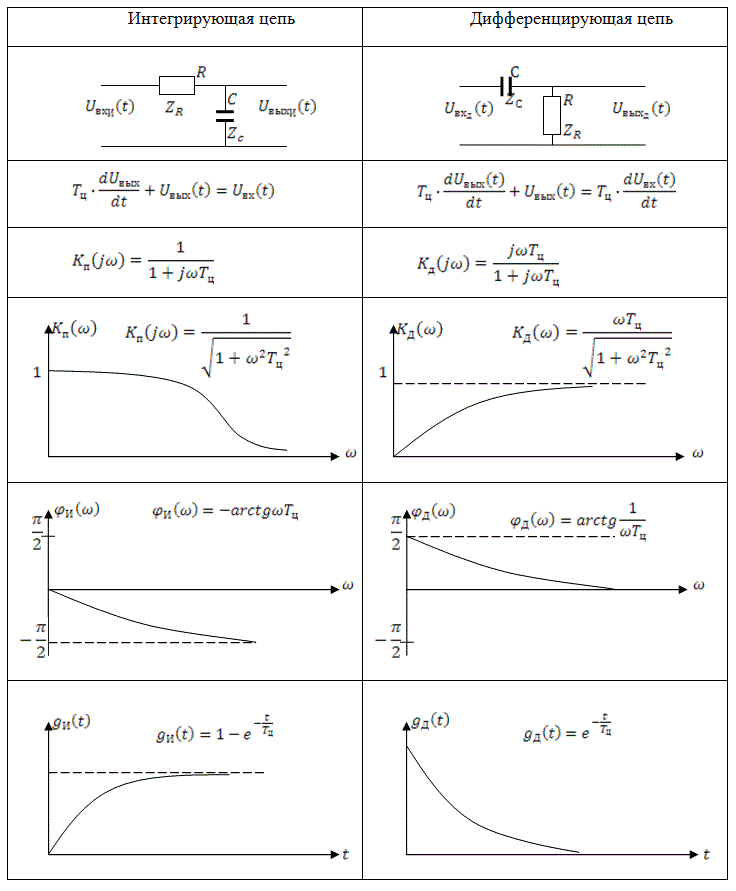
В таблице 5 представлены схемы интегрирующей и дифференцирующей цепи, дифференциальные уравнения, которыми описываются цепи, аналитические выражения комплексного коэффициента передачи 
, амплитудно-частотных 
, фазо-частотных 
, а также переходных 
и импульсных 
характеристик и их графические изображения.
Анализ графиков АЧХ цепей показывает, что интегрирующая цепь пропускает нижние частоты и задерживает верхние, т.е. является фильтром нижних частот (ФНЧ). Дифференцирующая цепь наоборот пропускает верхние частоты и тем самым является фильтром верхних частот (ФВЧ).
Форма временных (переходной и импульсной) характеристик определяет характер переходных процессов. Для рассматриваемых цепей переходные характеристики представляют собой монотонно возрастающую (для интегрирующей цепи) и монотонно убывающую (для дифференцирующей цепи) функции. Это определило название цепей как апериодических.
Обратимся к выражению для комплексного коэффициента передачи интегрирующей цепи. При 
комплексный коэффициент передачи
.
Так как входной и выходной сигналы связаны соотношением
,
то при указанном условии
. (5.40)
Но оператор 
является оператором интегрирования. Тогда применяя обратное преобразование Фурье, получим
,
т.е. цепь выполняет функцию интегрирования входного сигнала.
Аналогично для дифференцирующей цепи при 
и 
(5.41)
Таблица 5
Как известно, оператор 
– это оператор дифференцирования. Очевидно, обратное преобразование Фурье обеих частей (5.41) дает
.
Таким образом, рассмотренные простейшие RC-цепи осуществляют соответственно приближенное интегрирование и дифференцирование входных сигналов.
В заключение отметим, что в качестве интегрирующих и дифференцирующих цепей могут выступать и RL-цепи, где реактивными элементами являются индуктивности. Схемы этих цепей также представляют собой делители напряжения, с той лишь разницей, что в интегрирующей цепи выходной сигнал снимается с резистора, а в дифференцирующей – с индуктивности.
5.5.2. Пассивные частотно-избирательные цепи
К пассивным частотно-избирательным цепям относятся колебательные контуры. Простейший колебательный контур содержит резистор R, индуктивность L и емкость C. Если в контуре элементы R, L и C соединены последовательно, то такой контур называется последовательным, а если соединены параллельно – параллельным колебательным контуром.
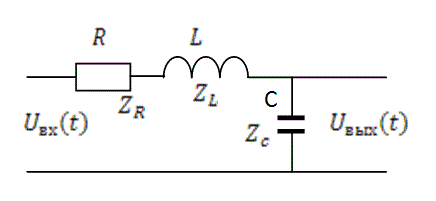
Рис.5.6
Один из вариантов последовательного колебательного контура изображен на рис. 5.6. Так же, как и предыдущие цепи, рассматриваемый контур можно представить как делитель напряжения. Тогда
комплексный коэффициент передачи контура
,
или с учетом того, что 
, 
и 
:
. (5.42)
Из этого выражения следует, что комплексный коэффициент передачи имеет максимум при
, (5.43)
т.е. последовательный колебательный контур из совокупности сигналов разных частот выделяет один, который имеет частоту 
. Это явление, как известно, называется резонансом, а частота 
– резонансной частотой.
Резонансная частота определяется из условия (5.43):
или 
. (5.44)
Рассмотрим основные характеристики последовательного колебательного контура.
Характеристическим сопротивлением называется значение сопротивления одного из реактивных элементов (индуктивности или емкости) при резонансной частоте
. (5.45)
Добротностью контура называется отношение характеристического сопротивления к резистивному
. (5.46)
Поясним физический смысл добротности. Из (5.42) при имеем
.
Тогда с учетом (5.46) можно записать
. (5.47)
Таким образом, добротность показывает во сколько раз напряжение на индуктивности или емкости (выходной сигнал) больше, чем приложенное входное напряжение. Затуханием контура называется безразмерная величина, обратная добротности
.
Постоянная времени контура
, (5.48)
характеризует инерционность контура. Очевидно, чем больше 
(чем больше 
), тем медленнее протекают переходные процессы в контуре.
Возвратимся к (5.42) и представим это выражение с учетом (5.44) в виде
.
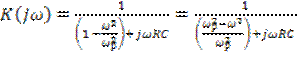Обозначая
,
после несложных преобразований получим
.
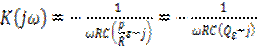Рассмотрим поведение комплексного коэффициента передачи в окрестности резонансной частоты, т.е. при 
. Тогда величина 
:
, (5.49)
где 
– абсолютная расстройка, представляет собой так называемую удвоенную относительную расстройку. С учетом этого выражение для комплексного коэффициента передачи можно представить как функцию удвоенной относительной расстройки в следующем виде
. (5.50)
Амплитудно-частотная характеристика
, (5.51)
а фазо-частотная характеристика
. (5.52)
На рис. 5.7 изображены графики АЧХ и ФЧХ рассматриваемого колебательного контура в окрестности резонансной частоты.
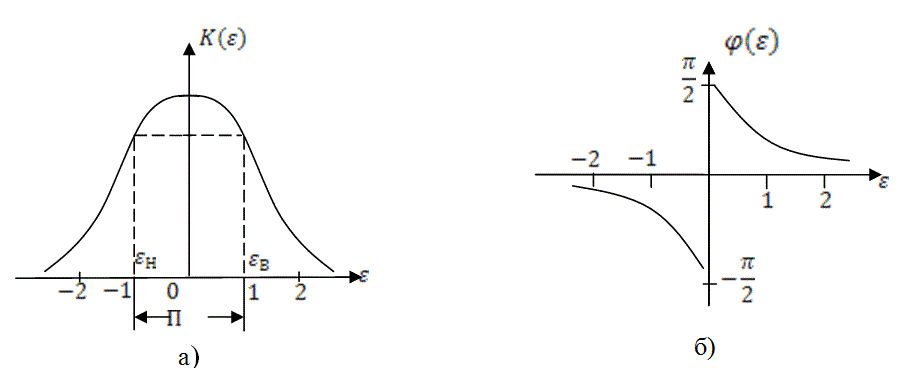
Рис. 5.7
Полосой пропускания контура называется диапазон частот, в пределах которого 
. Очевидно, равенство в этом выражении соответствует граничным частотам 
и 
полосы пропускания. Эти частоты находятся в результате решения уравнения
. (5.53)
Решение этого уравнения дает
, 
,
или с учетом (5.49)
, 
.
Тогда полоса пропускания контура определяется по формуле
. (5.54)
В заключение составим дифференциальное уравнение последовательного колебательного контура. Напряжение, приложенное к контуру:
, (5.55)
где 
– напряжение на резисторе, 
– напряжение на индуктивности, 
– напряжение на конденсаторе. Но напряжение на конденсаторе является выходным сигналом 
. С другой стороны напряжение на резисторе 
, а напряжение на индуктивности 
. Ток, протекающий через контур, можно выразить через напряжение на конденсаторе
.
Тогда напряжение на индуктивности
,
и на резисторе
.
Подстановка этих выражений в (5.55) дает соотношение
.
Разделим обе части этого уравнения на 
. Тогда уравнение принимает вид
, (5.56)
где 
– коэффициент затухания.
Применив к обеим частям уравнения (5.56) преобразование Лапласа, можно получить выражение для передаточной функции
. (5.57)
Нетрудно заметить, что замена в (5.57) 
на приводит к выражению (5.42).
Параллельный колебательный контур представляет собой параллельное соединение 
, 
и 
элементов (рис. 5.8). Входным сигналом такого контура является ток 
, а выходным – напряжение 
на элементах контура. Согласно закону Ома комплексное значение напряжения на элементах контура
.
В свою очередь комплексное сопротивление 
есть величина, обратная комплексной проводимости. При параллельном соединении 
, 
и 
комплексная проводимость равна
, (5.58)
или
. (5.59)
Проводя суммирование дробей, и вычисляя обратное значение суммы, получим
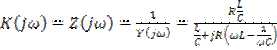. (5.60)
Как и в последовательном контуре, резонанс в параллельном колебательном контуре, как это следует из (5.60), имеет место при условии 
.
Характеристическое сопротивление контура описывается выражением (5.45). Что касается добротности 
, то в отличие от (5.46) для параллельного контура она определяется выражением
. (5.61)
Отсюда постоянная времени контура
. (5.62)
Вводя параметр 
и проводя аналогичные рассуждения, как и в случае последовательного контура, после несложных преобразований получим выражение для 
в окрестности резонансной частоты:
. (5.63)
Очевидно, амплитудно-частотная характеристика
, (5.64)
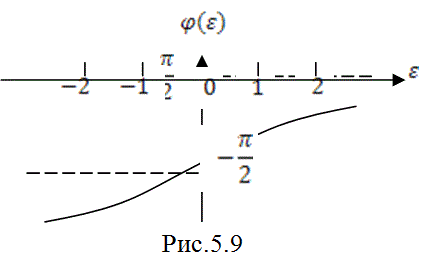
носит такой же характер, как и для последовательного контура (5.51). Поэтому график АЧХ параллельного контура совпадает по форме с кривой рис. 5.7а. Фазо-частотная характеристика имеет вид
. (5.65)
На рис. 5.9 приведен график ФЧХ параллельного контура. Полоса пропускания и граничные частоты 
и 
определяются аналогично этим же параметрами последовательного контура. При составлении дифференциального уравнения следует учесть, что входной сигнал – ток
, (5.66) где 
; 
; 
– токи, протекающие через соответствующие элементы, 
– напряжение на контуре, являющееся выходным сигналом 
.
Подстановка этих выражений в (5.65) дает
.
Дифференцирование левой и правой частей приводит к результату
, (5.67)
где 
– коэффициент затухания.
Передаточная функция параллельного контура описывается выражением
. (5.68)
5.5.3. Активные линейные цепи
Типичным примером активной цепи является усилитель, собранный на n-p-n транзисторе с общим эмиттером. Если нагрузкой усилителя служит R-цепь, то такой усилитель является апериодической активной цепью, а если нагрузкой служит колебательный контур – частотно-избирательной активной цепью.
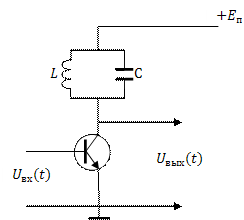
Рис. 5.10
На рис. 5.10 представлена упрощенная принципиальная схема частотно-избирательной активной цепи. При достаточно малой амплитуде входного сигнала такую цепь можно считать линейной (линейным усилителем малых сигналов). Этот случай мы и рассмотрим.
Для определения характеристик рассматриваемой активной цепи составим ее эквивалентную схему. Транзистор можно представить в
виде источника тока управляемого напряжением 
. Величина тока в этом случае составит
, (5.69)
где 
– крутизна характеристики транзистора (крутизна управления), имеющая размерность 
. Как известно, источник тока можно представить как параллельное соединение идеального источника и внутреннего сопротивления, в качестве которого выступает внутреннее сопротивление транзистора 
. Тогда эквивалентная схема рассматриваемой цепи принимает вид (рис. 5.11).
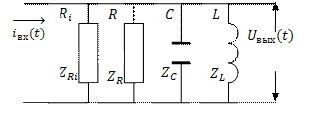
Рис.5.11
Так же, как и для пассивной цепи (параллельного контура) комплексный коэффициент передачи:
.
совпадает с комплексным сопротивлением 
. Вместе с тем, для рассматриваемой цепи комплексная проводимость определяется выражением
, (5.70)
где 
– эквивалентное сопротивление контура с учетом внутреннего сопротивления транзистора. Сравнение (5.70) с (5.59) показывает, что комплексный коэффициент передачи рассматриваемой цепи описывается выражением (5.60) с той лишь разницей, что вместо собственного сопротивления параллельного контура 
здесь выступает 
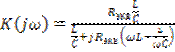. (5.71)
Очевидно, исходя из эквивалентной схемы, добротность рассматриваемого усилителя составит величину
. (5.72)
Так как 
, то включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности, что объясняется шунтирующим свойством транзистора.
Аналогично комплексный коэффициент передачи как функция удвоенной относительной расстройки ε описывается выражением
, (5.73)
а амплитудно-частотная и фазо-частотная характеристики – соответственно выражениями:
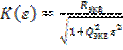, (5.74)
. (5.75)
Полоса пропускания рассматриваемого усилителя определяется в соответствии с (5.54), где вместо фигурирует 
. (5.76)
Очевидно, так как включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности до , это в свою очередь обуславливает расширение полосы пропускания.