8.1. Идеальная периодическая АКФ. Минимаксные бинарные последовательности
8.2. Начальные сведения о конечных полях и линейных последовательностях
8.3. Периодическая АКФ m–последовательностей
8.4. Дополнение о конечных полях
8.1. Идеальная периодическая АКФ. Минимаксные бинарные последовательности
Мотивация интереса к последовательностям с хорошей периодической АКФ не ограничивается лишь их привлекательностью как исходного материала для построения хороших апериодических последовательностей. Для многих приложений характерно использование дискретных сигналов в периодическом варианте (непрерывная локация, навигация, пилотные каналы мобильной связи и т.п.), что предопределяет критическое влияние свойств периодической АКФ (ПАКФ) на качество функционирования системы. Отметим также, что не существует никаких принципиальных ограничений к достижению нулевого уровня боковых лепестков ПАКФ ФМ сигналов, как это имело место в апериодической версии, поскольку в выражении
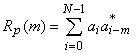
сумма при любом значении 
содержит 
слагаемых, которые потенциально могут скомпенсировать друг друга, обеспечивая нулевой результат. Тогда естественно стремление к отысканию ФМ кодовых последовательностей с идеальной ПАКФ, все боковые лепестки которой равны нулю
.
Дискретный видеосигнал с прямоугольными чипами, манипулированными кодом с подобными свойствами, также будет обладать идеальной ПАКФ: основные лепестки, повторяющиеся с периодом 
, и свободное от любых боковых лепестков пространство между ними (см. рисунок).
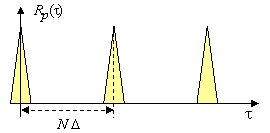
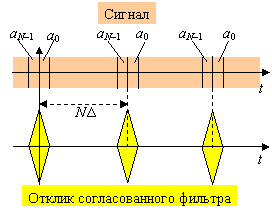
Аналогичным будет и отклик фильтра, согласованного с однопериодным сегментом сигнала. Следовательно, при идеальности ПАКФ имеет место идеальная (без боковых лепестков) временная компрессия сигнала согласованным фильтром. Иллюстрацией сказанному для радиосигнала служат диаграммы на рисунке.
Как и ранее, наиболее привлекательны в реализационном плане бинарные 
последовательности с идеальной ПАКФ. Простое необходимое условие существования бинарных кодов с идеальной ПАКФ может быть получено в результате суммирования значений ненормированной ПАКФ при всех возможных сдвигах :
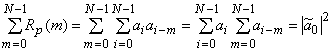
где знак комплексного сопряжения опущен за ненадобностью, поскольку все 
, а
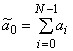
– постоянная составляющая (разность между числом «+1» и «–1» на одном периоде) кодовой последовательности 
. Поскольку последняя всегда принимает лишь целочисленные значения, а ПАКФ, как сумма «
», может принять нулевое значение только при четном числе слагаемых (длине кода) , то необходимое условие идеальности периодической АКФ для бинарной последовательности имеет вид
Все подобные длины были проанализированы Турином в начале 60-х, который показал, что в диапазоне 
единственным бинарным кодом с идеальной ПАКФ является тривиальный код длины 4 вида:{+1 +1 +1 –1}. Согласно более поздним результатам несуществование подобных последовательностей установлено вплоть до длин 
. Возможность их существования за пределами названного диапазона представляется крайне сомнительной.
Очевидно, что в отсутствие бинарных кодов с идеальной 
периодической АКФ следующими по привлекательности являются последовательности, для которых 
принимает значения при 
, т.е. 
. Рассмотрим разность
,
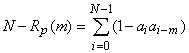в которой все ненулевые слагаемые равны двум, а их число всегда четно. Следовательно, указанная разность всегда кратна четырем
,
где t – целое.
Очевидно, можно надеяться на отыскание бинарных кодов со всеми положительными боковыми лепестками 
только при длинах вида 
и со всеми отрицательными 
при длинах 
, где 
– целое. Поскольку данные последовательности обладают теоретически минимальным уровнем боковых лепестков периодической АКФ 
для бинарных кодов нечетной длины, то их называют минимаксными.
Из двух возможных вариантов второй оказывается наиболее продуктивным. В настоящее время известно пять мощных регулярных правил генерирования минимаксных последовательностей с боковыми лепестками ПАКФ равными 
, два наиболее популярных из которых будут рассмотрены в дальнейшем.
8.2. Начальные сведения о конечных полях и линейных последовательностях
Для объяснения вышеупомянутых конструкций минимаксных бинарных последовательностей необходимо некоторое начальное представления о конечных полях. Назовем конечным полем (полем Галуа) конечное множество элементов, на котором определены две операции, именуемые (по аналогии с обычной арифметикой) сложением и умножением и обозначаемые привычными символами «+» и «∙». В любом поле обязательно присутствуют нулевой «0» и единичный «1» элементы, которые оставляют любой элемент поля неизменным в операциях сложения и умножения соответственно. Таблицы сложения и умножения в поле строятся таким образом, чтобы указанные операции были коммутативны, ассоциативны, дистрибутивны и обратимы. Последнее означает, что определены также операции вычитания и деления на ненулевой элемент. В частности, у каждого элемента имеется противоположный по сложению, а для любого ненулевого существует обратный по умножению элемент. Очевидно, что поле представляет собой множество, в пределах которого операции с элементами подобны операциям с действительными числами в обычной арифметике.
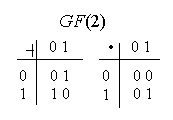
Простейшим конечным полем является поле порядка 2 (число элементов поля), обозначаемое как GF(2), элементы которого «0» и «1» подчиняются правилам арифметики по модулю 2 (см. таблицу слева).
Введем в рассмотрение последовательность 
с элементами (символами) 0 и 1 из конечного поля 
, подчиняющуюся линейной рекурсии:
где коэффициенты 
– фиксированные константы, принадлежащие . Элементы линейной последовательности вычисляются один за другим по правилам сложения и умножения в поле , причем каждый последующий определяется 
предшествующими, так что, задав начальных элементов 
, можно сгенерировать всю последовательность. Такая последовательность называется линейной (рекуррентной) последовательностью над полем памяти .
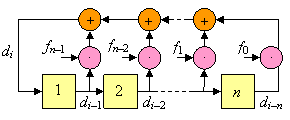
Любая линейная рекуррентная последовательность (ЛРП) может быть сформирована с помощью регистра сдвига с линейной обратной связью (РСЛОС), структурная схема которого представлена на рисунке справа. Регистр состоит из двоичных ячеек памяти (разрядов, триггеров), обозначенных квадратами, каждая из которых имеет 2 возможных состояния и хранит тот или иной элемент в течение тактового интервала. Схема тактовой синхронизации (на рисунке не показана) управляет работой регистра таким образом, что после каждого тактового импульса состояние любого разряда передается следующему слева направо. Схема обратной связи содержит умножители элементов (состояний), хранящихся в разрядах, на константы 
и сумматоров. Обе арифметические операции выполняются, разумеется, по правилам поля .
Предположим, что начальные состояния (т.е. начальные символы последовательности) 
записаны в разряды регистра слева направо. Тогда состояние выхода петли обратной связи определится равенством
и после подачи тактового импульса содержимое ячеек регистра сдвига примет вид 
, генерируя состояние обратной связи
,
так что после подачи тактового импульса состояние обратной связи будет 
и т.д. Обобщая, можно видеть, что в каждом такте текущее содержимое регистра 
формирует состояние обратной связи 
, которое является следующим символов ЛРП и входным сигналов для первой ячейки регистра сдвига. Таким образом, полностью линейная рекуррентная последовательность может быть непосредственно считана с крайнего правого разряда, начиная с самого первого символа 
, или с любого другого разряда, но с определенным опережением во времени.
Поскольку число различных состояний регистра конечно (не более 
), то любая линейная рекуррентная последовательность оказывается периодической (по крайней мере, после некоторого переходного процесса). Если регистр окажется в нулевом состоянии (нули во всех разрядах), все последующие символы будут также нулевыми, т.е. генерируемая линейная последовательность окажется вырожденной, состоящей только из нулей. Понятно, что подобная последовательность практически бессмысленна, так что нулевое состояние регистра в процессе генерирования последовательности должно быть исключено. В итоге остается самое большее 
разрешенных состояний регистра, означая, что максимальный период (длина) линейной последовательности не может быть больше .
Линейные рекуррентные последовательности, имеющие максимально возможный период
,
играют особую роль в современных информационных технологиях и называются последовательностями максимальной длины или просто m-последовательностями. Будучи полностью детерминированными, они обладают многими свойствами, присущими случайным последовательностям типа последовательности исходов подбрасывания правильной монеты, поэтому m–последовательности служат примером псевдошумовой последовательности. Два следующих замечательных свойства являются ключевыми для понимания ценности –последовательностей в плане построения кодов с хорошей автокорреляцией.
1. Свойство уравновешенности. На одном периоде –последовательности число единиц 
всегда превышает число нулей 
ровно на единицу
.
2. Свойство сдвига и сложения. Поэлементное сложение (разумеется, по модулю 
) некоторой -последовательности и ее копии, циклически сдвинутой на позиций, дает нулевую последовательность, если взаимный сдвиг m кратен периоду N:
– целое,
либо некоторую новую сдвинутую (на l позиций) копию исходной -последовательности в противном случае:
.
8.3. Периодическая АКФ m–последовательностей
Причиной особого интереса к m–последовательностям служат их хорошие автокорреляционные свойства. Преобразуем –последовательность в бинарный код 
посредством отображения по следующему правилу
.
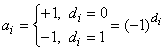Полученная таким образом последовательность действительных бинарных символов также назовем бинарной -последовательности. Для устранения риска перепутывания можно при необходимости использовать дополнительную маркировку типа «бинарная 
последовательность» или «бинарная 
последовательность». Отличительной особенностью бинарных -последовательностей служит принадлежность их к числу минимаксных
.
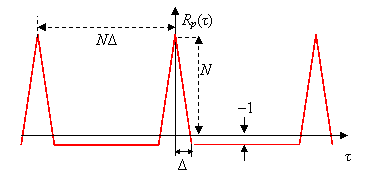
Теперь становится очевидным, что дискретный видеосигнал, манипулированный подобного рода бинарным кодом, будет обладать периодической АКФ, представленной на рисунке слева: главные пики уровня , повторяющиеся с периодом 
и равномерный фон отрицательных боковых лепестков на уровне .
Для генерирования -последовательности с помощью регистра сдвига памяти необходимо и достаточно использовать в рекурсии (или РСЛОС) множители 
, являющиеся коэффициентами специального полинома степени n
,
называемого примитивным полиномом. Примитивные полиномы существуют для любого натурального , обеспечивая тем самым существование минимаксных бинарных кодов на основе – последовательности любого периода вида
Примитивные полиномы подробно табулированы в ряде руководств по современной алгебре и теории кодирования, а также в некоторых книгах по широкополосной связи.
Пример 8.3.1. Пусть 
. Из таблиц найдем примитивный полином третьей степени:
,
определяющий коэффициенты линейной рекурсии 
:
и структуру РСЛОС генератора на рисунке ниже.
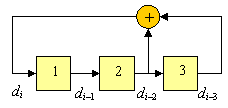
При начальном состоянии регистра 
порождается m–последовательность 
периода 
.
Легко увидеть, что на одном периоде последовательности число единиц 
на единицу превосходит число нулей 
. Посимвольное сложение исходной последовательности 
с ее сдвинутой на одну позицию влево копией дает последовательность, которая является копией исходной, но с другим циклическим сдвигом. Иначе говоря, 
. И наконец, прямая проверка (достаточно проверить только при сдвигах 
) показывает, что периодическая АКФ бинарного кода 
принимает значения
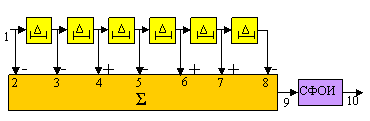
Структура фильтра, согласованного с одним периодом сигнала, манипулированного полученным бинарным кодом, представлена на рисунке справа. Эпюры напряжений в характерных точках показаны на рисунке ниже. Можно видеть, что выходной отклик содержит главные пики треугольной формы, повторяющиеся с периодом , и равномерный фон отрицательных боковых лепестков, уровень которых в семь раз меньше уровня главных пиков.
Дискретные сигналы, основанные на бинарных -последовательностях чрезвычайно популярны в современных информационных системах, благодаря оптимальным периодическим корреляционным свойствам и простоте формирования и обработки. В то же время, множество длин, при которых данные последовательности существуют, достаточно разрежено. По этой причине целесообразно исследовать еще один интересный класс бинарных минимаксных последовательностей.
8.4. Дополнение о конечных полях
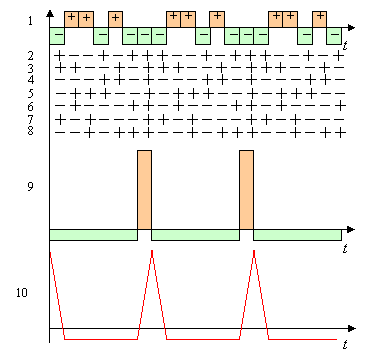
Расширим немного наши знания о конечных полях. Аналогично арифметике по модулю два можно использовать правила сложения и умножения по модулю числа 
, удерживая после обычных операций сложения и умножения целых чисел только остаток от деления результата на целое . Если является простым числом, то эти операции порождают конечное поле 
порядка (т.е. содержит элементов), называемое простым полем.
Пример 8.4.1. Взяв 
и составив таблицы сложения и умножения (см. таблицу справа), содержащие остатки от деления на 5, приходим к операциям, обладающим всеми характерными свойствами поля: эти операции удовлетворяют законам коммутативности, ассоциативности и дистрибутивности. Кроме того, присутствует нулевой (не изменяющий результата сложения) и единичный (не изменяющий результата умножения) элементы. Данные операции являются обратимыми: любому элементу 
можно сопоставить обратный элемент по сложению 
, такой что 
, а для любого ненулевого элемента существует обратный элемент по умножению 
. В то же время не существует поля с арифметикой по модулю 4: элемент 
не имеет обратного по умножению элемента, поскольку обычное произведение любого целого на 2 дает четное число, остаток от деления которого на 4 также будет четным.
В любом поле автоматически присутствуют степени любого элемента с обычными правилами обращения с ними:
.
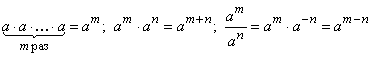Однако в отличие от поля вещественных чисел, в конечном поле имеется конечное число различных степеней элемента , поскольку общее число элементов поля конечно. Специфический элемент 
поля , степени которого пробегают все ненулевые элементы поля называется примитивным. Следовательно, все степени примитивного элемента вида: 
различны и совпадают с некоторым ненулевым элементом поля. Можно доказать, что в любом конечном поле существует (не единственный) примитивный элемент.
Пример 8.4.1. (продолжение) Элемент 2 в поле 
является примитивным, поскольку его 
степеней 
, 
, 
, 
, 
, … различны и, как видно, исчерпывают все ненулевые элементы поля . С другой стороны, элемент 4 не является примитивным, т. к. 
, 
, 
и элементы 2 и 3 не являются некоторой степенью 4.
Поскольку любой ненулевой элемент поля есть некоторая степень примитивного элемента 
, то вполне естественно назвать показатель этой степени логарифмом элемента по основанию :
.
Двузначным характером (символом Лежандра) 
ненулевого элемента поля называется функция, принимающая значения 
и в зависимости от четности или нечетности логарифма элемента :
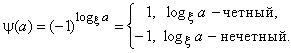
В дальнейшем понадобятся следующие свойства двузначного характера.
1. Характер единицы поля равен единице: 
.
2. Характер – мультипликативная функция, иными словами, характер произведения ненулевых элементов есть произведение их характеров: 
.
3. Свойство уравновешенности: сумма характеров всех ненулевых элементов поля равна нулю: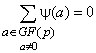 
.
4. Характер элемента, противоположного единице, т.е. 
принимает значения :
8.5. Последовательности Лежандра
Бинарные последовательности Лежандра формируются на основе двузначного характера. Возьмем простое и построим простое поле . Отождествим его элементы 
с номерами позиций 
символов 
периодической бинарной последовательности 
периода 
. Тогда для периодической версии последовательности Лежандра правило формирования определяется в виде
Используя свойства двузначного характера, достаточно просто доказать, что ПАКФ последовательности Лежандра длины 
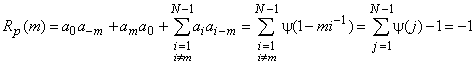
для любого 
, т.е. в точности совпадает с ПАКФ m–последовательности
.
Следует отметить, что присвоение первому элементу последовательности значения –1 приведет к тому же конечному результату.
Пример 8.5.1. Длина 
принадлежит множеству вида 
. В поле 
элемент 
является примитивным, поскольку возведение его в степень 0, 1, …, 5 генерирует все различные ненулевые элементы : 
. Как прямо видно из этого ряда, логарифмы элементов 1, 2, и 4 четны, тогда как элементов 3, 5 и 6 – нечетны. Следовательно, 
, и 
. Расстановка символов +1 на позициях 
и –1 на позициях 
дает последовательность Лежандра:
.
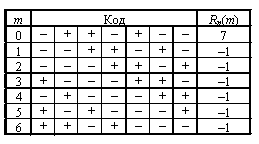
Вычисления, поясняемые таблицей слева, подтверждают, что все боковые лепестки ПАКФ данной последовательности, равны –1.
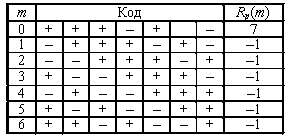
Последовательности Лежандра образуют достаточно мощный класс бинарных кодов с минимаксной периодической АКФ. Так например, в диапазоне от 50 до 1500 имеется только пять длин, для которых существуют -последовательности, тогда как для последовательностей Лежандра это количество равно 114.
8.6. Вновь о бинарных кодах с хорошими апериодическими АКФ
Сведения, накопленные о бинарных последовательностях с хорошими периодическими АКФ, дают теперь возможность вернуться к идее, состоящей в использовании таких последовательностей в качестве исходного материала для поиска кодов с нужными свойствами апериодических автокорреляций. Как было показано ранее, хорошими апериодическими свойствами могут обладать только последовательности с хорошими периодическими корреляционными свойствами.
Рассмотрим некоторую кодовую последовательность 
длины . Любой ее циклический сдвиг 
, имеет ту же периодическую АКФ, что и исходный код, так как периодическая АКФ инвариантна к циклическому сдвигу. Апериодическая же АКФ циклически сдвинутой копии может отличаться от АКФ первоначальной последовательности. Данный факт служит основой широко распространенного алгоритма поиска кодов с приемлемой апериодической АКФ, описанного ниже.
1). Для требуемой длины тем или иным способом отбирается некоторое множество последовательностей-кандидатов, имеющих хорошие периодические АКФ. Пусть, например, их число равно 
.
2). На втором этапе осуществляется полный перебор по критерию минимума максимального бокового лепестка апериодической АКФ среди всех однопериодных сегментов последовательностей-кандидатов. Очевидно, что всего необходимо произвести 
тестовых проверок.
3). Итогом поиска является один или несколько сегментов одной или нескольких последовательностей, имеющий минимальное значение 
среди всех последовательностей, отобранных на первом этапе. Разумеется, нет никаких гарантий глобальной оптимальности полученного кода среди всех возможных бинарных последовательностей данной длины.
Пример 8.6.1. Для длины 
, удовлетворяющей условию существования -последовательности, имеются два примитивных бинарных полинома степени 3: 
и 
. Непосредственная проверка показывает, что -последовательности, генерируемые ими, зеркальны друг другу, т.е. одна из них получается чтением другой справа налево. К подобному преобразованию инвариантны и периодическая, и апериодическая АКФ, поэтому в множество кандидатов достаточно включить только одну -последовательность, скажем, из примера 8.3.1: 
. Кроме того, является простым числом вида , т.е. последовательность Лежандра данной длины также существует, а именно последовательность примера 8.5.1: 
, к которой можно добавить ее модификацию с первым символом, замененным на –1. Последняя полностью повторяет отобранную -последовательность, тогда как первая – после замены знаков всех элементов – совпадает с циклически сдвинутой отброшенной -последовательностью. Поскольку изменение полярности вновь не влияет на периодическую и апериодическую АКФ, лишь одна из четырех рассмотренных минимаксных последовательностей достаточна для включения в множество кандидатов. Пусть ею будет последовательность Лежандра, начинающаяся символом +1.
Вычисление ее апериодической АКФ дает следующие значения 
, и 
. После циклического сдвига на одну позицию влево приходим к последовательности 
, для которой 
, 
, т.е. максимальный апериодический боковой лепесток хуже, чем у исходной. Следующий циклический сдвиг дает 
и 
, , т.е. не улучшает первоначальный результат. После следующего сдвига приходим к последовательности 
, имеющей апериодическую АКФ с боковыми лепестками 
, т.е. с 
. Данная последовательность является глобально оптимальной среди всех ФМ кодов, поскольку ни один из таковых не может обладать меньшим максимальным апериодическим боковым лепестком. В действительности, найден бинарный код Баркера длины 7.
На основании описанной выше процедуры было найдено множество бинарных кодов с приемлемыми свойствами апериодической АКФ длин вплоть до тысяч, уровень боковых лепестков которых хорошо аппроксимируется соотношением
.
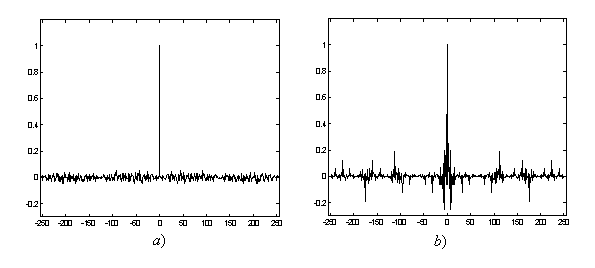
Для иллюстрации продуктивности данного метода на рисунке следующего слайда представлены апериодические АКФ двух бинарных кодов длины 
. Первый (a) получен в результате укорочения последовательности Лежандра длины 
и последующей оптимизации его циклических сдвигов, как описывалось ранее. Как видно, боковые лепестки данной АКФ имеют достаточно низкий уровень 
или 
дБ. Для сравнения на рисунке (b) представлена АКФ кода, используемого в 3G системе мобильной связи стандарта WCDMA для первичной синхронизации (поиска сот), который обладает большим уровнем боковых лепестков 
или 
дБ. Конечно, необходимо иметь в виду, что при выборе кода для поиска соты в WCDMA приходилось считаться со многими факторами, включая реализационные, которые могли оказаться важнее хорошей автокорреляции.