2.1. Условия самовозбуждения

2.2. Устойчивость амплитуды автоколебаний

2.2.1. Мягкое самовозбуждение

2.2.2. Жесткое самовозбуждение

2.3. Устойчивость фазы (частоты)

2.4. Схемы автогенераторов

2.4.1. Простые трехточечные схемы

2.4.2. Сложные трехточечные схемы

2.5. Стабилизация частоты автогенератора

2.5.1. Основные причины изменения частоты автогенератора

2.5.2. Дестабилизирующие факторы и методы борьбы с ними

2.5.3. Схема Шембеля

2.6. Особенности автогенераторов на транзисторах

2.7. Кварцевая стабилизация частоты

2.7.1. Электрическая эквивалентная схема кварца

2.7.2. Схемы кварцевых генераторов

2.7.3. Кварцевая стабилизация частоты в диапазоне волн

Частота и стабильность колебаний, излучаемых радиопередатчиком, определяются его возбудителем. Современные возбудители представляют собой сложные электронные устройства. Важнейшим элементом их структурной схемы является генератор с самовозбуждением (автогенератор), который представляет собой автономную электрическую систему, предназначенную для создания высокостабильных колебаний высокой частоты.

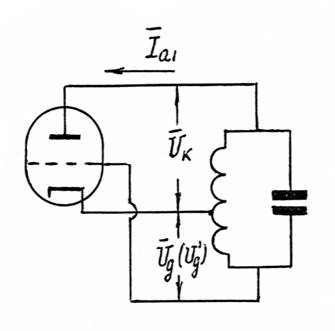
Рис.2.1

В радиопередатчиках используются, главным образом, одноконтурные автогенераторы, построенные по трехточечным схемам, в которых колебательный контур подключается к лампе (или транзистору) тремя точками. В качестве примера может быть рассмотрен одноконтурный автогенератор с автотрансформаторной обратной связью (рис. 2.1). При анализе амплитудных и фазовых соотношений в автогенераторе в установившемся режиме, а также при рассмотрении условий устойчивости амплитуды и фазы автоколебаний, можно воспользоваться квазилинейной теорией Берга, когда характеристику анодного тока лампы аппроксимируют отрезками прямых. При этом, как было показано выше, ламповый генератор может быть представлен эквивалентной схемой рис. 1.8, справедливой для общего случая работы генератора - на комплексную нагрузку в перенапряженном режиме, когда приведенное внутреннее сопротивление лампы - комплексная величина , зависящая от угла отсечки анодного тока q и от электронного режима генераторной лампы.

2.1. Условия самовозбуждения

Амплитуда и частота установившихся колебаний в автогенераторе определяются условием самовозбуждения:

(2.1)

Здесь - приведенный коэффициент обратной связи :

, (2.2)

где - коэффициент обратной связи, который показывает, какая часть напряжения на контуре подается на управляющую сетку (- напряжение обратной связи - см. рис.2.1 ); -средняя крутизна лампы , которая , как было показано при анализе эквивалентной схемы генератора, равна (1.15) , и так же , как и приведенное внутреннее сопротивление ,зависит от угла отсечки анодного тока лампы и от её электронного режима .

Условие самовозбуждения в комплексной форме (2.1) можно представить в виде двух уравнений :

(2.3)

и

, (2.4)

где m - целое число, или 0.

Выражение (2.3) носит название уравнения баланса (или равновесия) амплитуд в автогенераторе и определяет амплитуду установившихся колебаний. Выражение (2.4) называется уравнением баланса фаз в автогенераторе и определяет частоту установившихся колебаний. Здесь - фазовый угол эквивалентного сопротивления контура:, это угол между первой гармоникой анодного тока лампы и напряжением на контуре , он зависит от частоты, т.к. представляет собой фазовую характеристику параллельного колебательного контура; - фазовый угол средней крутизны - угол между первой гармоникой анодного и управляющим напряжением ,поскольку ;- фазовый угол приведенного коэффициента обратной связи - угол между управляющим напряжением и напряжением на контуре , так как

.

Углы и φ_к’ зависят, главным образом, от режима работы лампового генератора, то есть от питающих лампу напряжений и величины её нагрузки. При СВЧ на величину этих углов влияет инерция электронов. На угол φ_s оказывают влияние также высшие гармоники в сеточной цепи автогенератора.

Присутствие в уравнении баланса амплитуд множителя , зависящего от угла отсечки анодного тока лампы и от режима её работы , позволяет установить причину ограничения нарастания амплитуды колебаний в автогенераторе. В самом деле, из уравнений (2.3) и (2.2) получим, что коэффициент обратной связи равен:

, (2.5)

где определяется выражением (1.16).

Как мы видели, при угле отсечки q > 90° нарастание амплитуды приводит к уменьшению угла отсечки; когда q < 90° при нарастании амплитуды угол отсечки увеличивается. Если рабочая точка выбрана на прямолинейном участке характеристики лампы, то есть q > 90°, и обратная связь больше значения, определяемого (2.5) :

>) ,

то амплитуда колебаний будет увеличиваться. При этом угол отсечки будет уменьшаться, коэффициент приведения -расти (см.рис.1.6а), а значит будет расти и приведенное внутреннее сопротивление лампы . Это продолжится до тех пор, пока не восстановится равенство (2.5). Увеличение внутреннего сопротивления при возрастании анодного тока происходит ещё и потому, что при этом увеличивается сеточный ток, а значит возрастает коэффициент . Таким образом, стабилизация амплитуды автоколебаний обусловлена нелинейностью внутреннего сопротивления лампы и зависимостью его величины от её электронного режима.

2.2. Устойчивость амплитуды автоколебаний

Выполнение уравнений баланса амплитуд и баланса фаз являются необходимыми, но недостаточными условиями для длительного существования колебаний в автогенераторе, которое возможно лишь при выполнении условий устойчивости амплитуды и фазы.

Условие устойчивости амплитуды автоколебаний выражается неравенством

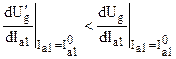, (2.6)

которое означает, что для устойчивого состояния равновесия необходимо, чтобы при любом случайном приращении DU_g напряжения возбуждения приращение анодного тока D при = приводило к приращению напряжения обратной связи D, которое было бы меньше приращения напряжения D, то есть необходимо, чтобы выполнялось неравенство . Условие устойчивости амплитуды (2.6) удобно представить в виде неравенства

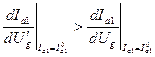, ( 2.6’)

которое означает, что в точке, соответствующей устойчивому состояний равновесия, тангенс угла наклона линии обратной связи больше тангенса угла наклона колебательной характеристики.

Условие устойчивости амплитуды можно представить также в виде неравенства:

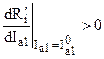, (2.7)

которое имеет ясный физический смысл: амплитуда автоколебаний устойчива при условии, что при её увеличении увеличивается и приведенное внутреннее сопротивление лампы, что препятствует нарастанию амплитуды колебаний; при уменьшении амплитуды колебаний приведенное внутреннее сопротивление уменьшается, что приводит к нарастанию амплитуды. Таким образом, приведённое внутреннее сопротивление является тем элементом, который определяет устойчивость амплитуды автоколебаний.

При анализе условий самовозбуждения колебаний и устойчивости их амплитуды весьма наглядным является графический метод, при котором рассматриваются колебательные характеристики и прямые обратной связи автогенератора, работающего в заданном режиме.

Прямая обратной связи представляет собой зависимость возникшего на контуре напряжения обратной связи от анодного тока лампы : =КU_к . Однако, обычно прямая обратной связи выражается уравнением

(2.8)

(предполагается, что нагрузка настроена и режим недонапряженный (то есть U_к =I_а1R_э). Эта зависимость представляет собой прямую линию, выходящую из начала координат и имеющую тем больший наклон, чем больше коэффициент обратной связи К.

Колебательная характеристика представляет собой зависимость первой гармоники анодного тока от напряжения возбуждения и определяется выражением:

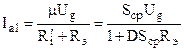(2.9)

Форма колебательной характеристики, как мы видели (см.п.1.1.7), зависит от исходной рабочей точки на статических характеристиках анодного тока, то есть от угла отсечки анодного тока q: при угле отсечки q > 90° колебательная характеристика имеет вид выпуклой кривой без точек перегиба (рис.1.9б). При угле отсечки q < 90° колебательная характеристика при малых амплитудах напряжения возбуждения вогнута, затем кривая имеет точку перегиба и в дальнейшем приобретает выпуклость (рис.1.9в).

При использовании в автогенераторе фиксированного смещения на управляющей сетке характер самовозбуждения зависит от положения рабочей точки на характеристике лампы: при (q>90⁰) самовозбуждение носит название мягкого; при (q < 90°) - жесткого (здесь - напряжение запирания).

2.2.1. Мягкое самовозбуждение

На графике рис.2.2а изображены колебательная характеристика автогенератора при угле отсечки анодного тока q>90⁰ и несколько прямых обратной связи, соответствующих различным значениям коэффициента обратной связи K. При малых значениях К ( К₁ < К₂) колебательная характеристика имеет только одну точку пересечения с прямой обратной связи. Эта точка соответствует состоянию покоя . Из рис.2.2а видно, что в данном случае состояние покоя является устойчивым, так как крутизна прямой обратной связи здесь больше крутизны колебательной характеристики. С увеличением коэффициента обратной связи при некотором его значении прямая обратной связи будет иметь уже две точки пересечения с колебательной характеристикой - 0 и А . Теперь в точке 0 крутизна линии обратной связи становится меньше крутизны колебательной характеристики, эта точка становится неустойчивой, и возникают автоколебания, амплитуда которых нарастает до второй точки пересечения А, которая является устойчивой. При дальнейшем увеличении коэффициента обратной связи точка пересечения перемещается вправо, и вместе с этим изменяется амплитуда генерируемых колебаний.

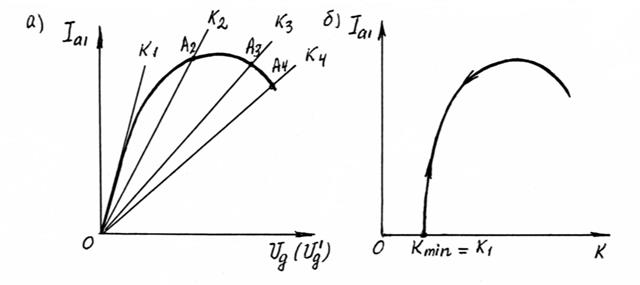
Рис.2.2

Кривая зависимости тока первой гармоники анодного тока I_a1 от коэффициента обратной связи К показана на рис.2. 2б.

Рассмотренный характер самовозбуждения лампового генератора называется мягким самовозбуждением, так как при достаточном коэффициенте обратной связи колебания нарастают самопроизвольно, без внешних толчков. Автоколебания возникают и срываются при одном и том же минимальном значении коэффициента обратной связи К _min , который определяется из (2.5) и равен 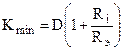, поскольку . Очевидно, самовозбуждение генератора возможно при коэффициенте обратной связи .

2.2.2. Жесткое самовозбуждение

При q < 90° самовозбуждение колебаний имеет иной характер. На рис.2.3а показаны колебательная характеристика и несколько прямых обратной связи, которые соответствуют разным значениям коэффициента обратной связи К. При К<К₄ точка покоя () является устойчивой и, следовательно, без внешнего толчка caмовозбуждение невозможно. При К=К₄ состояние покоя схемы становится неустойчивым, вследствие чего возникают колебания, амплитуда которых нарастает до значения, соответствующего точке пересечения А₄, которая является устойчивой. Если теперь уменьшать обратную связь, колебания прекратятся только при коэффициенте обратной связи К£K₁. Кривая изменения амплитуды колебаний в функции от коэффициента обратной связи имеет характерную петлю (рис.2.3б). Для возбуждения автоколебаний при коэффициенте обратной связи К₁ < К< К₄ необходим первоначальный толчок, при котором напряжение на управляющей сетке превышает значение, так как ему соответствует точка пересечения В, являющаяся неустойчивой. При амплитуда колебаний нарастает до значения, соответствующего точке пересечения А₂, которая является устойчивой. При колебания затухают.

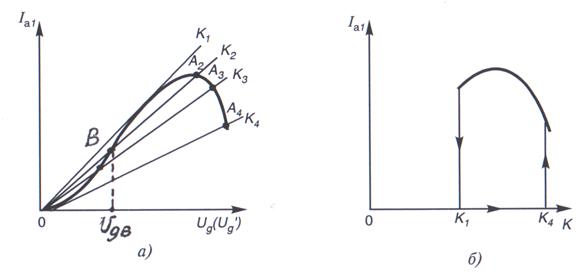
Рис.2.3

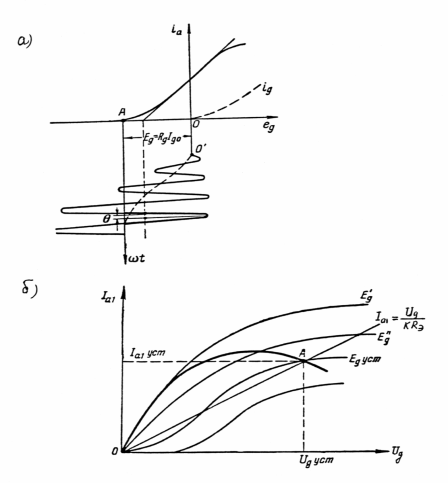
Рис.2.4

Применение в автогенераторах автоматического смещения за счет сеточного тока позволяет получить мягкое самовозбуждение при углах отсечки в установившемся режиме меньше 90⁰. При включении автогенератора, когда амплитуда автоколебаний равна нулю, сеточный ток отсутствует и, следовательно, напряжение смещения на управляющей сетке лампы равно нулю, то есть угол отсечки равен 180 ⁰ и происходит мягкое самовозбуждение. При возрастании амплитуды автоколебаний появляется и растёт сеточный ток, поэтому увеличивается отрицательное смещение на сетке (рис.2.4а), угол отсечки анодного тока q уменьшается, и рабочая точка переходит с колебательной характеристики, соответствующей большему значению q на характеристику с меньшим q , пока не достигнет устойчивой точки (А) при заданном коэффициенте обратной связи К (рис.2.4б). Сопротивление автоматического смещения R_g может быть выбрано так, чтобы угол отсечки q в установившемся режиме был меньше 90⁰. Для того, чтобы не возникла прерывистая генерация необходимо соблюдение неравенства R_gC_g£50T, где C_g - ёмкость конденсатора цепи автоматического смещения, Т - период автоколебаний (в автогенераторах на транзисторах требуется, чтобы R_эC_э £ , где R_э и C_э - элементы цепи автоматического смещения в цепи эмиттера, Q – добротность колебательного контура автогенератора).

2.3. Устойчивость фазы (частоты)

Условие баланса фаз в автогенераторе, как было показано выше, определяется выражением:

j_э + j_s + j_к =0 (2mπ) (2.4)

Поскольку фазовые углы j_s и j_к малы и при малых изменениях частоты меняются очень мало, то для простоты рассуждений при рассмотрении устойчивости фазы можно принять их равными нулю. Тогда условие баланса фаз примет вид:

j_э =0 . ( 2.4’)

При этом частота автоколебаний в стационарном режиме равна резонансной частоте контура.

Фаза (частота) автоколебаний будет устойчива в том случае, когда при малом случайном изменении частоты w фазовый угол j_э будет изменяться так, чтобы частота автоколебаний возвратилась к своему значению при состоянии равновесия фаз.

Можно показать, что устойчивость фазы (частоты) автогенератора обеспечивается его колебательным контуром. Математически условие устойчивости фазы (частоты) автогенератора выражается формулой:

<0 (2.10)

Это можно пояснить следующим образом. При изменении частоты, например, при w < w_раб,первая гармоника анодного тока будет отставать от напряжения на контуре (рис.2.5). Однако, из рис.2.5 видно, что напряжение обратной связи , синфазное с напряжением на контуре , опережает напряжение, поэтому фазовый сдвиг между и будет уменьшаться.

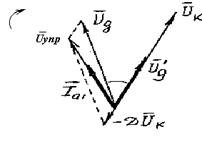
Рис 2.5.

Итак, устойчивость амплитуды колебаний в автогенераторе определяется лампой (нелинейным характером её внутреннего сопротивления и зависимостью его величины от электронного режима лампы), а устойчивость их частоты (фазы) - колебательным контуром.

2.4. Схемы автогенераторов

2.4.1. Простые трехточечные схемы

Большинство схем автогенераторов можно представить в виде обобщенной трёхточечной схемы, в которой колебательный контур подключён к лампе (транзистору) тремя точками (рис.2.6а). Пренебрегая влиянием инерции электронов, высших гармоник и сеточного тока, уравнение баланса фаз можно выразить равенством ( 2.4’):

j_э =0.

Это означает, что контур настроен на частоту автоколебаний, то есть, согласно рис.2.6а:

X _ag + X _gк + X _ак =0.

Как мы видели, коэффициент обратной связи К=, где - напряжение обратной связи, снимаемое с части контура (рис.2.1). При резонансе токи в ветвях контура одинаковы, поэтому коэффициент обратной связи K можно представить в виде:

К=

(здесь I_a1Q=I_к - контурный ток). Поскольку напряжение обратной связи и напряжение на контуре синфазны, то реактивные сопротивления X _ак и X_gк должны быть одного знака, при этом сопротивление X_ag должно быть противоположного знака. В качестве примера на рис.2.6б и 2.6в изображены схемы ёмкостной и индуктивной трёхточечных схем. Эти схемы получили название простых трёхточек.

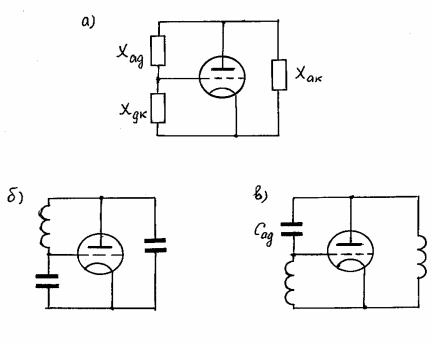
Рис 2.6.

2.4.2. Сложные трехточечные схемы

На УКВ используют сложные трёхточечные схемы, в которых реактивное сопротивление X_ag образовано проходной ёмкостью лампы С_ag , а сопротивления X_ак и X_gк, которые должны иметь индуктивный характер, - расстроенными контурами, включёнными между анодом и катодом (наружный контур) и между сеткой и катодом (внутренний контур) (рис.2.7).

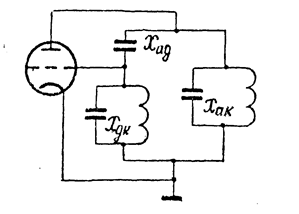
Рис.2.7

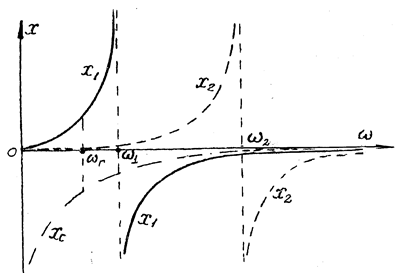
Рис.2.8

Нагрузочная цепь, с которой связан анодный контур генератора, обычно непостоянна во времени, поэтому собственная частота анодного контура w_ак (с учётом вносимой в него из нагрузочной цепи реактивности) может изменяться. Из рис 2.8 видно, что генерируемая частота w_г ближе к собственной частоте того контура, который настроен на более низкую частоту. Поэтому для ослабления влияния нагрузки на частоту автоколебаний собственная частота анодного контура должна быть выше, чем у сеточного, тогда генерируемая частота будет определяться главным образом параметрами сеточного контура. Если анодный контур сильно расстроен относительно сеточного, то мощность, отдаваемая в нагрузочную цепь, понизится, но при этом непостоянство параметров анодного контура мало отразится на генерируемой частоте. Эту особенность схемы используют для повышения стабильности частоты автоколебаний. Обычно частота анодного контура приблизительно в полтора раза больше, чем сеточного.

2.5. Стабилизация частоты автогенератора

Стабильность частоты является одним из важнейших электрических показателей радиопередатчика. Ею в значительной степени определяется надежность работы радиолиний. Требования к стабильности частоты современных радиопередатчиков очень высоки - порядка 10^-6 - 10^-7 , а для однополосной связи и синхронного радиовещания - порядка 10^-9 . Как указывалось выше, стабильность частоты передатчика определяется главным образом задающим генератором.

2.5.1. Основные причины изменения частоты автогенератора

Частота колебаний автогенератора определяется уравнением баланса фаз (2.4). Поскольку фазовые углы j _s и j _к в весьма слабой степени зависят от частоты , можно принять их независимыми от частоты и объединить в один угол j _кs . Тогда уравнение баланса фаз упростится и примет вид:

j _э(w) + j _кs = 0 Для анализа влияния различных факторов на стабильность частоты это уравнение удобно представить графически (рис.2.9). Частота автоколебаний определяется абсциссой точки пересечения фазовой характеристики контура j_э(w) c прямой линией j _кs.

Влияние добротности контура.

При уменьшении добротности контура его фазовая характеристика становится более пологой, поэтому при изменении углов j_кs изменение частоты автоколебаний тем больше, чем меньше добротность контура Q (рис.2.9а). Можно показать, что фиксирующая способность контура s =w₀@ 2Q.

Влияние эталонности контура.

Под эталонностью контура понимается его способность сохранять постоянной собственную частоту при изменении тех или иных внешних условий. Влияние недостаточной эталонности контура при неизменной величине углов j_кs иллюстрирует рис.2.9б.

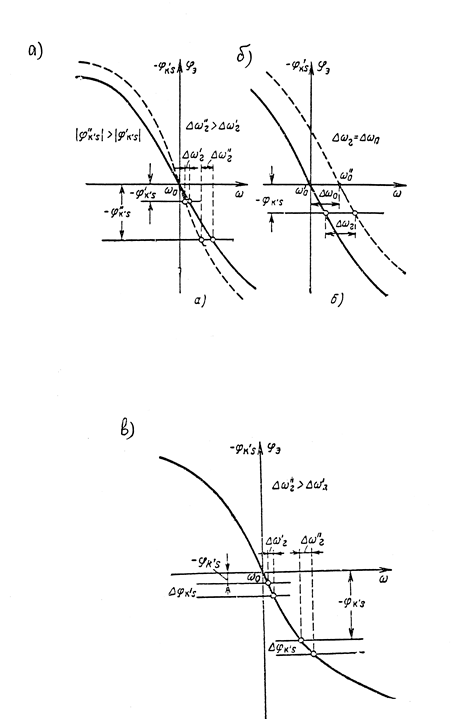
Рис. 2.9

Эталонность контура зависит не только от качества его деталей (конденсаторов и катушек индуктивности), но и от степени постоянства тех междуэлектродных и монтажных емкостей, которые добавляются к контуру, эти емкости обозначают DС_а0. Эталонность контура характеризуют формулой:

, (2.11)

где w₀ - рабочая частота автогенератора, R_э - эквивалентное сопротивление нагрузки лампы, Q - добротность контура. Из этой формулы следует, что эталонность контура тем выше, чем выше его добротность и чем ниже частота автоколебаний, поэтому для повышения стабильности частоты целесообразно понизить рабочую частоту автогенератора и затем использовать умножение частоты. Чем выше добротность контура, тем при меньшей его связи с лампой обеспечивается необходимая величина сопротивления R_э и поэтому в меньшей степени влияют на собственную частоту контура все подключаемые к нему малостабильные емкости DС_а0 .

Влияние абсолютной величины углов j _кs .

Поскольку фазовая характеристика контура линейна только при частотах, близких к его собственной резонансной частоте, то, как видно из рис.2.9в, следует стремиться к тому, чтобы углы j_кs были как можно меньше, а частота автоколебаний - как можно ближе к собственной частоте колебательного контура.

2.5.2. Дестабилизирующие факторы и методы борьбы с ними

В первом приближении основные дестабилизирующие факторы могут быть разделены на два класса - внешние и внутренние.

К первому классу относятся изменения температуры и влажности воздуха, атмосферного давления и т.п. Всё это влияет не собственную частоту контура и на его добротность, то есть на фазовую характеристику контура j_э(w). Для предотвращения этого влияния используют высокостабильные элементы контур (вакуумные конденсаторы, конденсаторы, в которых использованы два диэлектрика с противоположными знаками ТКЕ, катушки индуктивности, выполненные вжиганием в радио- или ультрафарфор и т.д. и т.п.), термостатирование, герметизацию, амортизацию и т.п.

Ко второму классу относятся нестабильность источников питания генераторной лампы и непостоянство её нагрузки. И то, и другое приводят к изменению электронного режима лампы и поэтому влияет на величину фазовых углов j_кs.

Для уменьшения изменения напряжений источников питания применяют стабилизированные источники питания, а также питание анодной цепи задающего генератора от автономного источника. Кроме того, в автогенераторе используется режим работы без сеточных токов. Помогает также использование в автогенераторе автоматического смещения, которое стабилизирует режим.

Для уменьшения влияния изменений сопротивления нагрузки уменьшают связь контура с нагрузкой, а также применяют специальные схемы , мало чувствительные к изменениям сопротивления нагрузки - сложные трёхточечные схемы, схему Шембеля и др. Кроме того, после автогенератора следует использовать каскад, работающий в буферном режиме.

2.5.3. Схема Шембеля

Нагрузкой контура задающего генератора в передатчике может быть либо антенна, либо цепь управляющей сетки следующей ступени. В обоих случаях параметры нагрузки нестабильны и реакция нагрузки на контур задающего генератора изменяется, в результате частота автоколебаний нестабильна. 0дин из способов устранения влияния нагрузки на стабильность частоты автоколебаний состоит в том, что после задающего генератора ставится буферный каскад, работающий без тока управляющей сетки. Однако, в буферном режиме генераторные лампы отдают небольшую полезную мощность, из-за этого увеличивается число каскадов усиления, что нежелательно. Схему автогенератора на одной лампе, которая обеспечивает удовлетворительную стабильность частоты при работе на нагрузку с нестабильными параметрами, была предложена Б. К. Шембелем в 1933 г. (и одновременно в США - Д.Б.Доу). Схема Шембеля (рис.2.10) содержит лампу и два колебательных контура, I и II, включенных последовательно в ее анодную цепь. Контур II, связанный с нагрузкой, называют внешним, контур I - внутренним, он обеспечивает самовозбуждение автогенератора. Оба контура питаются анодным током лампы. Амплитуда напряжения на аноде распределяется между контурами в соответствии с величинами их резонансных сопротивлений. Пропорционально амплитудам напряжений на контурах распределяется и мощность, развиваемая лампой в анодной цепи. Мощность во внутреннем контуре теряется бесполезно, а выделение тепла во внутреннем контуре является вредным, поскольку это приводит к постепенному изменению параметров контура и, следовательно, к изменению частоты автоколебаний. В связи с этим из энергетических соображений, а также из соображений

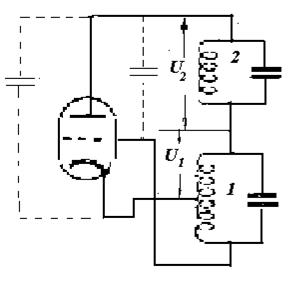
Рис.2.10

стабильности частоты, желательно, чтобы мощность, выделяемая во внутреннем контуре, была мала по сравнению с мощностью, выделяемой во внешнем контуре. С этой целью резонансные сопротивления контуров выбирают так, чтобы значительная доля анодного напряжения приходилась на внешний контур и только небольшая его часть - на внутренний (обычно R_э2 = (6-7)R_э1). Благоприятным является также и то обстоятельство, что при малом резонансном сопротивлении внутреннего контура нестабильность межэлектродных ёмкостей лампы будет меньше сказываться на частоте автоколебаний. Однако, частота автоколебаний генератора, построенного по схеме рис.2.10, зависит не только от параметров внутреннего контура, но и от параметров внешнего контура. Во-первых, внешний контур связан с внутренним ёмкостями анод-сетка и анод-катод лампы (они показаны пунктиром на рис.2.10.), а также паразитными ёмкостями монтажа между проводниками, подходящими к аноду и сетке, на корпус вне лампы (рис.2.11.) Во-вторых, между контурами существует и гальваническая связь через внутреннее сопротивление лампы (рис.2.11). Согласно эквивалентной схеме рис.2.12 анодный ток равен:

,

где R_э= R_эI + R_эII . При >> (R_эI + R_эII) влияние изменения эквивалентного сопротивления внешнего контура невелико, поскольку анодный ток зависит только от внутреннего сопротивления лампы и напряжения U_gm, которое определяется обратной связью - связью сеточной цепи с внутренним контуром.

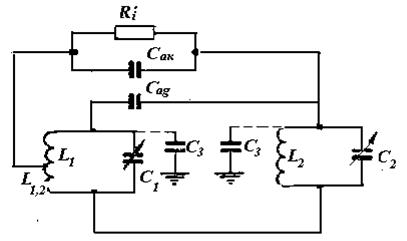
Рис.2.11

Изменение частоты автоколебаний возможно также при изменении переменного напряжения на аноде, так как при этом меняется управляющее напряжение U_упр= U_g - DU_к,, это приводит к изменению электронного режима лампы, что в свою очередь вызывает уход частоты генератора. Реакция анодного напряжения особенно сильна при работе лампы в перенапряжённом режиме. Для ослабления влияния изменения напряжения на аноде на работу схемы необходимо, чтобы лампа обладала малой проницаемостью и большим внутренним сопротивлением. Для устранения паразитной ёмкостной связи между контурами необходимо их разделить электростатическим экраном. Роль электростатического экрана внутри лампы может выполнить достаточно густая экранная сетка, расположенная между анодом и управляющей сеткой. Обычно в схеме Шембеля используют тетроды и пентоды, внутреннее сопротивление которых очень велико.

Реакция анодного напряжения на ток управляющей сетки у тетродов выражена слабо. Слабо она сказывается и на токе эмиссии, поскольку у тетродов мала результирующая проницаемость D = D₁D₂, однако в перенапряжённом режиме реакция всё же имеет место.

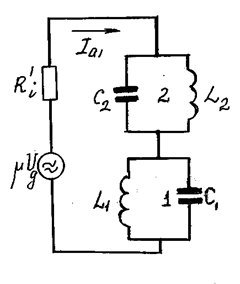
Рис.2.12

Таким образом, изменение режима внутренней части схемы, а следовательно и частоты автоколебаний, от изменения параметров внешнего контура через реакцию анодного напряжения возможно лишь в небольшой степени. В схеме Шембеля на пентоде защитная сетка, так же как и экранная, должна по высокой частоте соединяться с экраном.

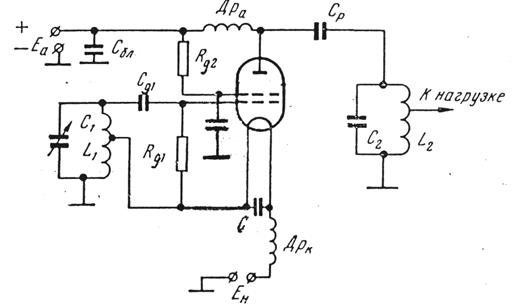
Рис. 2.13

На рис.2.13 представлена схема Шембеля на тетроде. Внутренний контур построен по схеме индуктивной трёхточки. Ток накала подводится через часть витков катушки L₁ внутреннего контура и блокировочный дроссель. Экранная сетка соединена с землей по высокой частоте ёмкостью. Напряжение на экранную сетку подаётся от источника анодного питания через потенциометр.

Особенность режима генератора, построенного по схеме Шембеля, заключается в наличии переменного напряжения между экранирующей сеткой и катодом, находящегося в фазе с переменным напряжением на аноде, и в протекании через внутренний контур I не только первой гармоники анодного тока I_a1, но и первой гармоники тока экранной сетки I_g21. При настроенных контурах переменные напряжения на электродах тетрода относительно катода определяются следующими формулами.

Переменное напряжение между анодом и катодом равно:

U_aк= I_a1(R_эI + R_эII) + I_g21R_эI

Переменное напряжение на внутреннем контуре:

U_I= (I_a1+ I_g21)R_эI

Переменное напряжение на анодном контуре:

U_II= I_a1R_эII

Мощность в нагрузочном (внешнем) контуре (полезная мощность) равна:

Р_~н= 0,5 R_эII

Мощность во внутреннем контуре - бесполезна, она равна:

Р_~I= 0,5 (I_a1+ I_g21)² R_эI

Колебательная мощность, развиваемая лампой :

Р_~л= 0,5(R_эI + R_эII) = 0,5R_эII(1+)

Эта мощность распределяется между контурами пропорционально их эквивалентным сопротивлениям.

Потери на аноде и на экранной сетке вычисляют по формулам:

Р_а= Е_а I_a0 - Р_~л = Е_а I_a0 - 0,5(R_эI + R_эII).

и

P_g2= Е_g2 I_g20 - 0,5R_эI

Схема Шембеля может успешно работать и в режиме умножения частоты. В этом случае второй контур настраивается на вторую или третью гармонику анодного тока.

2.6. Особенности автогенераторов на транзисторах

Сходство характеристик транзисторов и ламп позволяет для автогенераторов на транзисторах использовать классификацию режимов, принципы построения и методы расчета, разработанные в теории ламповых автогенераторов. Однако, автогенераторы на транзисторах обладают рядом специфических особенностей, обусловленных свойствами транзисторов. Одна из них вызвана тем, что характеристики коллекторного тока транзистора - правые. Поэтому в автогенераторах необходимо подавать на базу начальное напряжение смещения, при котором величина крутизны характеристики коллекторного тока в точке покоя достаточна для самовозбуждения. Вторая особенность связана с тем, что крутизна характеристик транзисторов намного больше, чем у ламп, поэтому при одинаковой величине обратной связи К для выполнения условия самовозбуждения (2.3) требуются низкие значения эквивалентного сопротивления нагрузки, а при этом не удаётся реализовать достаточно высокие значения характеристического сопротивления r и добротности Q колебательного контура. Для их увеличения используют схему Клаппа, представляющую собой модификацию простой ёмкостной трёхточки, у которой в индуктивную ветвь контура включен конденсатор С₃ (рис.2.14).

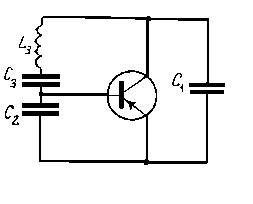
Рис.2.14

Соответствующим выбором величины ёмкости С₃ можно уменьшить коэффициент включения р= , где r=X_L , и, тем самым, увеличить r и L так, чтобы значительно повысить добротность контура Q. Благодаря повышению добротности контура стабильность частоты автогенераторов, построенных по схеме Клаппа, больше, чем при использовании простой ёмкостной трехточки, которая обеспечивает наилучшую стабильность частоты, поскольку в этой схеме слабее всего сказывается изменение состава высших гармоник коллекторного тока (напряжение обратной связи здесь снимается с ёмкости - рис.2.6б).

Нестабильность частоты транзисторных автогенераторов определяется тем, что под воздействием дестабилизирующих факторов (изменения питающих напряжений, температуры и др.) изменяются как параметры контура, так и самого транзистора. Влияние дестабилизирующих факторов на параметры контуров транзисторных автогенераторов проявляется так же, как и в ламповых.

2.7. Кварцевая стабилизация частоты

Стабильность частоты автогенератора, как мы видели, определяется главным образом качеством его колебательной системы - её эталонными свойствами и добротностью. У обычного электрического колебательного контура эталонные свойства и добротность недостаточны для обеспечения необходимых норм по стабильности частоты. Стабильность частоты автогенераторов с электрическими колебательными контурами как правило не лучше 10 ^{- 4} . В тех случаях, когда требуется более высокая стабильность, используют кварцевую колебательную систему. Использование механических колебаний кварца для получения электрических колебаний возможно благодаря прямому и обратному пьезоэлектрическим эффектам. Прямой пьезоэффект состоит в том, что механические деформации сжатия и растяжения пластинки кварца сопровождается появлением электрических зарядов на её гранях. Благодаря обратному пьезоэффекту у пластинки кварца, помещенной в электрическое поле, возникают деформации сжатия и растяжения и на её гранях появляются заряды за счет прямого пьезоэффекта. Будучи механической колебательной системой с распределёнными параметрами пластинка кварца подобно, например, электрической длинной линии обладает множеством собственных частот.

2.7.1. Электрическая эквивалентная схема кварца

Благодаря явлению пьезоэлектричества пластинку кварца в электрической схеме можно заменить некоторым колебательным контуром с сосредоточенными параметрами. Упрощенная эквивалентная электрическая схема кварцевой пластины (резонатора) изображена на рис. 2.15а, где С ₀ - её статическая ёмкость (диэлектрическая проницаемость кварца e =4,6), к которой в реальных схемах ещё добавляется паразитная ёмкость кварцедержателя; С_q , L_q и r_q - пьезоэлектрические эквивалентные параметры. Порядок их величин (при используемых на коротких волнах механических колебаниях пластины по толщине): С₀ - единицы пФ, С_q -сотые доли пФ, L_q - десятые доли Гн , r_q- от единиц до ста Ом. Добротность кварцевых резонаторов достигает сотен тысяч. Эталонность кварца весьма высока. Кроме того, благодаря малым размерам кварцевой пластины её легко термостатировать и т.п. Изображенная на рис.2.15а колебательная система имеет два резонанса - последовательный при w= w_q (собственный резонанс кварца) и параллельный при w=w₀ (колебательного контура в целом).

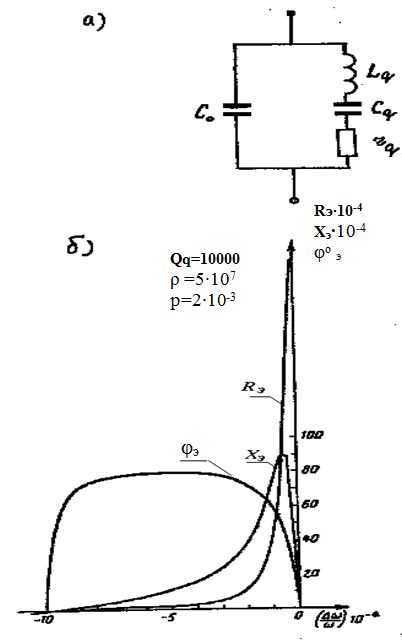
Рис.2.15

Разность между частотами последовательного и параллельного резонансов с уменьшением добротности уменьшается. При Q= 2/p , где p= C_q/C₀ , эти частоты совпадают. При большой добротности отношение (w₀-w_q)/w_q @p/2 @2×10^-3 На рис. 2.15б, изображены кривые зависимостей реактивного X_q и активного R_q сопротивлений, а также фазового угла j_э эквивалентной схемы кварца от относительной расстройки частоты Dw/w. Из графиков видно, что в интервале между частотами последовательного и параллельного резонансов производная ¶j_э/¶w < 0, как у параллельного колебательного контура, а эквивалентное сопротивление кварца X_q здесь имеет индуктивный характер.

2.7.2. Схемы кварцевых генераторов

Различают два класса схем кварцевых генераторов. К первому классу относятся так называемые осцилляторные схемы, в которых генератор работает приблизительно на частоте параллельного резонанса кварцевого контура, так как только здесь получается необходимый для самовозбуждения сдвиг фаз и обеспечивается устойчивость автоколебаний. В осцилляторных схемах кварц включают в те участки обобщенной трехточечечной схемы генератора, где для поддержания автоколебаний эквивалентное сопротивление кварца должно иметь индуктивный характер (рис2.16).

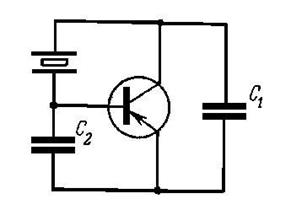
Рис.2.16

Наличие колебаний в осцилляторной схеме всегда служит гарантией того, что она действует благодаря пьезоэффекту кварца. Следует отметить, что частота автоколебаний в этих схемах очень мало отличается от частоты параллельного резонанса кварцевого контура, поскольку ширина кривой полного сопротивления этого контура, которая пропорциональна затуханию кварца d_q=1/Q_q , значительно меньше ширины расстройки между частотами w_q и w₀ , поскольку d_q может рассматриваться как величина второго порядка малости относительно величины р=С_q/C₀.

В схемах, относящихся ко второму классу, кварц возбуждается на чacтоте последовательного резонанса, эти схемы обладают большей стабильностью. Примеры этих схем показаны на рис. 2.17.

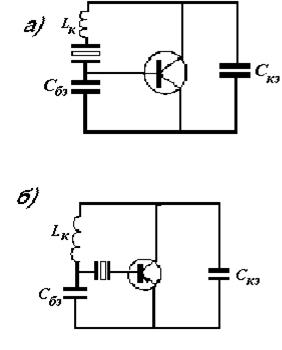
Рис.2.17

2.7.3. Кварцевая стабилизация частоты в диапазоне волн

Одним из существенных недостатков кварцевого генератора является его неспособность работать в плавном диапазоне волн, поскольку изменить плавно собственную частоту кварцевой пластины невозможно. Для стабилизации частоты в плавном диапазоне волн используется интерполяционный метод, структурная схема которого изображена на рис.2.18. Сущность его сводится к следующему.

Колебания кварцевого генератора, частота которого f_кв, и колебания с частотой f_г диапазонного бескварцевого генератора, называемого интерполяционным , подаются на смеситель. После смесителя установлен селектор, который выделяет колебания требуемой рабочей частоты f = f_кв + f_г, или f= f_кв - f_г. Нетрудно показать, что нестабильность рабочей частоты, которая складывается из нестабильности кварцевого генератора и нестабильности интерполяционного генератора, тем ближе к нестабильности кварцевого генератора чем частота кварцевого генератора больше частоты интерполяционного генератора. Отношение N=f_кв/f_г носит название интерполяционного числа. Величина N обычно не превышает 20 из-за трудностей построения схемы селектора.

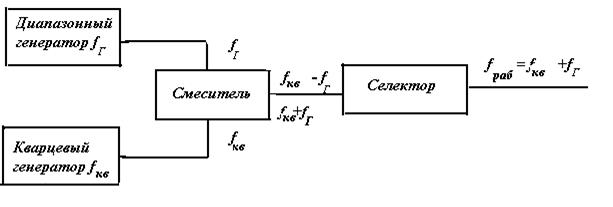
Рис.2.18