7.4.1. Пространственные характеристики сверточных кодов

7.4.1.1. Возможности сверточного кода в коррекцииошибок

7.4.2. Систематические и несистематические сверточные коды

7.4.3. Накопление катастрофических ошибок в сверточных кодах

7.4.4. Границы рабочих характеристик сверточных кодов

7.4.5. Эффективность кодирования

7.4.6. Наиболее известные сверточные коды

7.4.7. Компромиссы сверточного кодирования

7.4.7.1. Производительность при когерентнойпередаче сигналов с модуляцией PSK

7.4.7.2.Производительность при некогерентной ортогональной передаче сигналов

7.4.8. Мягкое декодирование по алгоритму Витерби

7.4.1. Пространственные характеристики сверточных кодов

Рассмотрим пространственные характеристики сверточных кодов в контексте простого кодера и его решетчатой диаграммы (рис 7.7.). Мы хотим узнать расстояние между всеми возможными парами последовательности кодовых слов. Как и в случае блочных кодов (см. раздел 6.5.2), нас интересует, минимальное расстояние между всеми такими парами последовательности таких кодовых слов в коде, поскольку минимальное расстояние связано с возможностями кода в коррекции ошибок. Поскольку сверточный код является групповым или линейным [6], можно без потери общности просто найти минимальное расстояние между последовательностью кодовых слов и нулевой последовательностью. Другими словами, для линейного кода данное контрольное сообщение окажется точно таким же «хорошим», как и любое другое. Так почему бы не взять то сообщение, которое легко проследить, а именно нулевую последовательность? Допустим, что на вход передана нулевая последовательность; следовательно, нас интересует такой путь, который начинается и заканчивается в состоянии 00 и не возвращается к состоянию 00 нигде внутри пути. Всякий раз, когда расстояние любых других путей, которые сливаются с состоянием а = 00 в момент окажется меньше расстояния нулевого пути. Иными словами, при нулевой передаче ошибка возникает всегда, когда не выживает нулевой путь. Следовательно, ошибка, о которой идет речь, связана с выживающим путем, который расходиться, а затем снова сливается с нулевым путем. Может возникнуть вопрос, зачем нужно чтобы пути сливались? Не будет ли для обнаружения ошибки достаточно лишь того, что бы пути расходились? В принципе, достаточно, но если ошибка характеризуется только расхождением, то декодер, начиная с этой точки, будет выдавать вместо оставшегося сообщения сплошной «мусор». Мы хотим выразить возможности декодера через число обычно появляющихся ошибок, то есть хотим узнать «самый легкий» для декодера способ сделать ошибку. Минимально расстояние для такой ошибки можно найти, полностью изучив все пути из состояния 00 в состояние 00. Итак, давайте заново начертим решетчатую диаграмму, как показано на рисунке 7.16, и обозначим каждую ветвь не символом ответвляющегося слова, а её расстояние Хемминга от нулевого кодового слова. Расстояние Хемминга между двумя последовательностями разной длины можно получить путем их сравнивания, т.е. прибавив к началу более короткой последовательности нужное количество нулей. Рассмотрим все пути, которые расходятся из нулевого пути и затем в какой то момент снова сливаются в произвольном узле. ИЗ диаграммы на рисунке 7.16 можно получить расстояние этих путей до нулевого пути. И так, на расстоянии 5 от нулевого пути имеется один путь; этот путь отходит от нулевого в момент в . Точно так же имеется два пути с расстоянием 6, один отходит в момент и сливается с ним в момент , а другой отходит в момент и сливается с ним в момент и т.д. Также можно видеть (по пунктирным и сплошным линиям на диаграмме), что входными битами для расстояния 5 будет 100; от нулевой последовательности эта последовательность отличается только одним битом. Точно так же входные биты для путей с расстоянием 6 будут 1100 и 10100; каждая из этих последовательностей отличается от нулевого пути в двух местах. Минимальная длина пути из числа расходящихся, а затем сливающихся путей называетсяминимальным просветом (minimum free distance), или просто просветом (free distance). Его можно видеть на рис. 7.16, где он показан жирной линией. Для оценки возможностей кода коррекции ошибок, мы повторно приведем уравнение (6.44) с заменой минимального расстояния на просвет .

(7.11)

Здесь [x] означает наибольшее целое, не большее х. Положив =5, можно видеть, что код, описываемый кодером на рис. 7.3, может исправить две любые ошибки канала.

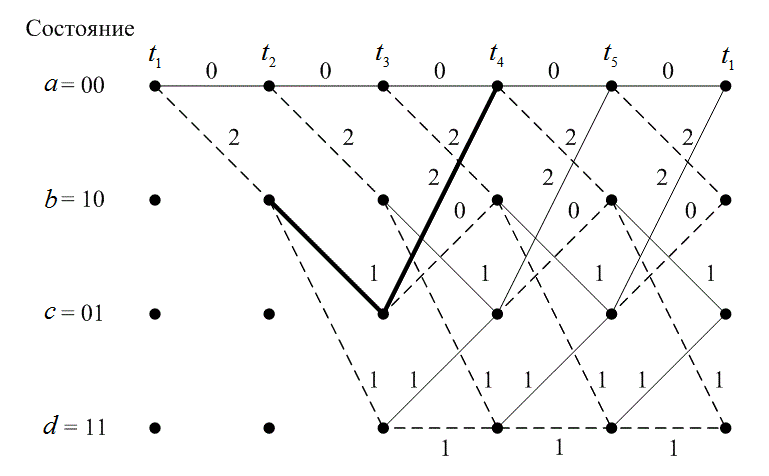
Рис. 7.16. Решетчатая диаграмма с обозначенными расстояниями от нулевого пути

Решетчатая диаграмма представляет собой "правила игры". Она является как бы символическим описанием всех возможных переходов и соответствующих начальных и конечных состояний, ассоциируемых с конкретным конечным автоматом. Эта диаграмма позволяет взглянуть глубже на выгоды (эффективность кодирования), которые дает применение кодирования с коррекцией ошибок. Взглянем на рис. 7.16 и на возможные ошибочные расхождения и слияния путей. Из рисунка видно, что декодер не может сделать ошибку произвольным образом. Ошибочный путь должен следовать одному из возможных переходов. Решетка позволяет нам определить все такие доступные пути. Получив по этому пути кодированные данные, мы можем наложить ограничения на переданный сигнал. Если декодер знает об этих ограничениях, то это позволяет ему более просто (используя меньшее ) удовлетворять требованиям надежной безошибочной работы.

Хотя на рис. 7.16 представлен способ прямого вычисления просвета, для него можно получить более строгое аналитическое выражение, воспользовавшись для этого диаграммой состояний, изображенной на рис. 7.5. Для начала обозначим ветви диаграммы состояний как , как это показано на рис. 7.17, где показатель D означает расстояние Хэмминга между ответвленным словом этой ветви и нулевой ветвью. Петлю в узле а можно убрать, поскольку она не дает никакого вклада в пространственные характеристики последовательности кодовых слов относительно нулевой последовательности. Более того, узел а можно разбить на два узла (обозначим их а и е), один из них представляет вход, а другой — выход диаграммы состояний. Все пути, начинающиеся из состояния а=00 и заканчивающиеся в е=00, можно проследить на модифицированной диаграмме состояний, показанной на рис. 7.17. Передаточную функцию пути a b c e (который начинается и заканчивается в состоянии 00) можно рассчитать через неопределенный “заполнитель” D как . Степень D — общее число единиц на пути, а значит, расстояние Хэмминга до нулевого пути. Точно так же пути a b d c e и а b c b с е имеют передаточную функцию D⁶ и, соответственно, расстояние Хэмминга, равное 6, до нулевого пути. Теперь уравнения состояния можем записать следующим образом

(7.12)

Здесь являются фиктивными переменными неполных путей между промежуточными узлами. Передаточную функцию,T(D), которую иногда называют производящей функцией кода, можно записать как . Решение уравнений состояния (7.12) имеет следующий вид [15, 16].

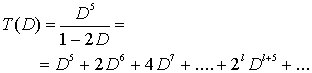(7.13)

Передаточная функция этого кода показывает, что имеется один путь с расстоянием 5 до нулевого вектора, два пути — с расстоянием 6, четыре — с расстоянием 7. Вообще, существуют пути с расстоянием l+5 до нулевого вектора, причем l = 0,1,2,... . Просвет df кода является весовым коэффициентом Хэмминга члена наименьшего порядка разложения T(D). В данном случае df=5. Для оценки пространственных характеристик при большой длине кодового ограничения передаточную функцию T(D) использовать нельзя, поскольку сложность T(D) растет с увеличением длины кодового ограничения как степенная функция.

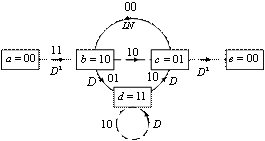
Рис. 7.17. Диаграмма состояний с обозначенными расстояниями до нулевого пути

С помощью передаточной функции можно получить более подробную информацию, чем при использовании лишь расстояния между различными путями. В каждую ветвь диаграммы состояний введем множитель L так, чтобы показатель L мог служить счетчиком ветвей в любом пути из состояния а = 00 в состояние е = 00. Более того, мы можем ввести множитель N во все ветви переходов, порожденных входной двоичной единицей. Таким образом, после прохождения ветви суммарный множитель N возрастает на единицу, только если этот переход ветви вызван входной битовой единицей. Для сверточного кода, описанного на рис. 7.3, на перестроенной диаграмме состояний (рис. 7.18) показаны дополнительные множители L и N. Уравнения (7.12) теперь можно переписать следующим образом.

(7.14)

Передаточная функция такой доработанной диаграммы состояний будет следующей.

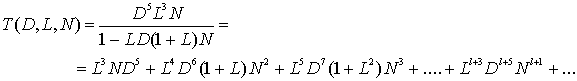(7.15)

Таким образом, мы можем проверить некоторые свойства путей, показанные на рис. 7.16. Существует один путь с расстоянием 5 и длиной 3, который отличается от нулевого пути одним входным битом. Имеется два пути с расстоянием 6, один из них имеет длину 4, другой — длину 5, и оба отличаются от нулевого пути двумя входными битами. Также есть пути с расстоянием 7, из которых один имеет длину 5, два — длину 6 и один — длину 7; все четыре пути соответствуют входной последовательности, которая отличается от нулевого пути тремя входными битами. Следовательно, если нулевой путь является правильным и шум приводит к тому, что мы выбираем один из неправильных путей, то в итоге получится три битовые ошибки.

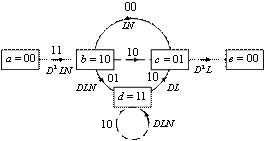
Рис. 7.18. Диаграмма состояний с обозначением расстояния, длины и числа входных единиц

7.4.1.1. Возможности сверточного кода в коррекции ошибок

В главе 6 при изучении блочных кодов говорилось, что способность кода к коррекции ошибок, t, представляет собой количество ошибочных кодовых символов, которые можно исправить в каждом блоке кода путем декодирования по методу максимального правдоподобия. В то же время при декодировании сверточных кодов способность кода к коррекции ошибок нельзя сформулировать так лаконично. Из уравнения (7.11) можно сказать, что при декодировании по принципу максимального правдоподобия код способен исправить t ошибок в пределах нескольких длин кодового ограничения, причем "несколько" — это где-то от 3 до 5. Точное значение длины зависит от распределения ошибок. Для конкретного кода и ошибочной комбинации длину можно ограничить с использованием методов передаточной функции. Такое ограничение будет описано позднее.

7.4.2. Систематические и несистематические сверточные коды

Систематический сверточный код — это код, в котором входной k-кортеж фигурирует как часть выходного n-кортежа ответвляющегося слова, соответствующего этому k-кортежу. На рис. 7.19 показан двоичный систематический кодер со степенью кодирования 1/2 и К=3. Для линейных блочных кодов любой несистематический код можно преобразовать в систематический с такими же пространственными характеристиками блоков. При использовании сверточных кодов это не так. Это означает, что сверточные коды сильно зависят от просвета; при построении сверточного кода в систематической форме при данной длине кодового ограничения и степени кодирования максимально возможное значение просвета снижается.

Рис. 7.19. Систематический сверточный кодер (степень кодирования 1/2, К=3)

В табл. 7.1 показан максимальный просвет при степени кодирования 1/2 для систематического и несистематического кодов с К от 2 до 8. При большой длине кодового ограничения результаты отличаются еще сильнее [17].

Таблица 7.1. Сравнение систематического и несистематического просветов, степень кодирования 1/2

Длина кодового ограничения	Просвет систематического кода	Просвет несистематического кода
2 3 4 5 6 7 8	3 4 4 5 6 6 7	3 5 6 7 8 10 10

Источник:. A. J. Viteibi and J. К. Omura. Principles of Digital Communication and Coding, McGraw-Hill Book Company, New-York, 1979, p. 251.

7.4.3. Накопление катастрофических ошибок в сверточных кодах

Катастрофическая ошибка возникает, когда конечное число ошибок в кодовых символах вызывает бесконечное число битовых ошибок в декодированных данных. Мэсси (Massey) и Сейн (Sain) указали необходимые и достаточные условия для сверточного кода, при которых возможно накопление катастрофических ошибок. Условием накопления катастрофических ошибок для кода со степенью кодирования 1/2, реализованного на полиномиальных генераторах, описанных в разделе 7.2.1, будет наличие у генераторов общего полиномиального делителя (степени не менее единицы). Например, на рис. 7.20, а показан кодер с К = 3, степенью кодирования 1/2, со старшим полиномом и младшим .

(7.16)

Генераторы и имеют общий полиномиальный делитель 1+X, поскольку

.

Следовательно, в кодере, показанном на рис. 7.20, а, может происходить накопление катастрофической ошибки.

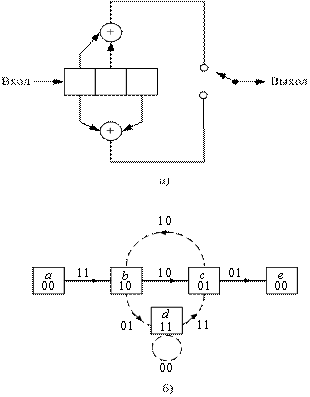
Рис. 7.20. Кодер, в котором возможно накопление катастрофической ошибки: а) кодер; б) диаграмма состояний

Если говорить о диаграмме состояний кода произвольной степени кодирования, то катастрофическая ошибка может появиться тогда и только тогда, когда любая петля пути на диаграмме имеет нулевой весовой коэффициент (нулевое расстояние до нулевого пути). Чтобы проиллюстрировать это, рассмотрим пример, приведенный на рис. 7.20. На диаграмме (рис. 7.20, б) узел состояния а = 00 разбит на два узла, а и е, как и ранее. Допустим, что нулевой путь является правильным, тогда неправильный путь a b d d... d c e имеет точно 6 единиц, независимо от того, сколько раз мы обойдем вокруг петли в узле d. Поэтому, например, для канала BSC к выбору этого неправильного пути могут привести три канальные ошибки. На таком пути может появиться сколь угодно большое число ошибок (две, плюс количество раз обхода петли). Для кодов со степенью кодирования 1/n можно видеть, что если каждый сумматор в кодере имеет четное количество соединений, петли, которые соответствуют информационным состояниям со всеми единицами, будут иметь нулевой вес, и, следовательно, код будет катастрофическим.

Единственное преимущество описанного ранее систематического кода заключается в том, что он никогда не будет катастрофическим, поскольку каждая петля должна содержать по крайней мере одну ветвь, порождаемую ненулевым входным битом; следовательно, каждая петля должна содержать ненулевой кодовый символ. Впрочем, можно показать [19], что только небольшая часть несистематических кодов (исключая тот, в котором все сумматоры имеют четное количество соединений) является катастрофической.

7.4.4. Границы рабочих характеристик сверточных кодов

Можно показать [8], что вероятность битовой ошибки в бинарном сверточном коде, использующем при декодировании жесткую схему принятия решений, может быть ограничена сверху следующим образом.

(7.17)

где p — вероятность ошибки в канальном символе. Для примера, приведенного на рис. 7.3, T(D,N) получено из T(D, L, N) путем задания L=1 в уравнении (7.15).

(7.18)

и

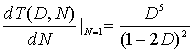(7.19)

Объединяя уравнения (7.17) и (7.19), можем записать следующее.

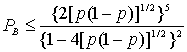(7.20)

Можно показать, что при когерентной модуляции BPSK в канале с аддитивным белым гауссовым шумом (additive white Gaussian noise — AWGN) вероятность битовой ошибки ограничивается следующей величиной.

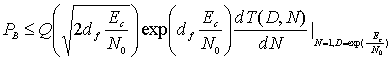(7.21)

где

— отношение энергии информационного бита к спектральной плотности мощности шума,

— отношение энергии канального символа к спектральной плотности мощности шума,

—степень кодирования,

а Q(x) определяется уравнениями (3.43) и (3.44) и приведено в табл. Б.1. Следовательно, для кода со степенью кодирования 1/2 и просветом df=5, при использовании когерентной схемы BPSK и жесткой схемы принятия решений при декодировании, можем записать следующее.

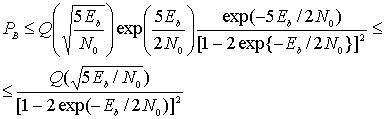(7.22)

7.4.5. Эффективность кодирования

Эффективность кодирования, представленная уравнением (6.19), определяется как уменьшение (обычно выраженное в децибелах) отношения , требуемого для достижения определенной вероятности появления ошибок в кодированной системе, по сравнению с не кодированной системой с той же модуляцией и характеристиками канала. В табл. 7.2 перечислены верхние границы эффективности кодирования. Они сравниваются с не кодированным сигналом с когерентной модуляцией BPSK для нескольких значений минимальных просветов сверточного кода. Длина кодового ограничения в гауссовом канале с жесткой схемой принятия решений при декодировании изменяется от 3 до 9. В таблице отражен тот факт, что даже при использовании простого сверточного кода можно достичь значительной эффективности кодирования. Реальная эффективность кодирования будет изменяться в зависимости от требуемой вероятности появления битовых ошибок [20].

Таблица 7.2. Верхние границы эффективности кодирования для некоторых сверточных кодов

Коды со степенью кодирования 1/2			Коды со степенью кодирования 1/2
K		Верхняя граница (дБ)	К		Верхняя граница (дБ)
3 4 5 6 7 8 9	5 6 7 8 10 10 12	3,97 4,76 5,43 6,00 6,99 6,99 7,78	3 4 5 6 7 8 9	8 10 12 13 15 16 18	4,26 5,23 6,02 6,37 6,99 7,27 7,78

Источник: V. К. Bhargava, D. Haccoun, R. Matyas and P. Nuspl. Digital Communications by Satellite. John Wiley & Sons, Inc., New York, 1981.

В табл. 7.3 приводятся оценки эффективности кодов, сравниваемые с не кодированным сигналом с когерентной модуляцией BPSK, реализованной аппаратным путем или путем моделирования на компьютере, в гауссовом канале с мягкой схемой принятия решений при декодировании [21]. Не кодированное значение дано в крайнем левом столбце. Из табл. 7.3 можно видеть, что эффективность кодирования возрастает при уменьшении вероятности появления битовой ошибки. Однако эффективность кодирования не может возрастать бесконечно. Как показано в таблице, она имеет верхнюю границу. Эту границу (в децибелах) можно выразить следующим образом.

эффективность кодирования (7.23)

Здесь r— степень кодирования, a df— просвет. При изучении табл. 7.3 обнаруживается также, что (при ) для кодов со степенью кодирования 1/2 и 2/3 более слабые коды имеют тенденцию находиться ближе к верхней границе, чем более мощные коды.

Таблица 7.3. Основные значения эффективности кодирования (в дБ) при использовании мягкой схемы принятия решений в ходе декодирования по алгоритму Витерби

Не кодированное	Степень кодирования		1/3			½			2/3		3/4
(дБ)		К	7	8	5	6	7	6	8	6	9
6,8 9,6 11,3 Верхняя граница			4,2 5,7 6,2 7,0	4,4 5,9 6,5 7,3	3,3 4,3 4,9 5,4	3,5 4,6 5,3 6,0	3,8 5,1 5,8 7,0	2,9 4,2 4,7 5,2	3,1 4,6 5,2 6,7	2,6 3,6 3,9 4,8	2,6 4,2 4,8 5,7

Источник: I. M. Jacobs. Practical Applications of Coding. IEEE Trans. Inf. Theory, vol. IT20, May 1974, pp. 305-310. .

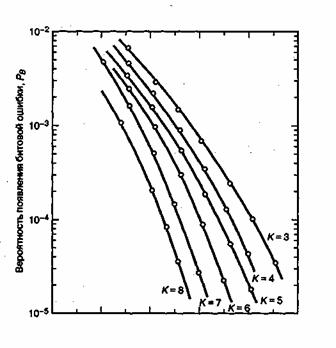
Как правило, декодирование по алгоритму Витерби используется в двоичном входном канале с жестким или мягким 3-битовым квантованным выходом. Длина кодового ограничения варьируется от 3 до 9, причем степень кодирования кода редко оказывается меньше 1/3, и память путей составляет несколько длин кодового ограничения [12]. Памятью путей называется глубина входных битов, которая сохраняется в декодере. После рассмотрения в разделе 7.3.4 декодирования по алгоритму Витерби может возникнуть вопрос об ограничении объема памяти путей. Из этого примера может показаться, что декодирование ответвленного слова в любом узле может происходить сразу, как только останется один выживший путь в этом узле. Это действительно так; хотя для создания реального декодера таким способом потребуется большое количество постоянных проверок после декодирования ответвленного слова. На практике вместо всего этого обеспечивается фиксированная задержка, после которой ответвляющееся слово декодируется. Было показано [12, 22], что информации о происхождении состояния с наименьшей метрикой состояния (с использованием фиксированного объема путей, порядка 4 или 5 длин кодового ограничения) достаточно для получения характеристик декодера, которые для гауссова канала и канала BSC на величину порядка 0,1 дБ меньше характеристик оптимального канала. На рис. 7.21 показаны характерные результаты моделирования достоверности передачи при декодировании по алгоритму Витерби с жесткой схемой квантования [12]. Заметьте, что каждое увеличение длины кодового ограничения приводит к улучшению требуемого значения на величину, равную приблизительно 0,5 дБ, при .

7.4.6. Наиболее известные сверточные коды

Векторы связи или полиномиальные генераторы сверточного кода обычно выбираются исходя из свойств просветов кода. Главным критерием при выборе кода является требование, чтоб код не допускал катастрофического накопления ошибок и имел максимальный просвет при данной степени кодирования и длине кодового ограничения.

(дБ)

Рис. 7.21. Зависимость вероятности появления битовой ошибки от при степени кодирования кодов 1/2; используется когерентная модуляция BPSK в канале ВSС, декодирование согласно алгоритму Витерби и 32-битовая (Перепечатано с разрешения авторов из J. A. Heller and I. M. Jacobs. "Viterbi Decoding for Satellite and Space Communication". IEEE Trans. Commun. Technol., vol. COM19, n. 5, October, 1971, Fig. 7, p. 84 © 1971, IEEE.)

Затем при данном просвете df минимизируется число путей или число ошибочных битов данных, которые представляют путь. Процедуру выбора можно усовершенствовать, рассматривая количество путей или ошибочных битов при df+1, df +2и т.д., пока не останется только один код или класс кодов. Список наиболее известных кодов со степенью кодирования 1/2 при K , равном от 3 до 9, и со степенью кодирования 1/3 при K, равном от 3 до 8, соответствующих этому критерию, был составлен Оденуальдером (Odenwalder) [3, 23] и приводится в табл. 7.4. Векторы связи в этой таблице представляют наличие или отсутствие (1 или 0) соединения между соответствующими регистрами сверточного кодера, причем крайний левый элемент соответствует крайнему левому разряду регистра кодера. Интересно, что эти соединения можно обратить (заменить в указанной выше схеме крайний; левые на крайние правые). При декодировании по алгоритму Витерби обратные соединения приведут к кодам с точно такими же пространственными характеристиками, а значит, и с такими же рабочими характеристиками, как показаны в табл. 7.4.

Таблица 7.4. Оптимальные коды с малой длиной кодового ограничения (степень кодирования 1/2 и 1/3)

Степень кодирования	Длина кодового ограничения	Просвет	Вектор кода
1/2	3	5	111 101
1/2	4	6	1111 1011
1/2	5	7	10111 11001
1/2	6	8	101111 110101
1/2	7	10	10011111 11100101
1/2	8	10	110101111 11100101
1/2	9	12	110101111 100011101 111
1/3	3	8	111 101 1111
1/3	4	10	1011 1101 11111
1/3	5	12	11011 10101 10111
1/3	6	13	110101 111001 1001111
1/3	7	15	1010111 1101101 11101111
1/3	8	16	10011011 10101001

Источник: J. P. Odenwalder. Error Control Coding Handbook. Linkabit Corp., San Diego, Calif., July, 15, 1976.

7.4.7. Компромиссы сверточного кодирования

7.4.7.1. Производительность при когерентной передаче сигналов с модуляцией PSK

Возможности схемы кодирования в коррекции ошибок возрастают при увеличении числа канальных символов n, приходящихся на число информационных бит k, или при снижении степени кодирования k/n. В то же время при этом увеличивается ширина полосы пропускания канала и сложность декодера: Выгода низких степеней кодирования при использовании сверточного кода совместно с когерентной модуляцией PSK проявляется в снижении требуемого значения (для широкого диапазона степеней кодирования), что позволяет при заданном значении мощности осуществить передачу на более высоких скоростях или снизить мощность при заданной скорости передачи информации. Компьютерное моделирование показало [16, 22], что при фиксированной длине кодового ограничения снижение степени кодирования с 1/2 до 1/3 в итоге приводит к уменьшению требуемого значения примерно на 0,4 дБ (сложность декодера при этом возрастает примерно на 17%). Для меньших значений степени кодирования улучшение рабочих характеристик по отношению к росту сложности декодирования быстро убывает [22]. В конечном счете, существует точка, по достижении которой дальнейшее снижение степени кодирования приводит к падению эффективности кодирования (см. раздел 9.7.7.2).

7.4.7.2. Производительность при некогерентной ортогональной передаче сигналов

В отличие от модуляции PSK, при некогерентной ортогональной передаче сигналов существует оптимальное значение степени кодирования, приблизительно равное 1/2. Надежность передачи при степени кодирования 1/3, 2/3 и 3/4 хуже, чем при степени кодирования 1/2. При фиксированной длине кодового ограничения и степени кодирования 1/3, 2/3 или 3/4 качество кодирования, как правило, падает на 0,25, 0,5 и 0,3 дБ, соответственно, по сравнению с достоверностью передачи при Степени кодирования 1/2 [16].

7.4.8. Мягкое декодирование по алгоритму Витерби

Для двоичной кодовой системы со степенью кодирования 1/2, демодулятор подает на декодер два кодовых символа за раз. Для жесткого (двухуровневого) декодирования каждую пару принятых кодовых символов можно изобразить на плоскости в виде одного из углов квадрата, как показано на рис. 7.22, а. Углы помечены двоичными числами (0, 0), (0, 1), (1, 0) и (1, 1), представляющими четыре возможных значения, которые могут принимать два кодовых символа в жесткой схеме принятия решений. Аналогично для 8-уровневого мягкого декодирования каждую пару кодовых символов можно отобразить на плоскости в виде равностороннего прямоугольника размером 8x8, состоящего из 64 точек, как показано на рис. 7.22, б. В этом случае демодулятор больше не выдает жестких решений; он выдает квантованные сигналы с шумом (мягкая схема принятия решений).

Основное различие между мягким и жестким декодированием по алгоритму Витерби состоит в том, что в мягкой схеме не используется метрика расстояния Хэмминга, поскольку она имеет ограниченное разрешение. Метрика расстояний, которая имеет нужное разрешение, называется евклидовым кодовым расстоянием, поэтому далее, чтобы облегчить ее применение, соответствующим образом преобразуем двоичные числа из единиц и нулей в восьмеричные числа от 0 до 7. Это можно увидеть на рис. 7.22, в, где соответствующим образом обозначены углы квадрата; теперь для описания любой из 64 точек мы будем пользоваться парами целых чисел от 0 до 7. На рис. 7.22, в также изображена точка 5,4, представляющая пример пары значений кодовых символов с шумом. Представим себе, что квадрат на рис. 7.22, в изображен в координатах (x, y). Каким будет евклидово кодовое расстояние между точкой с шумом 5,4 и точкой без шума 0,0? Оно равно . А если мы захотим узнать евклидово кодовое расстояние между точкой с шумом 5,4 и точкой без шума 7,7? Аналогично .

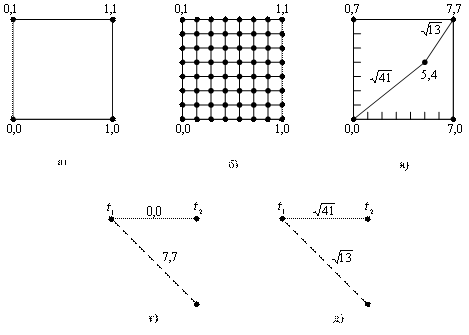
Рис. 7.22. Декодирование Витерби: а) плоскость жесткой схемы принятия решений; б) 8-уровневая плоскость мягкой схемы принятия решений; в) пример мягких кодовых символов; г) секция решетки кодирования; д) секция решетки декодирования

Мягкое декодирование по алгоритму Витерби, по большей части, осуществляется так же, как и жесткое декодирование (как описывалось в разделах 7.3.4 и 7.3.5). Единственное отличие состоит в том, что здесь не используется расстояние Хэмминга. Поэтому рассмотрим мягкое декодирование, осуществляемое с евклидовым кодовым расстоянием. На рис. 7.22, г показана первая секция решетки кодирования, которая вначале имела вид, приведенный на рис. 7.7. При этом кодовые слова преобразованы из двоичных в восьмеричные. Допустим, что пара кодовых символов, поступившая на декодер во время первого перехода, согласно мягкой схеме декодирования имеет значения 5,4. На рис. 7.22, д показана первая секция решетки декодирования. Метрика (), представляющая евклидово кодовое расстояние между прибывшим ответвленным словом 5,4 и ответвленным словом 0,0, обозначена сплошной линией. Аналогично метрика () представляет собой евклидово кодовое расстояние между поступившим кодовым символом 5,4 и кодовым символом 7,7; это расстояние показано пунктирной линией. Оставшаяся часть задачи декодирования, которая сводится к отсечению решетки и поиску полной ветви, осуществляется аналогично схеме жесткого декодирования. Заметим, что в реальных микросхемах, предназначенных для сверточного декодирования, евклидово кодовое расстояние в действительности не применяется, вместо него используется монотонная метрика, которая обладает сходными свойствами, но значительно проще в реализации. Примером такой метрики является' квадрат евклидова кодового расстояния, в котором исключается рассмотренная выше операция взятия квадратного корня. Более того, если двоичные кодовые символы представлены биполярными величинами, тогда можно использовать метрику скалярного произведения, определяемую уравнением (7.9). При такой метрике вместо минимального расстояния мы должны будем рассматривать максимальные корреляции.