Для линейного резистивного элемента R существует прямая пропорциональная зависимость между протекающим через этот элемент током i и приложенным к нему напряжение u (рис. 5.1):

или . (5.1)

Уравнение (5.1) называется вольт-амперной характеристикой (ВАХ) резистивного элемента. Так как R постоянно, то ВАХ линейна.

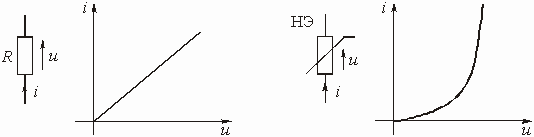
Рис. 5.1                                                      Рис. 5.2

Для нелинейного резистивного элемента характерна нелинейная связь между током i и напряжением u (рис. 5.2). Сопротивление нелинейного резистивного элемента (НЭ) не является постоянным, а зависит от того, в какой точке ВАХ оно определяется. На рис. 5.3 изображена ВАХ нелинейного элемента. Можно определить сопротивление как

,

где – приложенное к нелинейному элементу постоянное напряжение; – протекающий через нелинейный элемент постоянный ток. Это сопротивление постоянному току (или статическое). Оно зависит от приложенного напряжения.

Пусть на нелинейный элемент действует сумма постоянного напряжения и гармонического , причем амплитуда переменной составляющей достаточно мала (рис. 5.3), так что тот небольшой участок ВАХ, в пределах которого действует переменное напряжение, можно считать линейным. Проектируя каждое мгновенное значение гармонического напряжения на ВАХ и отображая результат проекции на плоскости “ток – время” , получим зависимость тока от времени. В силу того, что выбран линейный участок ВАХ ток, протекающий через нелинейный элемент, повторит по форме напряжение: (рис. 5.3). Отношение амплитуды переменного напряжения к амплитуде переменного тока (на графике это отношение приращения напряжения к приращению тока ) называют дифференциальным (динамическим) сопротивлением нелинейного элемента, которое, по сути, является сопротивлением нелинейного элемента переменному току малой амплитуды:

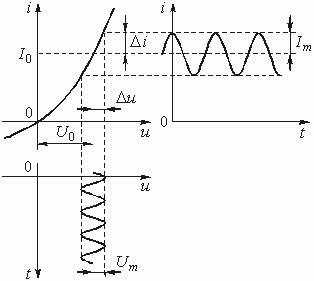
Рис. 5.3

.

Обычно переходят к пределу этих приращений и определяют дифференциальное сопротивление в виде . Часто удобно пользоваться понятием дифференциальной крутизны (проводимости):

.

Наиболее распространенными приборами с нелинейным резистивным сопротивлением являются ламповые и полупроводниковые приборы (диоды, транзисторы и т. п.), используемые в радиотехнике для преобразования и усиления сигналов. На рис. 5.4 приведены ВАХ типовых нелинейных резисторов и их условные обозначения: полупроводникового (а) и туннельного (б) диодов; биполярного (в) и полевого (г) транзисторов. Здесь , и – соответственно напряжение, приложенное к участку “база – эмиттер” , и токи базы и коллектора биполярного транзистора; и – соответственно напряжение, приложенное к участку “затвор – исток” и ток стока полевого транзистора.

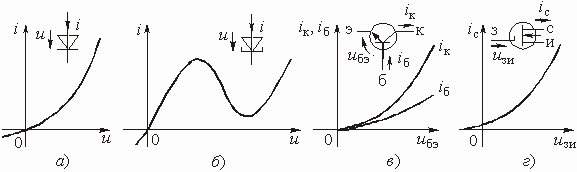
Рис. 5.4

Приборы, имеющие падающие участки ВАХ (см. рис. 5.4, б), называются приборами с отрицательным сопротивлением, т.к. .

Расчет нелинейных цепей, ВАХ нелинейных элементов (НЭ) которых заданы графически или описываются сложными функциями, проводят графоаналитическими методами. Суть этих методов состоит в составлении системы аналитических уравнений, которые затем решаются графически. Точки пересечения графиков дают искомое решение.

Для расчета цепи, содержащей один НЭ, естественно применить метод эквивалентного генератора, при этом линейная цепь относительно зажимов НЭ заменяется эквивалентным генератором напряжения или тока (рис. 5.5).

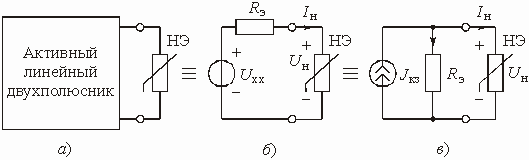
Рис. 5.5

Напомним, что параметры эквивалентного генератора определяют следующим образом: – напряжение на зажимах активного линейного двухполюсника (АЛД) при отключенном НЭ; – эквивалентное сопротивление пассивного двухполюсника, когда все задающие напряжения и токи источников АЛД равны нулю; – ток АЛД при коротком замыкании его зажимов.

Ток в НЭ и напряжение на нем находятся из системы, состоящей всего из двух уравнений. Так, применяя закон напряжений Кирхгофа (ЗНК) к схеме рис. 5.5, б, получаем:

. (5.2)

Дописывая к данному равенству уравнение НЭ , получаем систему из двух уравнений. Решить данную систему можно графическим путем, построив график прямой

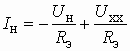(5.3)

и график ВАХ нелинейного элемента. Точка пересечения графиков дает значение тока и напряжения на НЭ (рис. 5.6).

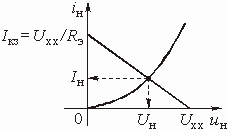
Рис. 5.6

Все остальные токи и напряжения на линейных элементах можно найти, используя законы Кирхгофа.

Пример 5.1

Рассчитать ток, протекающий через нелинейный элемент в цепи, изображенной на рис. 5.7 Заданы: ВАХ НЭ (рис. 5.8), = 2 кОм, U = 1 В, = = 0,5 мА.

Для построения прямой (5.3) рассчитаем напряжение холостого хода между узлами 1 и 2 (при отключении НЭ), эквивалентное сопротивление пассивного двухполюсника и ток короткого замыкания (при закороченном НЭ):

2 В;

2 кОм;

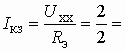1 мА.

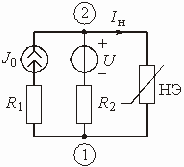
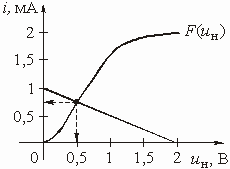
Рис. 5.7                                Рис. 5.8

Строим график прямой (5.2) по аналогии с графиком, изображенным на рис. 5.6. Точка пересечения этой прямой с ВАХ НЭ (рис. 5.8) дает значения тока 0,7 мА, протекающего через НЭ, и напряжения = 0,5 В на нем.

Для расчета цепи, содержащей несколько НЭ, используют эквивалентные преобразования схемы. Суть эквивалентных преобразований состоит в замене участков цепи с параллельным или последовательным соединением ветвей одной эквивалентной ветвью путем суммирования их токов или напряжений. Речь здесь идет о суммировании ординат или абсцисс заданных характеристик ветвей цепи. Этот метод особенно эффективен в случае цепи с одним источником: цепь представляется источником и одним эквивалентным нелинейным элементом.

Пусть два НЭ с уравнениями (ВАХ) и включены параллельно (рис. 5.9). Поскольку приводимые ниже рассуждения справедливы не только для режима постоянного, но и для режима переменного тока, в дальнейшем будем использовать для обозначений напряжений и токов малые (строчные) буквы.

Необходимо найти уравнение НЭ, эквивалентного данному соединению элементов. Так как элементы соединены параллельно, то , а по первому закону Кирхгофа . Выполним сложение токов графически, как показано на рис. 5.10. Задаемся значением напряжения. При этом значении напряжения находим токи НЭ и суммируем их. Задаемся новым значением напряжения и опять суммируем токи. Таким образом, находим серию точек, соединяя которые, получаем ВАХ эквивалентного НЭ.

         

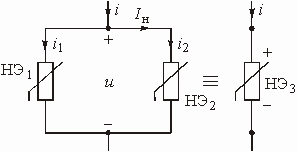
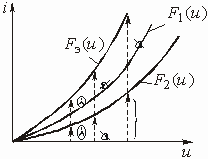
Рис. 5.9                                                Рис. 5.10

           

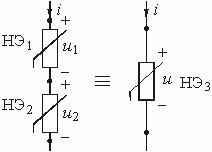
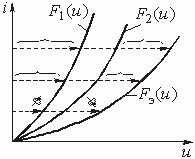
Рис. 5.11                                      Рис. 5.12

Рассмотрим последовательное соединение НЭ (рис. 5.11). В данном случае , а . Процесс определения ВАХ НЭ показан на рис. 5.12. Заметим, что рассмотренные преобразования применимы и в случае, когда последовательно или параллельно соединены несколько нелинейных, а также линейных элементов.

Пример 5.2

Рассчитать напряжения и токи в цепи, схема которой изображена на рис. 5.13, где U = 5 В, R = 500 Ом, а ВАХ НЭ заданы графиками на рис. 5.14.

Поскольку ВАХ заданы графиками, то при решении воспользуемся графическими построениями. Найдем ВАХ двухполюсника, эквивалентного параллельному соединению линейного сопротивления R и НЭ₂. Для этого перенесем ВАХ НЭ₂ на новый рисунок и построим ВАХ линейного элемента (рис. 5.15, а). На этом же рисунке показана эквивалентная ВАХ . Перенесем эту эквивалентную ВАХ и ВАХ НЭ₁ на рис. 5.15, б и найдем ВАХ эквивалентного двухполюсника , который присоединяется к зажимам источника.

         

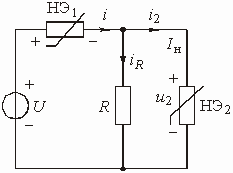
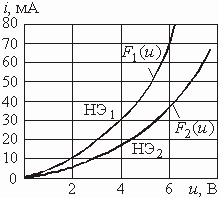
Рис. 5.13                                        Рис. 5.14

           

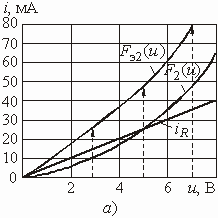
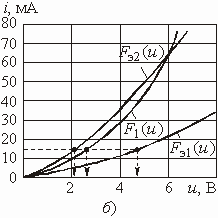
Рис. 5.15

По рис. 5.15, б по кривой находим, что напряжению u = 5 В соответствует ток i = 16 мА, по кривой – напряжение на НЭ₁ = 2,8 В и по кривой – напряжение на параллельном соединении R и НЭ₂ = 2,2 В. Зная это напряжение, по графикам рис. 5.15, a находим = 11 мА и = 5 мА.

Пример 5.3

 

На рис. 5.16, а показана подключенная к источнику напряжения цепь из трех резистивных НЭ. Суммирование ординат характеристик элементов 2 и 3, соединенных параллельно, дает эквивалентную характеристику 2 – 3 (рис. 5.16, б). Суммируя абсциссы последней с абсциссами кривой 1, получаем эквивалентную характеристику нелинейной цепи . Из графиков рис. 5.16, б можно, задаваясь напряжением на входе, получить токи и напряжения ветвей.

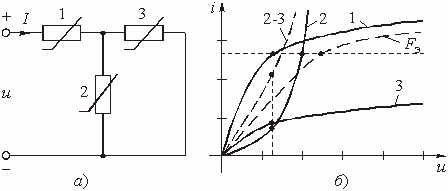
Рис. 5.16

Если вольт-амперные характеристики двухполюсных НЭ заданы не графически, а аналитически, причем функции достаточно простые, то для расчета нелинейных цепей составляют систему уравнений состояния цепи, которую решают аналитически или численными методами.

Уравнения состояния цепи обычно составляют на основании законов Кирхгофа. Методика составления уравнений остается такой же, как и в случае линейных резистивных цепей, но дополнительно появляются уравнения вида для НЭ.

Составим, например, систему уравнений состояния для цепи, схема которой изображена на рис. 5.17. Пусть ВАХ нелинейного элемента описывается выражением

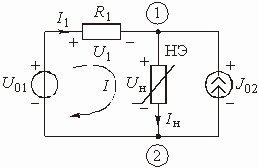
Рис. 5.17

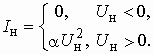(5.4)

Зададимся положительными направлениями напряжений и токов. Цепь содержит один независимый контур (I) и один независимый узел (1). Уравнения, записанные по закону токов Кирхгофа (ЗТК) и ЗНК, имеют следующий вид:

; (5.5)

. (5.6)

К этим уравнениям дописываем уравнение (5.4). Неизвестными в данной системе уравнений являются напряжение и токи и . Всего три неизвестных. Для их отыскания составлено три уравнения. Как видим, процесс составления системы уравнений такой же, как и в случае линейной цепи. Однако процесс решения полученной системы, которая содержит нелинейное уравнение, может существенно затрудниться. Для большинства относительно сложных цепей аналитического решения системы уравнений может и не существовать. Тогда приходится прибегать к численным методам решения.

Пример 5.4

Рассчитать ток и напряжение на нелинейном элементе, а также ток в цепи, изображенной на рис. 5.17, если заданы значения = 1 кОм, = 14 В, = = 10 мА, А/В.

Предположим вначале, что решение системы уравнений (5.5), (5.6), (5.4) существует при . Тогда уравнение НЭ имеет вид

. (5.7)

Выразим из уравнения (5.5) ток и подставим его в уравнение (5.6). В результате этой операции получим

. (5.8)

Подставив в (5.8) выражение (5.7), получим уравнение относительно неизвестного напряжения на нелинейном двухполюснике

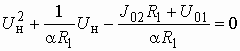. (5.9)

Отсюда имеем

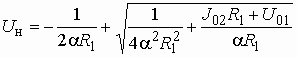. (5.10)

Подставляя в (5.10) заданные значения , , и , получаем = 20 В.

Второе решение уравнения (5.9) даст . Это решение не подходит, так как применялось уравнение НЭ, справедливое при .

Допустим теперь существование решения системы уравнений (5.5) – (5.6) при . Согласно уравнению НЭ (5.4) . Тогда из уравнения (5.8) имеем

24 В > 0,

а это противоречит условию, что .

Таким образом, остается первое решение (5.10). Найдем остальные неизвестные. Из (5.7) имеем = мА, а из (5.5) –6 мА.

В данном примере получено аналитическое решение системы нелинейных уравнений. Если бы ВАХ нелинейного элемента описывалась более сложной функцией, то этого достичь не удалось бы.

Можно составлять уравнения состояния цепи методом узловых напряжений (потенциалов).

Рассмотрим в качестве примера схему, изображенную на рис. 5.18. Пусть ВАХ нелинейных элементов описываются выражениями для элемента НЭ₁ и для элемента НЭ₂. В схеме имеется зависимый источник (ИТУТ) с током .

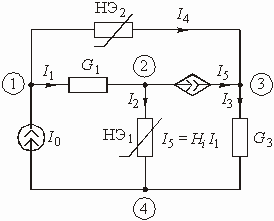
Рис. 5.18

Приняв узел 4 за базисный, имеем три независимых узла: 1, 2 и 3. Токи ветвей выражаются через узловые напряжения , и следующим образом:

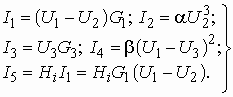(5.11)

Составим уравнения для узлов 1, 2 и 3 по ЗТК:

;

;

.

Подставив в эти уравнения значения токов из (5.11), получим

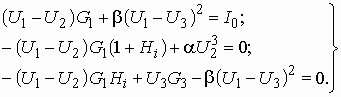(5.12)

Уравнения узловых напряжений получены в виде системы трех нелинейных уравнений с тремя неизвестными узловыми напряжениями. Можно уменьшить число уравнений, если из первого уравнения выразить через и и исключить его из двух остальных уравнений. В результате получим систему двух нелинейных уравнений с двумя неизвестными напряжениями узлов 1 и 3.

Решить данную систему уравнений можно одним из численных методов (например, известным из математики методом Ньютона – Рафсона). Определив узловые напряжения, можно вычислить токи и напряжения ветвей.

Рассмотрим порядок расчета резистивных цепей, если в их состав входят нелинейные четырехполюсники, которые описываются нелинейными уравнениями, связывающими напряжения и токи на его входе (, ) и выходе (, ):

;

.

На рис. 5.19 показана схема включения нелинейного четырехполюсника, а на рис. 5.20 – семейство его входных (а) и выходных (б) ВАХ.

По ЗНК для входной и выходной цепей схемы рис. 5.19 можно записать:

и .

Рис. 5.19

Решая эти уравнения относительно токов и , получаем уравнения

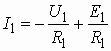и ,

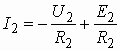которые называются уравнениями нагрузочных прямых.

На рис. 5.20 построены графики этих прямых и графических входных и выходных ВАХ четырехполюсного НЭ. Точки пересечения нагрузочных прямых и ВАХ определяют режимы постоянного тока (рабочие точки) на входе и выходе четырехполюсного НЭ.

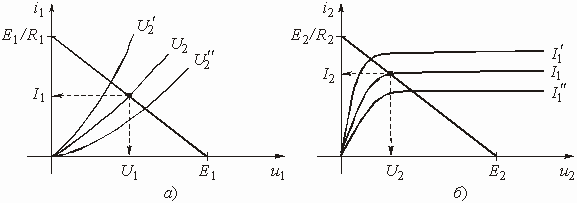
Рис. 5.20

Как правило, ВАХ нелинейных элементов получают экспериментально, поэтому чаще всего они заданы в виде таблиц или графиков. Чтобы иметь дело с аналитическими выражениями, приходится прибегать к аппроксимации.

На рис. 5.21 приведена ВАХ нелинейного элемента. Пусть к нелинейному элементу приложено постоянное напряжение и гармоническое напряжение .

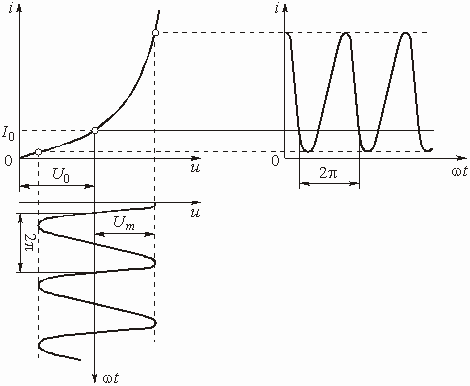
Рис. 5.21

Увеличение величины постоянного напряжения приведет к смещению на рис. 5.21 гармонического напряжения вправо, а уменьшение – к смещению гармонического напряжения влево. В связи с этим постоянное напряжение назвали напряжением смещения, а точку на ВАХ с координатами (,) – рабочей точкой. Таким образом, выбор рабочей точки на ВАХ связан с изменением напряжения смещения .

При подаче на нелинейный элемент гармонического напряжения рабочая точка будет перемещаться по ВАХ в такт с изменением мгновенного значения гармонического напряжения.

Очевидно, что аппроксимировать (т. е. описывать аналитически) нужно только тот участок ВАХ, по которому перемещается рабочая точка.

Часто в качестве аппроксимирующего ВАХ выражения используют степенной полином:

. (5.13)

Определить коэффициенты , , ... , полинома (5.13) можно различными способами. Наиболее распространенным способом является интерполяция (метод выбранных точек), при которой коэффициенты , , ... , находятся из равенства значений полинома (5.13) и аппроксимируемой ВАХ в выбранных точках (узлах интерполяции).

Пример 5.5

Аппроксимировать экспериментальную зависимость тока базы от напряжения между базой и эмиттером для биполярного транзистора, заданную в таблице 5.1.

                                                           Таблица 5.1

, В	0,4	0,5	0,6	0,7	0,8	0,9
, мА	0,05	0,07	0,1	0,175	0,3	0,53

Известно также, что напряжение смещения и что амплитуда гармонического напряжения на входе транзистора не превышает 0,2 В, т. е. Ф 0,2 В.

Экспериментальные точки из табл. 5.1 показаны на графике рис. 5.22 кружочками, соединенными пунктиром.

Можно потребовать, чтобы значения степенного полинома совпадали со значениями тока для всех шести значений напряжения , указанных в таблице. В этом случае необходимо выбрать степенной полином 5-ой степени (т.к. он содержит 6 коэффициентов).

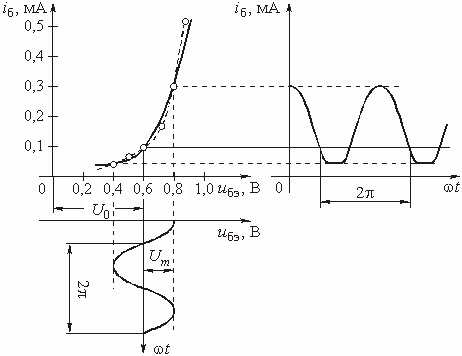
Рис. 5.22

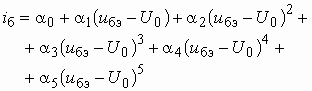(5.14)

и составить систему уравнений. Первое уравнение получаем, подставляя в (5.14) значения и :

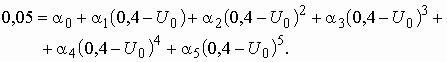
Второе уравнение получаем, подставляя в (5.14) значения и :

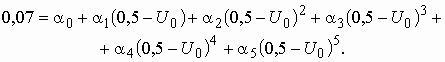
Третье уравнение получаем, подставляя в (5.14) значения и :

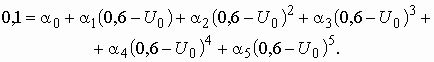
Четвертое уравнение получаем, подставляя в (5.14) значения и :

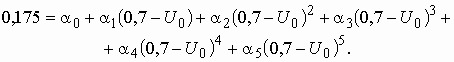
Пятое уравнение получаем, подставляя в (5.14) значения и :

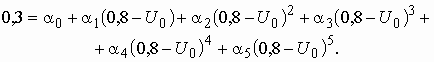
И, наконец, шестое уравнение получаем, подставляя в (5.14) значения и :

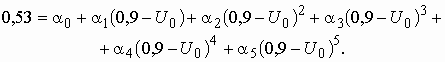
Учитывая, что , получим окончательно следующую систему:

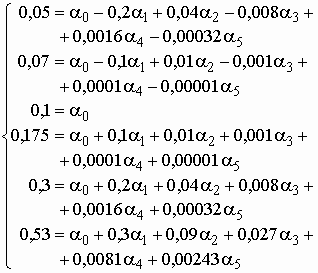(5.15)

Решение системы уравнений (5.15) даст искомые значения коэффициентов , , , , и , при которых ток базы (5.14) будет совпадать во всех узлах интерполяции со значениями тока из Табл. 5.1. По формуле (5.14) можно вычислить любые промежуточные значения тока и построить точный график аппроксимирующей функции.

Заметим, что решение системы уравнений, состоящей из 6-ти уравнений с 6-ю неизвестными, в настоящее время не представляет заметных трудностей. Для этих целей существуют программы не только для персональных компьютеров, но и для микрокалькуляторов.

Однако, нет необходимости аппроксимировать ВАХ вне интервала 0,4 В Ф Ф 0,8 В, так как мы знаем, что сигнал на входе транзистора не выходит за эти пределы (действительно, и ). Кроме того, можно выбрать меньше узлов интерполяции (например, ; 0,6 В; 0,8 В), что позволит уменьшить степень аппроксимирующего полинома до 2-ой:

.

Система уравнений будет состоять всего из 3-х уравнений и содержать 3 неизвестных:

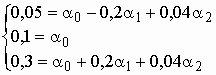
Решение этой системы дает , 0,625 мА/В, . Кривая тока

(5.16)

                                                                 Таблица 5.2

, В	0,4	0,5	0,6	0,7	0,8	0,9
Значения , мА из (5.16)	0,05	0,05625	0,1	0,18125	0,3	0,45625

проходит через три экспериментальные точки (рис. 5.22).

В табл. 5.2 приведены для сравнения значения тока базы вычисленные из (5.16). Из рисунка и таблиц видно, что экспериментальные точки достаточно плотно “ложатся” на кривую (5.16).

Прежде всего следует уточнить, что понимается под большой амплитудой гармонического напряжения. На рис. 5.23 кружочками, соединенными пунктирной линией, показана экспериментальная зависимость тока базы от напряжения , полученная для транзистора КТ-306. Кроме того, известно, что напряжение смещения выбрано равным , а гармонический сигнал, также подводимый к нелинейному элементу, имеет амплитуду (рис. 5.23).

Из графика видно, что когда мгновенное значение гармонического напряжения изменяется от –0,3 до –0,6 В, напряжение на участке “база – эмиттер” становится отрицательным и ток базы отсутствует ( = 0), т. е. транзистор “закрыт”. По-видимому, в данном случае как раз и можно говорить о большой амплитуде сигнала на входе транзистора.

С некоторым приближением можно считать, что ВАХ транзистора имеет два участка: первый – там, где ток базы = 0 (при ) и транзистор “закрыт”; второй – там, где ток базы растет с ростом напряжения и, следовательно, транзистор “открыт” . При этом можно пренебречь “кривизной” вольт-амперной характеристики и заменить ее на втором участке прямой линией. На рис. 5.23 аппроксимирующая ВАХ прямая линия изображена сплошной линией. Такой же сплошной линией показана зависимость тока базы от времени, полученная путем проекции гармонического напряжения на аппроксимирующую ВАХ прямую линию. Для сравнения пунктиром показан реальный ток базы, протекающий через нелинейный элемент с экспериментальной ВАХ. Поскольку отличие этих кривых незначительное, можно считать замену ВАХ прямой линией вполне приемлемой.

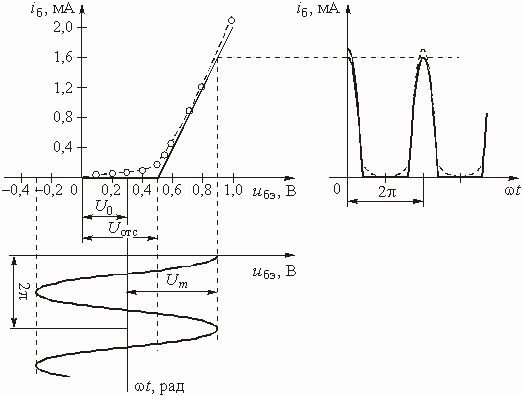
Рис. 5.23

Уравнение прямой линии имеет вид: , где К – коэффициент, определяющий наклон прямой. Смещение прямой параллельно самой себе вправо оси абсцисс на величину описывается выражением:

.

Наклон аппроксимирующей ВАХ прямой линии определяется крутизной S, а смещение по оси – напряжением отсечки . Аппроксимирующая ВАХ функция задается параметрически для двух участков напряжения (рис. 5.23):

(5.17)

Для экспериментальных данных, приведенных на рис. 5.23, крутизна S определяется приращением тока к приращению напряжения и составляет 4 мА/В, а напряжение отсечки равно 0,5 В.

Пример 5.6

Аппроксимировать график зависимости тока стока от напряжения между затвором и истоком для полевого транзистора (рис. 5.24), на вход которого подается напряжение , В.

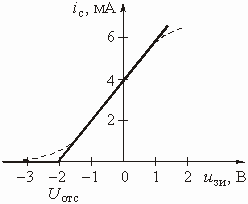
Рис. 5.24

Транзистор работает в режиме большого сигнала, поэтому его ВАХ аппроксимируется двумя прямыми линиями. По графику находим напряжение отсечки = –2 В. По аналогии с (5.17) в диапазоне изменения напряжения Ф –2 В ток стока равен нулю. Когда напряжение становится больше , то крутизна S аппроксимирующей прямой рассчитывается по формуле

.

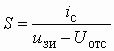Подставляя в эту формулу значения и на границе рабочего диапазона, т. е. = 0, = 4 мА, получаем S = 2 мА/В.

Таким образом, аппроксимирующая ВАХ функция имеет вид

или

Рассмотрим схему усилительного каскада на биполярном транзисторе (рис. 5.25), на входе которого действует напряжение , состоящее из напряжения смещения и гармонического напряжения с амплитудой . Под действием входного напряжения в цепи коллектора транзистора протекает коллекторный ток . Зависимость коллекторного тока от напряжения на участке “база – эмиттер” является проходной вольт-амперной характеристикой.

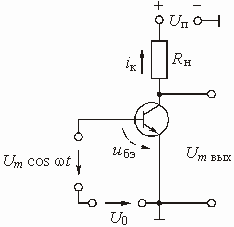
Рис. 5.25

На рис. 5.26 изображены проходная ВАХ транзисторного каскада, зависимость во времени напряжения на входе каскада и зависимость во времени коллекторного тока . Напряжение смещения и амплитуда гармонического напряжения выбраны на рисунке таким образом, что рабочая точка не выходит за пределы линейного участка ВАХ. В результате коллекторный ток будет содержать постоянную составляющую и гармоническую составляющую с амплитудой .

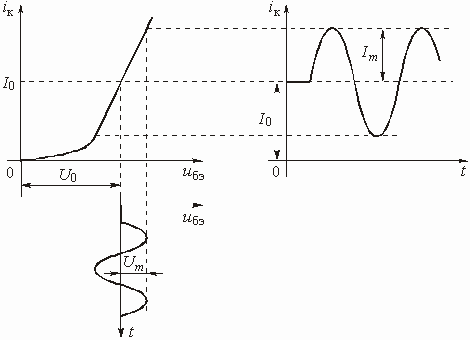
Рис. 5.26

Иная картина будет наблюдаться, если напряжение смещения уменьшить и, тем самым, выбрать рабочую точку на нижнем, нелинейном, участке ВАХ (рис. 5.27). Форма тока исказится, ток перестанет быть гармоническим. Дальнейшее уменьшение напряжения смещения приведет к еще большему искажению формы тока (рис. 5.28).

Из теории спектрального анализа сигналов известно, что любой периодический сигнал может быть представлен рядом Фурье. Это значит, что коллекторный ток складывается из постоянной составляющей, основной составляющей с частотой входного сигнала и высших гармоник:

. (5.18)

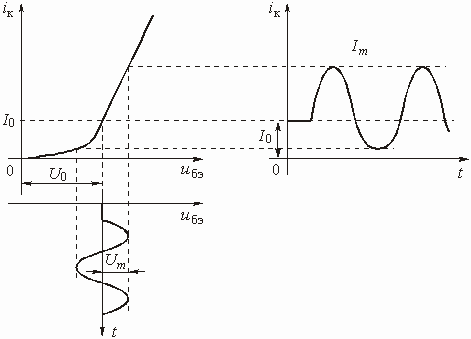
Рис. 5.27

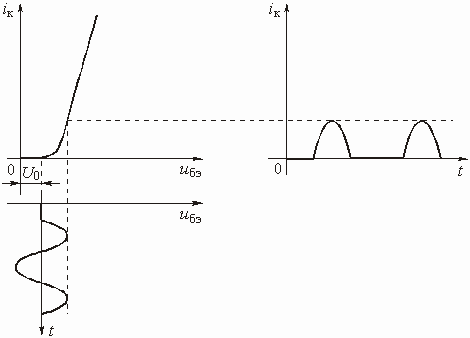
Рис. 5.28

Искажения формы сигнала из-за нелинейности ВАХ называют нелинейными искажениями. Если перед нами стоит задача усилить сигнал без искажений (например, при воспроизведении речи, музыки, изображения и т. п.), то следует выбирать такой режим работы (напряжение смещения и амплитуды сигналов), чтобы не выходить за пределы линейного участка ВАХ.

Наоборот, стремление преобразовать сигнал с помощью нелинейного элемента, например, не дать мгновенному значению сигнала превысить некоторый заранее установленный порог, приводит к необходимости работать в режиме больших нелинейных искажений.

На рис. 5.29 изображена вольт-амперная характеристика диода. Приближенно можно считать, что при воздействии на диод напряжения в “прямом направлении” (правая полуплоскость рисунка) через него будет протекать ток, т. е. р-n переход диода будет открыт, а при воздействии напряжения в “обратном направлении” (левая полуплоскость рисунка) ток практически протекать не будет, т. е. p-n переход диода будет закрыт.

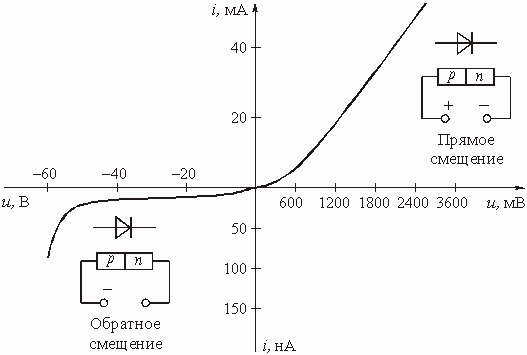
Рис. 5.29

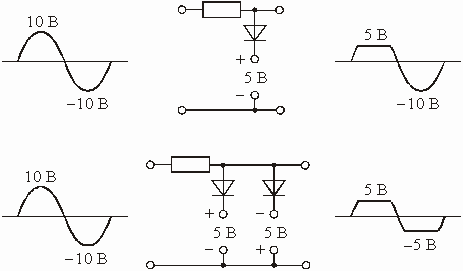
Рис. 5.30

На практике широко применяются схемы диодных ограничителей напряжения (рис. 5.30). Здесь диод выполняет роль вентиля: в открытом состоянии его сопротивление мало (десятки Ом), в закрытом состоянии – очень велико (сотни МОм). Эти свойства диода позволяют аппроксимировать его ВАХ кусочно-линейной функцией (рис. 5.31). Напряжением смещения регулируют порог ограничения.

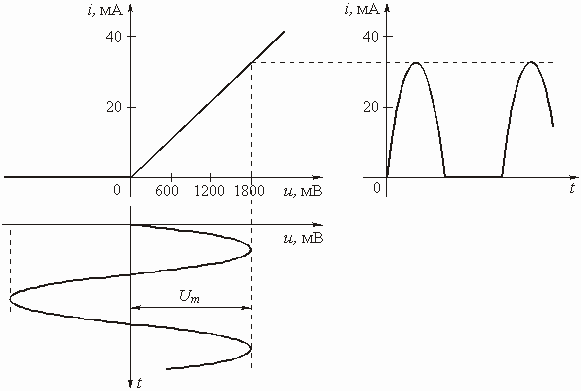
Рис. 5.31

Ограничимся рассмотрением полиномов со степенью не выше третьей.

График полинома первой степени

(5.19)

представляет собой прямую , параллельную оси абсцисс, и наклонную прямую с коэффициентом наклона , смещенную по оси абсцисс на величину . Регулируя величины , и , можно перемещать аппроксимирующую прямую вниз, вправо и влево и менять ее наклон.

Для определения амплитуд гармоник тока подставим в (5.19) выражение для напряжения, приложенного к нелинейному элементу :

.

Сравнивая это выражение с рядом Фурье

,

видим, что ; ; . Таким образом, при аппроксимации ВАХ полиномом 1-ой степени ток содержит кроме постоянной составляющей только основную (первую) гармонику, совпадающую по частоте с приложенным гармоническим напряжением. Высшие гармоники в спектре тока отсутствуют, нелинейных искажений нет.

График полинома второй степени

(5.20)

содержит в дополнение к графику полинома первой степени квадратичную параболу , смещенную по оси абсцисс на величину . Квадратичный член служит для аппроксимации слабой нелинейности ВАХ параболического типа.

Подставляя в (5.20) напряжение , получим:

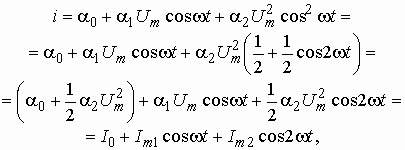
Это выражение показывает, что если вольт-амперная характеристика нелинейного элемента имеет нелинейность, описываемую квадратичной параболой, то в спектре тока, протекающего через такой нелинейный элемент, появляется при воздействии на него постоянного и гармонического напряжений вторая гармоника с частотой 2w .

Для описания нелинейности ВАХ более высокого порядка используется полином третьей степени

, (5.21)

в котором добавляется так называемая кубическая парабола , смещенная по оси абсцисс на величину .

В этом случае подстановка напряжения в
(5.21) дает:

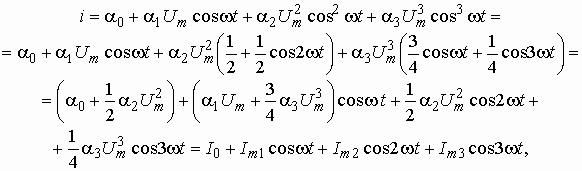
где постоянная составляющая и амплитуды гармоник , и .

Из приведенных примеров видно, что наличие в ВАХ нелинейностей высокого порядка приводит к появлению высших гармоник в спектре тока. Количество гармоник в спектре тока равно степени полинома, описывающего нелинейность ВАХ. Постоянная составляющая и амплитуды четных гармоник определяются коэффициентами полинома при четных степенях, а амплитуды нечетных гармоник – коэффициентами полинома при нечетных степенях. Это означает, что если ВАХ аппроксимируется полиномом только с четными степенями, в спектре тока будут присутствовать постоянная составляющая и четные гармоники. При аппроксимации ВАХ полиномом с нечетными степенями спектр тока будет содержать только нечетные гармоники.

Пример 5.7

Рассчитать спектральный состав тока базы биполярного транзистора для данных Примера 5.5. Построить спектр тока.

В рабочем диапазоне напряжений 0,4 В Ф Ф 0,8 В ВАХ транзистора была аппроксимирована полиномом
2-ой степени (5.20)

.

Коэффициенты полинома были определены в Примере 5.5 (см. формулу (5.16)):

= 0,1 мА; = 0,625 мА/В; = 1,875 мА/В².

Рассчитаем значения постоянной составляющей и амплитуды первой и второй гармоник тока, воспользовавшись вышеприведенными формулами:

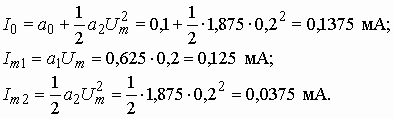
Спектр тока (рис. 5.32) содержит постоянную составляющую и две гармоники с амплитудами и .

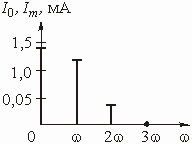
Рис. 5.32

Напомним, что при больших амплитудах гармонического напряжения, подводимого к нелинейному элементу, практически нет смысла учитывать небольшую кривизну ВАХ (так называемую слабую нелинейность). В тех случаях, когда нелинейный элемент работает как вентиль: есть ток или нет тока, используют кусочно-линейную аппроксимацию ВАХ (рис. 5.33):

(5.21)

График тока при этом имеет вид косинусоидальных импульсов с отсечкой. Половина той части периода в радианах (или градусах), в течение которой протекает ток, называется углом отсечки и обозначен на рисунке буквой q .

Из графика рис. 5.33 можно вычислить угол отсечки q . При напряжение . Откуда

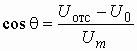и 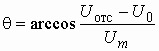. (5.22)

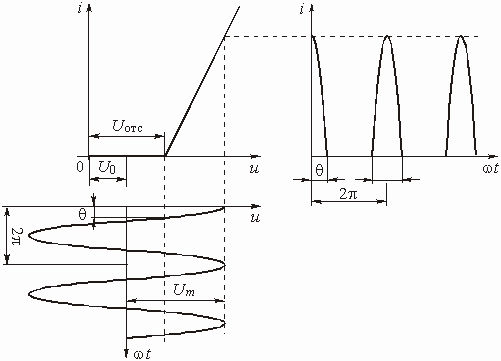
Рис. 5.33

Последнее равенство показывает, что угол отсечки можно изменить, меняя напряжение смещения , амплитуду гармонического сигнала или выбирая параметр аппроксимирующей функции (5.21).

Периодическую последовательность импульсов тока на рис. 5.33 можно разложить в ряд Фурье:

.

Опуская процедуру нахождения коэффициентов ряда Фурье и отсылая любознательного читателя к стандартным учебникам, приведем окончательный результат.

Постоянная составляющая и амплитуды гармоник тока вычисляются по формуле

, k = 0, 1, 2, 3, ... , (5.23)

где функции называются функциями Берга (в честь крупного российского радиотехника академика А.И. Берга). Они зависят от угла отсечки и их значения для разных углов отсечки приводятся в справочниках. Графики нескольких функций Берга представлены на рис. 5.34.

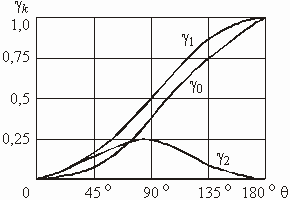
Рис. 5.34

Чтобы получить максимальные амплитуды гармоник, следует выбирать , так как при таких углах отсечки функции Берга принимают максимальные значения.

Таким образом, амплитуды спектральных составляющих тока в нелинейном элементе при кусочно-линейной аппроксимации его ВАХ зависят от угла отсечки. Количество гармоник при этом бесконечно большое. Чем меньше угол отсечки (т. е. чем уже импульс), тем медленнее убывают амплитуды гармоник тока.

Пример 5.8

Рассчитать постоянную составляющую и амплитуды первой и второй гармоник в спектре тока стока полевого транзистора для данных Примера 5.6.

По данным Примера 5.6 напряжение смещения = –3 В, амплитуда гармонического напряжения = 3 В, напряжение отсечки = –2 В, крутизна S = 2 мА/В.

По формуле (5.22) рассчитываем угол отсечки:

.

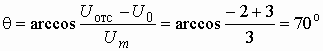Для угла отсечки определяем по графикам, приведенным на рис. 5.34, функции Берга:

, .

Постоянную составляющую и амплитуды гармоник тока рассчитываем, используя формулу (5.23):

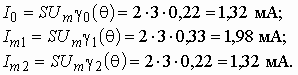
Амплитуды других гармоник в спектре тока можно рассчитать аналогично, выбрав в справочнике соответствующие функции Берга.

Рассмотрим вначале процессы в линейном усилителе с резистивной нагрузкой (рис. 5.35, а). Это позволит лучше уяснить отличия от него нелинейного резонансного усилителя. Будем полагать, что ВАХ , т. е. зависимость тока коллектора от напряжения на участке база–эмиттер, достаточно точно представляется кусочно-линейной функцией вида (5.21). На входе НЭ транзистора действует напряжение

,

не выходящее за пределы линейного участка. Тогда ток в цепи коллектора

будет, как и входное напряжение, гармоническим (рис. 5.35, б).

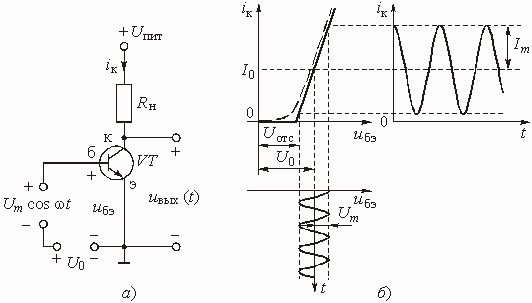
Рис. 5.35

Определим коэффициент полезного действия (КПД) линейного усилителя. Ток коллектора создает на резисторе нагрузки падение напряжения , которое является выходным сигналом с амплитудой . КПД усилителя есть отношение полезной активной мощности

к активной мощности, потребляемой от источника питания , т. е.

.

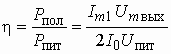Из рис. 5.35, б видно, что . Если при этом учесть, что , то получим КПД h Ф 0,5, т. е. коэффициент полезного действия линейного усилителя не может превышать 50%.

Вольт-амперная характеристика реальных транзисторов является нелинейной (на рис. 5.35, б она показана штрихами), поэтому форма тока в цепи коллектора при гармоническом воздействии на усилитель будет отличаться от гармонической. В коллекторной цепи оказываются постоянная составляющая, а также первая, вторая и последующие гармоники частоты сигнала.

Чтобы количественно оценить степень искажения сигнала на выходе усилителя, вводят коэффициент гармоник, который определяется отношением среднеквадратического уровня всех высших гармоник к амплитуде первой гармоники тока:

.

Пример 5.9

Рассчитать коэффициент гармоник усилителя на биполярном транзисторе, спектр тока базы которого был рассчитан в Примере 5.7.

ВАХ транзистора была аппроксимирована полиномом 2-ой степени, поэтому в спектре тока есть только постоянная составляющая = 0,1375 мА и две гармоники, имеющие амплитуды = 0,125 мА и = 0,0375 мА. Коэффициент гармоник рассчитаем, воспользовавшись формулой (5.24):

.

Так работает усилитель в линейном режиме, который в большинстве случаев и используется на практике. Между тем, достаточно мощные усилители выгодно использовать в нелинейном режиме работы, поскольку, как будет показано ниже, они имеют более высокий КПД.

Нелинейный резонансный усилитель изображен на рис. 5.36. На входе его действует переменное напряжение и постоянное напряжение смещения , причем амплитуда переменного напряжения велика, так что напряжение “выходит” за рамки линейного участка (см. рис. 5.33). Ток в цепи коллектора имеет форму косинусоидальных импульсов с отсечкой. Резонансный контур настроен на частоту первой гармоники тока, т. е. на частоту входного сигнала w . Сопротивление параллельного контура на этой частоте велико, а на частотах гармоник 2w , 3w , ... мало, так что высшие гармонические составляющие практически не влияют на форму выходного сигнала и

,

где – амплитуда первой гармоники тока коллектора . – сопротивление параллельного контура на резонансной частоте w .

           

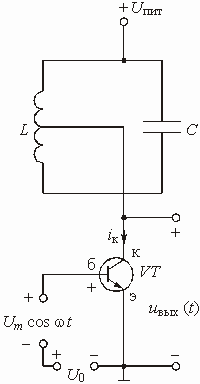
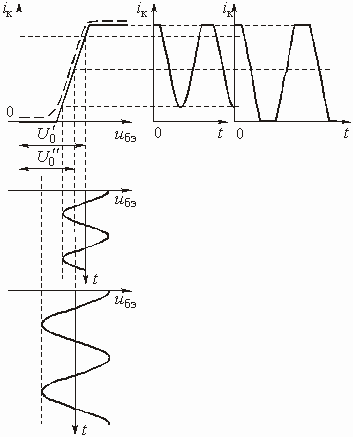
Рис. 5.36                                                               Рис. 5.37

Выходное напряжение

практически оказывается косинусоидальным (т. е. гармоническим).

Вычислим КПД нелинейного резонансного усилителя. Мощность, потребляемая от источника, . Полезная активная мощность в колебательном контуре

.

Отсюда

.

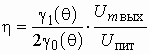В мощных усилителях обычно стремятся максимально использовать источник питания и получают , поэтому КПД

.

Исследования показывают, что с уменьшением q отношение растет, т. е. КПД увеличивается, но одновременно падает амплитуда первой гармоники. Считается, что оптимальным значением является q = 90° , при этом отношение функций Берга равно 1,517. Это соответствует КПД около 76%.

Таким образом, нелинейный резонансный усилитель работает в более выгодном энергетическом режиме по сравнению с линейным усилителем.

Пример 5.10

Рассчитать КПД резонансного усилителя, если угол отсечки q = 70° (см. Пример 5.8).

В Примере 5.8 по графикам рис. 5.34 были определены значения функций Берга:

КПД нелинейного резонансного усилителя

.

Схема резонансного умножителя частоты отличается от нелинейного резонансного усилителя (см. рис. 5.36) только тем, что колебательный контур в выходной цепи настраивается на частоту одной из высших гармоник входного сигнала.

Амплитуда выходного сигнала умножителя при кусочно-линейной аппроксимации равна

,

а выходной сигнал

имеет частоту в k раз больше, чем у входного сигнала

.

При больших k функции имеют небольшие значения, поэтому важно выбрать угол отсечки q , при котором значение соответствующей функции Берга максимально. Существует оптимальный угол отсечки , при котором амплитуда выходного напряжения получается наибольшей.

Умножители частоты применяются в радиотехнике для получения высокочастотных стабильных колебаний, когда в распоряжении имеется стабильный низкочастотный генератор. Если отклонение частоты w , генерируемое низкочастотной схемой, составляет D w , то относительная нестабильность частоты равна D w /w . В умножителе частоты вместо частоты w + D w получаем частоту k(w + D w ), а относительная нестабильность kD w /kw остается такой же, как и у низкочастотного генератора.

К ограничителям мгновенных значений предъявляются следующие требования. Если мгновенное значение входного сигнала превышает заданное значение, называемое порогом ограничения, то значение выходного сигнала должно оставаться неизменным. Различают ограничения снизу, сверху и двухстороннее. Ограничение снизу наглядно демонстрирует рис. 5.33. Таким образом, в схеме на транзисторе можно совмещать функции усилителя и ограничителя, если амплитуда входного сигнала “выходит” за рамки линейного участка ВАХ (см. рис. 5.33), а в цепи коллектора включена резистивная нагрузка (см. рис. 5.35, а). Порог ограничения можно регулировать напряжением смещения .

Ограничение сигнала сверху и двухстороннее ограничение можно также осуществить на транзисторном резистивном каскаде (см. рис. 5.35, а), если ВАХ будет иметь вид, показанный на рис. 5.37. Ограничение происходит за счет верхней отсечки тока, двухстороннее ограничение – за счет нижней и верхней отсечки тока . Указанная характеристика транзистора получается при использовании существенно пониженного напряжения коллекторного питания . Идеализация характеристики достигается применением кусочно-линейной аппроксимации тремя отрезками прямых.

Пример 5.11

На вход усилителя (рис. 5.35, а) поступает напряжение . Проходная ВАХ транзистора изображена на рис. 5.38 пунктиром. Построить график тока .

Аппроксимируем ВАХ транзистора тремя отрезками прямых. Усилитель работает в режиме двухстороннего ограничения тока. График тока построен, используя метод проекций, и приведен на рис. 5.38.

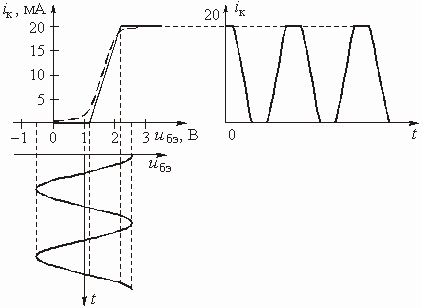
Рис. 5.38

Ограничители мгновенных значений могут строиться на схемах с диодами, ВАХ которых могут быть также аппроксимированы отрезками прямых. На рис. 5.39 приведены схемы диодных ограничителей снизу (а), сверху (б) и двухстороннего (в). В этих схемах сигнал появляется на выходе, если диод закрыт. Меняя величину пороговых напряжений, можно осуществлять ограничение на разных уровнях. Для правильной работы схемы необходимо, чтобы сопротивление резистора R было во много раз больше дифференциального сопротивления диода в открытом состоянии.

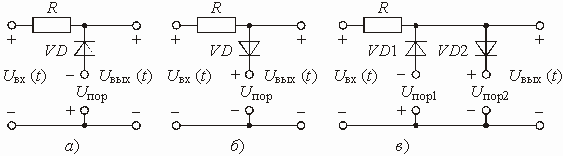
Рис. 5.39

Задача ограничителя амплитудных значений состоит в том, чтобы из сигнала с переменной амплитудой получить на его выходе колебание с постоянной амплитудой. Такая операция может быть выполнена с помощью нелинейного резонансного усилителя (см. рис. 5.36), работающего в режимах нижней и верхней отсечки тока. При этом будут получаться почти прямоугольные импульсы, подобные приведенным на рис. 5.37. Гармоническое же колебание с постоянной амплитудой выделяется колебательным контуром, настроенным на частоту сигнала w .

Ограничители мгновенных значений применяются, например, когда необходимо из синусоидального сигнала получить импульсы, близкие к прямоугольному. Ограничители амплитудных значений широко используются для устранения паразитных изменений амплитуды сигнала, которые могут возникнуть при передаче сигнала.

Подадим на вход цепи (рис. 5.40), состоящей из последовательного соединения диода и резистора , гармоническое напряжение. Когда подаваемое на диод напряжение таково, что его анод положителен по отношению к катоду, в цепи течет ток. Форма тока – синусоидальная в течение первой половины периода. Когда полярность напряжения меняется на противоположную, анод становится отрицательным по отношению к катоду, и тока в цепи нет.

Напряжение на резисторе пропорционально току и поэтому представляет собой последовательность однополярных синусоидальных импульсов. Этот процесс называется выпрямлением.

Приложенное напряжение изменяется по закону синуса; в первом полупериоде диод работает в режиме прямого смещения, а в следующем полупериоде – в режиме обратного смещения (см. рис. 5.29). Только при прямом смещении диода через него протекает ток. Падением напряжения на диоде в этот период времени пренебрегают.

Поскольку выпрямитель проводит ток только в течение одной половины периода приложенного напряжения, то и называется он полуволновым выпрямителем.

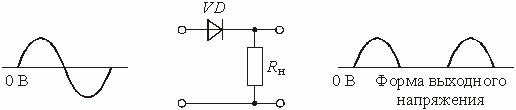
Рис. 5.40

Очевидно, что в выпрямителе, изображенном на рис. 5.40, выходное напряжение не является постоянным, как это требуется в цепях питания для электронной аппаратуры.

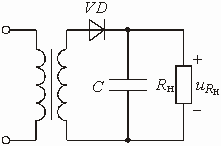
Рис. 5.41

Исследование формы сигнала показывает наличие пульсаций напряжения. Для того, чтобы сгладить эти пульсации и получить напряжение питания требуемого постоянного уровня, параллельно сопротивлению подключают емкость С (рис. 5.41), т. е. используют схему простейшего фильтра. Значение емкости должно быть большим (500 ё 5000 мкФ). Выпрямленные импульсы заряжают емкость до напряжения близкого к максимальному значению, создаваемому выпрямителем (рис. 5.42). Из-за больших значений емкости С постоянная времени будет тоже большой по сравнению с периодом приложенного напряжения.

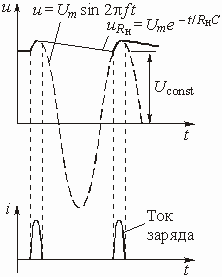
Рис. 5.42

Напряжение на сопротивлении поэтому уменьшается не по закону синуса, а по экспоненциальному закону в соответствии с уравнением

.

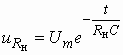Падение напряжения может быть уменьшено для данной нагрузки увеличением значения С.

Напряжение на выходе выпрямителя, когда используется один конденсатор, не является гладким, но может рассматриваться в виде малых пульсаций напряжения, наложенных на сравнительно большое постоянное напряжение . Это постоянное напряжение и является требуемым напряжением, а переменное пульсирующее напряжение должно быть устранено.

Чтобы уменьшить пульсации до приемлемого уровня, необходимо использовать селективный фильтр, который будет подавлять пульсирующее напряжение, но не будет значительно ослаблять постоянную составляющую. Схема такого фильтра приведена на рис. 5.43. Емкость представляет очень малое сопротивление переменным составляющим и очень большое сопротивление постоянной составляющей напряжения. Обычно используется емкость в несколько тысяч микрофарад. Амплитудно-частотная характеристика фильтра показана на рис. 5.44.

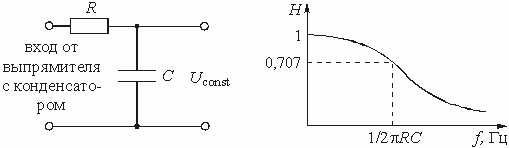
Рис. 5.43                                           Рис. 5.44

Схема двухполупериодного выпрямителя приведена рис. 5.45, а, график выпрямленного напряжения – на рис. 5.45, б.

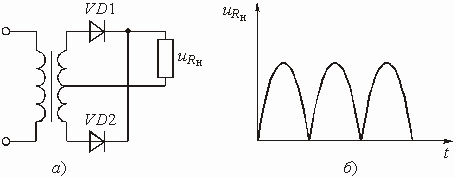
Рис. 5.45

Схема мостового выпрямителя с фильтром изображена на рис. 5.46.

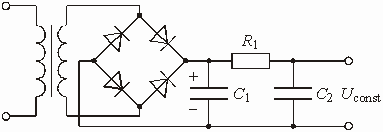
Рис. 5.46

Сигнал, состоящий из суммы двух гармонических колебаний с различными частотами и и амплитудами и

называется бигармоническим воздействием. Спектр бигармонического воздействия изображен на рис. 5.47, а.

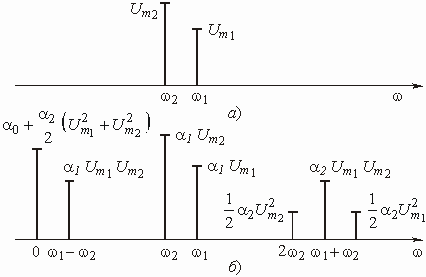
Рис. 5.47

Пусть на вход НЭ, ВАХ которого аппроксимирована полиномом второй степени

,

подано напряжение смещения и бигармонический сигнал . Подстановка напряжения в выражение для ВАХ позволяет определить ток в цепи НЭ в виде

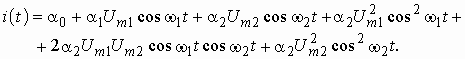
Используя тригонометрические формулы

и

,

получим

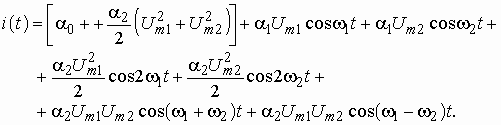(5.25)

Спектральный состав тока в цепи с НЭ показан на рис. 5.47, б.

                                                                                Таблица 5.3

Значения q	Частоты спектральных составляющих при значениях p
	0	1	2	3
0	w = 0
1				–
2			–	–
3		–	–	–

Принципиально новым по сравнению с воздействием на НЭ одного гармонического колебания здесь является появление спектральных составляющих с комбинационными частотами и . Если ВАХ нелинейного элемента аппроксимирована в общем случае полиномом степени N, то в спектральном составе тока будут присутствовать составляющие с комбинационными частотами , причем , где p и q – целые положительные числа (0, 1, 2, ...). Так, например, при аппроксимации ВАХ нелинейного элемента полиномом третьей степени в составе спектра тока присутствуют комбинационные частоты, приведенные в табл. 5.3.

В общем случае входное воздействие можно представить бесконечной суммой

.

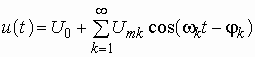В зависимости от степени N аппроксимирующего полинома (5.13) в спектре тока, протекающего через нелинейный элемент, появляются комбинационные частоты вида:

p, q, s, k – целые положительные числа. Например, при воздействии на НЭ с ВАХ в виде полинома второй степени суммы трех гармонических колебаний в спектре тока, помимо постоянной составляющей и первых двух гармоник каждой частоты, присутствуют комбинационные частоты ; ; . При аппроксимации полиномом третьей степени дополнительно появляются третьи гармоники , , и комбинационные частоты типа ; ; и т. д.

При передаче электрических сигналов на расстояние часто требуется переносить спектр сигнала вверх или вниз по шкале частот. Такой перенос спектра называется преобразованием частоты. Необходимость в преобразовании частот возникает, например, в случаях если спектр сигнала, который можно передать, расположен на шкале частот значительно ниже полосы пропускания системы передачи.

В качестве преобразователя частоты может быть использован усилительный каскад на транзисторе с колебательным контуром (рис. 5.48). Предположим, что нужно перенести вверх по шкале частот на значение w гармоническое низкочастотное колебание с частотой W :

.

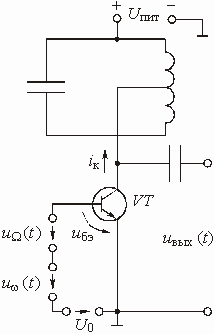
Рис. 5.48

Подадим на вход нелинейного резонансного усилителя, кроме этого колебания, также высокочастотное колебание с частотой w :

.

Амплитуды напряжений смещения , низкочастотного и высокочастотного колебаний выберем так, чтобы работать на участке ВАХ, который достаточно точно аппроксимируется полиномом второй степени

. (5.26)

Напряжение на участке база – эмиттер

.

После подстановки этого выражения в зависимость (5.26) в формуле для тока появляются в соответствии с (5.25) гармонические колебания с частотами W , w , 2W , 2w и с суммарной и разностной комбинационными частотами w + W и w – W .

Колебательный контур резонансного усилителя настроен на частоту w + W и выделяет из спектрального состава тока колебание

.

Выделенное колебание тока создает на резонансном сопротивлении контура падение напряжения

,

которое и является выходным сигналом преобразователя частоты.

В реальных системах связи передаваемый низкочастотный сигнал не является гармоническим, а имеет сложный спектр (рис. 5.49, а), т. е. состоит из суммы гармонических колебаний с частотами , , , ... .

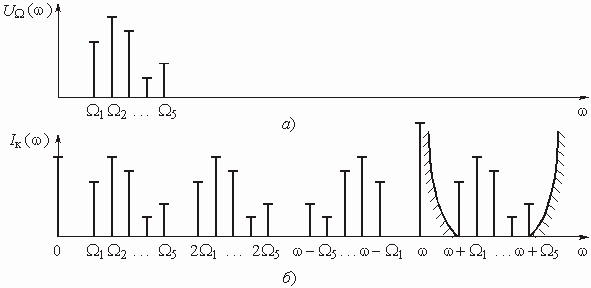
Рис. 5.49

Если этот сигнал вместе с высокочастотным колебанием подать на нелинейный элемент, то в спектре тока (рис. 5.49, б), протекающего через НЭ, будут присутствовать полезные продукты преобразования – комбинационные частоты , , , ... . Чтобы отфильтровать токи с этими частотами, недостаточно воспользоваться одиночным колебательным контуром, поскольку он не сможет обеспечить хорошую фильтрацию полезных продуктов преобразования. Его можно заменить в схеме рис. 5.48 обычной резистивной нагрузкой, а на выходе схемы включить электрический фильтр с характеристикой ослабления (на рис. 5.49, б она показана штриховой линией), обеспечивающей необходимую степень подавления несущего колебания с частотой w .

Приведем еще несколько практических схем преобразователей частоты. На рис. 5.50 представлены диодные преобразователи: однотактный (а), двухтактный или балансный (б) и кольцевой (в), работающие в режиме больших амплитуд колебания частоты w , т. е. в режиме аппроксимации ВАХ диодов линейно-ломаными функциями. Схема балансного транзисторного преобразователя частоты показана на рис. 5.51.

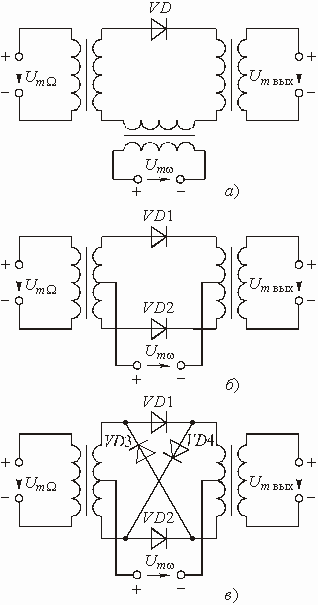
Рис. 5.50

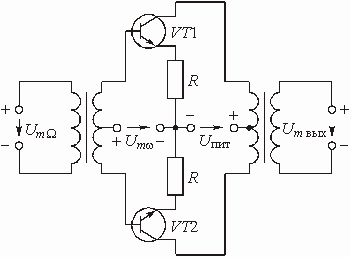
Рис. 5.51

В балансных и кольцевых преобразователях гораздо меньше побочных продуктов преобразования; тем самым значительно облегчаются требования к фильтру, выделяющему полезные колебания.

Вопросы и задания для самопроверки

1. Какие резистивные элементы называются нелинейными?

2. Определить статическое и динамическое сопротивления нелинейного элемента, имеющего ВАХ, изображенную на рис. 5.22.

Ответ: = 6 кОм; = 1,9 кОм.

3. Какие методы используют для расчета нелинейных цепей в режиме постоянного тока?

4. Рассчитать ток, протекающий через нелинейный элемент в схеме рис. 5.52, а, если заданы = 2 кОм, = 2 В, = 8 В, ВАХ НЭ приведена на рис. 5.52, б.

Ответ: = 2,7 мА.

5. Рассчитать ток I в схеме рис. 5.53, а, если R = 0,5 кОм, E = 2 В, ВАХ НЭ1 и НЭ2 приведены на рис. 5.53, б.

Ответ: I = 2,25 мА.

6. Каким образом формируются уравнения состояния нелинейных резистивных цепей?

7. Каков порядок расчета резистивных цепей с нелинейными четырехполюсниками?

8. Какие существуют виды аппроксимации ВАХ нелинейных элементов?

9. Аппроксимировать ВАХ НЭ, изображенную на рис. 5.8, в рабочем диапазоне 0 Ô Ô 1 В при = 0,5 В.

Ответ: .

10. Аппроксимировать ВАХ НЭ, изображенную на рис. 5.8, если к НЭ приложено напряжение .

Ответ:

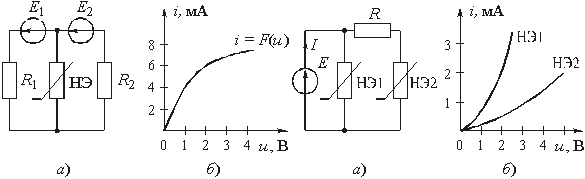
Рис. 5.52                                                    Рис. 5.53

11. Рассчитать амплитуды спектральных составляющих тока в задаче 9. Построить спектр тока.

Ответ: = 0,725 мА; = 0,75 мА; = 0,025 мА.

12. Рассчитать постоянную составляющую и амплитуды спектральных составляющих и тока в задаче 10. Построить спектр тока.

Ответ: q = 75,5°; = 0,6 мА; = 0,9 мА; = 0,5 мА.

13. Построить графики тока биполярного транзистора, ВАХ которого изображена на рис. 5.23, если заданы следующие значения :

а) ;

б) ;

в) .

14. По графикам рис. 5.35 и 5.37 пояснить принцип работы резистивного и резонансного нелинейных усилителей. Сравнить их КПД.

15. На вход резонансного усилителя (рис. 5.36) поступает гармоническое колебание частотой 50 кГц. Как получить на выходе напряжение частотой 150 кГц? Каким должен быть при этом угол отсечки и как добиться оптимального значения q?

16. Построить качественно графики напряжений в схемах ограничителей рис. 5.39, а – в.

17. По графику рис. 5.42 пояснить принцип работы выпрямителя, схема которого изображена на рис. 5.41.

18. Как сгладить пульсации напряжения на выходе выпрямителя?

19. Какой спектр имеет бигармоническое воздействие? Каков спектральный состав тока в цепи с НЭ, на который подано бигармоническое воздействие?

20. Какие комбинационные частоты будут в спектре НЭ, если его ВАХ аппроксимирована полиномом четвертой степени?

21. Каким образом можно перенести спектр сигнала по шкале частот?