1. При контакте двух полупроводников ![]() и
и ![]() –типа проводимости концентрация электронов и дырок по обе стороны от границы значительно различаются. Диффундируя во встречных направлениях через пограничный слой, дырки и электроны рекомбинируют. Поэтому область контакта оказывается сильно обедненной свободными носителями заряда и приобретает большое сопротивление. Кроме того, на границе оказывается двойной электрический слой, образованный отрицательными ионами акцепторной примеси и положительными ионами донорной примеси (на рисунке ионы примесей изображены кружками). Р – n – слой обеднен носителями зарядов из-за их взаимной компенсации. Этот слой создает электрическое поле
–типа проводимости концентрация электронов и дырок по обе стороны от границы значительно различаются. Диффундируя во встречных направлениях через пограничный слой, дырки и электроны рекомбинируют. Поэтому область контакта оказывается сильно обедненной свободными носителями заряда и приобретает большое сопротивление. Кроме того, на границе оказывается двойной электрический слой, образованный отрицательными ионами акцепторной примеси и положительными ионами донорной примеси (на рисунке ионы примесей изображены кружками). Р – n – слой обеднен носителями зарядов из-за их взаимной компенсации. Этот слой создает электрическое поле ![]() , противодействующее дальнейшему переходу через слой основных носителей.
, противодействующее дальнейшему переходу через слой основных носителей.
Возникшая контактная разность потенциалов равна:
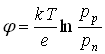 ,
,
где ![]() – концентрация дырок в материале
– концентрация дырок в материале ![]() –типа,
–типа, ![]() – концентрация дырок в материале
– концентрация дырок в материале ![]() –типа,
–типа, ![]() – постоянная Больцмана,
– постоянная Больцмана, ![]() – абсолютная температура,
– абсолютная температура, ![]() – заряд электрона.
– заряд электрона.
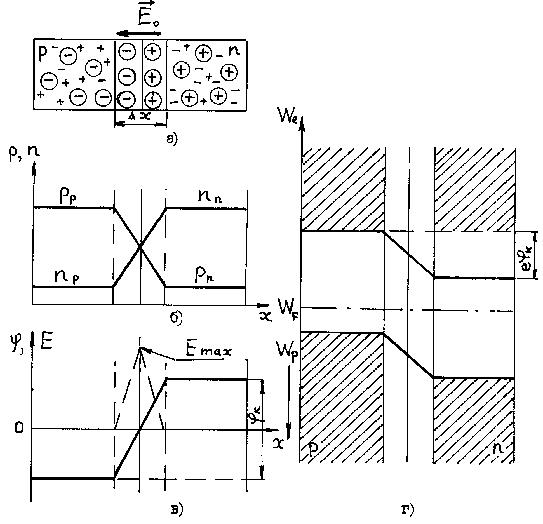
Рисунок 5.1 – ![]() –переход в равновесии
–переход в равновесии
а – схематическое изображение ![]() –перехода; б – распределение концентрации свободных носителей заряда вдоль оси Х; в – распределение потенциала вдоль оси Х; г – энергетическая диаграмма.
–перехода; б – распределение концентрации свободных носителей заряда вдоль оси Х; в – распределение потенциала вдоль оси Х; г – энергетическая диаграмма.
При ![]() К и
К и ![]() ,
, ![]() В. Ширина образовавшегося
В. Ширина образовавшегося ![]() –перехода равна:
–перехода равна:
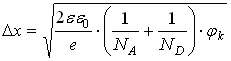
![]() и
и ![]() – концентрация акцепторов и доноров соответственно.
– концентрация акцепторов и доноров соответственно. ![]() мкм для предыдущего случая. Поле в
мкм для предыдущего случая. Поле в ![]() –переходе неоднородное. График распределения напряженности вдоль
–переходе неоднородное. График распределения напряженности вдоль ![]() –перехода представлен на рисунке 5.1в пунктиром, максимальная напряженность рассчитывается по формуле:
–перехода представлен на рисунке 5.1в пунктиром, максимальная напряженность рассчитывается по формуле:
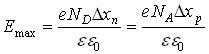 ,
,
где ![]() и
и ![]() – ширина положительной и отрицательной части
– ширина положительной и отрицательной части ![]() –перехода. При
–перехода. При ![]() – переход симметричный и
– переход симметричный и ![]() .
.
Для рассматриваемого выше численного примера:
![]() В/м .
В/м .
Равновесие достигается при такой высоте потенциального барьера ![]() , при которой значение энергии Ферми
, при которой значение энергии Ферми ![]() будет одинаково для всех областей (рисунок 5.1г). На рисунках изображены
будет одинаково для всех областей (рисунок 5.1г). На рисунках изображены ![]() –переход, распределение концентрации свободных носителей заряда (рисунок 5.1б) по областям, распределение потенциала (рисунок 5.1в) и энергетическая диаграмма
–переход, распределение концентрации свободных носителей заряда (рисунок 5.1б) по областям, распределение потенциала (рисунок 5.1в) и энергетическая диаграмма ![]() –перехода в равновесии (рисунок 5.1г). Собственное поле
–перехода в равновесии (рисунок 5.1г). Собственное поле ![]() –перехода препятствует диффузии через переход основных носителей (дырок из
–перехода препятствует диффузии через переход основных носителей (дырок из ![]() –области, электронов из
–области, электронов из ![]() –области) и ускоряет неосновные. В равновесии диффузионный ток основных носителей
–области) и ускоряет неосновные. В равновесии диффузионный ток основных носителей ![]() равен дрейфовому току неосновных
равен дрейфовому току неосновных ![]() . Полный ток
. Полный ток ![]() .
.
2. Если приложить к ![]() –переходу внешнее электрическое поле (
–переходу внешнее электрическое поле (![]() ) направление напряженности которого
) направление напряженности которого ![]() в области контакта противоположно собственному полю
в области контакта противоположно собственному полю ![]() (
(![]() ) (рисунок 5.2), то электроны от источника, поступая в
) (рисунок 5.2), то электроны от источника, поступая в ![]() –область уменьшают объемный заряд. Ширина
–область уменьшают объемный заряд. Ширина ![]() –перехода становится меньше:
–перехода становится меньше:
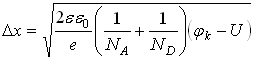 .
.
Меньше становится и скачок потенциала ![]() , т. е. барьер для основных носителей заряда уменьшится и через переход идет диффузионный ток, плотность которого возрастает с увеличением приложенного напряжения по экспоненциальному закону:
, т. е. барьер для основных носителей заряда уменьшится и через переход идет диффузионный ток, плотность которого возрастает с увеличением приложенного напряжения по экспоненциальному закону:
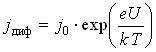 .
.
Дрейфовый ток определяется только числом неосновных носителей ![]() . Плотность полного тока через
. Плотность полного тока через ![]() –переход называемого в этом случае прямым, равна:
–переход называемого в этом случае прямым, равна:
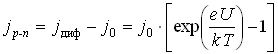 .
.
Следовательно при прямом включении через p–n–переход вводится (инжектируется) дополнительная концентрация неосновных носителей заряда (дырок в n–область и электронов в p–область). Распределение концентрации свободных носителей при прямом включении представлена сплошной кривой на рисунке 5.2б. По мере удаления от ![]() –перехода концентрация инжектированных неосновных носителей заряда убывает за счет рекомбинации до равновесной. Небольшое возрастание концентрации основных носителей заряда около
–перехода концентрация инжектированных неосновных носителей заряда убывает за счет рекомбинации до равновесной. Небольшое возрастание концентрации основных носителей заряда около ![]() –перехода наблюдается только при больших уровнях инжекции за счет “притягивания” основных носителей инжектированными неосновными. Инжекция является одним из важных способов введения неравновесной концентрации зарядов.
–перехода наблюдается только при больших уровнях инжекции за счет “притягивания” основных носителей инжектированными неосновными. Инжекция является одним из важных способов введения неравновесной концентрации зарядов.
3. Если внешнее поле ![]() совпадает по направлению с собственным полем
совпадает по направлению с собственным полем ![]() –перехода, то
–перехода, то ![]() , контактная разность потенциалов возрастает
, контактная разность потенциалов возрастает ![]() , переход станет шире:
, переход станет шире:
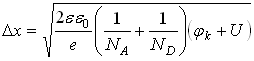 .
.
Поле p–n–перехода становится “более ускоряющим” для неосновных носителей и удаляет часть этих носителей из объема вблизи ![]() –перехода. Этот процесс называется экстракцией. В результате экстракции неосновных носителей заряда электрическим полем (на рисунке 5.3 представлено распределение свободных носителей заряда), концентрация неосновных носителей вблизи p–n–перехода уменьшается. Энергетический барьер для диффузии основных носителей заряда увеличится и диффузионный ток быстро уменьшится до нуля. Полный ток при этом определится дрейфовым током неосновных носителей заряда. Этот ток очень мал и называется обратным током. Следовательно, переход обладает способностью проводить ток в одном направлении значительно больше, чем в другом. Зависимость плотности тока через идеальный
–перехода. Этот процесс называется экстракцией. В результате экстракции неосновных носителей заряда электрическим полем (на рисунке 5.3 представлено распределение свободных носителей заряда), концентрация неосновных носителей вблизи p–n–перехода уменьшается. Энергетический барьер для диффузии основных носителей заряда увеличится и диффузионный ток быстро уменьшится до нуля. Полный ток при этом определится дрейфовым током неосновных носителей заряда. Этот ток очень мал и называется обратным током. Следовательно, переход обладает способностью проводить ток в одном направлении значительно больше, чем в другом. Зависимость плотности тока через идеальный ![]() –переход от внешнего напряжения представлена на рисунке 5.4 и определяется следующей формулой:
–переход от внешнего напряжения представлена на рисунке 5.4 и определяется следующей формулой:
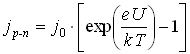 ,
,
где ![]() – плотность обратного тока при достаточно большом напряжении.
– плотность обратного тока при достаточно большом напряжении.
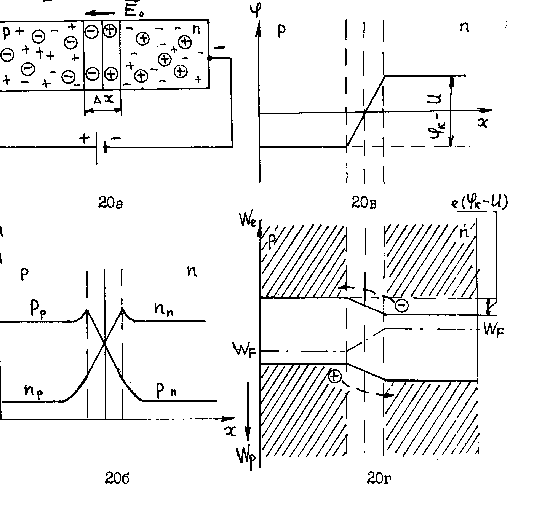
Рисунок 5.2 – ![]() –переход при прямом включении
–переход при прямом включении
а – схематическое изображение ![]() –перехода; б – распределение свободных носителей; в – распределение потенциала; г – энергетическая диаграмма.
–перехода; б – распределение свободных носителей; в – распределение потенциала; г – энергетическая диаграмма.
Для расчета прямого тока ![]() подставляется со знаком (+), а для обратного со знаком (-). Значение
подставляется со знаком (+), а для обратного со знаком (-). Значение ![]() (плотность тока насыщения), созданного неосновными электронами и дырками может быть вычислена по формулам:
(плотность тока насыщения), созданного неосновными электронами и дырками может быть вычислена по формулам:
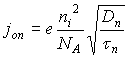 ,
,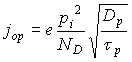 ,
,
где ![]() ,
, ![]() – среднее время жизни электрона и дырки соответственно
– среднее время жизни электрона и дырки соответственно ![]() ,
, ![]() – коэффициенты диффузии, вычисленные по формулам Эйнштейна:
– коэффициенты диффузии, вычисленные по формулам Эйнштейна:
![]() ,
,
![]()
![]() и
и ![]() – подвижности электронов и дырок соответственно.
– подвижности электронов и дырок соответственно.
Суммарная плотность тока j0 через p–n– переход равна:
![]()
На рисунке 5.4 отражено влияние температуры на зависимость j от ![]() на примере германия. При увеличении температуры
на примере германия. При увеличении температуры ![]() –перехода возрастает термогенерация электронно–дырочных пар, что значительно сказывается на величине обратного тока, определяемого малым количеством неосновных носителей (пунктирная кривая рисунка 5.4) На рисунке 5.5 показаны в сравнении зависимости j от
–перехода возрастает термогенерация электронно–дырочных пар, что значительно сказывается на величине обратного тока, определяемого малым количеством неосновных носителей (пунктирная кривая рисунка 5.4) На рисунке 5.5 показаны в сравнении зависимости j от ![]() для идеального
для идеального ![]() –перехода (сплошная кривая) и реального. Отличие в прямой ветви характеристики объясняется падением напряжения на “объеме” полупроводников
–перехода (сплошная кривая) и реального. Отличие в прямой ветви характеристики объясняется падением напряжения на “объеме” полупроводников ![]() и
и ![]() –типа, в обратной ветви – током утечки по поверхности и наступающим при определенном
–типа, в обратной ветви – током утечки по поверхности и наступающим при определенном ![]() пробое (электрическом, тепловом).
пробое (электрическом, тепловом).
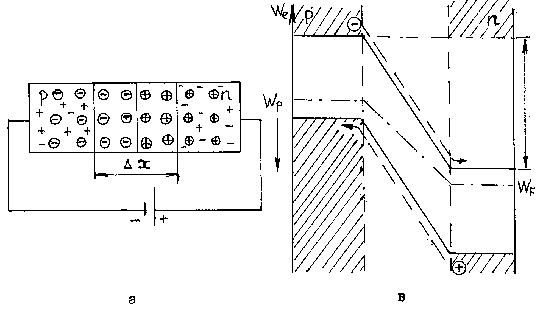
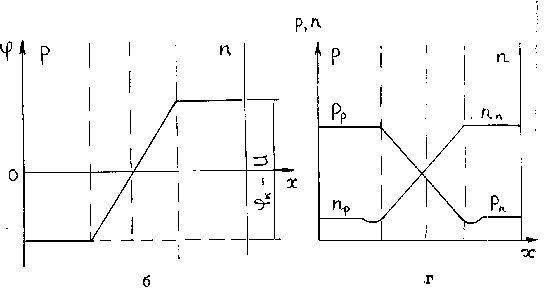
Рисунок 5.3 – ![]() –переход при обратном включении
–переход при обратном включении
а – схематическое изображение ![]() –перехода; б – распределение потенциала вдоль оси Х; в – энергетическая диаграмма; г – распределение концентрации свободных носителей заряда.
–перехода; б – распределение потенциала вдоль оси Х; в – энергетическая диаграмма; г – распределение концентрации свободных носителей заряда.
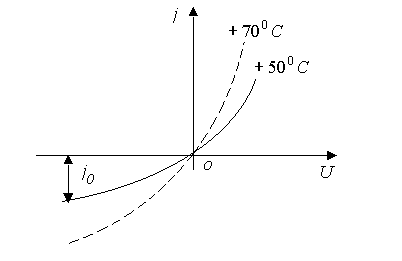
Рисунок 5.4 – Зависимость тока через ![]() –переход от напряжения при разных температурах
–переход от напряжения при разных температурах
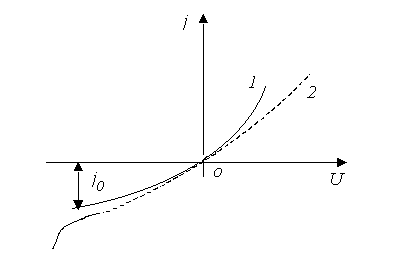
Рисунок 5.5 – Зависимость тока через ![]() –переход от напряжения
–переход от напряжения
1 – идеальный ![]() –переход; 2 – реальный
–переход; 2 – реальный ![]() –переход.
–переход.

