Дискретный сигнал и его спектр описываются формулами (8) и (7).

Произведем в формуле (7) замену:

.

Тогда формула примет вид:

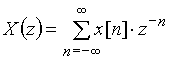. (12)

Выражение (12) получило название z-преобразования или z-изображения дискретного сигнала . Если начать суммирование с n = 0, то выражение

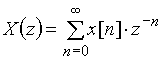. (13)

есть одностороннее z-преобразование. Оно применяется для сигналов º 0 при n < 0.

Можно указать на связь z-преобразования с преобразование Лапласа дискретного сигнала

,

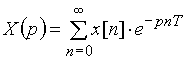которое легко получить из (7), положив .

Очевидно, что или .

Эти формулы устанавливают связь между точками в плоскостях и (рис. 20).

Если положить a = 0, то мы будем перемещаться по оси jw в плоскости р. При переходе в z-плоскость точки мнимой оси jw будут располагаться на единичной окружности . Причем, точка j0 на р-плоскости переходит в точку z = +1 на вещественной оси z-плоскости, а точки – в точку z = –1. Это означает, что точки отрезка () р-плоскости проектируются в точки на единичной окружности z-плоскости. Так как функция периодическая, то последующие отрезки оси jw на p-плоскости такой же длины будут вновь проектироваться на единичную окружность.

Точкам левой р-полуплоскости соответствуют точки внутри единичной окружности z-плоскости, а точкам правой p-полу­плос­кости – точки вне этой окружности.

Пример 9.1. Рассчитаем z-преобразование дискретного сигнала , имеющего вид

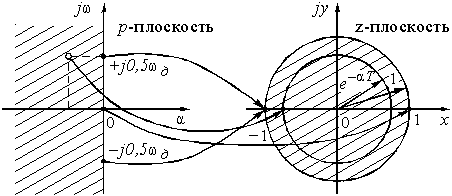
Рис. 20

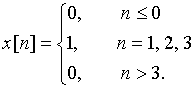
Воспользовавшись формулой (13), получим

.

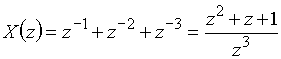Пример 9.2. Найдем z-преобразование дискретного экспоненциального сигнала.

Подставим значение в формулу (13), получим

.

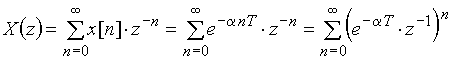Из теории рядов следует, что при выполнении условия сумма ряда равна 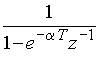или .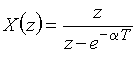

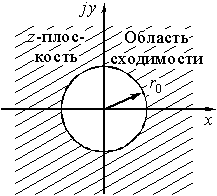
Рис. 21

Z-преобразование дискретного сигнала определено толь­ко для области z, в которой степенной ряд (13) сходится. Эта область сходимости включает в себя все значения z, находящиеся вне некоторого круга на комплексной z-плоскости, радиус которого называется радиусом сходимости (рис. 21), т.е. при ряд сходится. В области сходимости существует взаимно-однозначное соответствие между и , т.е. каждому соответствует одно и только одно , определенное для и наоборот.

Пример 9.3. Определим радиус сходимости для z-преобра­зо­ва­­ния сигнала, заданного в примере 9.2.

Как уже было установлено, z-преобразование сигнала имеет вид

.

Нуль функции будет в точке , полюс – в точке . Следовательно, радиус сходимости , а функция сходится при .

Окружность, имеющая радиус сходимости , приведенана рис. 20. Область сходимости находится за пределами этой окружности.

Пример 9.4. Найдем z-преобразование сигнала , n ³ 0. Этот дискретный сигнал показан на рис. 22 для трех различных значений a: а = 0,8; а = 1; а = –0,8.

В соответствии с (13) z-преобразование такого дискретного сигнала равно

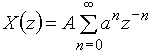. (14)

Из математики известно, что этот ряд сходится к функции

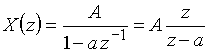, (15)

если или .

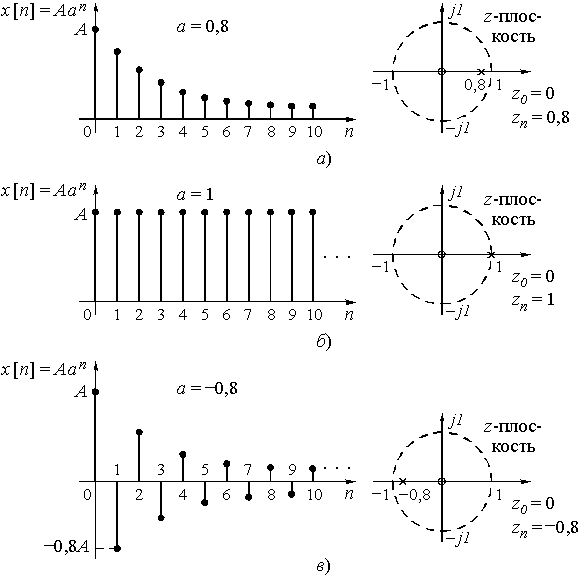
Рис. 22

Функция имеет нуль при z = 0, а ее полюс лежит на окружности радиусом , ограничивающей область сходимости.

На рис. 22 показано расположение нуля и полюса функции в z-плоскости при различных а.

Самоконтроль

1. Как рассчитать z-изображение дискретного сигнала?

2. Как связаны одностороннее z-преобразование и преобразование Лапласа?

3. Какие точки z-плоскости соответствуют точкам левой (правой) р-полуплоскости?

4. Что такое радиус сходимости?

5. Найдите z-изображение дискретного сигнала = {0; 1; 2; 3}.

6. Найдите z-изображение дискретного сигнала .

7. Найдите радиус сходимости для z-преобразования сигнала .