7.2. Равномерное квантование мгновенных значений сигнала
7.3. Неравномерное квантование мгновенных значений
7.6. Теория разностного кодирования
7.8. Адаптивно-разностная ИКМ (АРИКМ)
7.1. Вводные замечания
Методы рационального кодирования предназначены для сокращения избыточности сообщений в условиях априорной неопределенности относительно статистических характеристик сигналов [4]. Т.е. в условиях, когда сигнал является нестационарным, что часто встречается на практике, или когда неизвестны статистические характеристики этого сигнала. Под рациональным кодированием понимают такое кодирование, при котором измерительная информация представленная в дискретной форме требует минимальное количество символов при заданной верности, т.е. отношении сигнал – шум квантования. Требование рационального кодирования сообщений обусловлены тем, обстоятельством, что в случае нерационального кодирования на первом этапе избыточность сохраняется и на последнем. В случае применения корректирующих (помехоустойчивых) кодов избыточность сообщений еще более возрастает. Процедуры рационального кодирования источника сообщений классифицируются по их возможности менять параметры или структуру кодирующего устройства для обеспечения сжатия данных. Классификация имеет вид (рисунок 7.1).
Рисунок 7.1
Фиксированная процедура имеет заданную структуру, которая остается неизменной при любых входных воздействиях. Это не позволяет оптимизировать процесс обработки данных при разных сообщениях на входах квантователя (можно оптимизировать для класса разных сообщений), но допускает простую аппаратную реализацию алгоритма. Пример фиксированной процедуры - 
-квантователь.
Параметрическая адаптивная процедура чувствительна к статистике сообщений и изменяется в соответствии с выбранным критерием свои параметры. Примерами такой процедуры являются адаптивная и разностная ИКМ.
Непараметрическая адаптивная процедура сжатия данных с изменением структуры алгоритмов сообщений является наиболее перспективной с точки зрения эффективности кодирования источника нестационарных сообщений с изменяющимися статистическими характеристиками. В этом случае меняются не только параметры, но и структура алгоритма кодирования. К таким процедурам относят алгоритм адаптивно - разностной ИКМ с перестройкой структуры фильтра – предсказателя.
7.2. Равномерное квантование мгновенных значений сигнала
Предположим, что в результате дискретизации сигнала получается последовательность непрерывных величин 
для передачи по цифровым каналам связи. Каждый отсчет необходимо проквантовать до конечного множества значений. Целесообразно разделять процесс представления последовательности множеством двоичных символов на два этапа: квантование, результатом которого является последовательность величин 
=
и кодирование, когда последовательности величин ставится в соответствие кодовое слово 
, т.е. этот процесс можно представить в виде (рисунок 7.2).
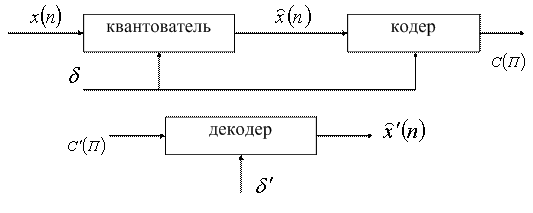
Рисунок 7.2
Обычно для кодирования квантованных отсчетов используют двоичную последовательность. С помощью B-разрядного кодового слова можно представить 
уровней квантования. Скорость передачи информации в этом случае:
, (7.1)
где 
- частота дискретизации, которая выбирается исходя из способа восстановления сигнала в приемнике, 
- число бит на отсчет сигнала.
Если - const, то единственный путь уменьшения скорости передачи состоит в сокращении числа двоичных единиц на отсчет сигнала. Определим как зависит отношение сигнал – шум квантования от разрядности кодового слова .
Рассмотрим различные способы квантования сигнала. Пусть
(7.2)
и функция плотности вероятности сигнала симметрична. Тогда
. (7.3)
Для речевого сигнала с функцией плотности вероятностей (ФПВ) Лапласа только 0,55% отсчетов сигнала окажутся вне динамического диапазона:
. (7.4)
В случае равномерного квантования:
. (7.5)
Рассмотрим характеристики равномерного квантователя в случае восьми уровневого квантования.
Первый случай. Квантователь с усечением (рисунок 7.3) имеет одинаковое количество положительных и отрицательных уровней, но нет нулевого.
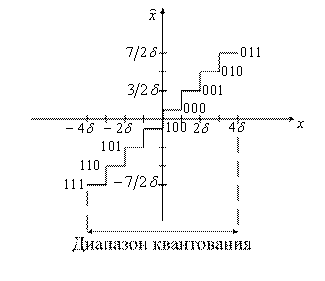
Рисунок 7.3
Второй случай. Квантователь с округлением (рисунок 7.4) имеет на один отрицательный уровень больше, но есть нулевой уровень.
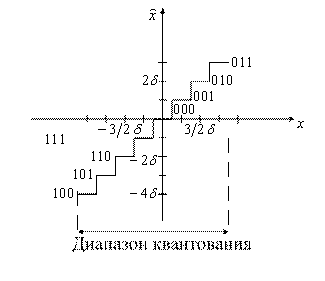
Рисунок 7.4
Для квантователя с усечением при предположении, что первый разряд знаковый, квантованное значение равно:
, (7.6)
а для квантователя с округлением:
. (7.7)
. (7.8)
Представим квантованный сигнал в виде :
(7.9)
где 
- ошибка или шум квантования, 
.
Для изучения эффектов квантования предполагают, что шум квантования обладает следующими статистическими свойствами:
- Является стационарным белым шумом.
- Некоррелирован со входным сигналом.
- Распределение шума равномерное в пределах
.
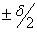Для этой статистической модели определим отношение сигнал – шум квантования:
, (7.10)
где M – оператор усреднения.
Для B-разрядного квантователя можно записать соотношения:
. (7.11)
Тогда дисперсия шумов квантования 
при равномерном распределении ошибки равна:
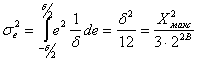. (7.12)
В случае, если 
, то получим выражение для отношения сигнал – шум квантования:
. (7.13)
Обычно отношение сигнал – шум задается в дБ:
. (7.14)
Из выражения (7.14) следует, что добавление одного разряда кодового слова улучшает отношение сигнал – шум квантования на 6 дБ. Выражение для отношения сигнал – шум квантования получено при предположении, что диапазон квантования используется полностью, если энергия сигнала изменится, то отношение сигнал – шум квантования уменьшится. В реальных условиях дисперсия телеметрического сигнала можно меняться на 20-30дБ. По этой причине для поддержания отношения сигнал – шум квантования на заданном уровне в случае равномерного квантования необходимо увеличивать число уровней квантования, при этом увеличивается избыточность сообщения. Желательно иметь устройство квантования, при котором отношение сигнал – шум квантования не зависит от уровня сигнала. Это достигается использованием неравномерного распределения уровней квантования.
7.3. Неравномерное квантование мгновенных значений
Для того чтобы относительная ошибка была постоянна при изменении дисперсии входного сигнала уровни квантования должны быть распределены по логарифмическому закону. Вместо квантования исходного сигнала можно равномерно квантовать его логарифм. В этом случае структурная схема квантователя имеет вид (рисунок 7.5).
Докажем, что в случае 
отношение сигнал – шум квантования не зависит от изменения дисперсии входного сигнала.
Выражение для квантованного логарифма входного сигнала имеет вид:
. (7.15)
Предполагается, что шумы квантования и 
независимы.
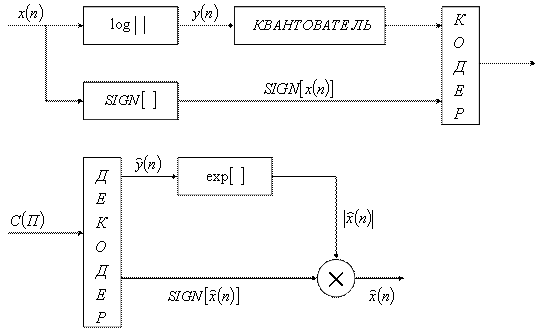
Рисунок 7.5
Тогда применяя обратное преобразование, получим:
. (7.16)
Если значение ошибки 
мало, то можно аппроксимировать экспоненту первыми членами ряда, т.е.:
(7.17)
При условии, что 
и 
независимы 
и отношение сигнал – шум равно:
. (7.18)
Следовательно, отношение сигнал - шум квантователя не зависит от мощности сигнала и зависит только от шага квантования.
Рассмотренный выше квантователь не реализуем, т.к. динамический диапазон сигнала бесконечен и требует бесконечное число уровней квантования. Для реальных случаев число уровней квантования конечно, и характеристика компрессора может быть близка к логарифмической. На практике используемые характеристики компрессора называются и А законами компандирования.
- закон компандирования имеет следующий вид:
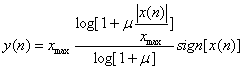. (7.19)
При малых 
и уровни квантования располагаются равномерно. При больших :
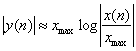(7.20)
и эта характеристика близка к логарифмической.
Можно показать, что чем выше значение параметра , тем ближе характеристика компандирования к логарифмической, но тем больше проигрыш в отношении сигнал/шум. Если дисперсия входного сигнала постоянна и известна, то неравномерный квантователь проигрывает равномерному. Экспериментальные исследования показали, что двенадцатиразрядное равномерное квантование имеет такое же отношение сигнал/шум, как и в случае восьмиразрядного квантования при - законе компандирования в случае речевого сигнала (рисунок 7.6).
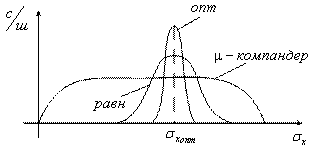
Рисунок 7.6
При 
. Отношение сигнал-шум квантования для - закона компандирования равно
(7.21)
А - закон компандирования имеет вид:
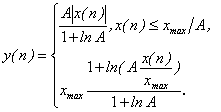(7.22)
7.4. Оптимальное квантование
Как было установлено, квантование по - закону позволяет получить постоянное отношение сигнал-шум квантователя в широком диапазоне дисперсий входного сигнала. Это достигается ценой некоторого уменьшения отношения сигнал-шум квантователя по сравнению со случаем, если диапазон квантования согласован с дисперсией входного сигнала. Когда дисперсия сигнала известна, можно так выбрать уровени и пороги квантования, чтобы минимизировать мощность шума, т.е. максимизировать отношение сигнал-шум квантователя
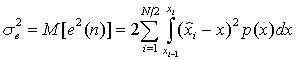, (7.23)
- ФПВ сигнала. Выражение (7.23) написано при симметричной функции плотности вероятности сигнала.
Требуется выбрать множество таких порогов и уровней квантования, чтобы минимизировать дисперсию входного сигнала. Для решения этой задачи продифференцируем 
по этим параметрам и приравняем производную к нулю
, 
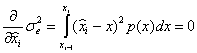(7.24)
(7.25)
При условии, что 
, 
из выражения (7.24) и (7.25) следует, что
, (7.26)
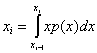. (7.27)
Т.е. оптимальные пороги равны полусумме уровней квантования, а уровни квантования есть среднее значение ФПВ сигнала на интервале 
.
Данное уравнение решается с помощью итерактивных методов для заданной ФПВ сигнала. Решение уравнения приводит к неравномерному распределению уровней квантования. Равномерное распределение уровней квантования будет только для сигналов с равномерной ФПВ. Оптимальные размеры шага квантования определены для нормального распределения, 
- распределения и распределения Лапласа.
Оптимальный квантователь дает минимум погрешности, если известна дисперсия и форма ФПВ сигнала.
Реальные сигналы обычно нестационарны. Поэтому на практике чаще используются - квантователи, несмотря на несколько меньшее отношение сигнал-шум квантователя по сравнению с оптимальными. Обычно потери составляют 3 – 6 дБ, т.е. меньше, чем один разряд квантования при известной дисперсии входного сигнала.
7.5. Адаптивное квантование
7.5.1. Вводные замечания
Из п. 7.4 ясно, что шаг квантования 
необходимо выбирать большим для согласования диапазона квантования с размахом сигнала. С другой стороны необходимо выбирать малым для уменьшения шума квантования. Одним из путей решения этой проблемы при нестационарном входном сигнале является применение - компандирования. Другой путь состоит в адаптации квантования к уровню входного сигнала. Если адаптивное квантование применяется непосредственно к отсчетам входного сигнала, то такой метод обработки называют адаптивной ИКМ (АИКМ). Известны два способа реализации АИКМ. Адаптивное квантование при первом способе состоит в том, что шаг квантования (в общем случае интервалы и уровни квантования) изменяются таким образом, чтобы соответственно изменялась дисперсия входного сигнала.
Другой способ реализации АИКМ соответствует случаю, когда характеристики квантователя не изменяются, а постоянный уровень дисперсии сигнала поддерживается за счет переменного коэффициента усиления. В обоих случаях необходимо оценивать изменяющиеся во времени характеристики сигнала.
Имеется два класса схем адаптивного квантования:
- Квантователь с адаптацией по входу, когда дисперсия входного сигнала оценивается непосредственно по этому сигналу.
- Квантователь с адаптацией по выходу, когда шаг квантования подстраивают по выходному сигналу
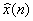или кодовому слову 
.
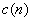7.5.2. Адаптация по входному сигналу
Рассмотрим структурную схему квантователя с переменным шагом квантования (рисунок 7.7).
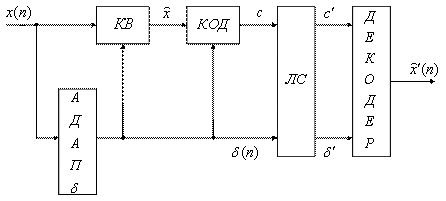
Рисунок 7.7
Шаг квантования должен быть известен на приемной стороне, т.е. в этом случае отсчет описывается кодовым словом и шагом квантования. Если используется квантователь с адаптацией по входу на основе усилителя с переменным коэффициентом усиления, то квантованный сигнал описывается кодовым словом и коэффициентом усиления.
Структурная схема квантователя с переменным коэффициентом квантования приведена на следующем рисунке (рисунок 7.8).
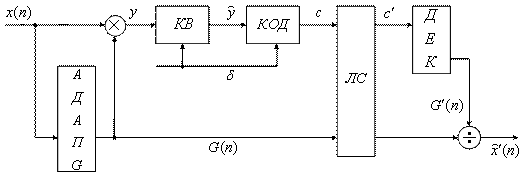
Рисунок 7.8
В системах адаптации по шагу и усилению обычно используется оценка дисперсии входного сигнала. В этом случае шаг или уровни квантования устанавливаются пропорционально СКО сигнала
, (7.28)
а коэффициент усиления - обратно пропорционально
. (7.29)
Общий подход состоит в предположении, что дисперсия входного сигнала пропорциональна кратковременной энергии. При этом дисперсия входного сигнала оценивается по формуле:
(7.30)
- импульсная характеристика фильтра нижних частот.
В интересах практической реализации устройств адаптации импульсная характеристика фильтра выбирается в виде:
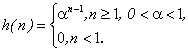(7.31)
Тогда дисперсия входного сигнала равна:
, (7.32)
(7.33)
Параметр 
импульсной характеристики фильтра определяет протяженность интервала времени, на котором сигнал вносит основной вклад в оценку дисперсии.
Обе схемы адаптивных квантователей по входу сигнала идентичны с точки зрения отношения сигнал-шум квантователя. Экспериментальные исследования в случае, если сигнал имеет ФПВ Гаусса или Лапласа показали, что адаптивное квантование дает выигрыш в отношении сигнал-шум квантователя не менее 5 - 6 дБ по сравнению с - квантователем. Если дисперсия входного сигнала изменяется в широких пределах (30 дБ и более), этот выигрыш будет увеличиваться.
7.5.3. Адаптация по выходному сигналу
Схема адаптации по выходу с переменным шагом квантования имеет вид (рисунок 7.9).
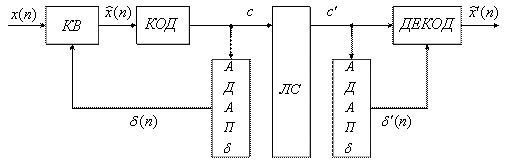
Рисунок 7.9
Системы адаптации по шагу в этой схеме цифровые. Схема адаптации по выходу с переменным коэффициентом усиления имеет вид (рисунок 7.10).
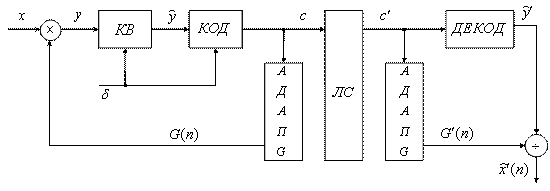
Рисунок 7.10
В обеих схемах дисперсия входного сигнала оценивается по выходному квантованному сигналу или по последовательности кодовых слов. Такие схемы обладают важным преимуществом по сравнению со схемами адаптации по входному сигналу, состоящие в том, что шаг квантования или коэффициент усиления не требуется сохранять или передавать по КС. Кроме того, система адаптации может быть реализована в цифровом виде.
Недостатком подобных квантователей является высокая чувствительность к ошибкам в кодовых словах, т.к. эти ошибки приводят не только к неправильной установке уровней квантования, но и ошибкам в шаге квантования.
Дисперсия входного сигнала в этом случае рассчитывается по формуле:
, (7.34)
где 
- квантованное значение входного сигнала, а импульсная характеристика равна:
(7.35)
При оценке дисперсии в схемах адаптации по входу вместо используют .
Исследования схем адаптации по выходному сигналу показали, что по сравнению с - квантователем достигается выигрыш не менее 5 дБ.
Методы адаптивного квантования дают выигрыш в отношении сигнал-шум квантователя по сравнению с квантованием по - закону при том же динамическом диапазоне сигнала. Этот выигрыш зависит от формы ФПВ входного сигнала и его динамического диапазона. В связи с этим представляет интерес рассмотрение методов разностного кодирования, которые менее чувствительны к форме ФПВ входного сигнала.
7.6. Теория разностного кодирования
Обычно между соседними отсчетами входного сигнала имеется значительная корреляция, которая слабо уменьшается по мере увеличения интервала между отсчетами. В результате разность между соседними отсчетами имеет меньшую дисперсию, чем исходный сигнал. Т.е. динамический диапазон разностного квантованного сигнала уменьшается, что позволяет при том же отношении сигнал – шум квантования уменьшить разрядность кодового слова (рисунок 7.11).
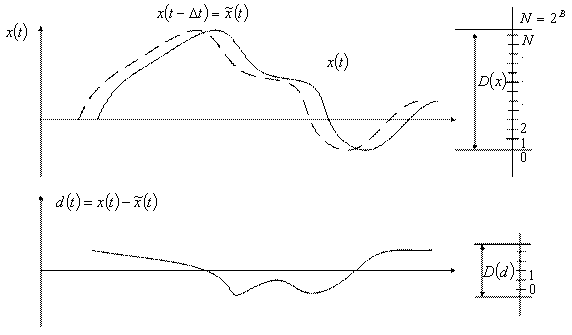
Рисунок 7.11
Рассмотрим два случая:
1. 
, т.е. кодовое слово разностного сигнала уменьшится.
2. 
. Т.е. динамический диапазон разностного сигнала расширяется до динамического диапазона исходного сигнала. Тогда длительность кодового слова исходного и разностного сигналов равны, а отношение сигнал – шум квантования разностного сигнала 
.
Рассмотрим особенности работы разностного квантователя (рисунок 7.12).
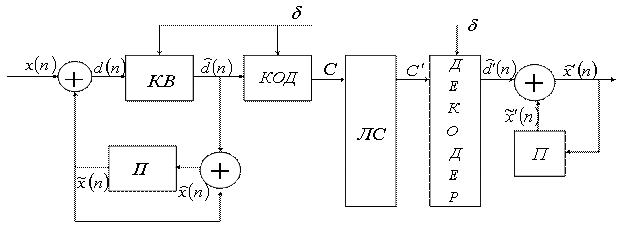
Рисунок 7.12
На входе квантователя (КВ) действует сигнал:
. (7.36)
Сигнал 
называется погрешностью предсказания или разностный сигнал. Квантованию подвергается не входной, а разностный сигнал. Квантователь может быть адаптивным или неадаптивным, равномерным или неравномерным, но во всех случаях его параметры соответствуют дисперсии погрешности предсказания. Квантованная погрешность предсказания имеет вид:
, (7.37)
где 
- ошибка квантования разностного сигнала. Из структурной схемы (7.12) следует, что квантованное значение исходного сигнала имеет вид:
. (7.38)
Тогда используя формулы (7.36 – 7.38) получаем выражение:
(7.39)
. (7.40)
Таким образом квантованный входной сигнал отличается от исходного входного сигнала на величину шума квантования разностного сигнала. Если предсказатель (П) хороший, то дисперсия разностного сигнала будет меньше дисперсии входного сигнала и квантователь с заданным количеством уровней даст меньшую погрешность при квантовании разности, чем при квантовании исходного сигнала. Отношение сигнал – шум квантования в этом случае имеет вид:
, (7.41)
где 
- отношение сигнал – шум квантователя, 
- коэффициент усиления, обусловленный разностным кодированием. Отношение сигнал – шум квантователя зависит только от свойств квантователя (равномерный, неравномерный, адаптивный) и разностного сигнала. Величина определяет выигрыш в отношении сигнал – шум при использовании разностного представления. Т.к. величина 
фиксированная, то увеличить коэффициент усиления можно только за счет минимизации 
. Для решения этой задачи определяют тип предсказателя. Рассмотрим возможность использования линейного предсказателя:
, (7.42)
где 
- порядок фильтра предсказателя, 
- коэффициенты. Дисперсия погрешности предсказателя в этом случае имеет вид:
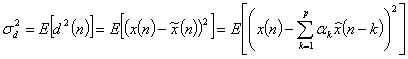. (7.43)
Дифференцируя по и приравниваем к нулю, получим систему уравнений:
(7.44)
Решением системы уравнений будут коэффициенты , при которых минимальна. В этом случае коэффициент усиления равен:
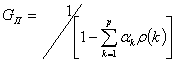, (7.45)
где 
- нормированная корреляционная функция 
. Таким образом пока 
отношение сигнал – шум квантования будет увеличиваться за счет предсказания. В случае речевого сигнала при 
получаются зависимости коэффициента усиления 
от порядка фильтра предсказателя (рисунок 7.13)
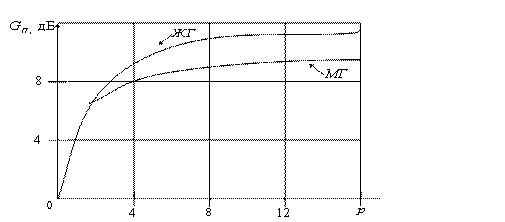
Рисунок 7.13
Даже при простом предсказателе, когда p=1, можно получить выигрыш в 6 дБ по сравнению с ИКМ, что эквивалентно добавления одного разряда в квантователь. В случае женского голоса (ЖГ) выигрыш разностного квантования выше, чем в случае мужского голоса (МГ).
Выводы:
- Разностное квантование обеспечивает выигрыш по сравнению с неадаптивным квантователем в (6 – 12) дБ.
- Величина выигрыша зависит от величины корреляции между отсчетами.
- Один и тот же предсказатель не может быть оптимальным для различных сигналов, т.к. значения коэффициентов 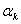зависят от вида корреляционной функции сигнала.
7.7. Дельта – модуляция
7.7.1. Общие замечания
При дельта – модуляции частота дискретизации много выше, чем частота В.А.Котельникова, 
. В результате соседние отсчеты оказываются сильно коррелированными, т.е.:
(7.46)
и можно более точно предсказать текущий отсчет по предшествующему. Т.к. в системе с дельта – модуляцией используется одноразрядный (двухуровневый) квантователь, то скорость передачи информации при этом равняется частоте дискретизации 
.
7.7.2. Линейная дельта – модуляция
В этом случае шаг квантования фиксирован, а порядок фильтра - предсказателя p=1. Квантователь имеет два уровня:
(7.47)
Коэффициент усиления при этом:
. (7.48)
При 
, коэффициент усиления 
, но этот результат качественный, практически же коэффициент усиления стремится к постоянному предельному значению 
.
Структурная схема системы с дельта – модуляцией имеет вид (рисунок 7.14).
Рисунок 7.14
Приемная часть схемы изображена на рисунке 7.15.
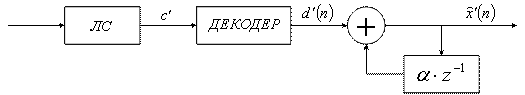
Рисунок 7.15
Рассмотрим сигналы в различных точках этой схемы (рисунок 7.16).
При дельта – модуляции в тактовых точках передается знак приращения текущего значения сигнала относительно предшествующего. При увеличении исходного сигнала формируется последовательность единиц, а при уменьшении – последовательность нулей. Квантованное значение в этом случае имеет вид:
. (7.49)
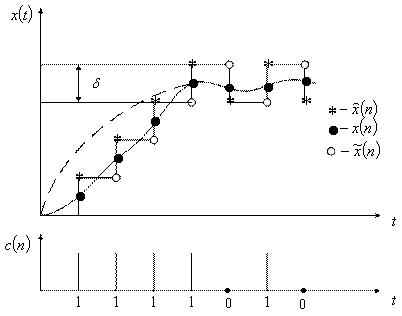
Рисунок 7.16
При 
это уравнение описывает работу дискретного интегратора, в котором осуществляется накопление шагов квантования 
.
Рассмотрим требования к характеристикам дельта – модулятора. Входной сигнал квантователя имеет вид:
, (7.50)
где - ошибка квантования.
Если пренебречь ошибкой квантования, то рассматривается как аппрокимация производной входного сигнала. Для того, чтобы последовательность отсчетов 
быстро возрастала как и последовательность отсчетов необходимо потребовать выполнение условия:
. (7.51)
Если это условие не удовлетворяется, то возникает ошибка перегрузки (пунктирная кривая на рисунке 7.16). Т.к. при перегрузке увеличение и уменьшение последовательности происходит по ступенчатой линии, то такую дельта – модуляцию называют линейной (ЛДМ).
Если в течение некоторого интервала времени входной сигнал меняется незначительно, то в линию связи поступает последовательность нулевых и единичных посылок, что приводит к флюктуациям восстановленного сигнала с размахом 
дельта, возникает шум дробления.
Рассмотрим вопрос выбора оптимального шага квантования. При большом динамическом диапазоне входного сигнала необходимо выбирать большой шаг квантования. Для точного описания малых уровней входного сигнала необходим меньший шаг квантования. Выбор шага квантования необходимо производить с условием максимизации отношения сигнал – шум квантования при заданной частоте дискретизации. Эти зависимости были исследованы для сигнала с гауссовской ФПВ и равномерным спектром. Они имеют вид (рисунок 7.17).
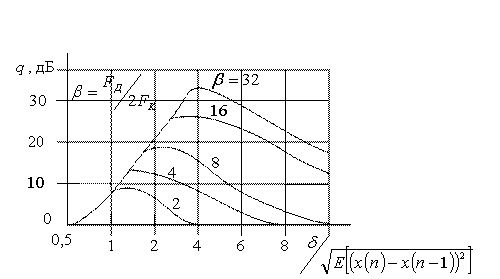
Рисунок 7.17
При некотором 
отношение сигнал – шум квантования достигает максимума. Значения левее 
соответствует перегрузке, а правее - 
- шуму дробления. Оптимальное значение отношения сигнал – шум квантования увеличивается на 9 дБ при удвоении 
, что увеличивает скорость передачи в 2 раза.
Достоинства линейной дельта – модуляции:
- Простая реализация.
- Низкие требования к синхронизации.
Недостаток линейной дельта – модуляции: грубое квантование погрешности предсказания.
7.7.3. Адаптивная дельта - модуляция
Адаптивные схемы дельта - модуляторов (АДМ) позволяют значительно улучшить характеристики ЛДМ, в частности грубое квантование погрешности предсказания. Обычно при АДМ используется адаптация по выходному сигналу. В этом случае не требуется синхронизация по кодовым словам, т.к. шаг квантования в передатчике и приемнике перестраивается в одной и той же кодовой последовательности.
Структурная схема АДМ приведена на рисунке 7.18.
Шаг квантования в этой схеме подчиняется следующему правилу:
, (7.52)
,
где 
- функция текущего и предшествующего кодового слова. Алгоритм выбора множителя М имеет вид
, 
- перегрузка,
, 
- шумы дробления,
.
Действительно при перегрузке последовательности на выходе состоят только из нулей или единиц, а при шуме дробления - чередующейся последовательности нулей и единиц.
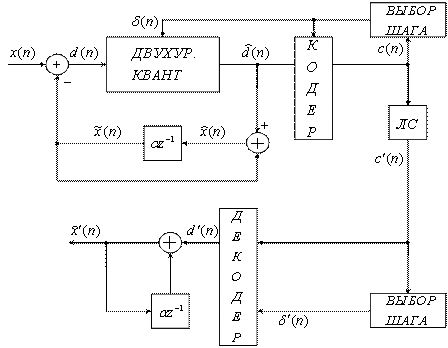
Рисунок 7.18
Исследована зависимость отношения сигнал/шум квантователя от 
(рисунок 7.19).
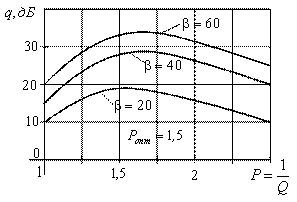
Рисунок 7.19
Сравним системы ЛДМ, АДМ и логарифмической ИКМ (рисунок 7.20) при 
и 
.
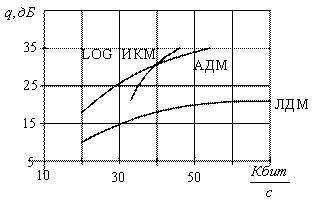
Рисунок 7.20
Проигрыш ЛДМ по сравнению с АДМ составляет 8 – 14 дБ:
т. е. 
дБ, при 
кбит/с 
, а при 
кБ/с 
.
Улучшение качества АДМ достигается путем ее незначительного усложнения, все достоинства ЛДМ при этом сохраняются. Использование предсказателя второго порядка в ЛДМ или АДМ дает выигрыш в отношении сигнал-шум квантования на 4 – 5 дБ.
7.8. Адаптивно-разностная ИКМ (АРИКМ)
7.8.1. Общие замечания
Как следует из пункта 7.6, системы с РИКМ обеспечивают выигрыш в 6 – 12 дБ по сравнению с ИКМ с - компандером. Наибольший выигрыш достигается при переходе от системы без предсказателя к предсказанию 1-го порядка. Это означает, что заданное отношение сигнал-шум квантователя системы с РИКМ можно обеспечить при разрядности меньше на 1 - 2 единицы, чем при ИКМ. Использование квантователя по - закону в разностных схемах (РИКМ) увеличивает отношение сигнал-шум еще на 6 дБ. Характеристики такой системы будут слабочувствительны к уровню входного сигнала, а общая разрядность представления уменьшится на 2 - 3 единицы. Телеметрические и речевые сигналы являются нестационарными, поэтому необходимо использовать адаптивные предсказатели и квантователи. Такие системы называются адаптивно-разностными ИКМ (АРИКМ).
7.8.2. АРИКМ с адаптивным квантованием
Рассмотрим структурную схему АРИКМ с адаптацией по выходному сигналу (рисунок 7.21).
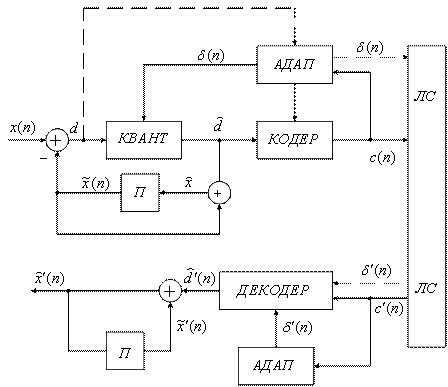
Рисунок 7.21
Систему АРИКМ с адаптивным квантованием можно построить с управлением по входу и выходу, при этом шаг квантования пропорционален среднеквадратическому значению сигнала на его входе и выходе. Можно управлять шагом квантования и по разностному сигналу. Общий выигрыш системы АРИКМ может составлять 18 – 24 дБ по сравнению с адаптивным квантователем с тем же числом уровней. Если применить - закон квантования к разностному сигналу, то выигрыш составит 24 – 30 дБ, что позволит уменьшить разрядность кодового слова на 4 – 5 единиц по сравнению с ИКМ. Дополнительным достоинством является возможность работы с входными сигналами, которые имеют большой динамический диапазон.
7.8.3. АРИКМ с адаптивным предсказателем
Все предыдущие схемы, кроме оптимальных и - квантователей принадлежат к параметрически адаптивным системам. При использовании предсказателей высокого порядка можно ожидать, что РИКМ даст выигрыш 10 – 12 дБ по сравнению с ИКМ. Величина выигрыша зависит от корреляционной формы сигнала, которая изменяется от реализации к реализации. Поэтому целесообразно использовать систему АРИКМ с адаптивным предсказанием, которая позволит дополнительно увеличить отношение сигнал-шум квантователя в случае нестационарных сигналов. При этом необходимо на блоке отсчетов определять оптимальный порядок предсказателя и коэффициенты предсказания 
. Адаптация предсказателя может осуществляться по входному или выходному сигналу.
Структурная схема системы АРИКМ с адаптивным предсказанием изображена на рисунке (рисунок 7.22).
При адаптации по входу для восстановления сигнала в приемнике необходимо передавать 
, 
и 
. Пусть коэффициент предсказания и порядок предсказания зависит от времени. При этом предсказанное значение 
имеет вид:
. (7.53)
При определении коэффициентов 
предполагают, что свойства сигнала не изменяются во времени в течение определенного интервала времени. Для речевого сигнала этот интервал составляет 50 – 100 мс.
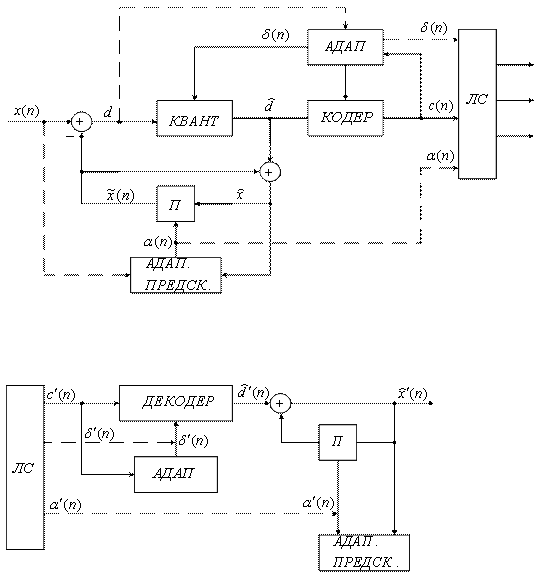
Рисунок 7.22
Рассмотрим зависимости отношения сигнал-шум для адаптивных (АП) и фиксированных (ФП) предсказаний (рисунок 7.23).
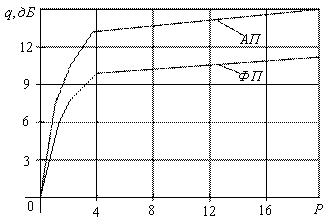
Рисунок 7.23
Верхняя граница отношения сигнал-шум 
при фиксированном предсказании составляет 10 дБ, а при адаптивном предсказании составляет 14 – 15 дБ. При этом чувствительность адаптивного предсказателя к изменению свойств сигнала значительно ниже, чем у фиксированного предсказателя.
7.9. Сравнение цифровых систем кодирования
Сравнение различных систем кодирования производилось при речевых сигналах [4]. Рассмотрим систему:
- Неадаптивной ИКМ с
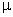- законом квантования. - Адаптивной ИКМ с оптимальным Гауссовским квантованием и управлением по входному сигналу.
- РИКМ с неадаптивным предсказателем первого порядка и адаптивным квантователем с управлением по выходному сигналу.
- АРИКМ с адаптивным предсказателем первого порядка и адаптивным квантователем с управлением по входному сигналу.
- АРИКМ с предсказателем четвертого порядка и адаптивным квантователем с управлением по входному сигналу.
- АРИКМ с предсказателем двенадцатого порядка и адаптивным квантователем с управлением по входному сигналу.
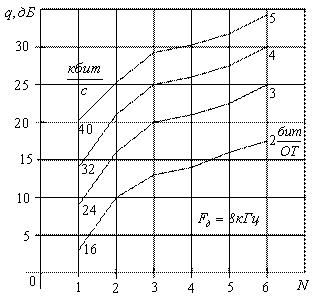
Рисунок 7.24
Кривые отстают друг от друга на 6 дБ. На практике субъективное качество речи сигнала в системе с АРИКМ оказывается лучше, чем с ИКМ при том же отношении сигнал – шум. Обычно 4-х разрядная АРИКМ с адаптивным квантованием оказывается лучше 8-ми разрядной ИКМ с - компандером. Если применять - квантователь для разностного сигнала, то выигрыш АРИКМ дополнительно увеличится на 6 дБ по сравнению с ИКМ и - законом квантования.