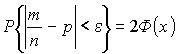1. Теория вероятностей

1.1. Случайное событие

1.2. Алгебра событий (Булева алгебра)

1.3. Вероятность

1.4. Условная вероятность

1.5. Вероятность появления хотя бы одного из события

1.6. Формула полной вероятности

1.7. Формула Бейеса

1.8. Повторение независимых испытаний. Схема Бернулли

2. Случайные величины

2.1. Понятие случайной величины

2.2. Дискретные случайные величины

Задания и решения

1. Теория вероятностей

1.1. Случайное событие

Опыт или случайное событие – действие или ряд действий, который может быть повторен многократно, и который заканчивается не некоторым исходом.

Опыт:

- исход

- пространство элементарных исходов. Все исходы равно возможны.

Случайным событием называется подмножество множества .

Случайным событием называется событие, которое в результате данного опыта может произойти, а может и не произойти.

- называются совместными, если в результате опыта элементарный исход принадлежит и .

- несовместны.

- невозможное событие, если оно не имеет элементарных исходов

- достоверное, если оно в результате опыта обязательно произойдет.

Вероятность случайного события некоторая числовая характеристика или мера этого события.

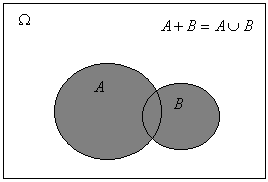
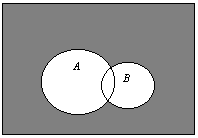
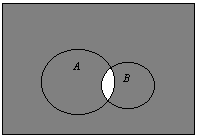
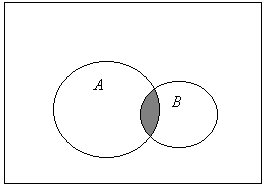
- сумма событий (сложение) – событие состоящие в том, что произойдет A или B или оба.

- это событие, состоящее в том, что произойдет и A и B вместе.

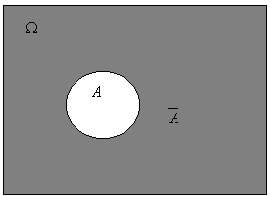
- отрицание события A.

Диаграмма Эйлера-Венна.

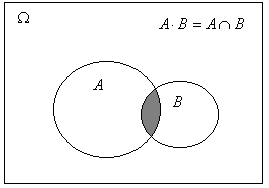
1.2. Алгебра событий (Булева алгебра)

Свойства операций:

• 
• 
• 
• 
• 
• 
• 
• 
• 
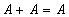
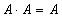
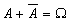
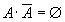
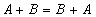
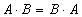
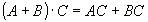
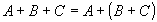
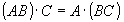
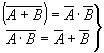• Правило Моргана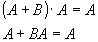
• 

 

 

 

- противоположное событие (отрицание).

Пусть - события, что (несовместимые между собой)

- образуют достоверное событие

- полная группа событий

1.3. Вероятность

Аксиоматическое определение вероятности

Опыт.

ММ,ДМ,МД,ДД

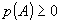• - аксиома не отрицательности.
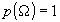• - аксиома нормированности.
• Аксиома одитивности.

, если и несовместны.

- статистическая вероятность(относительная частота события)

- число благоприятных исходов.

- число всего опытов.

Классическая вероятность

- конечное множество состоит из элементарных исходов.

, где - это общее число всех исходов, а - это число благоприятствующих исходов.

Формулы комбинаторики

• Перестановки из 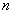элементов - это упорядоченное множество из 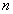элементов, число перестановок .
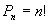• Сочетания из 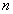элементов по 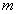элементов - называется подмножества 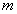элементов из 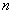, без повторений.

• Размещение из 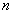элементов по 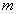- упорядоченное подмножество 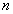элементов из 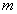элементов.

Схема урн

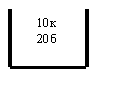
= “2”к и “3”б

= “5”б

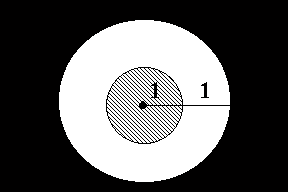
Геометрическая вероятность

1)

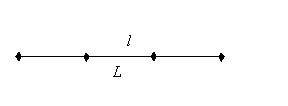
2)

Задача о встрече:

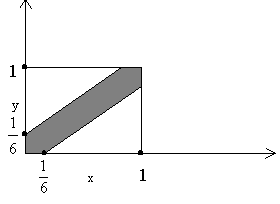
Теорема сложения

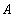1. Пусть и 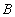- несовместны тогда .
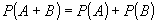2. Пусть и - совместны тогда .

Доказательство:

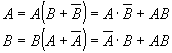
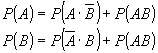
Пример:

- “курит” .

- “живет в общежитии” .

1.4. Условная вероятность

и - называются независимыми, если вероятность события не зависит от того, произошло ли событие и наоборот.

- условная вероятность события при условии, что событие произошло.

Теорема умножения

Если и - независимы, то .

Пример:

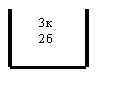
- 1й - б

- 2й - б

Теорема умножения для 3-х событий

Пример:

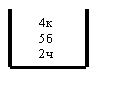
- 1й - б

- 2й - к

- 3й - ч

1.5. Вероятность появления хотя бы одного из события

Опыт:

Двое стреляют

- вероятность попадания 0,8.

- вероятность попадания 0,6.

A - вероятность, что хотя бы один попал.

- оба промаха.

- произошло хотя бы одно событие из .

- ни одно из событий не произошло.

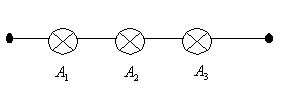
- перегорит лампа.

- цепь не работает.

1.6. Формула полной вероятности

Пусть А – событие, которое происходит при наступлении одного из событий, которые образуют полную группу.

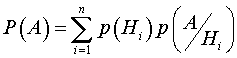
Доказательство:

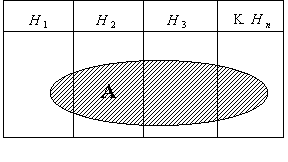
– несовместны

Пусть , тогда

, , …, – гипотезы

Из всех групп выбирается только одна.

Пример:

Идет сдача экзамена

I – 20

II – 10

III – 15

– студент сдал экзамен

– случайно выбранный студент сдал экзамен

1.7. Формула Бейеса

Пусть событие уже произошло, тогда какова вероятность того, что произошло событие .

Полная вероятность 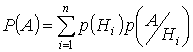, отсюда

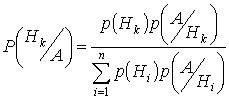
Доказательство:

Пример:

1. 1. 

• 
• 

Полная вероятность

Пусть произошло, тогда

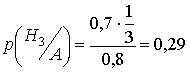
1.8. Повторение независимых испытаний. Схема Бернулли

Испытания независимы, если вероятность элементарных исходов не зависят от предыдущих испытаний.

– число независимых испытаний

– может произойти с вероятностью

С какой вероятностью событие произойдет раз

, где

– вероятность успеха

– вероятность неуспеха

– число сочетаний способов

Доказательство:

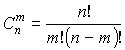
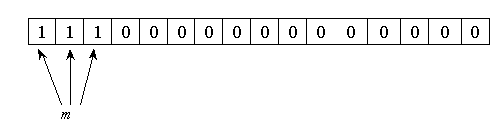
Пример:

10 раз бросим монету, какова вероятность того герб выпадет 5 раз

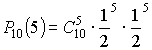
Вероятность того, что событие произойдет от до раз в испытаниях:

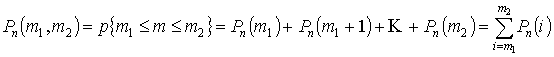
Приближенные формулы в схеме Бернулли.

Локальная теорема Муавра – Лапласа

Если достаточно велико, то вероятность в схеме Бернулли

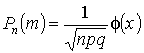, где

– количество испытаний

– вероятность успеха

– вероятность неуспеха

– функция Гаусса

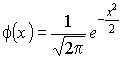, где 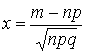, – ожидаемое количество успехов

Пример:

Свойства функции Гаусса:

– четная функция

– наивероятнейшее число успехов

Пример:

Наивероятнейшее число успехов

Интегральная теорема Муавра – Лапласа

 

Пусть – число испытаний (очень велико), тогда

, где

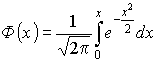– функция Лапласа

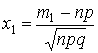
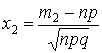
Свойства функции Лапласа:

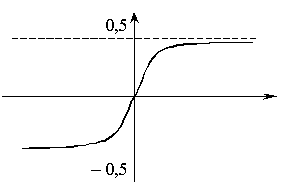
Функция нечетная, то есть

Пример:

1. 
2. 
3. 

1. 1. 

1. 1. 

1. 

– практически достоверно

Правило трех сигм

 

Пример:

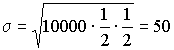
Формула Пуассона

Если достаточно велико, а мало

– среднее значение успехов в испытаниях.

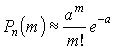, где

Пример:

вызовов в час, какова вероятность того, что в течении 1 мин поступит вызовов.

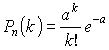
Отклонение частоты вероятности

Пример:

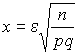
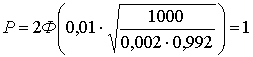
Парадокс раздачи подарков:

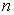1. 1. – человек. Какова вероятность того, что каждому достанется свой подарок.

При

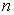1. – подарков, 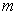– человек. Какова вероятность того, что какой – то человек получит 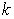подарков.

По формуле Пуассона:

– среднее число подарков

2. Случайные величины

2.1. Понятие случайной величины

Случайной величиной называется величина, которая в результате испытаний принимает то или иное значение.

1. Опыт бросания монеты 2 раза {ГГ, ГР, РГ, РР}
2. Бросание кубика
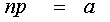
3. Схема Бернулли – 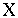число успехов в 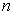испытаниях
4. Стрельба по мишени, 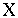– расстояние от точки попадания до центра
5. Группа из 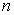человек, 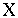– число мальчиков
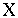6. – время до отказа одного прибора
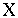7. – вес случайного студента

Дискретные случайные величины – это величины, которые могут принимать конкретное или счетное число значений.

Непрерывные случайные величины – это величины, которые могут принимать несчетное множество значений.

2.2. Дискретные случайные величины

Закон распределения есть соответствие между значениями случайных величин и их вероятностями.

Может задаваться:

1. Таблично

2. Графически

3. Аналитически

1. Таблично

• ряд распределения

В общем виде:

Свойства ряда распределения:

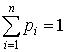– условие нормировки

Пример:

В 2-х бросаниях монеты: – число "гербов"

2. Графически

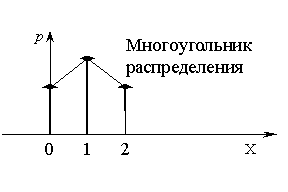
3. Аналитически

Пусть – испытаний

– число успехов

Функция распределения

Свойства функции распределения:

• 
• 
• 
• 
• 
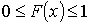
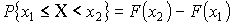
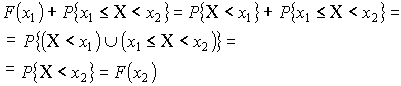
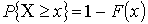
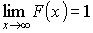
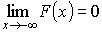
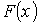• – не убывающая функция
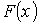• – непрерывна слева

Пусть задан ряд распределения

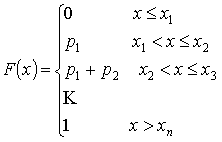
Числовые характеристики дискретных случайных величин.

1. 1. Математическое ожидание 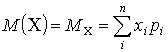– среднее значение

Пример:

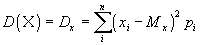
1. 1. Дисперсия

Дисперсия характеризует разброс значений случайной величины от её математического ожидания.

Пример:

1. Среднеквадратическое отклонение (СКО)

Задания и решения

Тема: Случайные события

Методические указания:

 

Основные понятия комбинаторики.

Элементами называются объекты, из которых составлены соединения.

Различают следующие три вида соединений: перестановки, размещения и сочетания.

Перестановками из n элементов называют соединения, содержащие все n элементов и отличающиеся между собой лишь порядком элементов.

Число перестановок из n элементов находится по формуле

где n! (читается “энфакториал”) – произведение натуральных чисел от 1 до n включительно, т. е.

Например,

Размещениями из n элементами по k в каждом (n > k) называются такие соединения, в каждое из которых входит k элементов, взятых из данных n элементов, и которые отличаются друг от друга либо самими элементами, либо порядком их расположения.

Число размещений из n элементов по k находят по формуле

или, пользуясь факториалами,

Например,

Сочетаниями из n элементов по k (n > k) называют соединения, в каждое из которых входит k элементов, взятых из данных n элементов и которые отличаются друг от друга, по крайней мере, одним элементом.

Число сочетаний из n элементов по k находят по формуле

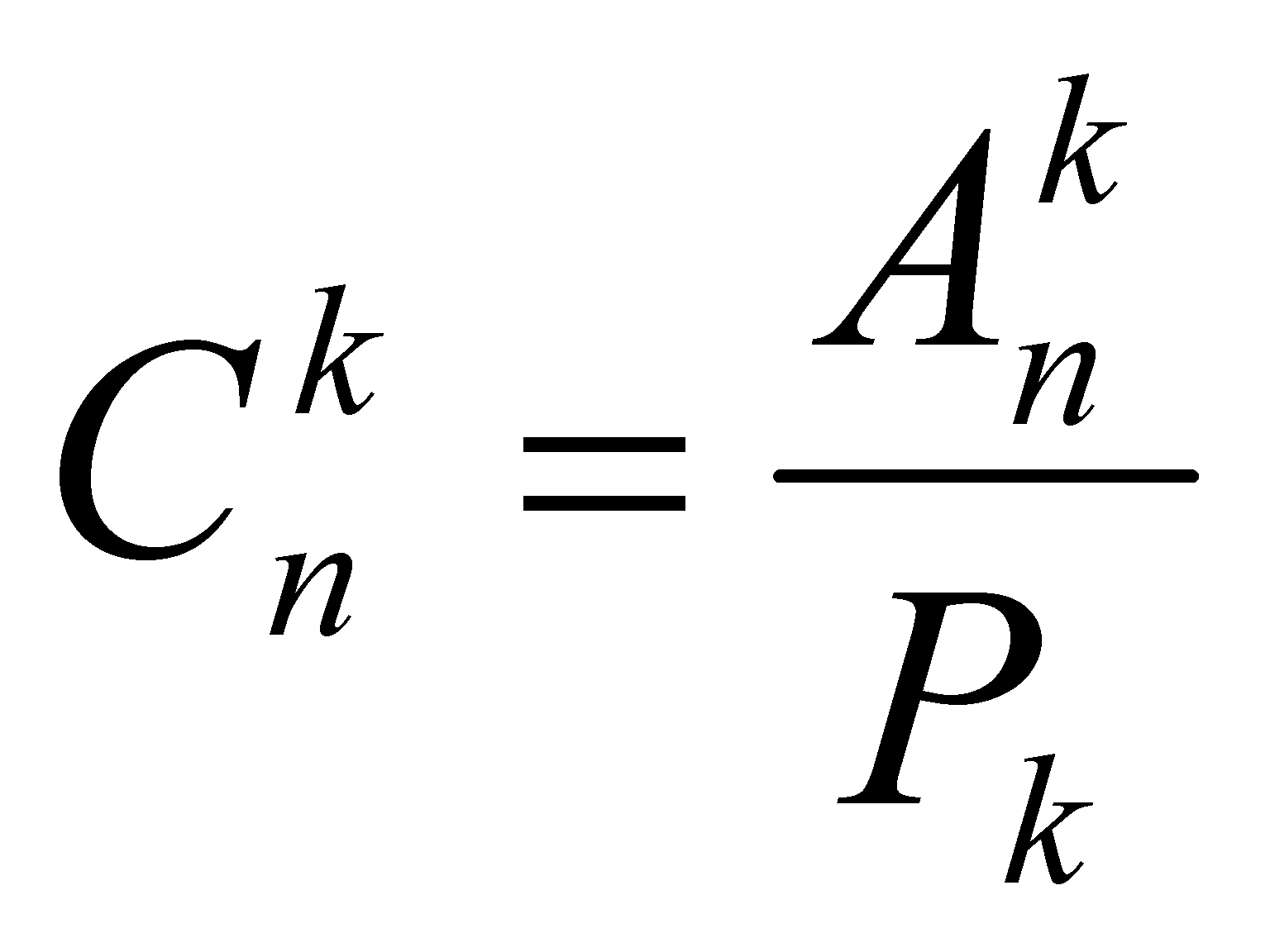
или, пользуясь факториалами,

 

Для упрощения вычислений при полезно использовать следующее свойство сочетаний:

Например,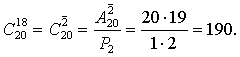

Задача. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: а, м, р, т, ю. Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной и расположенных “в одну линию” карточках можно будет прочесть слово “юрта”.

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 4 карточки из 5, т. е. равно

числу размещений из 5 элементов по 4. Благоприятствует появлению слова “юрта” лишь один исход.

Искомая вероятность равна отношению числа исходов, благоприятствующих появлению события, к числу всех элементарных исходов

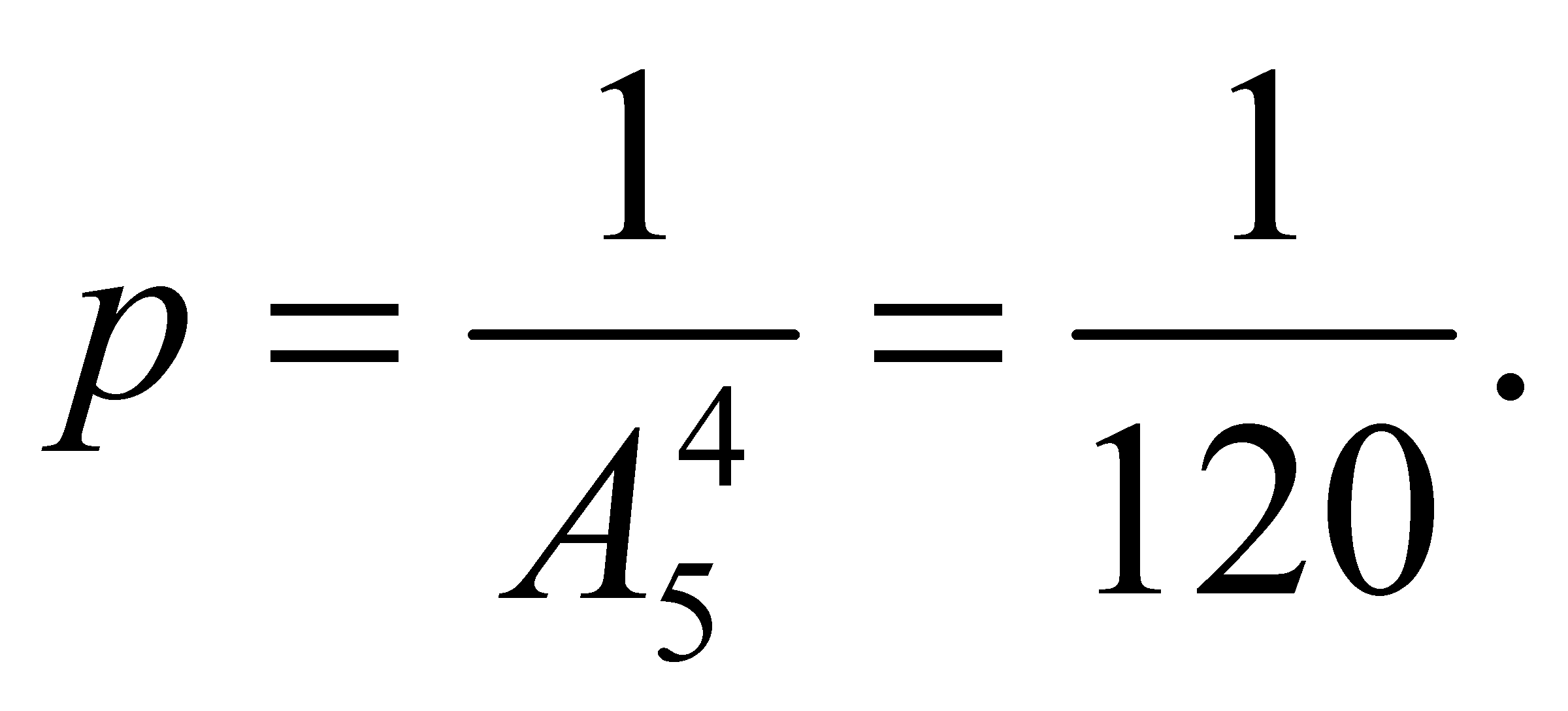
Задача. Вероятность поражения мишени при одном выстреле первым стрелком равна 0,8, а вторым стрелком 0,9. Найти вероятность того, что оба стрелка поразят мишень.

Решение. События А (первый стрелок поразил мишень) и В (второй стрелок поразил мишень) независимые. Искомая вероятность того, что оба стрелка поразят мишень по теореме умножения вероятностей независимых событий равна:

Задача. Для некоторой местности среднее число ясных дней в июле равно 25. Найти вероятность того, что первые два дня июля будут ясными.

Решение. Вероятность того, что первого июля будет ясный день (событие A), равна

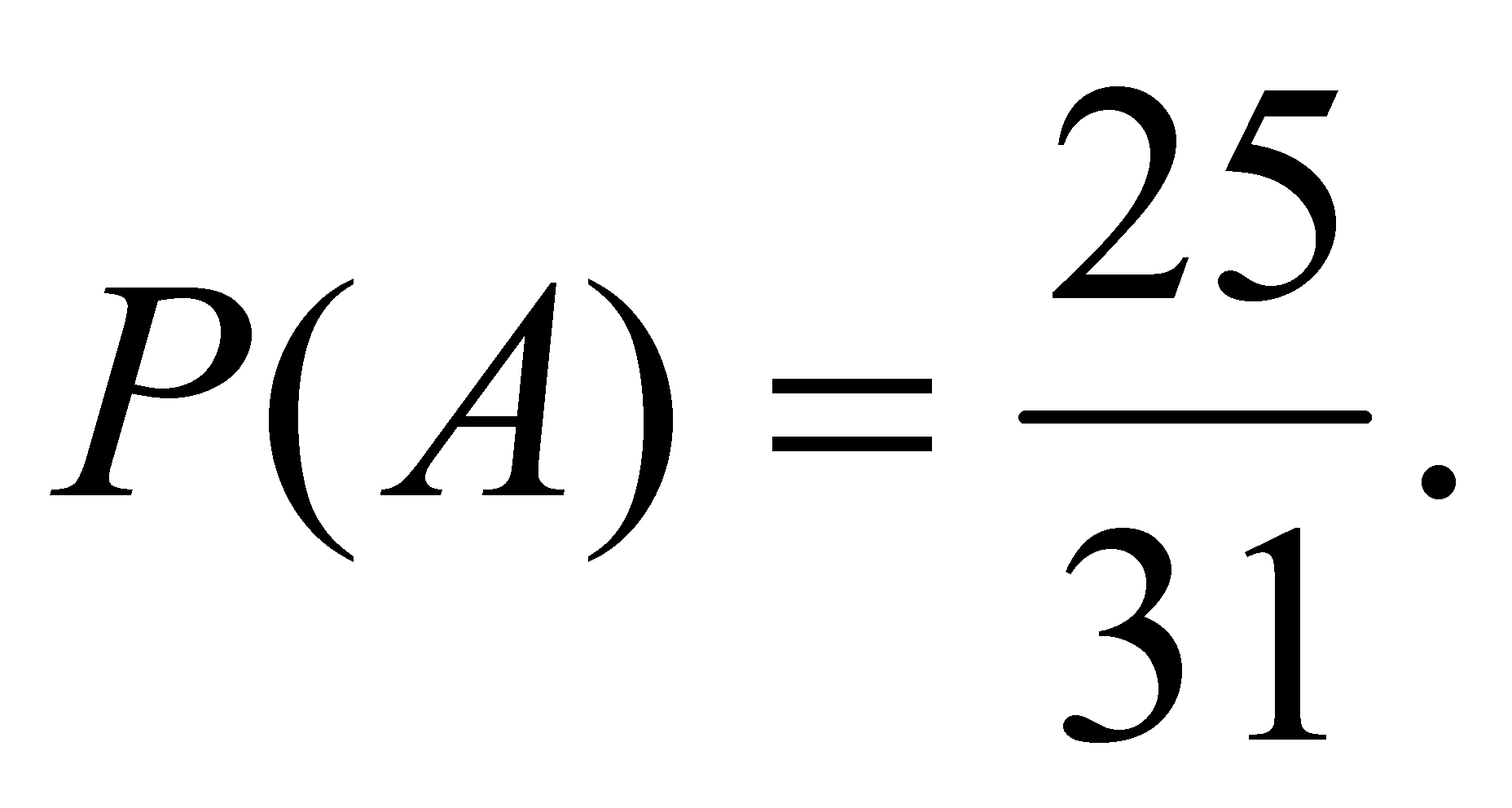
Вероятность того, что второго июля будет ясный день (событие B), при условии, что первого июля также был ясный день, т. е. условная вероятность события В, равна

Искомая вероятность того, что первые два дня июля будут ясными, по теореме умножения вероятностей зависимых событий равна

Задача. Вероятность появления события в каждом из 100 независимых испытаний равна 0,9. Найти вероятность того, что относительная частота отклонится от вероятности появления события (по абсолютной величине) не более чем на 0,03.

Решение. Обозначим искомую вероятность через Р. Воспользуемся формулой

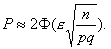
По условию: n=100, e =0,03, p=0,9, q=1-р=1-0,9=0,1. Следовательно,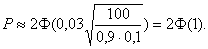

По таблице найдем Ф(1)=0,3413. Искомая вероятность

При решении задач на повторные независимые испытания, в которых вероятности появления события различны, удобно пользоваться производящей функцией вероятностей (через обозначена вероятность того, что в n испытаниях событие появится ровно k раз).

Пусть вероятность появления события в первом испытании равна p1 , во втором – p2 , … , в n-м – pn .

Производящей функцией вероятностей называют функцию, определяемую равенством:

Пусть производят ряд испытаний, причем вероятность появления события в первом испытании равна p1, во втором – p2 и т. д. Тогда вероятность того, что при n испытаниях события появятся ровно k раз, равна коэффициенту при разложении производящей функции по степеням z. Например, если n=2, то

Здесь коэффициент p1 p2 при равен вероятности того, что в двух испытаниях событие появится ровно два раза; коэффициент p1 q2+p2 q1 при z равен вероятности того, что событие появится ровно один раз; свободный член q1 q2 равен вероятности того, что событие не появится ни одного раза.

Задача. Устройство состоит из двух независимо работающих элементов. Вероятность безотказной работы (за время t) первого элемента p1=0,8, а второго p2=0,9. Найти вероятности того, что за время t будут работать безотказно: а) 2 элемента, б) 1 элемент, в) ни один из элементов.

Решение. Так как вероятности безотказной работы элементов равны соответственно 0,8 и 0,9, то вероятности того, что элементы откажут равны: q1=1- 0,8=0,2; q2=1- 0,9=0,1.

Составим производящую функцию:

Вероятность того, что два элемента будут работать безотказно, равна коэффициенту при :

Вероятность того, что 1 элемент будет работать безотказно, равна коэффициенту при z :

Вероятность того, что ни один из элементов не будет работать безотказно, равна свободному члену:

Контроль: 0,72+0,26+0,02=1.

Простейший поток событий.

Одним из основных понятий современных теорий массового обслуживания и надежности является понятие простейшего (пуассоновского) потока.

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Примеры потоков: поступление вызовов на АТС, поступление вызовов на пункт неотложной медицинской помощи, прибытие кораблей в порт, последовательность отказов элементов устройства.

Простейшим называют поток, обладающий свойствами стационарности, отсутствием последействия и ординарности.

Свойство стационарности характеризуется тем, что вероятность появления k событий за время длительностью t не зависит от начала отсчета промежутка времени, а зависит лишь от его длительности. Например, вероятности появления пяти событий на промежутках времени (1; 4), (6; 9), (8; 11) одинаковой длительности t = 3 ед. времени равны между собой.

Свойство отсутствия последействия характеризуется тем; что вероятность появления k событий на любом промежутке времени не зависит от того, сколько событий появилось до начала рассматриваемого промежутка.

Свойство ординарности характеризуется тем, что вероятность появления двух и более событий пренебрежимо мала, сравнительно с вероятностью появления одного события.

Интенсивностью потока l называют среднее число событий, которые появляются в единицу времени. Доказано, что если известна постоянная интенсивность потока l , то вероятность появления k событий простейшего потока за время длительностью t определяется формулой

.

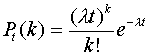Задача. Среднее число заявок, поступающих на АТС в 1 мин равно двум. Найти вероятности того, что за 4 мин поступит а) три вызова, б) менее трёх вызовов, в) не менее трёх вызовов.

Решение1: По условию λ=3, t= 4, k=3. По формуле Пуассона после подстановки получим

.

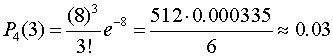Решение2: Найдём вероятность того, что за 4 мин поступит менее трёх вызовов, т. е. ни одного вызова, или один вызов, или два вызова. Поскольку эти события не совместны, применима теорема сложения:

.

Решение3: Найдём вероятность того, что за 4 мин поступило не менее трёх вызовов: так как события “поступило менее трёх вызовов” и “поступило не менее трёх вызовов” - противоположные, то сумма вероятностей этих событий равна единице:

Отсюда: .

Задание:

10.1. В каждой из двух урн содержится 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую. Найти вероятность того, что шар, извлеченный из второй урны, окажется черным.

10.2. В каждой из двух урн содержится 8 черных и 2 белых шара. Из второй урны наудачу извлечен один шар и переложен в первую. Найти вероятность того, что шар, извлеченный из первой урны, окажется черным.

10.3. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,7; для второго и третьего стрелков эти вероятности соответственно равны 0,8 и 0,9. Найти вероятность того, что: а) только один из стрелков поразит цель; б) только два стрелка поразят цель; в) все три стрелка поразят цель.

10.4. Из трёх орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудий эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что: а) только один снаряд попадёт в цель; б) только два снаряда попадут в цель; в) все три снаряда попадут в цель.

10.5. Студент знает 40 из 50 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащиеся в его экзаменационном билете.

10.6. Две команды по 20 спортсменов производят жеребьёвку для присвоения номеров участникам соревнований. Два брата входят в состав различных команд. Найти вероятность того, что братья будут участвовать в соревнованиях под одним и тем же номером 18.

10.7. Два стрелка произвели по одному выстрелу по мишени. Вероятность поражения мишени каждым из стрелков равна 0,9. Найти вероятность того, что: а) оба стрелка поразят мишень; б) оба стрелка промахнутся; в) только один стрелок поразит мишень; г) хотя бы один из стрелков поразит мишень.

10.8. Вероятность хотя бы одного попадания при двух выстрелах равна 0,99. Найти вероятность четырёх попаданий при пяти выстрелах.

10.9. Из аэровокзала отправились 2 автобуса-экспресса к трапам самолётов. Вероятность своевременного прибытия каждого автобуса в аэропорт равна 0,95. Найти вероятность того, что: а) оба автобуса придут вовремя; б) оба автобуса опоздают; в) только один автобус прибудет вовремя; г) хотя бы один автобус прибудет вовремя.

10.10 Две перфораторщицы набили по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,1; для второй перфораторщицы эта вероятность равна 0,2. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась вторая перфораторщица.

11.1. Среднее число вызовов, поступающих на АТС в 1 мин, равно четырём. Найти вероятность того, что за 2 мин поступит: а) 6 вызовов; б) менее шести вызовов; в) не менее шести вызовов. Предполагается, что поток вызовов – простейший.

11.2. Среднее число вызовов, поступающих на АТС в 1 мин, равно двум. Найти вероятность того, что за 4 мин поступит: а) 5 вызовов; б) менее пяти вызовов; в) более пяти вызовов. Предполагается, что поток вызовов – простейший.

11.3. Среднее число кораблей, заходящих в порт за 1 ч, равно трём. Найти вероятность того, что за 4 ч в порт зайдут: а) 6 кораблей; б) менее шести кораблей; в) не менее шести кораблей. Предполагается, что поток кораблей – простейший.

11.4. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 ч, равно четырём. Найти вероятность того, что за 3 ч поступит: а) 6 заявок; б) менее шести заявок; в) не менее шести заявок.

11.5. Среднее число самолётов, прибывающих в аэропорт за 1 мин, равно трём. Найти вероятность того, что за 2 мин прибудут: а) 4 самолёта; б) менее четырёх самолётов; в) не менее четырёх самолётов.

11.6. Вероятность появления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что событие наступит 60 раз в 100 испытаниях.

11.7. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти вероятность того, что в 100 испытаниях событие появится не менее 20 и не более 30 раз.

11.8. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти вероятность того, что событие наступит 12 раз в 100 испытаниях.

11.9. Вероятность наступления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,95 можно было ожидать отклонение относительной частоты появления события от его вероятности не более, чем на 0,04.

11.10. Вероятность наступления события в каждом из независимых испытаний равна 0,8. Произведено 400 испытаний. Найти вероятность того, что относительная частота появления события отклонится от его вероятности не более, чем на 0,09.

В задачах 12.1-12.10 требуется найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение дискретной случайной величины X по заданному закону её распределения, заданному таблично (в первой строке таблицы указаны возможные значения, во второй строке – вероятности возможных значений).

Методические указания:

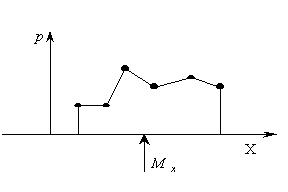
Закон распределения дискретной случайной величины можно изобразить графически. С этой целью на прямоугольной системе координат строят точки M1(x1; p1), M2(x2; p2), …, Mn(xn; pn), где xi – возможные значения случайной величины, а pi – соответствующие вероятности, н соединяют их последовательно отрезками прямых. Полученную фигуру называют многоугольником распределения.

Построим многоугольник распределения дискретной случайной величины X, заданной следующим законом распределения:

X	1	3	5	6
p	0,2	0,4	0,1	0,3

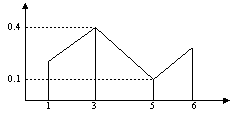
Математическое ожидание: .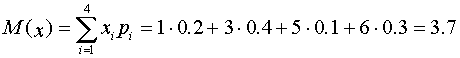

Дисперсия: .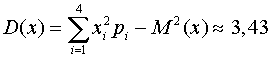

Среднее квадратическое отклонение: .

Задание:

12.1	xi	10	12	20	25	30
	pi	0,1	0,2	0,1	0,2	0,4
12.2	xi	8	12	18	24	30
	pi	0,3	0,1	0,3	0,2	0,1
12.3	xi	30	40	50	60	70
	pi	0,5	0,1	0,2	0,1	0,1
12.4	xi	21	25	32	40	50
	pi	0,1	0,2	0,3	0,2	0,2
12.5	xi	10,2	12,4	16,5	18,1	20,0
	pi	0,2	0,2	0,4	0,1	0,1
12.6	xi	11	15	20	25	30
	pi	0,4	0,1	0,3	0,1	0,1
12.7	xi	12	16	21	26	30
	pi	0,2	0,1	0,4	0,2	0,1
12.8	xi	13	17	22	27	30
	pi	0,1	0,2	0,4	0,2	0,1
12.9	xi	14	18	23	28	30
	pi	0,1	0,4	0,3	0,1	0,1
12.10	xi	15	19	24	29	30
	pi	0,1	0,2	0,2	0,1	0,4

В задачах заданы математическое ожидание а и среднее квадратическое отклонение s нормально распределённой случайной величины X. Требуется найти: а) вероятность того, что X примет значение, принадлежащее интервалу (a , b); б) вероятность того, что абсолютная величина отклонения X-а окажется меньше d.

Методические указания:

Весь материал, относящийся к этому разделу, должен быть изучен наиболее основательно, так как на практике нормально распределенные величины встречаются очень часто.

Дифференциальную функцию нормального распределения и вероятностей смысл параметров этого распределения надо знать наизусть.

Задача. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 2 и 5. Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу

(1; 4).

Решение. Воспользуемся формулой

По условию a =1, b =4, а=2, d =5, следовательно,

Так как функция Лапласа нечетна, то

Таким образом,

По таблице (приложение 2 учебника) находим:

и

Искомая вероятность равна

Задание:

13.1. a=15, s =2, a =9, b =19, d =3.

13.2. a=14, s =4, a =10, b =20, d =4.

13.3. a=13, s =4, a =11, b =21, d =8.

13.4. a=12, s =5, a =12, b =22, d =10.

13.5. a=11, s =4, a =13, b =23, d =6.

13.6. a=10, s =8, a =14, b =18, d =2.

13.7. a=9, s =3, a =9, b =18, d =6.

13.8. a=8, s =4, a =8, b =12, d =8.

14.9. a=7, s =2, a =6, b =10, d =4.

13.10. a=6, s =2, a =4, b =12, d =4.