В основе расчета линейных электрических цепей, находящихся под воздействием периодических негармонических сигналов, лежит принцип наложения. Его суть применительно к негармоническим воздействиям заключается в разложении негармонического периодического сигнала в одну из форм ряда Фурье (см. 5.1. Негармонические периодические сигналы. Разложение в ряд Фурье) и определении реакции цепи от каждой гармоники в отдельности. Результирующая реакция находится путем суперпозиции (наложения) полученных частичных реакций. Таким образом, расчет цепей при периодических негармонических воздействиях включает в себя задачу анализа спектрального состава сигнала (разложение его в ряд Фурье), расчет цепи от каждой гармонической составляющей и задачу синтеза, в результате которого определяется результирующий выходной сигнал как функция времени (частоты) или его действующее (амплитудное значение).

При решении задачи анализа обычно пользуются тригонометрической (5.3) или комплексной (5.6) формой ряда Фурье с ограниченным числом членов разложения, что приводит к некоторой погрешности аппроксимации истинного сигнала. Коэффициенты разложения a_k и b_k в (5.3) или A_k и _k в (5.6) определяются с помощью уравнений (5.4), (5.7) и (5.8). При этом входной сигнал f(a) должен быть задан аналитически. В случае, если сигнал задается графически, например в виде осциллограммы, то для нахождения коэффициентов разложения a_k и b_k можно использовать графоаналитический метод (см. (5.16)).

Расчет цепи от отдельных гармоник ведется обычно символическим методом. При этом необходимо иметь в виду, что на k-й гармонике индуктивное сопротивление X_L(k) = kL, а емкостное сопротивление X_C(k) = 1/(kС), т. е. на k-й гармонике индуктивное сопротивление в k раз больше, а емкостное в k раз меньше, чем на первой гармонике. Этим в частности объясняется то обстоятельство, что высокие гармоники в емкости выражены сильнее, а в индуктивности слабее, чем в приложенном к ним напряжении. Активное сопротивление R на низких и средних частотах можно считать не зависящим от частоты.

После определения искомых токов и напряжений от отдельных гармоник методом наложения находят результирующую реакцию цепи на негармоническое периодическое воздействие. При этом либо определяют мгновенное значение результирующего сигнала на основании расчета амплитуд и фаз отдельных гармоник, либо его амплитудные или действующие значения согласно уравнениям (5.18), (5.19). При определении результирующей реакции необходимо помнить, что в соответствии с представлением периодических негармонических колебаний на комплексной плоскости векторы различных гармоник вращаются с различной угловой частотой.

Пример. К цепи, изображенной на рис. 5.6, приложено напряжение u(t) в форме прямоугольных импульсов с периодом повторения T = 2t_и и амплитудой A_и = 1В (см. рис. 5.3, б). Определить мгновенное и действующее значения напряжения на емкости.

Разложение данного напряжения в ряд Фурье определяется по формуле (5.31). Ограничимся первыми тремя членами разложения (5.31):

Таким образом, приложенное напряжение содержит постоянную составляющую U₀ = 1/2, первую U₁ = 4/ и третью U₃ = 4/(3) гармоники с нулевыми начальными фазами. Найдем напряжение на емкости от постоянной составляющей приложенного напряжения U₀: .

Комплексное действующее напряжение от первой гармоники

Токи I₂₍₁₎ или I₃₍₁₎ можно найти по формуле разброса. Например, для I₃₍₁₎ имеем:

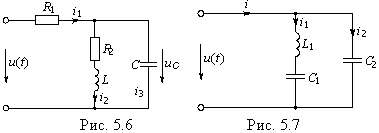
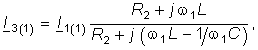где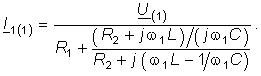

Аналогичным образом находится напряжение на емкости от 3-й гармоники: где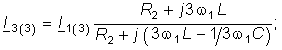

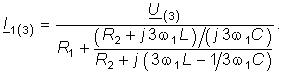
После нахождения комплексных действующих значений напряжений на емкости отдельных гармоник и выделения в них модулей U_C(1), U_C(3) и фаз _C1 = arg U_C(1), _C3 = arg U_C(3) записывает мгновенное значение напряжения на емкости в форме суммы (ряда): .

Действующее значение напряжения определяем согласно (5.19)

При анализе резонансных явлений в электрических цепях при периодических несинусоидальных воздействиях следует иметь в виду, что резонанс напряжений и токов может достигаться на разных гармониках. При этом, как и ранее, резонансом на k-й гармонике называется такое состояние электрической цепи, состоящей из разнохарактерных реактивных элементов, при котором фазовый сдвиг между входным током и приложенным напряжением k-x гармоник равен нулю. Явление резонанса может быть использовано для выделения отдельных гармоник из периодического несинусоидального сигнала. Следует подчеркнуть, что в цепи может одновременно быть достигнут резонанс токов на одной частоте и резонанс напряжений на другой.

Пример. Для цепи, изображенной на рис. 5.7, при заданной ₁, L₁ найти значение C₁ и C₂, при которых одновременно возникает резонанс напряжений на 1-й и резонанс токов на 5-й гармонике.

Из условия резонанса напряжений находим, что входное реактивное сопротивление цепи на первой гармонике должно равняться нулю: 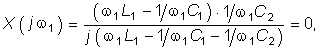(5.32)

а на пятой — бесконечности (входная реактивная проводимость на пятой гармонике должна быть равна нулю): 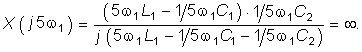(5.33)

Из условий (5.32) и (5.33) находим искомое значение емкостей: