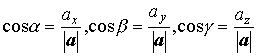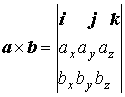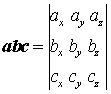|
Наименование |
Обозначение, формула |
|
Вектор и его выражение в декартовых координатах |
a=ax i+ay j+az k=(ax, ay, az) |
|
Модуль (длина) вектора |
|
|
Направляющие косинусы вектора |
|
|
Сложение двух векторов |
a+b=(ax+bx, |
|
Умножение вектора на скаляр |
ka=(kax, |
|
Скалярное произведение двух векторов |
|
| Скалярное произведение в декартовых координатах |
ab=axbx+ayby+azbz |
|
Условие ортогональности двух ненулевых векторов |
ab=0 |
|
Векторное произведение двух векторов |
|
|
Векторное произведение в декартовых координатах |
|
|
Условие коллинеарности двух ненулевых векторов |
|
|
Смешанное произведение трех векторов |
|
|
Смешанное произведение в декартовых координатах |
|
|
Условие компланарности трех ненулевых векторов |
abc=0 векторы (лежат в одной плоскости) |
| Линейно независимая система векторов | {a1,a2,…,an} - линейно независима 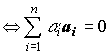 только при условии только при условии |
2. Векторная алгебра
- Категория: Справочник по Высшей математике