6.1. Электродинамические потенциалы

6.2. Элементарный электрический излучатель

6.2.1. Ближняя и дальняя зоны

6.3. Мощность излучения элементарного излучателя. Сопротивление излучения

6.4. Элементарный магнитный излучатель. Принцип перестановочной двойственности

6.1. Электродинамические потенциалы

Рассмотрим четвертое уравнение Максвелла . Формально в соответствии с правилами векторного анализа:

(6.1.1)

на основании этого тождества вектор можно представить как rot другого любого вектора :

(6.1.2)

Возьмем второе уравнение Максвелла:

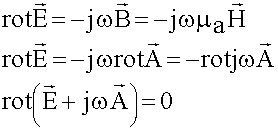(6.1.3)

Появился новый вектор, rot которого равен нулю.

- тождество известное. (6.1.4)

Мы можем утверждать, что выражение в скобках есть градиент.

(6.1.5)

(6.1.6)

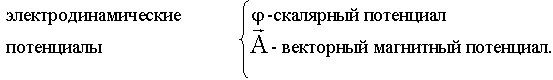
Можно найти уравнения, из которых определяются и .

На f для постоянного тока при w = 0 вклад в электрическое поле от вектора не происходит:

(6.1.7)

Для статистических и стационарных процессов электрическое поле представляется как градиент некоторой скалярной функции .

В случае переменных полей:

(6.1.8)

Получим уравнение для определения величин и . Воспользуемся первым уравнением Максвелла, через обозначим сторонние

источники:

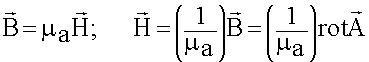
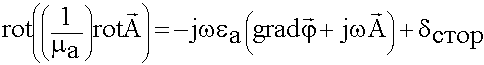(6.1.9)
(6.1.10)

Используем тождество:

(6.1.11)

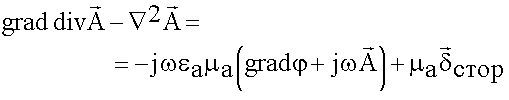
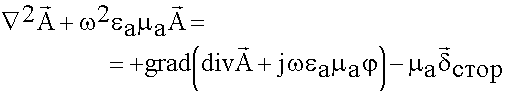(6.1.12)

Для упрощения уравнений используем свойство электродинамических потенциалов – их неоднозначность:

(6.1.13)

В силу неоднозначности мы можем ввести требование. Налагаем дополнительное требование:

калибровочное соотношение (6.1.14)

для электродинамических потенциалов. Это соотношение имеет четкий физический смысл. Строго можно доказать, что соотношение является другой записью закона сохранения заряда. Все другие допустимые соотношения будут противоречить закону сохранения заряда (требуется дополнительное время для доказательства).

- неоднородное волновое уравнение

Гельмгольц для (6.1.15)

Получим по такой же схеме второе соотношение из второго уравнения Максвелла:

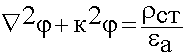- неоднородное волновое уравнение Гельмгольца для . (6.1.16)

При отсутствии источников ЭМП, правая часть обращается в 0, уравнения будут однородными, их называют уравнениями Гельмгольца. Не решая уравнений, мы будем записывать решение исходя их физического смысла.

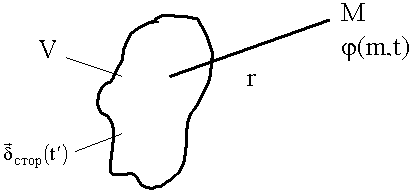
Источниками ЭМП являются заряды, 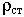распределенные в некоторой области V. Найдем потенциал в точке М. Выделим элементарный объем заряженного тела. Найдем потенциал, который создает этот объем.

Объем настолько мал, что заряд можно считать точечным.

Полный потенциал найдем как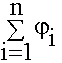

;

;

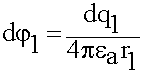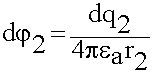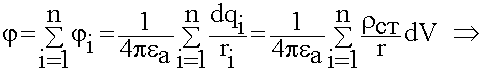
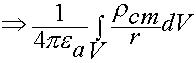
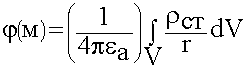(6.1.17)

Распределение потенциала не зависит от времени.

Некоторое тело содержит заряды 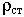, имеющие зависимость от времени. При расчете изменяющихся от времени процессов необходимо учитывать конечную скорость распространения. Момент времени регистрации будет другим:

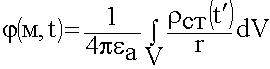
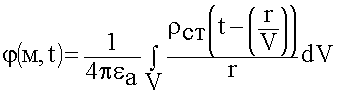
(6.1.18)

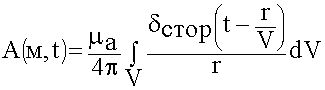
Решение волновых уравнений, их называют запаздывающими электродинамическими потенциалами.

6.2. Элементарный электрический излучатель

Рассмотрим простейший источник, короткая проволока с переменным током.

Под элементарным электрическим излучателем будем понимать проводник достаточно малых размеров по сравнению с с равномерным по амплитуде распределения тока. Будем считать, что излучатель находится в безграничном пространстве, в идеальной среде без потерь (вакуум). При расчете полей введем ограничения:

• безограниченная среда (вакуум)
• 1 < < , такое условие позволяет пренебречь запаздыванием внутри излучателя, т.е. амплитуда тока постоянна, хотя ток переменный. На концах диполя будут скапливаться заряды.
• r > > 1 размеры излучателя много меньше расстояний, на которых определяются потенциалы.

1. переменный ток в излучателе изменяется по гармоническому закону.

Если разобраться с полями, которые создает элементарный излучатель, то можно рассчитать поля самой сложной антенны. Расчет полей элементарных излучателей будем проводить в сферической системе координат.

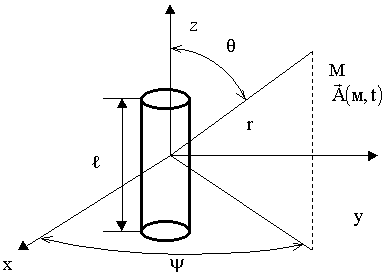
Этапы решения:

1. 1. Определение векторного электродинамического потенциала, создаваемого излучателем .
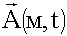   2. Определение вектора Н.

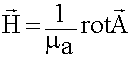
1. Определение электрического поля из второго уравнения:

Расчет полей элементарного излучателя

Первый этап:

Расчет вектора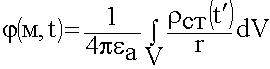

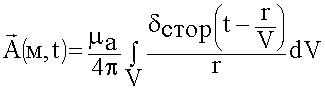
Как использовать данный результат к элементарному проводу?

Используем сферическую систему координат.

r > > 1, т.к. r очень большое, и примерно везде одинаково, выносим за знак интеграла:

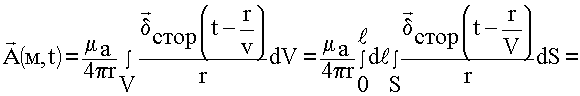
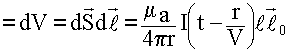
- умножение необходимо на единичный вектор, т.к. ток имеет направление.

Поскольку процессы гармонические, необходимо ввести зависимость от времени:

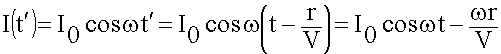
(обозначим). Это строго можно показать!

В теме “Плоские волны” будет сделано.

С учетом всех обозначений переходим к комплексным выражениям:

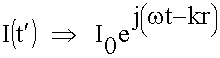
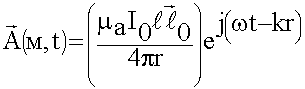
Из общих выражений, которые дает теория, мы получили конечный результат.

Второй этап. Определение магнитных полей.

- определяем вектор , т.е. магнитное поле.

; ;

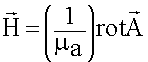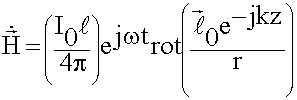
окончательный результат. Из 3-х составляющих, который определяют rot, отличный от 0 будет только азимутальная составляющая Нy . Не решая:

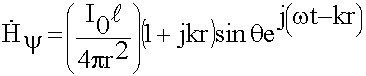
Н_r = Hq = 0 (6.2.1)

Третий этап: Нахождение электрических полей.

rot (первое уравнение Максвелла)

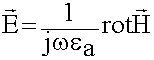
Запишем составляющие электрического поля, их две:

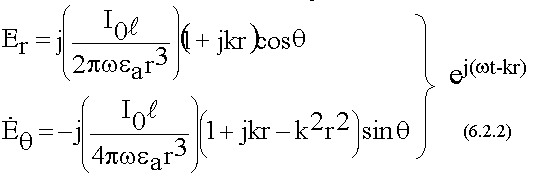
Формулы запоминать не надо, они нужны для дальнейшего анализа.

Для элементарного излучателя характерно наличие 3-х составляющих полей

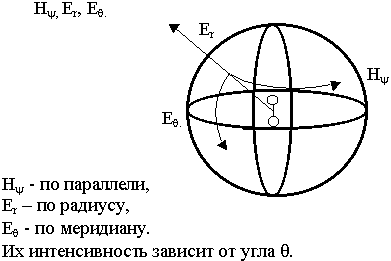
Элементарный излучатель создает в окружающем пространстве сферическую волну, поверхностью равных фаз является сфера.

6.2.1. Ближняя и дальняя зона электрического излучателя

Критерием для ближней и дальней зоны является величина kr. Если kr < < 1, то ближняя зона, если kr > > 1 – дальняя зона.

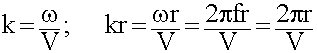; kr << 1 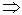r < <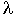

В ближней зоне расстояние r < < .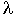

В дальней зоне расстояние r > > 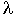. (6.2.1.1)

Поля в ближней зоне

• kr < < 1 анализируем общие выражения.

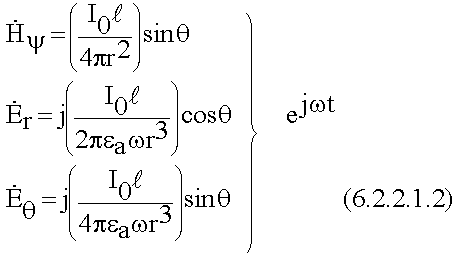
Анализ:

1. Поля очень быстро уменьшаются с удалением от излучателя.
2. Электрические и магнитные поля отличаются на множитель j, если в такой то момент магнитное поле max, то электрическое поле минимально, т.е. электрическое и магнитное поле по фазе сдвинуто на 90⁰.

В ближней зоне процесс протекает, но ничего не изменяется, не излучается, колебательный процесс, пол периода поля как бы отрываются от излучателя, полпериода вновь возвращается.

Поля в дальней зоне.

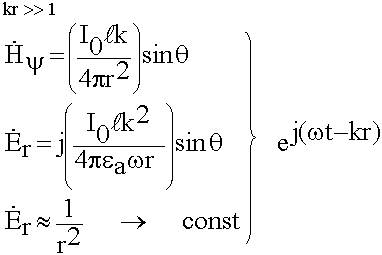
Анализ. Радиальная составляющая изменяется обратно пропорционально квадрату расстояния , поэтому в дальней зоне она очень мала 0.

Составляющие 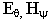убывают более медленно с расстоянием .

С ростом частоты напряженности поля увеличиваются при прочих равных условиях. В дальней зоне отношение

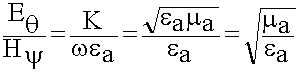
определяется только параметрами среды и называется характеристическим волновым сопротивлением. По размерности это ОМ.

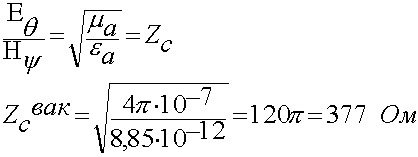
Пример:

Если замерили напряженность магнитного поля в дальней зоне Н = 1 А/м, Е = 377 В/м.

По мере удаления от излучателя сферическая волна переходит в плоскую. В дальней зоне будет плоская электромагнитная волна.

Направленность излучения. Интенсивность излучения зависит от угловых координат.

Графическое изображение распределения в пространстве электрического (магнитного) полей в полярных координатах называется диаграммой направленности.

6.3. Мощность излучения элементарного излучателя

Вопросы по мощности излучения автоматически решаются, если определены составляющие полей. Расчет имеет смысл только в дальней зоне:

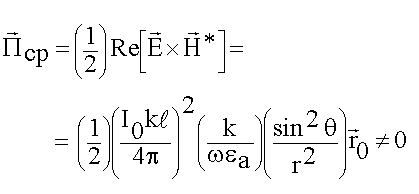(6.3.1)

В дальней зоне излучатель излучает. Не странно ли? В ближней зоне П_ср = 0, а в дальней зоне П_ср 0. Фаза в ближней зоне 90⁰, а в дальней зоне они совпадают. Излучение вызвано тем, что электрические и магнитные поля изменяются в фазе. Во всех излучателях ДН по мощности всегда уже чем ДН по напряженности.

Выясним, каково значение и куда направлена мощность излучения?

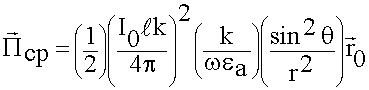
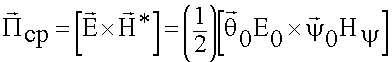(6.3.2)

Энергия от элементарного излучателя направлена по радиусу:

Рассчитаем мощность, отдаваемую в окружающее пространство.

Средняя мощность это поток вектора через замкнутую поверхность за период:

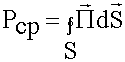(6.3.3)

Удобнее всего выбрать в качестве поверхности сферу

;

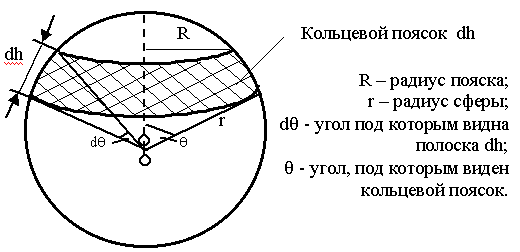
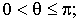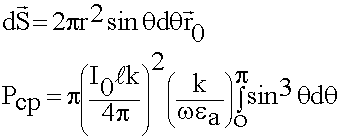
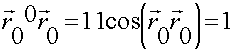
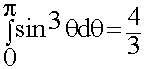- табличный интеграл

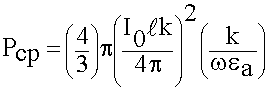(6.3.4)

В дальнейшем будем считать, что излучатель находится в вакууме:

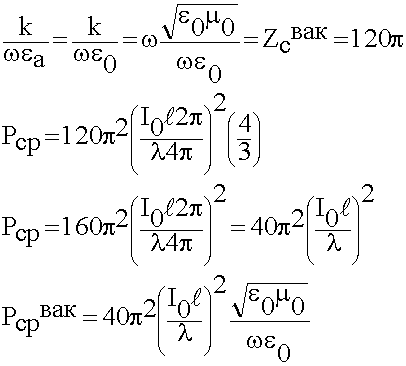(6.3.5)

Для характеристики излучателя удобнее ввести параметр, не зависящий от тока, но характеризующий излучающие способности излучателя. В качестве такого параметра выбирают сопротивление излучения:

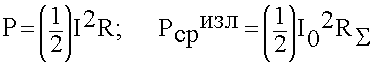
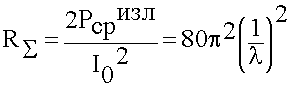(6.3.6)

Если антенна имеет 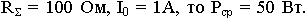. Сопротивление излучения зависит только от размеров и для повышения излучающей способности антенны надо увеличивать ее размеры, либо повышать частоту, т.е. укорачивать .

6.4. Элементарный магнитный излучатель. Принцип перестановочной двойственности

Под элементарным магнитным излучателем будем понимать замкнутый проводник с током, настолько малым, что амплитуда переменного тока во всех сечениях проводника считается неизменной.

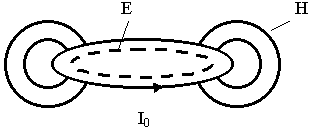
Все условия сохраняются, как и при анализе элементарного электрического излучателя.

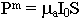
Будем использовать накопленный материал. Что общего между элементарным электрическим излучателем и магнитным? Качественно попытаемся изобразить картину поля, которую создает элементарный магнитный излучатель. Небольшая фантазия. Предположим, что имеются элементарные носители магнитных зарядов. Поскольку их на самом деле нет, то их называют фиктивными.

1. 1. Поле, создаваемое фиктивным зарядом

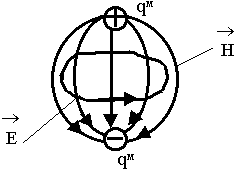
1. 1. Поле, создаваемое электрическим зарядом q^э

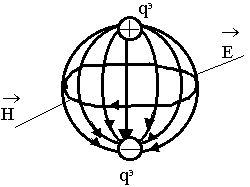
Из качественного рассмотрения картины поля видно, что структура полей, создаваемых электрическими и магнитными зарядами отличается заменой линий

Установим правила перехода от полей, создаваемыми электрическими зарядами к полям, создаваемыми магнитными зарядами. Это правило в теории поля называют принципом перестановочной двойственности.

Электрические источники

Магнитные источники

Из анализа уравнений

(6.4.2)

Принцип перестановочной двойственности

Определим поля элементарного магнитного излучателя с помощью принципа перестановочной двойственности. Для электрического излучателя (дальняя зона):

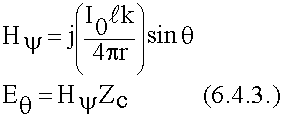
По определению:

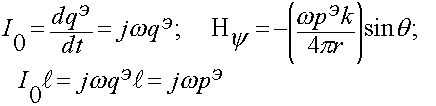
Для магнитного излучателя:

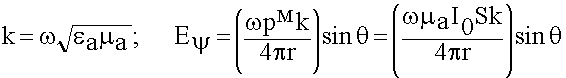
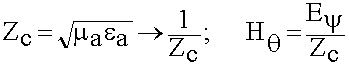
Сопротивление излучения у элементарных магнитных излучателей значительно меньше, чем у элементарных электрических излучателей. Почему?

Излучение – это токи смещения. Если система открытая, то токам легче открываться. Iпр

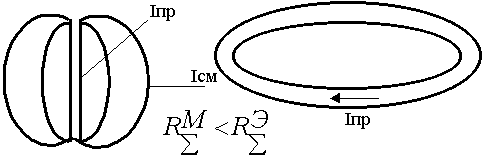
На практике используется комбинация штыря и витка, т.к. ориентация на “0” очень четкая (охота на лис).

Диаграмма направленности кардиоида

Максвелл в своих трудах утверждал, что окружающая среда и вакуум необходимы для существования токов смещения, так же как и проводники для токов проводимости. В конце 70-х годов прошлого столетия Гельмгольц поручает ученику Герцу провести опыты, опровергающие теорию Максвелла. Никаких приборов не было. Герц считал, что если ЭВМ отсутствуют, то эксперимент должен провалиться (а он этого хотел).

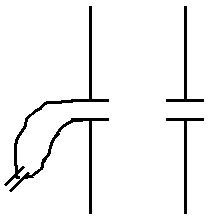
Две проволоки на некотором расстоянии друг от друга. Через некоторое время после разряда на одном из проводов Герц обнаружил искры у другой проволоки. Герц поставил экран, затем призму, пересчитал все, и оказалось то, о чем давно говорил Максвелл. Сам Герц написал о том, что надо запретить использовать его открытия для связи. Антенны для низкочастотных колебаний получались огромных размеров (испытания проводились на низких частотах). Попытаемся сделать расчеты. Изучение раздела “Излучение” начнем с понятия электродинамических потенциалов.