1. Основные понятия

1.1. Понятия базы данных, системы баз данных, системы управления базами данных

1.2. Классификация моделей данных

2. Реляционные модели данных

2.1. Реляционные объекты данных

2.1.1. Домены

2.1.2. Отношения

2.2. Целостность реляционных данных

2.2.1. Потенциальные, первичные и альтернативные ключи

2.2.2. Внешние ключи

2.2.3. Null-значения

2.3. Реляционная алгебра

2.3.1. Язык SQL

2.3.2. Основные операторы реляционной алгебры

2.3.3. Дополнительные операторы реляционной алгебры

2.3.4. Операции обновления

2.3.5. Значение реляционной алгебры

3. Проектирование реляционных БД

3.1. Функциональные зависимости

3.1.1. Понятие функциональной зависимости

3.1.2. Правила вывода функциональных зависимостей

3.1.3. Неприводимые функциональные зависимости

3.1.4. Диаграммы (схемы) функциональных зависимостей

3.2. Нормализация отношений

3.2.1. Обзор нормальных форм

3.2.2. Декомпозиция без потерь

3.2.3. Первая, вторая и третья нормальные формы

3.2.4. Нормальная форма Бойса-Кодда

3.3. Нормальные формы более высокого порядка

3.3.1. Многозначные зависимости

3.3.2. Четвертая нормальная форма

3.3.3. Зависимость соединения

3.3.4. Пятая нормальная форма

3.4. Итоговая схема процедуры нормализации

1. Основные понятия

1.1. Понятия базы данных, системы баз данных, системы управления базами данных

В широком смысле слова база данных (БД) – это совокупность сведений о конкретных объектах реального мира в какой-либо предметной области.

Для удобной работы с данными их необходимо структурировать, т.е. ввести определенные соглашения о способах их представления.

В реальной деятельности в основном используют системы БД.

Системы БД существуют и на малых, менее мощных компьютерах, и на больших, более мощных. На больших применяют в основном многопользовательские системы, на малых – однопользовательские.

Однопользовательская система (single-user system) – это система, в которой в одно и то же время к БД может получить доступ не более одного пользователя.

Многопользовательская система (multi-user system) - это система, в которой в одно и то же время к БД может получить доступ несколько пользователей.

Основная задача большинства многопользовательских систем – позволить каждому отдельному пользователю работать с системой как с однопользовательской.

Различия однопользовательской и многопользовательской систем – в их внутренней структуре, конечному пользователю они практически не видны.

Система баз данных содержит четыре основных элемента: данные, аппаратное обеспечение, программное обеспечение и пользователи.

Данные в БД являются интегрированными и общими.

Интегрированные – значит, данные можно представить как объединение нескольких, возможно перекрывающихся, отдельных файлов данных. (Например, имеется файл, содержащий данные о студентах – фамилию, имя, отчество, дату рождения, адрес и т.д., а другой – о спортивной секции. Необходимые данные о студентах, посещающих секцию, можно получить путем обращения к первому файлу.)

Общие – значит, отдельные области данных могут использовать различные пользователи, т.е. каждый из этих пользователей может иметь доступ к одной и той же области данных, даже одновременно. (Например, одни и те же данные БД о студентах может одновременно использовать студенческий отдел кадров и деканат.)

К аппаратному обеспечению относятся:

• Накопители для хранения информации вместе с подсоединенными устройствами ввода-вывода, каналами ввода-вывода и т.д.
• Процессор (или процессоры) вместе с основной памятью, которая используется для поддержки работы программного обеспечения системы.

Между собственно данными и пользователями располагается уровень программного обеспечения. Ядром его является система управления базами данных (database management system – DBMS), или диспетчер БД (database manager).

Основная функция СУБД – это предоставление пользователю БД возможности работы с ней, не вникая в детали на уровне аппаратного обеспечения. Т.е. все запросы пользователя к БД, добавление и удаление данных, выборки, обновление данных – все это обеспечивает СУБД.

Иными словами, СУБД поддерживает пользовательские операции высокого уровня. Сюда включены и операции, которые можно выполнить с помощью языка SQL.

SQL - это специальные язык БД. Сейчас он поддерживается большинством СУБД, он является официальным стандартом языка для работы с реляционными системами. Название SQL вначале было аббревиатурой от Structured Query Language (язык структурированных запросов), сейчас название языка уже не считается аббревиатурой, т.к. функции его расширились и не ограничиваются только созданием запросов.

СУБД – это не единственный программный компонент системы, хотя и наиболее важный. Среди других – утилиты, средства разработки приложений, средства проектирования, генераторы отчетов и т.д.

Пользователей СБД можно разделить на три группы:

• Прикладные программисты. Отвечают за написание прикладных программ, использующих БД. Для этих целей применимы различные языки программирования. Прикладные программы выполняют над данными стандартные операции – выборку, вставку, удаление, обновление – через соответствующий запрос к СУБД. Такие программы бывают простыми – пакетной обработки, или оперативными приложениями – для поддержки работы конечного пользователя.
• Конечные пользователи. Работают с системами БД непосредственно через рабочую станцию или терминал. Конечный пользователь может получить доступ к БД, используя оперативное приложение или интегрированный интерфейс самой СУБД (такой интерфейс тоже является оперативным приложением, но встроенным). В большинстве систем есть хотя бы одно такое встроенное приложение – процессор языка запросов (или командный интерфейс). Язык SQL – пример языка запросов для БД. Кроме языка запросов в современных СУБД, как правило, есть интерфейсы, основанные на меню и формах – для непрофессиональных пользователей. Понятно, что командный интерфейс более гибок, содержит больше возможностей.
• Администраторы БД. Отвечают за создание БД, технический контроль, обеспечение быстродействия системы, ее техническое обслуживание.

СУБД имеют свою архитектуру. В процессе разработки и совершенствования СУБД предлагались различные архитектуры, но самой удачной оказалась трехуровневая архитектура, предложенная исследовательской группой ANSI/SPARC американского комитета по стандартизации ANSI (American National Standards Institute). Упрощенная схема архитектуры СУБД приведена на рис. 1.

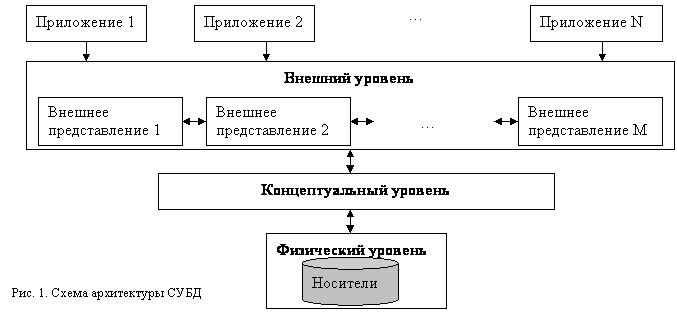
Внешний уровень – это уровень пользователя. По сути, это совокупность внешних представлений данных, которые обрабатывают приложения и какими их видит пользователь на экране. Это может быть таблица с отсортированными данными, с примененным фильтром, форма, отчет, результат запроса. Внешние представления взаимосвязаны, т.е. из одного внешнего представления можно получить другое.

Концептуальный уровень – центральный. Здесь БД представлена в наиболее общем виде, который объединяет данные, используемые всеми приложениями. Т.е. это обобщенная модель предметной области, для которой созданы БД. Можно сказать, что концептуальный уровень формируется при создании таблиц (определение их полей, типов, свойств), связей, а так же при заполнении таблиц.

Физический уровень – собственно данные, расположенные на внешних носителях.

1.2. Классификация моделей данных

Ядром любой БД является модель данных.

Т.к. СУБД имеет 3-х уровневую архитектуру, то понятие модели данных связано с каждым уровнем.

Физическая модель данных связана с организацией внешней памяти и структур хранения, используемых в данной операционной среде.

На концептуальном уровне модели данных наиболее важны для разработчиков БД, т.к. именно ими определяется тип СУБД.

Для внешнего уровня отдельных моделей данных нет, они лишь являются подсхемами концептуальных моделей данных.

Кроме моделей данных, соответствующих трем уровням архитектуры СУБД, существуют предшествующие им, не связанные с компьютерной реализацией. Они служат переходным звеном от реального мира к БД. Это класс инфологических (семантических) моделей.

Общая классификация моделей данных приведена на рис. 2.

МОДЕЛИ ДАННЫХ

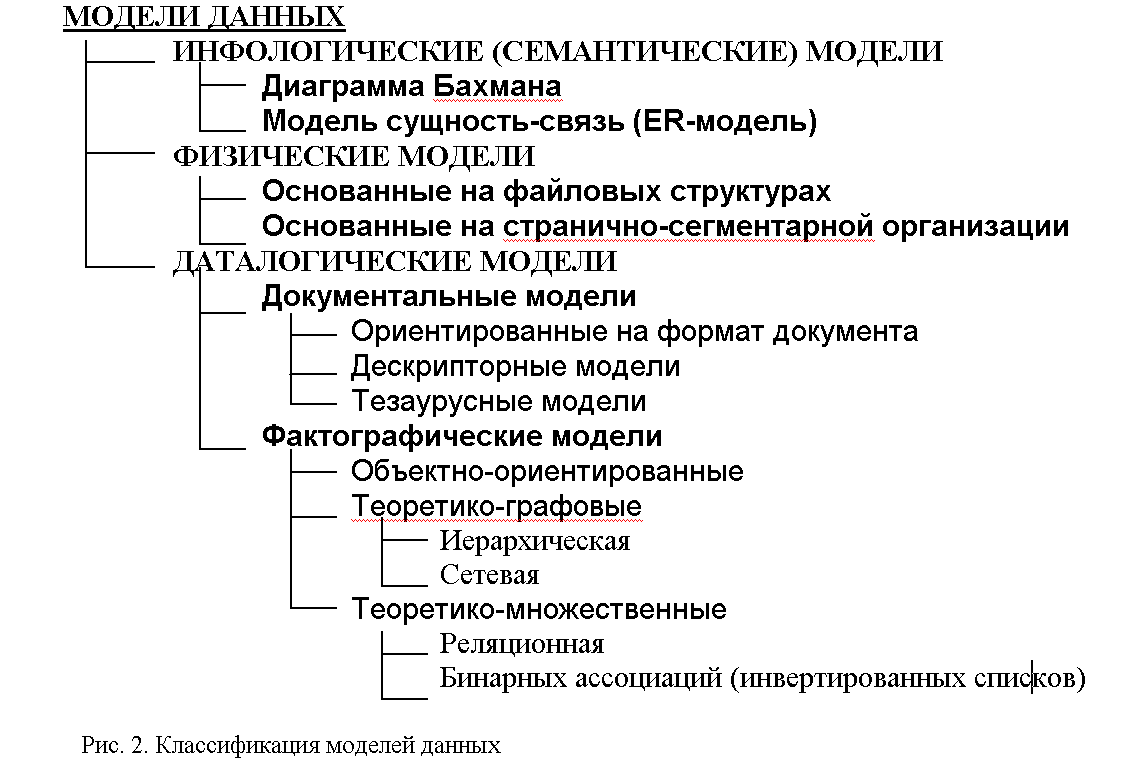
Инфологические (семантические) модели данных используются на ранних стадиях проектирования БД.

Даталогические модели данных уже поддерживаются конкретной СУБД.

Физические модели данных связаны с организацией данных на носителях.

Документальные модели данных соответствуют слабоструктурированной информации, ориентированной на свободные форматы документов на естественном языке.

Модели данных, ориентированные на формат документа, связаны со стандартным общим языком разметки SGML (Standart Generaliset Markup Language), а также HTML, предназначенным для управления процессом вывода содержимого документа на экран.

Дескрипторные модели данных – самые простые, широко использовались раньше. В них каждому документу соответствует дескриптор – описатель, который имеет жёсткую структуру и описывает документ в соответствии с заранее определенными характеристиками.

Тезаурусные модели данных основаны на принципе организации словарей. Содержат языковые конструкции и принципы их взаимодействия в заданной грамматике. Эти модели используются, например, в системах-переводчиках.

Объектно-ориентированная модель перекликается с семантическими моделями данных. Принципы похожи на принципы объектно-ориентированных языков программирования. Структура таких моделей графически представима в виде дерева, узлами которого являются объекты. Свойства объектов описываются типом.

Объекты иерархическоймодели данных связанны иерархическими отношениями и образуют ориентированный граф. Основные понятия иерархических структур: уровень, узел (совокупность свойств данных, описывающих объект), связь.

В сетевой модели данных при тех же основных понятиях (уровень, узел, связь) каждый элемент может быть связан с любым другим элементом.

В реляционной модели данных данные представлены только в виде таблиц.

Мы будем рассматривать именно реляционные модели данных, т.к. в последнее время реляционные СУБД заняли преимущественное положение, поскольку их недостатки связаны в основном с техническими проблемами и компенсируются ростом быстродействия и ресурсов памяти современных ЭВМ.

2. Реляционные модели данных

2.1. Реляционные объекты данных

Существует специальная терминология, принятая в теории реляционных БД (рис. 3)

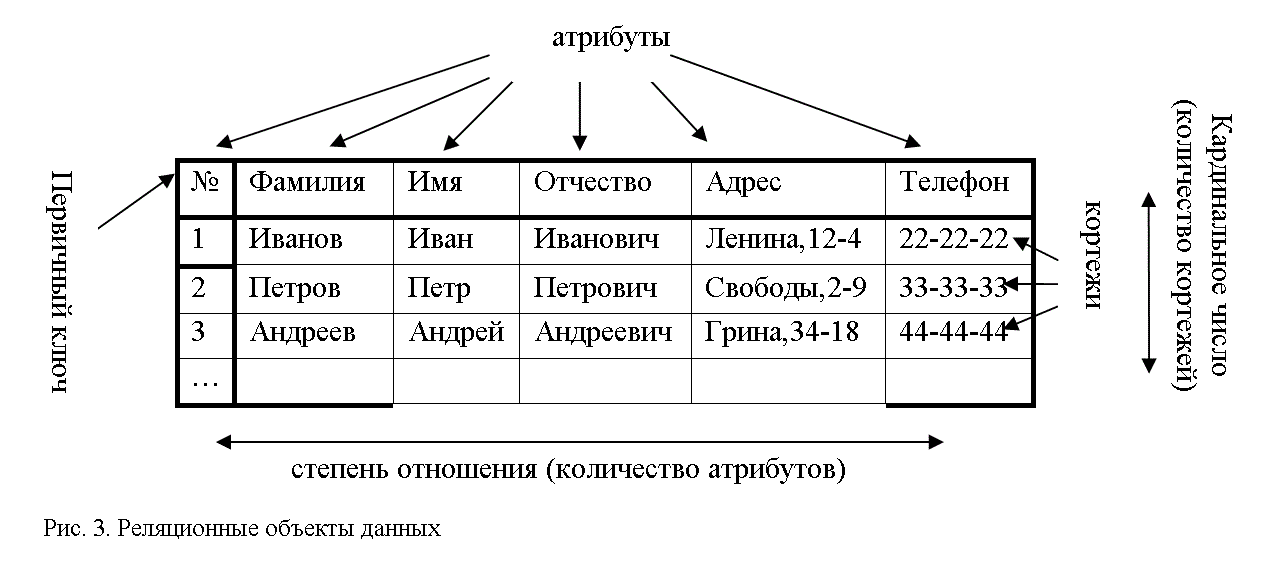
Отношением называется вся таблица, отвечающая определенным свойствам (о которых более подробно – ниже).

Отношение характеризуется следующими понятиями:

Атрибут соответствует столбцу этой таблицы, а именно – свойствам объектов, сведения о которых хранятся в ней. В конкретных СУБД атрибуты часто называют полями.

Первичный ключ – это атрибут (или множество атрибутов), значения которого уникально идентифицируют кортежи (записи).

Кортеж соответствует заполненной строке таблицы. В конкретных СУБД кортежи называют записями.

Степень отношения – количество его атрибутов.

Кардинальное число – количество кортежей в отношении в текущий момент времени.

Домен – это общая совокупность значений, из которой берутся конкретные значения для конкретного атрибута.

2.1.1. Домены

Домены более точно можно определить как именованное множество скалярных значений одного типа. Эти скалярные значения называют скалярами. По сути, это наименьшая семантическая (смысловая) единица данных. У скаляров нет внутренней структуры, т.е. они не разложимы в данной реляционной модели.

Например, если имеется атрибут (свойство объекта) «ФИО», он предусматривает скаляры, содержащие фамилию, имя и отчество. Конечно, эти скаляры можно еще разбить на буквы, но тогда будет утрачен нужный смысл. То есть для данной модели наименьшими семантическими единицами данных будут именно фамилия, имя и отчество.

Из доменов, как уже говорилось, берутся значения атрибутов. На практике домены часто не описывают, а задают типом, форматом и другими свойствами данных. Каждый атрибут должен быть определен на единственном домене.

Основное назначение доменов — ограничение сравнения различных по смыслу атрибутов.

Например: Если для атрибутов №ЗачетнойКнижки отношения Студенты и №Кабинета для отношения Кабинеты домены заданы следующим образом:

№ зачетной книжки = {100000, 100001, 100002, … 999999}

№ кабинета = {1, 2, 3, … 999},

то система выдаст ошибку на запрос типа: «Вывести всех студентов, № зачетной книжки которых совпадает с № кабинета». Если же домены не определены, а определен только целый тип данных для атрибутов №ЗачетнойКнижки и №Кабинета, то подобный запрос выполнится, хотя не будет иметь смысла.

Еще одно возможное применение доменов – использование их в специальных запросах. Например, «Какие отношения в БД включают атрибуты, определенные на домене «№ зачетной книжки»?». В системе, поддерживающей домены, такой запрос будет иметь смысл и результатом его будет список отношений, где используется № зачетной книжки (это могут быть отношения Студенты,Занятия,Успеваемость, …). А в системе, где домены не определены, реализовать такого рода запрос гораздо сложнее – если через имена атрибутов, то они могут не совпадать (имена атрибутов, содержащих № зачетной книжки могут варьироваться: № зачетки, № зачетной книжки и т.п.), а если через тип – то получится много лишних отношений, т.к. немало атрибутов может иметь целый тип данных.

2.1.2. Отношения

С отношением связаны понятия переменной отношения и значения отношения.

Переменная отношения — обычная переменная, т.е. именованный объект, значение которого может изменяться со временем (по сути - это множество заданных атрибутов данного отношения).

Значение отношения — значение переменной отношения в конкретный момент времени (по сути - это сохраненные кортежи отношения).

Дадим более точное, формальное, определение отношения.

Например, рассмотрим отношение Студенты БД Факультет:

Заголовок: {№ЗачетнойКнижки : Целый; Фамилия : Текстовый; Имя : Текстовый; ДатаРождения : Дата; Адрес : Текстовый; Группа : Текстовый}

Тело: {№ЗачетнойКнижки : 111111; Фамилия : Петров; Имя : Петр; Отчество : Петрович; ДатаРождения : 12.03.83; Адрес : Свободы, 12-45; Группа : ИНФ-21}

{№ЗачетнойКнижки : 222222; Фамилия : Иванов; Имя : Иван; Отчество : Иванович; ДатаРождения : 25.11.83; Адрес : Ленина, 65-9; Группа : ИНФ-21}

и т.д.

Для упрощенного описания отношения и его атрибутов будем использовать следующую запись:

ИмяОтношения (ИмяАтрибута1, ИмяАтрибута2, …, ИмяАтрибутаN),

где будем подчеркивать атрибуты, входящие в первичный ключ и где N – степень отношения.

Свойства отношений

1. Нет одинаковых кортежей. Это следует из того, что тело отношения определено как математическое множество кортежей, а множество по определению не содержит одинаковых элементов.

Следствие этого свойства: в отношении всегда существует первичный ключ.

2. Кортежи неупорядочены. Это следует также из того, что тело отношения определено как математическое множество кортежей. А математическое множество по определению не упорядочено. Именно поэтому в отношении не существует таких понятий, как «следующий», «предыдущий», «второй кортеж» и т.п.

3. Атрибуты не упорядочены. Это следует из того, что заголовок отношения определен как математическое множество атрибутов. А множество не упорядочено по определению. Т.е. опять нет понятий «первый атрибут», «следующий атрибут» и т.п.

4. Все значения атрибутов неделимы. Это следствие того, что каждый атрибут определен на своем домене, а домен – множество неделимых скаляров.

2.2. Целостность реляционных данных

В любой момент времени любая БД содержит некоторые определенные значения атрибутов, которые выражает конкретное состояние объекта реального мира. Следовательно, БД нуждается в определении правил целостности, необходимых для того, чтобы данные не вступили в противоречие с реальным миром. Такие правила целостности являются специфическими для каждой БД. Это, по сути, информирование СУБД об ограничениях реального мира, Например, имя – только текстовое значение, значения веса, роста - только положительные и т.п.

Но таких правил целостности недостаточно – не менее важно, чтобы данные внутри самой БД не противоречили друг другу.

Например, в БД Факультет случайно указали, что Иванов Петр учится в группе ИНФ-15, но такой группы на данном факультете нет. Или для того же Петра группу указали правильно – ИНФ-13, но в качестве ФИО ее старосты написали Сидорова Н.М., а на самом деле старостой ИНФ-13 является Андреева С.В.

Для предотвращения подобных ситуаций существуют общие правила целостности реляционных данных. Эти правила связаны с первичными и внешними ключами.

2.2.1. Потенциальные, первичные и альтернативные ключи

Например, в отношении Студенты базы данных Факультет потенциальным ключом может являться один из атрибутов №ЗачетнойКнижки, НомерЛичногоДела или НомерПаспорта, т.к. каждый из них удовлетворяет определению. Но неверно будет назначить потенциальным ключом этого отношения множество нескольких из этих атрибутов, т.к. хотя для такого множества выполняется свойство уникальности, но не выполняется свойство неизбыточности.

Потенциальные ключи предназначены для обеспечения основного механизма адресации на уровне кортежей, т.е. по значению потенциального ключа можно однозначно найти кортеж. В СУБД Access потенциальные ключи называются также индексированными полями (для них в свойстве поля Индексированное поле указывается значение «Да»).

Базовое отношение может иметь несколько потенциальных ключей, но один их них должен быть выбран в качестве первичного ключа. Остальные же потенциальные ключи будут называться альтернативными. Например, в таблице Специальности базы данных Факультет может существовать два потенциальных ключа: ШифрСпециальности и НазваниеСпециальности. Если первичным ключом назначить ШифрСпециальности, тогда альтернативным ключом будет НазваниеСпециальности.

В СУБД Access для первичного ключа значением свойства Индексированное поле указывается значение «Да (совпадения не допускаются)», а для альтернативного может быть такое же или «Да (совпадения допускаются)».

В любом отношении должен быть первичный ключ, значит должен содержаться хотя бы один потенциальный ключ. Это может быть одно поле, а может быть множество нескольких или даже всех полей отношения (в этом случае отношение называется полностью ключевым).

Если же в отношении нет естественных потенциальных ключей или они неудобны для использования в рамках создаваемой БД, то вводят искусственные ключи. Например, в отношении Преподаватели базы данных Факультет можно ввести поле КодПреподавателя, чтобы не использовать номер паспорта, номер личного дела или табельный номер.

2.2.2. Внешние ключи

В базах данных отношения могут быть связаны друг с другом. Например, в БД Факультет отношение Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы) связано с отношением Группы (КодГруппы, Специальность, Курс, Староста). Значение атрибута КодГруппы в отношении Студенты допустимо только в том случае, если такое значение имеется в качестве значения первичного ключа отношения Группы. В этом случае атрибут КодГруппы в отношении Студенты является внешним ключом, ссылающимся на первичный ключ – КодГруппы отношения Группы.

Внешний ключ существует для обеспечения непротиворечивости данных внутри БД, т.е. значение внешнего ключа не может быть таким, которого нет среди значений первично ключа связанной таблицы.

В реляционной БД предусмотрена связь внешнего ключа не только с первичным, но и с любым другим потенциальным ключом, т.е. с альтернативным. Но нельзя создавать дублирующие связи – и с первичным, и с альтернативным – чтобы избежать избыточности данных.

Некоторые замечания по этому определению:

1. Каждое значение внешнего ключа должно является значением соответствующего потенциального ключа, однако, обратное не требуется, т.е. потенциальный ключ, соответствующий внешнему ключу может содержать значения, которые в данный момент не являются значением внешнего ключа. Например, может существовать запись о группе, в которую пока никто из студентов не зачислен.

2. Данный внешний ключ будет составным тогда и только тогда, когда соответствующий потенциальный ключ также будет составным. Аналогично – внешний ключ будет простым (состоящим из одного атрибута) тогда и только тогда, когда соответствующий потенциальный ключ – простой. Например, пусть в БД Факультет имеются отношения Занятия (КодГруппы, Дисциплина, Преподаватель) и Расписание (№Недели, ДеньНедели, №пары, КодГруппы, Дисциплина, Преподаватель, Кабинет). Здесь внешний ключ отношения Расписание {КодГруппы, Дисциплина, Преподаватель} - составной, как и соответствующий первичный ключ в отношении Занятия.

3. Каждый атрибут, входящий в данный внешний ключ должен быть определен на том же домене, что и соответствующий атрибут соответствующего потенциального ключа.

4. R₁ и R₂ не обязательно различны Например, …..

С понятием внешнего ключа связывается еще ряд терминов:

Можно сказать, что значение внешнего ключа является ссылкой к кортежу, содержащему соответствующее значение потенциального ключа. Этот кортеж называется ссылочный (целевой) кортеж, а содержащее его отношение – ссылочное (целевое). Отношение, содержащее внешний ключ называется ссылающимся отношением.

С внешними ключами связано одно из основных правил целостности.

По сути, это правило эквивалентно определению внешнего ключа.

Правила внешних ключей

Правило ссылочной целостности подразумевает состояние БД в конкретный момент времени. Но как избежать временных некорректных ситуаций, которые могут возникнуть при обновлении данных в БД?

Самый простой путь – запретить любые операции, приводимые к нарушению правила ссылочной целостности.

Но при обновлении БД не избежать временного нарушения целостности (Например, расформировывается группа или в начале учебного года переименовывается группа). Поэтому необходимо ввести компенсирующие операции, которые «исправят» это временное нарушение целостности.

Такие компенсирующие операции связаны с внешними ключами, поэтому для любого внешнего ключа при создании связи необходимо ответить на два вопроса:

1) Что должно произойти при попытке удалить объект ссылки внешнего ключа? (Например, убрать все группы 5 курса из таблицы Группы в конце года) Возможны как минимум два варианта ответов на этот вопрос:

a) ограничить, т.е. не удалять, пока пользователь не удалит ссылающиеся кортежи, т.е. отложить удаление;

b) каскадировать, т.е. удалить, удаляя все соответствующие ссылающиеся кортежи.

2) Что должно произойти при попытке изменить (обновить) значение потенциального ключа, на который имеется ссылка? (Например, заменить названия группы ИНФ-11 на ИНФ-21 в таблице Группы в начале учебного года). Также возможны два варианта:

a) ограничить, т.е. отложить до удаления значений ссылающихся кортежей;

b) каскадировать, т.е. обновить во всех ссылающихся кортежах.

Выбор ответов на эти два вопроса и является заданием (или определением) правил внешних ключей. В СУБД MS Access определение правил внешних ключей осуществляется при создании связей между таблицами: если будет отмечен параметр Каскадное обновление связанных полей, то выбрана операция каскадирование для обновления, если не отмечен – ограничение; аналогично с параметром Каскадное удаление связанных записей.

2.2.3. Null-значения

Осложнения при обеспечении целостности данных могут быть вызваны неопределенными или отсутствующими значениями. Например, в БД по произведениям искусства не известен автор картины; в БД Школа некоторые дети – сироты (нет родителей) и т.п.

Для решения проблем отсутствия значений Кодд предложил ввести специальные метки, названные им Null-значениями, которые определил так: если данный кортеж имеет Null-значение данного атрибута, то это означает, что в нем значение атрибута отсутствует.

Это не то же, что числовой 0 или пробел, это вообще не значение, а только метка – обозначение отсутствия любого значения.

Большинство современных реляционных СУБД поддерживают Null-значения.

С Null-значениями связано второе правило целостности.

Это правило объясняется следующим: кортежи отношений соответствуют объектам реального мира; по определению эти объекты различимы, т.е. некоторым образом опознаваемы; первичные ключи выполняют функцию уникальной идентификации объектов; если невозможно идентифицировать объект, то нельзя сказать существует ли он вообще.

Необходимо сделать некоторые уточнения по этому правилу:

1) это правило касается только базовых отношений (т.е. не вычисляемых, не производных);

2) правило применимо только для первичных ключей, а для альтернативных ключей Null-значения могут быть запрещены или разрешены.

Применение Null-значений для внешних ключей:

• Когда нет данных, т.е. нет соответствующего кортежа в ссылочном отношении (Например, нет данных о родителях ученика);
• При каскадном удалении. (Например, на факультете расформировали одну из групп, а студентов этой группы распределяют в другие, но пока точно не известно в какие. Тогда при каскадном удалении этой группы из таблицы Группы удалятся также все студенты этой группы из таблицы Студенты. Но их не надо удалять, поэтому для этих студентов временно заменяют значение атрибута КодГруппы в отношении Студенты на Null-значения.

Некоторые разработчики БД стараются избегать Null-значений, применяя вместо этого значения по умолчанию. Но в Access, как и во многих современных СУБД, поддерживается Null-значения.

2.3. Реляционная алгебра

Реляционная алгебра состоит из набора операторов, использующих отношения в качестве операндов, результатом операций при этом также являются отношения.

2.3.1. Язык SQL

Реляционные операции реализуются на языке SQL. Действующим на данный момент стандартом является принятая Американским национальным институтом стандартов (ANSI) версия SQL92.

В СУБД Microsoft Access используется язык Access SQL (Jet SQL), который немного отличается от стандартной версии, но основные операторы и правила - стандартные.

Как и любой язык программирования, язык SQL имеет свои правила записи инструкций. Основные из них:

1. Запятая используется для разделения элементов списков. Например, списка имен полей.
2. Для задания имен полей, которые содержат недопустимые символы (например, пробел), используются квадратные скобки. Например, [Дата Рождения].
3. Если в запрос включены поля нескольких таблиц, то используется полное имя поля, которое состоит из имени таблицы и имени поля, разделенных точкой. Например, Студенты.Фамилия.
4. Символьные строки заключаются в апострофы или кавычки.
5. В конце инструкции ставиться точка с запятой (;).
6. В инструкциях SQL, разбитых на несколько строк, можно использовать отступы, которые указывают на продолжение предыдущей строки.

Основным видом запроса на SQL является SELECT – запрос на выборку. Его общий вид:

SELECT <список имен полей> (если все поля, то *)

FROM <имя таблицы>

[WHERE <условия выбора>] (можно использовать <, >, =, BETWEEN, AND, NOT, OR)

[GROUP BY <имена полей>] (группировка)

[ORDER BY <имена полей>] (сортировка)

Примеры:

1) Вывести из таблицы Студенты имя, фамилию, адрес и телефон, отсортировав по фамилии

SELECT Фамилия, Имя, Адрес, Телефон

FROM Студенты

ORDER BY Фамилия;

2) Вывести все поля таблицы Студенты, произведя группировку по группам

SELECT *

FROM Студенты

GROUP BY Группа;

3) Вывести всех студентов из таблицы Студенты, проживающих на улице Ленина

SELECT *

FROM Студенты

WHERE left([Адрес], 9)=’ул.Ленина’;

4) Выбрать студентов из таблицы Студенты, которые родились в сентябре 1985 года

SELECT *

FROM Студенты

WHERE [Дата Рождения] between 31.08.85 and 1.10.85;

2.3.2. Основные операторы реляционной алгебры

Реляционная алгебра, определенная Коддом, состоит из 8 операторов. Их можно разделить на две группы: реляционные операции, аналогичные традиционным операциям над множествами, и собственно реляционные операции.

Для всех реляционных операций необходимо выполнение свойства замкнутости, т.е. результатом каждой операции над отношениями должно являться отношение.

Реляционные операторы, аналогичные традиционным операциям над множествами:

1) Объединение. Результатом объединения отношений R₁ и R₂ является отношение R₃, содержащее все кортежи, которые принадлежат хотя бы одному из R₁ и R₂.

В отличие от объединения множеств, результатом является не множество кортежей, а именно отношение. Поэтому кортежи должны быть однородны, т.е. объединяемые отношения должны быть совместимы по типу. Это значит, что:

a) каждое из них имеет одно и то же множество атрибутов;

b) соответствующие атрибуты определены на одном и том же домене.

На языке SQL: R₁ UNION R₂

Например: допустим, в БД Факультет имеются отдельные отношения Лаборанты и Преподаватели. Эти две таблицы можно объединить, в результате получиться отношение, содержащее все данные на сотрудников факультета: и преподавателей, и лаборантов.

2) Пересечение. Результатом пересечения отношений R₁ и R₂ является отношение R₃, содержащее кортежи, принадлежащие и R₁, и R₂. Для этой операции также должно выполняться условие совместимости по типу.

НаязыкеSQL: R₁ Intersect R₂

Например: допустим, что в БД Факультет есть отношения Лаборанты и Студенты. С помощью этой операции можно найти тех студентов, которые работают лаборантами.

3) Вычитание. Результатом вычитания отношения R₂ из отношения R₁ является отношение R₃, все кортежи которого принадлежат R₁ и не принадлежат R₂. Условие совместимости по типу также должно выполняться.

На языке SQL:R₁ Minus R₂

Например, из тех же отношений Лаборанты и Студенты базы данных Факультет можно выяснить, какие студенты не работают лаборантами на факультете и наоборот.

4) Произведение (декартово). Результатом произведения отношений R₁ и R₂ является отношение R₃, содержащее все возможные кортежи, которые являются сочетанием двух кортежей, принадлежащих

R1		R2		R3
a		x		a	x
b		y		a	y
c				b	x
				b	y
				c	x
				c	y

5) соответственно отношениям R₁ и R₂.

На языке SQL:R₁ TIMES R₂

Результатом является отношение, а не множество пар кортежей, как это бывает при произведении над множествами. Первоначальные кортежи сцепляются, т.е. образуют в результате новый кортеж.

Например, если выполнить произведение отношений Студенты и Дисциплины, то получим в результате отношение, в котором будет содержаться информация о том, что каждый студент изучает каждую дисциплину.

Собственно реляционные операторы:

5) Выборка (операцией ограничения). Результатом выборки, примененной к отношению R₁, является отношение R₂, содержащее все кортежи отношения R₁, удовлетворяющие определенным условиям.

Можно сказать, что это «горизонтальное» подмножество начального отношения.

На языке SQL:R₁ WHERE xθy (θ (тэта) – любой оператор сравнения: <,>,=,…)

Например, из отношения Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы) вывести данные о тех, кто учится в группе ИНФ-31.

6) Проекция. Результатом проекции, примененной к отношению R₁, является отношение R₂, содержащее все кортежи R₁ после исключения из него некоторых атрибутов. Такие кортежи называются подкортежами.

Можно сказать, что это «вертикальное» подмножество начального отношения.

Специального оператора на SQL для проекции нет, т.к. для ее выполнения достаточно в стандартной конструкции запроса SELECT указать, какие атрибуты отношения берутся.

Обратим внимание на частные случаи:

·возможно указание списка всех атрибутов исходного отношения - это тождественная проекция;

·возможно указание пустого списка атрибутов – это нулевая проекция.

Например, из отношения Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, ДатаРождения, Адрес, Телефон, Группа) вывести для всех студентов информацию только о фамилии, имени, отчестве и группе.

7) Соединение. Результатом соединения отношений R₁ и R₂ является отношениеR₃, кортежи которого – это сцепление двух кортежей (принадлежащих соответственно R₁ и R₂), имеющих общее значение для одного или нескольких общих атрибутов R₁ и R₂.

Общий случай						Частный случай
R1			R2			R1			R2
a	x		x	l		a	x		x	l
b	y		y	m		b	y		y	m
c	z		z	n		c	z		y	n
		R3						R3
	a	x	l				a	x	l
	b	y	m				b	y	m
	c	z	n				b	y	n

Причем эти общие значения в результирующем отношении появляются только один раз.

На языке SQL:R₁ JOIN R₂

Соединение обладает свойствами:

• ассоциативность: (R₁ JOIN R₂) JOIN R₃=R₁ JOIN (R₂ JOIN R₃);
• коммутативность: (R₁ JOIN R₂) JOIN R₃=R₁ JOIN R₂ JOIN R₃.

Эта операция имеет несколько разновидностей, но самое распространенное – естественное соединение (на схеме). Есть еще θ(тэта)-соединение. Оно предназначено для случаев, когда два отношения соединяются на основе некоторых условий (xθy), отличных от эквивалентности.

В этом случае на SQL: (R₁ TIMES R₂) WHERE xθy,т.е. сочетание произведения и выборки.

Пример естественного соединения: соединение отношений Студенты и Группы по атрибуту Группа. В результате получится отношения, содержащую информацию о студентах и для каждого студента – о его группе.

Пример θ-соединения: соединение отношений Студенты и Группы по атрибуту Группа так, чтобы получить информацию о студентах только групп 5 курса.

8) Деление. Дадим определение для частного случая: для отношений R₁ (бинарного) и R₂ (унарного) результатом деления является отношение R₃, содержащее все значения одного

R1			R2
a	x		x
a	y		y
a	z
b	x		R3
c	y		a

9) атрибута R₁, которые соответствуют в другом атрибуте всем значениям R₂. Для отношений с большим количеством атрибутов – аналогично.

НаязыкеSQL: R₁ DIVIDEBY R₂

Например, в БД Факультет есть отношение Занятия (Группа, Дисциплина, Преподаватель). Чтобы получить список групп, которые изучают заданный набор дисциплин можно применить деление этого отношения на специально созданное унарное отношение, содержащее заданный набор дисциплин.

2.3.3. Дополнительные операторы реляционной алгебры

К восьми основным операторам реляционной алгебры были добавлены некоторые другие в качестве дополнительных. Их удобно использовать для практических целей, хотя можно реализовать через основные. Наиболее удачно основной набор дополнили две операции: расширение и подведение итогов.

Операция расширения

С ее помощью из исходного отношения создается новое, содержащий дополнительный атрибут, значения которого получены посредством некоторых скалярных вычислений.

EXTEND <имя отношения> ADD (<скалярное выражение>) AS< имя нового атрибута>

Примеры:

1)  Пусть есть отношение Преподаватели (КодПреподавателя, Фамилия, Имя, Отчество, ДатаПринятия). Для каждого преподавателя вывести стаж работы.

EXTEND Преподаватели ADD (year(date())-year(ДатаПринятия)) AS Стаж

2)  Частный случай - добавление нового атрибута, заполненного одинаковыми значениями: в отношение СекцииКружки базы данных Факультет добавить атрибут МестоПроведения, заполнив его одинаковыми значениями для всех секций – «ВятГГУ».

EXTEND СекцииКружки ADD («ВятГГУ») AS МестоПроведения

3)  Частный случай - переименование атрибута Адрес отношения Студенты в АдресРегистрации.

EXTEND Студенты ADD (Адрес) AS АдресРегистрации

Операция подведения итогов

Можно сказать, что если операция расширения обеспечивает возможность «горизонтального» вычисления, то операция подведения итогов обеспечивает возможность «вертикального» вычисления, т.е. дает возможность выполнить групповые операции по атрибутам (посчитать количество, сумму записей и т.п.)

SUMMARIZE <имя отношения> BY (<список имен атрибутов>)

ADD< групповая операция> AS <имя поля для итогового значения>

Групповыми операциями могут быть:

sum (<имя атрибута>) – сумма числовых значений;

count (<имя атрибута>) – количество значений;

min (<имя атрибута>) – минимальное значение;

max (<имя атрибута>) – максимальное значение.

Примеры:

1) Имеется отношение Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы) Подсчитать количество студентов в каждой группе.

SUMMARIZE Студенты BY (КодГруппы) ADD count(№ЗачетнойКнижки)

AS КоличествоСтудентов

2)  Имеется отношение Занятия (КодГруппы, Дисциплина, Преподаватель). Подсчитать количество групп, которые изучают более 10 дисциплин.

(SUMMARIZE Занятия BY (КодГруппы) ADD count(Дисциплина) AS N) WHERE N>10

2.3.4. Операции обновления

К операциям обновления относятся операции вставки, изменения и удаления.

Вставка: INSERT (<реляционное выражение или список атрибутов>) INTO <имя отношения>

Примеры:

1) Вставить новую запись в отношение Студенты.

INSERT (№зачетки=123456; Фамилия=«Иванов»; Имя=«Иван») INTO Студенты

2) В отношение Студенты31группы вставить те записи из отношения Студенты, которыесоответствуют студентам группы ИНФ-31.

INSERT (Студенты WHERE КодГруппы = «ИНФ-31») INTO Студенты31группы

Изменение: UPDATE <имя отношения> <реляционное выражение>

Пример: В отношении Студенты изменить группы «ИНФ-31» на «ИНФ-41».

UPDATE Студенты WHERE КодГруппы=«ИНФ-31» КодГруппы:=«ИНФ-41»

Удаление: DELETE< реляционное выражение>

Пример: Из отношения Студенты удалить всех студентов группы ИНФ-51.

DELETE Студенты WHERE КодГруппы=«ИНФ-51»

2.3.5. Значение реляционной алгебры

Основная цель реляционной алгебры – обеспечить запись выражений. А реляционные выражения не ограничиваются запросами.

В качестве примеров можно привести такие применения выражений:

• определение области выборки (WHERE…);
• определение области обновления (т.е. данных для вставки, изменения или удаления);
• определение правил целостности;
• определение правил безопасности (т.е. данных, для которых осуществляется контроль доступа).

То есть, можно сказать, что выражения обозначают символическую запись намерений пользователя БД, и эта символическая запись существует на языке SQL.

Язык называют реляционно полным, если его возможности соответствуют возможностям реляционных алгебраических операций.

3. Проектирование реляционных БД

3.1. Функциональные зависимости

Проектирование связано с построением логической структуры БД. Иными словами, нужно решить вопрос, какие базовые отношения, с какими атрибутами следует задать.

Суть этой проблемы сводится, в конечном счете, к нормализации отношений.

Сначала рассмотрим основные понятия, необходимые для обсуждения вопросов нормализации отношений.

3.1.1. Понятие функциональной зависимости

Вспомним, что любое отношение рассматривается как переменная, принимающая определенные значения в определенные моменты времени.

Обозначается: X→Y

Говорится: «X функционально определяет Y» или «Y функционально зависит от X».

Левая часть выражения называется детерминантом (детерминантой) функциональной зависимости (ФЗ), правая – зависимой частью ФЗ.

Например, в отношении Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, Адрес, КодГруппы) существуют такие ФЗ

{№ ЗачетнойКнижки} → {Фамилия, Имя, Отчество}

{№ ЗачетнойКнижки} → {Адрес, КодГруппы}

{№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес, КодГруппы}

Это лишь некоторые ФЗ, из которых можно сделать вывод, что если детерминант содержит первичный ключ, то множество всех остальных атрибутов отношения функционально зависит от него.

Еще пример: в отношении Кафедры (КодКафедры, НазваниеКафедры, Кабинет, Телефон) существуют ФЗ

{КодКафедры} → {Кабинет, Телефон}

{НазваниеКафедры} → {Кабинет, Телефон}

Таким образом, аналогичный вывод можно сделать не только для первичных ключей, но и для альтернативных, то есть для всех потенциальных ключей.

Рассмотрим еще один пример: если в то же отношение Студенты добавить атрибут СтаростаГруппы, то появятся такие ФЗ:

{КодГруппы} → {СтаростаГруппы}

{СтаростаГруппы} → {КодГруппы}

(причем, ни атрибут КодГруппы, ни атрибут СтаростаГруппы не являются потенциальными ключами)

В этом случае имеется избыточность данных, которая может привести к вводу ошибочных сведений (пользователь случайно может ввести в качестве старосты некоторой группы не того студента, который на самом деле является старостой, но система не выдаст ошибку).

Фактически, если в отношении имеется ФЗ, в которой детерминант не является суперключом, то отношение избыточно.

Существуют такие ФЗ, которые учитываются только формально, т.к. они всегда существуют и подразумеваются самим определением ФЗ. Это тривиальные ФЗ.

Например,

{№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Фамилия, Имя, Отчество}

{КодГруппы, Курс} → {Курс}

Такие тривиальные ФЗ не рассматриваются при нормализации, но все же они существуют и всегда формально учитываются.

3.1.2. Правила вывода функциональных зависимостей

Из некоторого множества ФЗ конкретного отношения можно получить производные ФЗ.

Например, из ФЗ отношения Студенты

{№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес, Телефон}

можно получить такие ФЗ:

{№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес}

{№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Телефон}

Чтобы получить замыкание некоторого множества ФЗ нужны правила вывода ФЗ. Такие правила вывода сформулировал Армстронг (Швеция), поэтому их называют правилами Армстронга (или аксиомами Армстронга).

Обозначим за А, В, С произвольные подмножества множества атрибутов заданного отношения R, а записью АВ будем обозначать объединение А и В.

Каждое из этих правил может быть доказано на основе определения ФЗ, а первое правило – это определение тривиальной ФЗ.

Эти правила полны, т.к. их достаточно для вывода замыкания (т.е. всех ФЗ) начального множества ФЗ.

Они также исчерпывающи, т.к. никакие дополнительные ФЗ не могут быть выведены из начального множества ФЗ.

Но из этих правил для упрощения практического вывода ФЗ можно вывести несколько дополнительных правил (следствий):

4) Самоопределение: А → А

5) Декомпозиция: если А → ВС, то А → В и А → С

6) Объединение: если А → В и А → С, то А → ВС

7) Композиция: если А → В и С → D, то АС → ВD

8) Теорема всеобщего объединения: если А → В и С → D, то А(С-В) → ВD

(названо это правило так, потому что многие другие правила могут быть выведены как частные случаи этой теоремы)

Пример: рассмотрим отношение Группы (КодГруппы, Специальность, Курс,Староста).

В качестве начального множества ФЗ возьмем множество из следующих двух ФЗ:

(1) {КодГруппы} → {Специальность, Курс}

(2) {КодГруппы} → {Староста}

Выведем замыкание этого множества ФЗ.

·По правилу 1 можно записать все тривиальные зависимости:

(3) {Специальность, Курс} → {Специальность}

(4) {Специальность, Курс} → {Курс}

·По правилу 2:

(5) {КодГруппы, Староста} → {Специальность, Курс, Староста}

(6) {КодГруппы, Специальность} → {Староста, Специальность}

(7) {КодГруппы, Курс} → {Староста, Курс}

(8) {КодГруппы, Специальность, Курс} → {Староста, Специальность, Курс}

·По правилу 3 напрямую ничего не выведем.

·По правилу 4:

(9) {КодГруппы} → {КодГруппы}

(10) {Специальность} → {Специальность}

и т.д. (11), (12)

·По правилу 5:

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

·По правилу 6:

(15) {КодГруппы} → {Специальность, Курс, Староста}

·По правилу 7 напрямую ничего не выведем

·По правилу 8 тоже.

Однако, знание этих правил и умение ими пользоваться не обеспечивают вывода замыкания множества ФЗ, т.к. не существует четкого алгоритма такого вывода.

3.1.3. Неприводимые функциональные зависимости

Например: ФЗ {№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес} приводима, т.к. из детерминанта можно исключить атрибуты Фамилия, Имя, Отчество без нарушения ФЗ.

А ФЗ {КодГруппы, Дисциплина} → {Преподаватель} отношения Занятия (КодГруппы, Дисциплина, Преподаватель) неприводима, т.к. из детерминанта нельзя исключить ни атрибут КодГруппы, ни атрибут Дисциплина без нарушения зависимости.

Например, рассмотрим множество ФЗ отношения Группы из примера в предыдущем п.3.1.2.

(1) {КодГруппы} → {Специальность, Курс}

(2) {КодГруппы} → {Староста}

(3) {Специальность, Курс} → {Специальность}

(4) {Специальность, Курс} → {Курс}

(5) {КодГруппы, Староста} → {Специальность, Курс, Староста}

(6) {КодГруппы, Специальность} → {Староста, Специальность}

(7) {КодГруппы, Курс} → {Староста, Курс}

(8) {КодГруппы, Специальность, Курс} → {Староста, Специальность, Курс}

(9) {КодГруппы} → {КодГруппы}

(10) {Специальность} → {Специальность}

(11) {Курс} → {Курс}

(12) {Староста} → {Староста}

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

(15) {КодГруппы} → {Специальность, Курс, Староста}

По первому свойству исключаем из этого множества следующие ФЗ: (1), (5), (6), (7), (8), (15).

По второму свойству исключаем следующие ФЗ: (3), (4).

По третьему свойству исключаем: (9), (10), (11), (12).

Остались:

(2) {КодГруппы} → {Староста}

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

Полученное множество ФЗ неприводимо. Можно сделать вывод, что полученное множество ФЗ выражает то, что отношение Группы содержит атрибуты КодГруппы, Староста, Специальность, Курс, и КодГруппы – первичный ключ.

3.1.4. Диаграммы (схемы) функциональных зависимостей

Множество неприводимых ФЗ некоторого отношения можно представить в виде диаграммы функциональных зависимостей.

Из таких диаграмм лучше видно, какие ФЗ включить в множество ФЗ, а какие исключить, чтобы оно было неприводимо. Исключить нужно те стрелки (обозначающие ФЗ), которые идут не от потенциального ключа.

Таким образом, с помощью диаграмм можно привести множество ФЗ к неприводимому состоянию.

В качестве примера рассмотрим диаграмму первоначального множества ФЗ из п. 3.1.2.

После того, как лишние стрелки будут убраны, получим диаграмму:

Из нее как раз и следуют перечисленные ранее три оставшиеся ФЗ:

{КодГруппы} → {Курс}

{КодГруппы} → {Специальность}

{КодГруппы} → {Староста}

Таким образом, существует как минимум два способа преобразования множества ФЗ к неприводимому состоянию - путем проверки всех свойств их определения и путем анализа диаграмм ФЗ.

3.2. Нормализация отношений

Вся теория нормализации отношений является не более и не менее как формализацией соображений здравого смысла. Потребность такой формализации в том, чтобы сформулировать общие правила для разработчиков БД, а главное – если такая задача будет полностью выполнена - эти правила могут быть автоматизированы для реализации на ЭВМ.

3.2.1. Обзор нормальных форм

Процесс нормализации отношений основан на концепции нормальных форм (НФ).

Говорят, что отношение находится в некоторой НФ, если оно удовлетворяет заданному набору условий.

Известно несколько НФ (рис. 4).

Из рис. 4 видно, что все условия, необходимые для некоторой НФ, должны выполняться и для всех последующих НФ.

Первые три НФ были определены Коддом, следующая – нормальная форма Бойса-Кодда (НФБК) – Бойсом и Коддом, 4 и 5 НФ были определены Фейгином.

Возникает вопрос, можно ли продолжить нормализацию дальше, получить 6, 7 и т.д. НФ? Действительно, существуют дополнительные НФ, но 5 НФ считается в некотором смысле окончательной. А для практического проектирования достаточной считают 3 НФ.

3.2.2. Декомпозиция без потерь

Нормализация использует операцию декомпозиции. Дело в том, что процедура нормализации предусматривает разбиение отношения на другие, т.е. его декомпозицию. Причем эта декомпозиция должна произойти без потерь информации из первоначального отношения. Можно сказать, что декомпозиция должна быть обратимой.

Например, рассмотрим отношение Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы, Адрес, Телефон).

Выполним декомпозицию на два отношения:

Студенты1 (№ЗачетнойКнижки, Фамилия, Имя, Отчество) и

Студенты2 (КодГруппы, Адрес, Телефон)

При такой декомпозиции информация утрачивается – для каждой группы будет выведены адрес и телефон только первого по списку студента этой группы. При соединении полученных отношений невозможно восстановить полностью первоначальное отношение.

Выполним декомпозицию по-другому:

Студенты3 (№ЗачетнойКнижки, Фамилия, Имя, Отчество) и

Студенты4 (№ЗачетнойКнижки, Адрес, Телефон)

Вот это – декомпозиция без потерь. Можно соединить полученные два отношения, получив первоначальное.

По своей сути декомпозиция – это операция проекции реляционной алгебры, поэтому каждое полученное при декомпозиции отношение называют проекциями первоначального.

Возникает вопрос: какие условия должны соблюдаться для того, чтобы проекции первоначального отношения при обратном соединении гарантировали получение исходного отношения? На этот вопрос дает ответ теорема Хеза:

(Заметим, что теорема не утверждает «тогда и только тогда»).

3.2.3. Первая, вторая и третья нормальные формы

Иными словами:

Например, если в отношении есть поле ФИО, отношение не находится в 1 НФ, т.к. значения этого поля можно разделить на фамилию, имя и отчество.

Например, рассмотрим отношение Успеваемость (№ЗачетнойКнижки, Фамилия, Имя, Отчество, Дисциплина, Оценка).

Если первичным ключом здесь назначить №ЗачетнойКнижки, то от этого ключа не будет зависеть атрибут Дисциплина. Т.е. в этом случае отношение не находится во 2 НФ.

Можно тогда в качестве первичного ключа взять множество атрибутов {№ЗачетнойКнижки, Дисциплина}. В этом случае от такого ключа зависят все атрибуты, но атрибуты Фамилия, Имя, Отчество зависят приводимо, т.к. из детерминанта следующей ФЗ можно убрать атрибут Дисциплина без нарушения зависимости:

{№ЗачетнойКнижки, Дисциплина} → {Фамилия, Имя, Отчество}

И при таком первичном ключе отношение не находится во 2 НФ.

Чтобы получить отношения во 2 НФ произведем декомпозицию. Можно это сделать по теореме Хеза.

Отношение Успеваемость удовлетворяет ФЗ:

{№ЗачетнойКнижки} → {Фамилия, Имя, Отчество} (А → В)

Вне этой ФЗ осталось следующее множество атрибутов: {Дисциплина, Оценка} (С)

Тогда по теореме Хеза отношение Успеваемость равно соединению его проекций с такими множествами атрибутов:

{№ЗачетнойКнижки, Фамилия, Имя, Отчество} ({А, В})

{№ЗачетнойКнижки, Дисциплина, Оценка} ({А, С})

То есть, декомпозиция без потерь возможна на отношения:

Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество)

Успеваемость1 (№ЗачетнойКнижки, Дисциплина, Оценка).

Иными словами:

Например, добавим в отношение Студенты атрибут СтаростаГруппы. Тогда в отношении будут следующие ФЗ:

{№ЗачетнойКнижки} → {КодГруппы}, {КодГруппы} → {СтаростаГруппы}

То есть атрибут СтаростаГруппы зависит от первичного ключа (№ЗачетнойКнижки) транзитивно через атрибут КодГруппы, а не напрямую.

Значит, это отношение не находится в 3 НФ.

Проведем декомпозицию. В данном случае по теорема Хеза может быть два варианта декомпозиции.

1 вариант основан на ФЗ {№ЗачетнойКнижки}→{Фамилия, Имя, Отчество, КодГруппы}.

В результате получим такие проекции:

{№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы} и

{№ЗачетнойКнижки, СтаростаГруппы}

2 вариант основан на ФЗ {КодГруппы}→{СтаростаГруппы}.

В результате получим такие проекции:

{КодГруппы, СтаростаГруппы}

{КодГруппы, №ЗачентойКнижки, Фамилия, Имя, Отчество}

Подходит второй вариант, т.к. при первом варианте возможны ошибки при обновлении данных (пользователь может ввести для конкретного студента старосту неверно, и система не выдаст ошибки). Такая ситуация говорит о том, что теорема Хеза не всегда является удачным и единственным способом для выбора проекций при декомпозиции.

В результате при декомпозиции на две проекции

Группы (КодГруппы, СтаростаГруппы) и

Студенты1 (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы)

получим отношения в 3 НФ.

Таким образом, если отношение не находится ни во 2 НФ, ни в 3 НФ, существует избыточность, которая приводит к так называемым аномалиям обновления, т.е. нарушении целостности при вставке, удалении или изменении данных.

Например, рассмотрим отношение, которое не находится ни во 2 НФ, ни в 3 НФ.

Успеваемость (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы, СтаростаГруппы, Дисциплина, Оценка).

Изобразим диаграмму ФЗ этого отношения:

Какие могут произойти аномалии при обновлении данных в таком отношении?

Например, такие:

• При добавлении нового студента при правильном указании группы, в которой он учится, может быть ошибочно указан староста группы.
• При удалении одной из записей будет удалена не только информация об оценке соответствующего студента, но и информация о том, в какой группе он учится.
• При изменении старосты группы необходимо вручную изменить его для всех записей студентов этой группы – при этом можно ошибиться.

Для этого отношения можно произвести декомпозицию. Это удобно сделать, руководствуясь схемой. Например, на три следующие проекции:

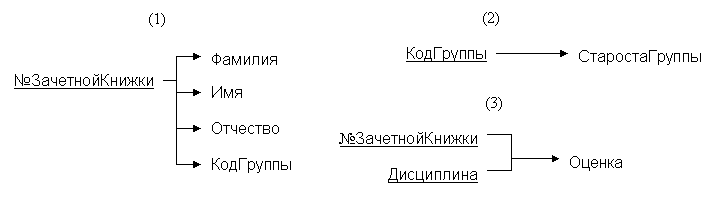
Все полученные отношения находятся во2 НФ и в 3 НФ.

Но без потерь ли произведена эта декомпозиция? Да, т.к. после соединения этих трех отношений получим первоначальное.

Полученные отношения являются независимыми проекциями.

Для наших трех проекций первое условие выполняется, т.к. все их ФЗ (обозначенные стрелками) обеспечивают ФЗ первоначального отношения.

Выполняется и второе условие: для проекций (1) и (2) общий атрибут – КодГруппы, он первичный ключ для (2); для (1) и (3) общий атрибут - №ЗачетнойКнижки, он первичный ключ для (1).

А вот если разбить отношение Успеваемость на следующие проекции:

(4)

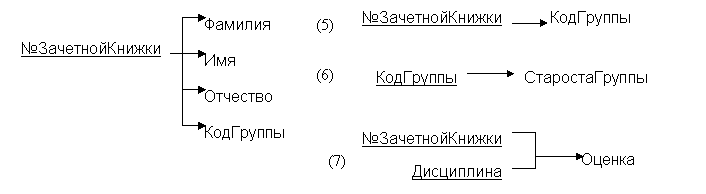
первое условие выполнится, а второе - не выполнится (атрибут КодГруппы общий для (4) и (5), но не является потенциальным ключом ни в одном из них). То есть, эти проекции не являются независимыми.

Но это не означает, что любое неатомарное отношение может быть разбито на атомарные отношения. И не всегда есть смысл такого разбиения.

Например, отношение Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы) атомарно. А отношение Студенты1 (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы, Адрес, ДомашнийТелефон) неатомарно, т.к. домашний телефон зависит от адреса, поэтому отношение Студенты1 можно разбить на такие независимые проекции: Студенты2 (№ЗачетнойКнижки, Фамилия, Имя, Отчество, Адрес) и АдресаТелефоны (Адрес, ДомашнийТелефон). Но в этом нет смысла.

3.2.4. Нормальная форма Бойса-Кодда

При определении 3 НФ делалось допущение о том, что отношение имеет только один потенциальный ключ, который и является первичным. Но определение 3 НФ не совсем подходит для отношений со следующими свойствами:

1. отношение имеет два или более потенциальных ключа;
2. потенциальные ключи сложные;
3. потенциальные ключи перекрываются, т.е имеют хотя бы один общий атрибут.

Для отношений, обладающих этими свойствами данного ранее определения 3 НФ недостаточно, поэтому Бойс и Кодд ввели определение НФ Бойса-Кодда.

На практике отношения с комбинацией перечисленных свойств встречаются крайне редко, а для отношений без этих свойств 3 НФ и НФБК эквивалентны.

Можно заметить, что определение НФБК проще, чем 3 НФ, т.к. в нем нет упоминания 2 НФ и не используется понятие транзитивной зависимости.

Например, рассмотрим отношение с двумя перекрывающимися потенциальными ключами.

Успеваемость (№ЗачетнойКнижки, КодДисциплины, НазваниеДисциплины, Оценка)

Потенциальные ключи: {№ЗачетнойКнижки, КодДисциплины} и {№ЗачетнойКнижки, НазваниеДисциплины}.

Это отношение не в НФБК, т.к. в нем есть такие ФЗ:

КодДисциплины → НазваниеДисциплины

НазваниеДисциплины → КодДисциплины

А детерминанты этих ФЗ не являются потенциальными ключами.

Это отношение также не в 3 НФ, т.к. не находится во 2 НФ, потому что атрибут НазваниеДисциплины зависит только от части первичного ключа (ФЗ {№ЗачетнойКнижки, КодДисциплины} → {НазваниеДисциплины} приводима).

Видно, что этому отношению присуща избыточность.

Возможна декомпозиция на два отношения:

Дисциплина (КодДисциплины, НазваниеДисциплины)

Успеваемость1 (№ЗачетнойКнижки, КодДисциплины, Оценка)

Рассмотрим пример отношения, которое находится в 3 НФ, но не находится в НФБК. Пусть в БД Факультет есть отношение Занятия (КодГруппы, Дисциплина, Преподаватель):

КодГруппы	Дисциплина	Преподаватель
ИНФ-21	ПО ЭВМ	Пятышева Е.А.
ИНФ-22	ПО ЭВМ	Суворова Т.Н.
ИНФ-31	СУБД	Шиляева М.С.
ИНФ-32	СУБД	Петухова М.В.
…

Введем следующие ограничения:

a) каждую дисциплину у конкретной группы ведет только один преподаватель, но одну и ту же дисциплину могут вести разные преподаватели;

b) каждый преподаватель ведет только одну дисциплину (в действительности это не всегда так, но мы предположим именно это).

Тогда существует два потенциальных ключа: {КодГруппы, Дисциплина} и {КодГруппы, Преподаватель}. Опять ситуация с двумя перекрывающимися потенциальными ключами. Первый из них назначим первичным.

Это отношение в 3 НФ, т.к.

1. Оно находится во 2 НФ. Докажем это: единственная ФЗ неключевого атрибута {КодГруппы, Дисциплина} → Преподаватель. Она неприводима, т.к. атрибут КодГруппы из детерминанты исключить нельзя (одну и ту же дисциплину могут вести разные преподаватели, т.е. не верна ФЗ Дисциплина → Преподаватель); атрибут Дисциплина тоже исключить нельзя (группа изучает несколько дисциплин у разных преподавателей, т.е. не верна ФЗ КодГруппы → Преподаватель).
2. Отношение находится и в 3 НФ. Докажем это: в единственной ФЗ для неключекого атрибута (см. 1) этот неключевой атрибут нетранзитивно зависит от первичного ключа.

Но это отношение не в НФБК, т.к. есть ФЗ Преподаватели → Дисциплины (по условию каждый преподаватель может вести только одну дисциплину), и детерминант этой ФЗ не является потенциальным ключом.

Поэтому в отношении Занятия могут произойти аномалии обновления. Например, если требуется удалить информацию о группе ИНФ-31, то при этом утратится информация о том, что дисциплину СУБД ведет преподаватель Шиляева М.С.

Необходима декомпозиция на проекции, которые будут в НФБК:

ГП (Группа, Преподаватель) и ПД (Преподаватель, Дисциплина)

Но эти проекции не являются независимыми, т.к. при попытке вставить новую запись в одну из них может возникнуть противоречие. Например, вставляем в отношение ГП кортеж {ИНФ-31, Васенина Е.А.}, но если, допустим, Васенина Е.А. преподает дисциплину ИТО, и в этом отношении есть уже кортеж {ИНФ-31, Огородников Е.В.} и преподаватель Огородников Е.В. тоже преподает дисциплину ИТО. Возникнет противоречие (два преподавателя ведут одну дисциплину у одной группы). А проверить это можно только в отношении ПД.

Вывод: не всегда можно достичь две цели сразу – разбить на отношения в НФБК и чтобы эти отношения были независимы.

Действительно, отношение Занятия является атомарным, но атомарность не является ни необходимым, ни достаточным условие хорошего макета БД. А если стремиться к НФБК, то это в некоторых случаях усложняет БД.

Все это показывает, что на практике целей лучше избегать отношений с перекрывающимися потенциальными ключами, тогда достаточно 3 НФ.

Но если без них сложно обойтись, то вводят особые правила обновления, в каждом конкретном случае – свои.

3.3. Нормальные формы более высокого порядка

3.3.1. Многозначные зависимости

Для введения 4 НФ необходимо ввести понятие многозначной зависимости (МЗ).

Обозначается: А 8 В

Говорится: «А многозначно определяет В» или «В многозначно зависит от А» или «А двойная стрелка В».

Упрощенно можно сказать так: А многозначно определяет В, если для каждого значения А не существует единственного соответствующего ей значения В (не верна ФЗ А ® В), но каждое значение А определяет множество соответствующих ей значений В.

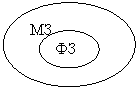По сути ФЗ – это частный случай МЗ:

Пример, который пояснит суть МЗ:

Пусть имеется отношение ДПК (Дисциплина, Преподаватель, Кабинет).

Дисциплина	Преподаватель	Кабинет
ИС	Огородников Е.В.	140
ИС	Огородников Е.В.	218
ИС	Шиляева М.С.	140
ИС	Шиляева М.С.	218
СУБД	Шиляева М.С.	315
СУБД	Шиляева М.С.	411
СУБД	Петухова М.В.	315
СУБД	Петухова М.В.	411
…

Введем следующие ограничения:

a) каждой дисциплине может соответствовать любое количество преподавателей и любое количество кабинетов;

b) преподаватели и кабинеты не зависят друг от друга (т.е. независимо от того, кто преподает данную дисциплину, для этой дисциплины используется один и тот же набор кабинетов);

c) конкретный преподаватель и конкретный кабинет могут быть связаны с любым количеством дисциплин.

В этом случае первичный ключ – множество всех атрибутов.

Проверим, в каких НФ находится это отношение.

1) 1 НФ – т.к. атрибуты неделимы (будем считать, что вместо ФИО преподавателя используется некий код преподавателя, но для удобства в примере будем использовать ФИО).

2) 2 НФ – т.к. неключевых атрибутов вообще нет.

3) 3 НФ – по той же причине.

4) НФБК – не подходит для этого отношения, т.к. в нем нет нескольких перекрывающихся потенциальных ключей.

Попутно можно сделать вывод, что полностью ключевое отношение (если оно в 1 НФ) находится в 3 НФ и в НФБК.

По ограничению b) можно утверждать, что если существуют два кортежа

{Дисциплина1, Преподаватель1, Кабинет1} и

{Дисциплина1, Преподаватель2, Кабинет2},

то существуют и кортежи

{Дисциплина1, Преподаватель1, Кабинет2} и

{Дисциплина1, Преподаватель2, Кабинет1}.

Например, если существуют кортежи

{СУБД, Шиляева М.С., 315} и

{СУБД, Петухова М.В., 411},

то существуют и кортежи

{СУБД, Шиляева М.С., 411} и

{СУБД, Петухова М.В., 315}.

В этом случае отношение явно избыточно и может привести к аномалиям обновления. Например, для добавления информации о том, что дисциплина СУБД будет вестись новым преподавателем Ивановым И.И. необходимо создать столько новых кортежей, сколько кабинетов подходят для этой дисциплины. А при этом ошибочно можно ввести кортежи не для всех кабинетов или, наоборот, с лишними кабинетами.

Существование подобных проблем вызвано, как правило, независимостью атрибутов. В нашем примере – атрибутов Преподаватель и Кабинет.

Как исправить ситуацию, чтобы избежать избыточности и аномалий обновления?

Можно заменить отношение ДПК двумя его проекциями:

ДП (Дисциплина, Преподаватель) и ДК (Дисциплина, Кабинет)

Обе проекции полностью ключевые, следовательно, находятся в НФБК.

Кроме того, это декомпозиция без потерь, т.к. при соединении обратно по атрибуту Дисциплина получим первоначальное отношение ДПК.

Можно сказать, что все эти рассуждения были на интуитивном уровне, из соображений здравого смысла – мы не пользовались какими-либо строгими правилами.

Только в 1971 году эти соображения были формализованы Фейгином с помощью понятия многозначных зависимостей.

Формализуем процесс декомпозиции отношения ДПК. Этого нельзя сделать, основываясь на ФЗ, т.к. диаграмма ФЗ выглядит так:

 

 

И все ФЗ здесь тривиальны.

Но произведенную декомпозицию можно сделать на основе МЗ, т.к. в отношении их две:

Дисциплина 8 Преподаватель

Дисциплина 8 Кабинет

Первая означает, что хотя для каждой дисциплины не существует единственного соответствующего ей преподавателя (не верна ФЗ Дисциплина ® Преподаватель), но каждая дисциплина определяет множество соответствующих ей преподавателей.

Вторая означает, что хотя для каждой дисциплины не существует единственного соответствующего ей кабинета (не верна ФЗ Дисциплина ® Кабинет), но каждая дисциплина определяет множество соответствующих ей кабинетов.

По этим МЗ и можно произвести декомпозицию.

Можно заметить, что для отношения ДПК многозначная зависимость Дисциплина 8 Преподаватель выполняется тогда и только тогда, когда выполняется МЗ Дисциплина 8 Кабинет.

Для подобных отношений это выполняется всегда, т.е. в обобщенном виде можно сформулировать правило многозначных зависимостей:

Таким образом, МЗ образуют пары и их обычно представляют так: А 8В½С.

Для ДПК можно записать Дисциплины 8 Преподаватели½Кабинеты.

Теорема Фейгина:

3.3.2. Четвертая нормальная форма

Другая формулировка:

Отношение ДПК из предыдущего примера не находится в 4 НФ, т.к. (по первой формулировке):

1) Существует МЗ Дисциплина 8 Преподаватель, но при этом атрибут Кабинет не зависит функционально от атрибута Дисциплина.

2) Существует МЗ Дисциплина 8 Кабинет, но при этом атрибут Преподаватель не зависит функционально от атрибута Дисциплина.

Но обе проекции ДП и ДК находятся в 4 НФ, т.к. в каждой из них существует по одной МЗ, и других атрибутов (не входящих в эти МЗ) нет.

Фейгин доказал также, что 4 НФ всегда может быть получена, т.е. любое отношение, содержащее МЗ может быть подвергнуто декомпозиции без потерь на набор отношений в 4 НФ.

3.3.3. Зависимость соединения

Не всегда можно произвести декомпозицию без потерь одного отношения на две проекции. Если это невозможно, но возможно разбить отношение на три или более проекций, такое отношение называют n-декомпозируемым, где n – число проекций, на которое можно разбить отношение без потерь.

Например, рассмотрим отношение ЛДС (Литература, Дисциплина, Специальность), полностью ключевое. Это отношение выражает информацию о том, что некая имеющаяся в библиотеке книга подходит для некоторой дисциплины, изучаемой определенной специальностью.

Отношение ЛДС:

Литература	Дисциплина	Специальность
Хомоненко А. и др. Базы данных	СУБД	Информатика с доп. спец. ин. язык
Хомоненко А. и др. Базы данных	ИС	Математика с доп. спец. информатика
Хомоненко А. и др. Базы данных	ИС	Информатика с доп. спец. ин. язык
Дейт К. Введение в системы баз данных	СУБД	Информатика с доп. спец. ин. язык
Дейт К. Введение в системы баз данных	ИС	Информатика с доп. спец. ин. язык

Произведем декомпозицию на три проекции: ЛД, ДС, ЛС.

ЛД ДС ЛС

Литература	Дисциплина		Дисциплина	Специальность		Литература	Специальность
Хомоненко	СУБД		СУБД	Информатика		Хомоненко	Информатика
Хомоненко	ИС		ИС	Математика		Хомоненко	Математика
Дейт	СУБД		ИС	Информатика		Дейт	Информатика
Дейт	ИС

Соединим обратно только две проекции, ЛД и ДС по атрибуту Дисциплина, и сравним кортежи полученного отношения с кортежами первоначального отношения ЛДС:

Литература	Дисциплина	Специальность
Хомоненко	СУБД	Информатика	- есть
Хомоненко	ИС	Математика	- есть
Хомоненко	ИС	Информатика	- есть
Дейт	СУБД	Информатика	- есть
Дейт	ИС	Математика	- нет!
Дейт	ИС	Информатика	- есть

В результате получили лишний кортеж.

Аналогичная ситуация будет и при соединении ЛД и ЛС, а также ДС и ЛС.

А если соединить все три проекции, то получим именно первоначальное отношение ЛДС.

Таким образом, можно сделать вывод, что отношение ЛДС 3-декомпозируемо.

В связи с такими n-декомпозициями вводится понятие зависимости соединения (ЗС), на основе которого затем определяется 5 НФ.

Для нашего примера отношение ЛДС удовлетворяет зависимости соединения

*(ЛД, ДС, ЛС) или

*({Литература,Дисциплина},{Дисциплина,Специальность},{Литература,Специальность}).

Как ФЗ является частным случаем МЗ, так и МЗ является частным случаем ЗС.

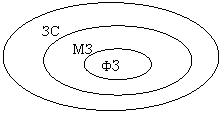3.3.4. Пятая нормальная форма

Например, рассмотрим отношение Группы (КодГруппы, НазваниеГруппы, Курс, Староста). Имеется два потенциальных ключа: КодГруппы и НазваниеГруппы. Эти ключи подразумевают (т.е. обеспечивают) такие, например, ЗС:

*({КодГруппы, Староста}, {КодГруппы, НазваниеГруппы, Курс})

*({КодГруппы, НазваниеГруппы}, {КодГруппы, Курс}, {НазваниеГруппы, Староста})

и т.п.

А если убрать альтернативный ключ (НазваниеГруппы), оставив единственный потенциальный ключ (КодГруппы), то еще проще:

*({КодГруппы, Курс}{КодГруппы, Староста})

и всё.

Рассмотренное в предыдущем примере отношение ЛДС не в 5 НФ, т.к. ЗС *(ЛД, ДС, ЛС) не подразумевается единственным в этом отношении потенциальным ключом {Литература, Дисциплина, Специальность}.

Найти все ЗС гораздо сложнее, чем ФЗ и МЗ, - нет точного алгоритма такого поиска. То есть процесс проверки отношения на 5 НФ не определен достаточно четко. Утешает то, что на практике подобные отношения встречаются редко.

Из определения 5 НФ можно сделать вывод, что эта НФ является окончательной по отношению к проекции и соединению (это и отражено в ее втором названии).

Таким образом, гарантируется, что отношение в 5 НФ не содержит избыточности данных, которые могут привести к аномалиям обновления.

3.4. Итоговая схема процедуры нормализации

В общем случае можно выделить следующие четыре цели процедуры нормализации:

1. Исключение избыточности.
2. Устранение аномалий обновления.
3. Проектирование макета данных, который соответствовал бы реальному миру, был интуитивно понятен и служил основой для дальнейшего развития.
4. Упрощение процесса наложения ограничений целостности. Эта цель связана с потенциальными ключами, т.е. если соблюдать условие уникальности потенциальных ключей и организовывать связи только через них, то эта цель будет достигнута.

Пусть имеется отношение R, которое находится в 1 НФ. Также известны все ограничения этого отношения, т.е. ключи, ФЗ, МЗ и ЗС.

Тогда основная идея нормализации отношения R состоит в декомпозиции без потерь, принципы которой в следующем:

·последовательно отношение R приводится к набору меньших отношений, который эквивалентен отношению R, но более предпочтителен;

·каждый этап этого процесса состоит из разбиения на проекции отношений, полученных на предыдущем этапе;

·при этом все заданные зависимости (ФЗ, МЗ, ЗС) используются на каждом шаге для выбора проекций следующего этапа.

Перечислим основные правила, на которые опирается процедура нормализации.

1. Отношение в 1 НФ следует разбить на проекции для исключения всех приводимых ФЗ. В результате – набор отношений во 2 НФ.
2. Отношения во 2 НФ следует разбить на проекции для исключения всех транзитивных ФЗ. В результате – набор отношений в 3 НФ.
3. Отношение в 3 НФ следует разбить на проекции для исключения всех оставшихся ФЗ, в которых детерминанты не являются потенциальными ключами. В результате – набор отношений в НФБК.
   (Заметим, что все первые три правила можно сконцентрировать в одном: «исходное отношение следует разбить на проекции для исключения всех ФЗ, в которых детерминанты не являются потенциальными ключами»)
4. Отношение в НФБК следует разбить на проекции для исключения всех МЗ, которые не являются ФЗ. В результате – набор отношений в 4 НФ. (На практике такие МЗ обычно исключаются перед первым этапом, т.е. отделяются независимые повторяющиеся группы)
5. Отношение в 4 НФ следует разбить на проекции для исключения всех ЗС, которые не подразумеваются потенциальными ключами (если такие ЗС можно выявить). В результате – набор отношений в 5 НФ.

К правилам можно выделить следующие дополнения:

1. Процесс разбиения на проекции должен быть выполнен без потерь и с сохранением зависимостей исходных данных.
2. При проверке на НФБК, 4 НФ и 5 НФ можно пользоваться их альтернативными определениями, что иногда бывает удобнее, - в зависимость от конкретной ситуации.
3. Бывают ситуации, когда удобнее менять последовательность процедуры нормализации.
4. Хотя идеи нормализации важны и наиболее приемлемы для проектирования БД, они не являются универсальным средством по следующим причинам:
   • кроме ФЗ, МЗ и ЗС существуют и другие типы зависимостей и ограничений – специфические для каждой БД;
   • декомпозиция может быть не уникальной, т.е. могут существовать разные ее варианты. А для выбора предпочтительного не так уж много критериев;
   • не всякую избыточность данных можно устранить разбиением на проекции.

Но, несмотря на эти замечания, можно сказать, что методика нисходящего проектирования БД, реализованная в нормализации отношений, позволяет создать непротиворечивый, нормализованный макет БД.