3.2.1. Принципы построения MIMO-системы связи

3.2.2. Пропускная способность MIMO – систем

3.2.3. Алгоритм BLAST - пространственного декодирования

3.2.4. Неадаптивная многоантенная техника с числом передающих антенн большим, чем число приемных (MIMO + STBC)

3.2.5. Адаптивная модуляция и адаптивное кодирование в многоантенных системах

В данном разделе рассматриваются многоантенные системы связи не с одним, а с несколькими пространственными каналами. В таких системах как в передатчике, так и в приемнике используются несколько антенн. Их часто называют системами с многими входами и многими выходами (MIMO – Multiple Input Multiple Output). В разд. 3.2.1, 3.2.2, 3.2.3 полагается, что число передающих антенн не больше числа приемных . В этом случае можно получить скорости передачи информации, близкие к предельным без адаптации, т. е. если параметры канала неизвестны в передатчике. Иной случай - рассматривается в разд. 3.2.4 и 3.3.

В разд. 3.2.1 приводится структура МIMO - системы связи, объясняются принципы ее функционирования и причины высокой спектральной эффективности. В разд. 3.2.2 приведены формулы для расчета пропускной способности и результаты моделирования для систем с различным числом передающих и приемных антенн. В разд. 3.2.3 описан разработанный лабораторией Bell-labs для многоантенной техники алгоритм BLAST (Bell laborotories Layered Space-Time). В разд. 3.2.4 приведен алгоритм, позволяющий применять МIMO технику без адаптации в передатчике при . В разд. 3.2.5 кратко описана процедура измерения характеристик радиоканала и связанные с ней проблемы.

3.2.1. Принципы построения MIMO-системы связи

Блок-схема MIMO-системы связи с передающими и приемными антеннами при приведена на рис. 3.3. На ней входной поток данных делится на подпотоков.

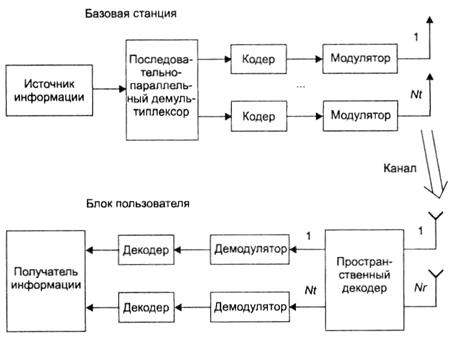
Рис. 3.3. Блок-схема MIMO-системы связи

Последовательно-параллельный демультиплексор на рис. 3.3 выполняет это разделение. Каждый подпоток после кодирования и модуляции излучается отдельной антенной. Причем все подпотоков излучаются одновременно в одной и той же полосе частот. Для всех подпотоков могут использоваться идентичные коды и модуляторы.

Излученные потоков создают сигналы в каждой из приемных антенн. То есть сигнал в каждой приемной антенне — это смесь излученных сигналов, умноженных на комплексные передаточные функции от соответствующих передающих антенн к рассматриваемой приемной антенне. Иначе говоря, вектор принятых сигналов представляет произведение матрицы канала на вектор излученных сигналов. Матрица канала измеряется перед передачей информации и считается известной в приемнике.

Далее в приемнике решается задача разделения и оценки излученных сигналов. Для этого нужно решить систему из уравнений с неизвестными. При можно воспользоваться матрицей, обратной матрице канала. При можно применить обобщенную инверсию, получающуюся при решении системы методом наименьших квадратов - MMSE (Minimum Mean – Square Error). На рис. 3.3 блок, выделяющий подпотоков из принятых сигналов, назван пространственным декодером. Далее каждый подпоток подается на демодулятор и декодер.

Организованная таким образом MIMO – система связи обеспечивает передачу информации по пространственным каналам. Причем все каналы работают в одной и той же полосе частот и разделяются только за счет пространственного разнесения излучающих и приемных антенн. Рассмотренная на рис. 3.3 МIMO система аналогична системе связи с фидерами. Традиционная (SISO – Single Input Suingle Output) система связи с одним пространственным каналом - это аналог проводной системы с одним фидером. Это сравнение MIMO- и SISO-систем иллюстрирует рис. 3.4.

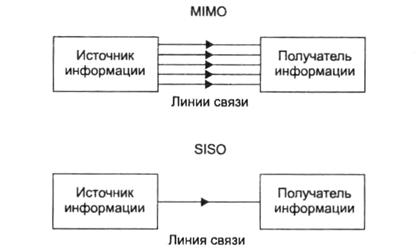
Рис. 3.4. Многопроводная и однопроводная линии связи – аналоги MIMO- и SISCO-систем связи

Можно также дать иное пояснение принципу работы MIMO - системы на рис. 3.3, которое в большей степени опирается на физику и в меньшей – на математику. Приемную антенную систему на рис. 3.3 вместе с пространственным декодером можно рассматривагь как антенную решетку с многолучевой диаграммой направленности. Причем каждый из лучей формируется так, чтобы он был направлен только на одну приемную антенну, на все остальные антенны должны быть направлены нули сформированного луча. На рис. 3.5 схематично показана двухлучевая диаграмма направленности с темным и светлым лучами.

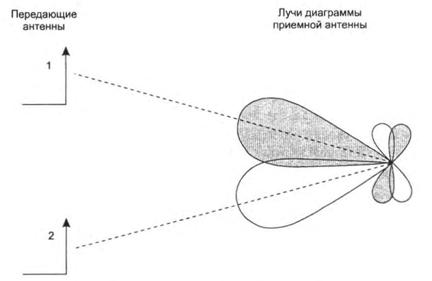
Рис. 3.5. Физическая иллюстрация разделения пространственно разнесенных источников

Темный луч обеспечивает прием сигнала от первой передающей антенны и не принимает сигналы второй антенны. Светлый луч, наоборот, принимает сигналы только от второй передающей антенны. В этой трактовке пространственное разделение источников объяснятся сложным характером диаграммы направленности антенной системы приемника. Конечно, следует учитывать, что в формировании диаграммы участвуют не только приемных антенн, но и многолучевая среда распространения волн. Приемник должен следить за изменением среды и постоянно менять положение лучей в пространстве.

Возможность одновременной передачи информации по нескольким пространственным каналам объясняет высокую спектральную эффективность многоантенных систем и пристальное внимание к ним со стороны разработчиков высокоскоростных систем радиосвязи.

3.2.2. Пропускная способность MIMO – систем

В этом разделе приведены известные из литературы формулы для расчета пропускной способности и спектральной эффективности MIMO – систем. Результаты расчетов и моделирования для различных MIMO – архитектур сравниваются между собой.

Вначале приведем формулу Шеннона для расчета удельной пропускной способности SISO - системы с одним пространственным каналом

(3.8)

В формуле (3.8) С - удельная пропускная способность, измеряемая в бит/с·Гц. Это максимальное количество бит, которые можно передать за одну секунду со сколь угодно малой вероятностью ошибки в полосе частот 1 Гц. Через SNR (Single to Noise Ratio) обозначено отношение мощности сигнала на входе приемника к мощности шума.

Для удельной пропускной способности MIMO - системы с передающими и приемными антеннами справедлива следующая формула [17]:

(3.9)

Входящие в формулу (3.9) величины - это собственные значения матрицы , т. е. величины, которые удовлетворяют уравнению

(3.10)

В (3.10) U - это собственный вектор матрицы . Через обозначена эрмитово сопряженная матрица, т. е. комплексно сопряженная и транспонированная. Известно, что все собственные значения матрицы неотрицательны.

Сравнение формул (3.9) и (3.8) подтверждает физические пояснения разд. 3.2.1. Действительно, MIMO - система эквивалентна - канальной системе связи. Ее пропускная способность определяется суммой слагаемых. Отношение мощности сигнала к мощности шума в канале с номером зависит от доли мощности, направляемой в этот канал при передаче (от ) и от значения . Из (3.9) виден физический смысл . Величина равна коэффициенту передачи по мощности соответствующего пространственного канала.

При равномерном распределении мощности между всеми пространственными каналами формула (3.9) принимает вид:

(3.11)

Вместо формулы (3.11) можно пользоваться эквивалентной ей формулой:

(3.11а)

В (3.11 а) I — единичная матрица и через det обозначен определитель записанной в скобках матрицы. Последняя формула позволяет вычислять удельную пропускную способность без вычисления собственных значений.

Для получения численных значений удельных пропускных способностей различных MIMO - систем выполнялось моделирование. При моделировании все фединги матрицы канала Н полагались независимыми гауссовыми случайными комплексными величинами с нулевыми средними значениями. Дисперсия их полагалась равной 1 (дисперсии мнимой и действительной частей по 1/2). То есть при моделировании генерировались случайных чисел, затем по формуле (3.11) или (3.11а) вычислялось значение C. Эта процедура многократно повторялась для различных случайных матриц Н и вычислялось среднее значение удельной пропускной способности, которое наносилось на график зависимости С(SNR).

Некоторые результаты моделирования приведены на рис. 3.6—3.9.

На рис. 3.6 приведены графики зависимости пропускной способности от SNR для MIMO - систем с двумя передающими () и с различным числом приемных антенн (). Для сравнения на графике приведена кривая для SISO системы (). Сравнение приведенных кривых показывает, что переход от SISO системы к MIMO дает значительное увеличение скорости передачи информации и это увеличение тем больше, чем больше число приемных антенн.

Выигрыш, получаемый при увеличении числа приемных антенн, можно характеризовать величиной уменьшения SNR в децибелах, при котором получается прежняя пропускная способность. Результат графического сравнения систем 2x2, 2x4 и 2x8 показан на рис. 3.7. Из рисунка видно, что три приведенные кривые приближенно совмещаются при смешении второй влево на -4,5 дБ и при смещении третьей на -8,5 дБ. То есть в MIMO - системе с двумя передающими антеннами переход от двух приемных антенн к четырем дает выигрыш примерно 4,5 дБ, а переход к восьми приемным антеннам примерно 8,5 дБ.

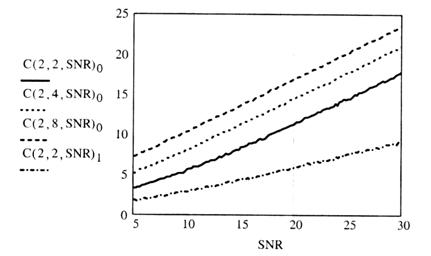
Рис. 3.6. Зависимость пропускной способности MIMO-систем от SNR

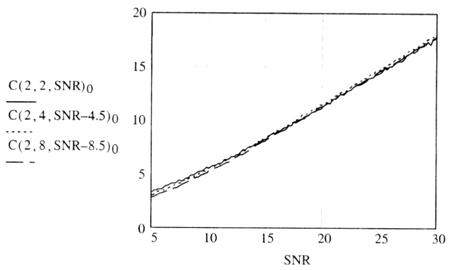
Рис. 3.7. Сравнение пропускной способности MIMO-систем при различном числе приемных антенн

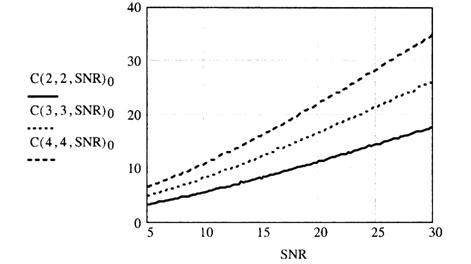
Рис. 3.8. Зависимость пропускной способности MIMO-систем от SNR при равном числе передающих и приемных антенн

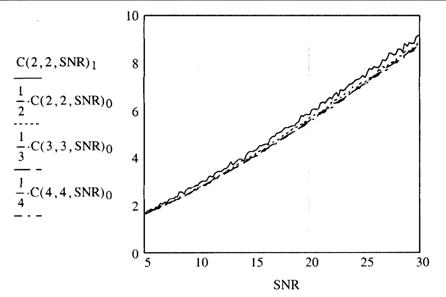
Рис. 3.9. Сравнение пропускной способности MIMO-систем при различном числе антенн

На рис. 3.8 рассмотрены MIMO - системы, когда число приемных антенн равно числу передающих (). Приведенные графики показывают, что пропускная способность растет с ростом числа антенн. Можно заметить, что пропускная способность MIMO - системы приближенно в раз больше пропускной способности 1x1 SISO - системы (по крайней мере, для больших SNR). Графическое подтверждение этого факта приведено на рис. 3.9. На этом рисунке приведены те же самые кривые, что и на рис. 3.8, но в отличие от них они поделены на число антенн . Также приведен график для 1x1 системы. Близость всех четырех кривых на рис. 3.9 подтверждает - кратное увеличение пропускной способности.

Численные результаты рис. 3.9 обосновывают справедливость аналогий на рис. 3.4, MIMO - система связи аналогична многопроводной линии связи, а SISO - однопроводной.

3.2.3. Алгоритм BLAST - пространственного декодирования

В этом разделе описан разработанный лабораторией Bell - Labs для многоантенной техники алгоритм BLAST (Bell Laborotories Layered Space-Time). Алгоритм имеет следующие модификации: D - BLAST и V - BLAST. Алгоритм D - BLAST позволяет, в принципе, получать более высокие скорости передачи информации, но более сложен в реализации. Так как потери в скорости при переходе от D - BLAST к более простому алгоритму V - BLAST невелики, то второму алгоритму отдается предпочтение. Изложение и обоснование алгоритма можно найти в работах [4, 21, 6, 5]. Краткое изложение алгоритма, которого мы будем придерживаться, можно найти в [2].

До изложения алгоритма поясним некоторые предположения и обозначения. Полагаем, что вектор принятых сигналов на выходе приемника связан с вектором излучаемых символов равенством:

(3.12)

Здесь I - дискретное время; - вектор размерности ; - вектор размерности ; - -мерный вектор шума; Н — матрица канала размерности .

В дальнейшем считается, что элементы матрицы канала не зависят от частоты, канал имеет плоскую частотную характеристику. Для всей используемой в WiMAX-системах полосы это предположение несправедливо. Однако при использовании OFDM это предположение справедливо для окрестности каждой поднесущей частоты. Полагается, что соотношение (3.12) и последующие формулы, используются на каждой поднесущей частоте и для каждой из них измерена и известна матрица Н.

Вектор в (3.12) - это независимых компонентов шума, то есть, соответствующая ему ковариационная матрица имеет вид:

Здесь - это дисперсия шума. Полагаем, что передача информации идет независимыми потоками, общая мощность между которыми распределена равномерно. Поскольку информационные потоки, которые также случайны, являются не связанными между собой, то ковариационная матрица вектора и имеет вид:

где - это средняя мощность сигнала, излучаемого одной антенной. Она связана с общей мощностью равенством:

Заметим, что SNR в формулах этой главы — это отношение средней мощности дисперсии шума:

Введем вектор ошибки , определяемый разностью между переданным вектором данных и его оценкой:

Задача минимизации среднего квадрата ошибки приводит к следующему решению. Для получения оптимальной оценки выходной вектор следует пропустить через фильтр (MMSE - фильтр), определяемый матрицей G:

(3.13)

Здесь - действительный параметр регуляризации, равный:

(3.14)

Вместо выражения (2.13) можно пользоваться иным, более компактным выражением:

(3.15)

Выражение (3.15), называемое псевдоинверсией, отличается от (3.13) отсутствием регуляризирующей диагональной матрицы . Отсутствие регуляризации приводит к увеличению шумов, особенно если матрица является плохо обусловленной. Поэтому использование (3.13) с ненулевым значением а предпочтительнее, чем (3.15), даже если дисперсия шума точно неизвестна.

В V – BLAST - алгоритме детектирование переданных символов (оценка вектора ) выполняется за итераций. Порядок, в котором извлекаются символы (компоненты вектора ), существенно влияет на характеристики системы.

На каждой итерации выполняются три шага.

Шаг 1. Подсчет оценки вектора с использованием MMSE-фильтра (3.13) или псевдоинверсии (3.15)

(3.16)

Шаг 2. Оценка того символа вектора , для которого значение SNR является наибольшим. Номер этого элемента определяется номером наименьшего диагонального элемента матрицы Q (3.13) при использовании MMSE - фильтра или номером столбца с наименьшей нормой при псевдоинверсии (3.15). Обозначим этот номер и найдем оценку символа :

(3.17)

В (3.17) через обозначена операция выбора сигнала, который наиболее близок к , в используемой сигнально-кодовой конструкции

Шаг 3. Модификация вектора и матрицы канала Н. Из вектора удаляется результат воздействия символа :

Здесь через обозначен столбец с номером матрицы Н. Матрица канала Н модифицируется удалением из нее столбца с номером .

Шаги 1—3 повторяются раз и вычисляются компоненты Более кратко и строго алгоритм V - BLAST приведен далее.

Инициализация:

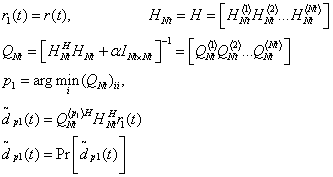
Рекурсия:

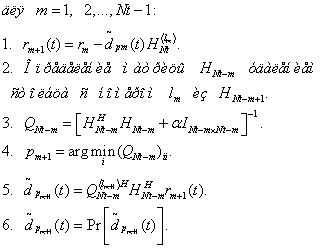
Результат вычислений:

Оценки излучённых сигналов:

В литературе [4] приводятся не только результаты теоретических расчетов и моделирования, но результаты экспериментов, подтверждающие работоспособность алгоритма V - BLAST и высокую спектральную эффективность MIMO - техники.

3.2.4. Неадаптивная многоантенная техника с числом передающих антенн большим, чем число приемных (MIMO + STBC)

Приведенный в предыдущем разделе алгоритм BLAST применим в том случае, если число передающих антенн не превышает число приемных. Только в

• система из разд. 3.2.4, сочетающая МГМО- и STBC-техники;
• идеальная адаптивная система с точным знанием канала в передатчике.

Как видно из рис. 3.16, адаптивный выбор наилучшей пары из четырех передающих антенн дает несколько лучшие характеристики, чем сочетание MIMO и STBC. Подчеркнем, что это улучшение достигается за счет введения обратной связи от приемника к передатчику. Количественные значения результатов сравнения удобно наблюдать на рис. 3.17. Из него видно, что система 4x2 с выбором проигрывает идеальной адаптивной 2 дБ, a MIMO+STBC проигрывает ей около 3 дБ.

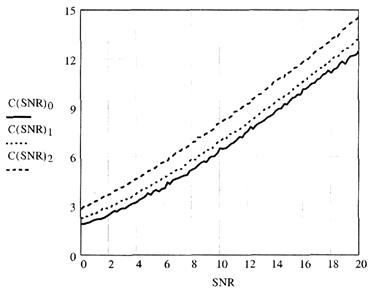
Рис 3.16. Зависимость пропускной способности от SNR для 4x2 MIMO-систем

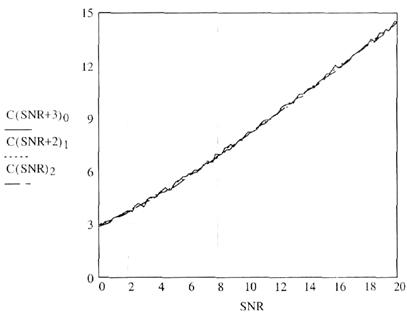
Рис. 3.17. Сравнение пропускной способности 4x2 MIMO-систем при различных способах передачи.

3.2.5. Адаптивная модуляция и адаптивное кодирование в многоантенных системах

Из предыдущих разделов главы видно, что в многоантенных системах среди пространственных каналов могут быть сильные и слабые подканалы, точнее, подканалы с высоким и низким SNR. Передатчик, не знающий свойств подканалов, передает информацию по ним с одинаковой скоростью. Это приводит к высокой вероятности ошибок в каналах с малым SNR. За счет этого общая вероятность ошибок увеличивается и характеристики системы ухудшаются. Для WiMAX-систем, использующих OFDM, эта проблема особенно важна, так как при большом количестве пространственно-частотных каналов вероятность появления слабых каналов особенно велика.

Простой и достаточно эффективный путь уменьшения влияния слабых каналов на характеристики системы — это перемежение. Перемежение — это тот же способ, который используется для уменьшения влияния временных замираний в канале. При перемежении передаваемые символы в передатчике переставляются, сдвигаются на различные временные интервалы, длительность которых превышает продолжительность замираний. В приемнике, где закон перемежения известен, исходный порядок передачи символов восстанавливается. При восстановлении сгруппированные из-за замираний ошибки становятся одиночными и устраняются при декодировании. Аналогичным образом перемежение используется в WiMAX-системах и уменьшает влияние слабых пространственно-частотных каналов на рост вероятности ошибок, Причем сообщается [13], что сочетание пространственного и частотного перемежения более эффективно, чем раздельное перемежение по частотным и пространственным каналам.

Метод перемежения выравнивает слабые и сильные каналы и делает возможной передачу информации в параллельных каналах при существенно различных SNR. Однако он не является оптимальным. Лучшие характеристики можно получить, если более интенсивно использовать канал с высоким SNR, менее интенсивно с меньшим SNR и совсем не использовать канал с малым SNR. Результаты моделирования, иллюстрирующие, что отказ от использования слабого канала может улучшить характеристики, представлен на рис. 3.18. На этом рисунке изображены зависимости удельной пропускной способности от SNR для системы 3x3. Одна кривая построена при условии, что используются все три пространственных канала и мощность передатчика делится поровну между тремя каналами. Вторая кривая построена при условии, что самый слабый канал не используется и мощность делится между двумя наиболее сильными каналами.

Как видно из графиков на рис. 3.18, при SNR < 12 дБ использование двух пространственных каналов более выгодно, чем трех. Лишь при SNR > 12 дБ появляется выигрыш от использования третьего наиболее слабого пространственного канала.

Строгое решение задачи об оптимальном распределении мощности в параллельных каналах для достижения максимальной пропускной способности изложено в работе К. Шеннона [16, 29]. Приведенный им алгоритм называется "водоналивным" алгоритмом и имеет наглядную физическую интерпретацию. Для нахождения оптимального распределения мощности по параллельным каналам следует построить график зависимости от номера i канала отношения σ_i²/λ_i. Здесь σ_i² — дисперсия шума в i-ом канале; λ_i — коэффициент передачи по мощности канала с номером i. График этой функции изображен на рис. 3.19 и трактуется в "водоналивном" алгоритме как дно бассейна.

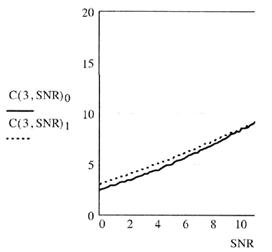
Рис. 3.18. Зависимость от SNR пропускной способности 3x3 MIMO-системы с тремя и двумя пространственными каналами

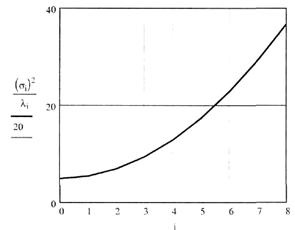
Рис. 3.19. Иллюстрация к "водоналивному" алгоритму оптимального распределения мощности в пространственных каналах.

Этот бассейн следует заполнить водой. Причем чем больше общая мощность, тем больше воды должно быть налито в бассейн. Расстояние от верхнего уровня до дна бассейна ("глубина") соответствует оптимальному значению мощности. Каналу с наибольшим SNR соответствует наибольшая "глубина", и в него должна направляться наибольшая мощность. В каналы с меньшим SNR будет направляться меньшая мощность. И если SNR канала настолько мало, что для него отношение σ_i²/λ_i окажется выше "уровня воды", то этот канал не следует использовать для передачи информации.

На практике для приближения к предельно возможной скорости передачи информации используют различные способы модуляции и кодирования в различных пространственно-частотных каналах. Такой способ передачи информации называется адаптивной модуляцией и адаптивным кодированием. Алгоритмы расчета адаптивной загрузки пространственно-частотных каналов описаны в [19]. Там приведены аналитические выражения и результаты моделирования для адаптивной системы, использующей 64-QAM. 16-QAM, QPSK в зависимости от состояния канала. Адаптивная система сравнивается с неадаптивной, использующей только QPSK. Для системы 4x4 при вероятности битовой ошибки 10^-3 экономия мощности за счет адаптации составляет 9 дБ. То есть знание состояния канала в передатчике и использование адаптивной модуляции и адаптивного кодирования позволяют в ряде случаев существенно улучшить характеристики системы связи.

Отметим еще одну важную для многоантенных систем связи задачу, при решении которой принципиально необходимо знание канала в передатчике. Это задача передачи информации различным пространственно разнесенным пользователям. Причем от многоантенной базовой станции информация может передаваться всем пользователям одновременно в одной и той же полосе частот без кодового разделения. Для разделения используется только пространственное разнесение приемников. Такие системы называют обычно системами множественного доступа с пространственным разделением (SDMA — Space-Diversity Multiple Access). SDMA-систему можно представить, как MIMO-систему, в которой на входе, на базовой станции есть много антенн, расположенных близко друг другу, а на выходе — множество антенн пользователей, которые расположены далеко друг от друга. Поэтому в SDMA-системах, в отличие от MIMO-техники, не может использоваться совместная обработка принимаемых сигналов. Здесь вся обработка должна быть сосредоточена на базовой станции. Излучаемые передающими антеннами сигналы должны быть сформированы так, чтобы информация, предназначенная для первого пользователя, попадала только первому пользователю и не попадала к остальным. Физически это означает, что в передатчике следует сформировать многолучевую диаграмму направленности. Причем нули диаграммы направленности луча должны быть направлены на всех пользователей, кроме одного: того, для которого этот луч передает информацию. Математически, если число пользователей и число передающих антенн одинаково, то предназначенные пользователю сигналы (вектор s) можно преобразовать в совокупность излучаемых сигналов (вектор и) таким образом:

u = H^-1s.

Здесь Н — матрица коэффициентов передачи канала. Тогда после прохождения через канал принятые сигналы (вектор г) совпадут с предназначенными пользователям сигналами s, если не учитывать шум:

r = Hu = s.

Если число пользователей меньше, чем число антенн на базовой станции, то излучаемые сигналы могут определяться через обобщенную обратную матрицу:

u = Н^Н(НН^Н)^-1s.

Несложно видеть, что если пренебречь влиянием шума, то и в этом случае равенство (3.28) остается справедливым.

Предварительное преобразование сигналов в передатчике называют предварительным кодированием (precoder). Ряд алгоритмов предварительного кодирования приведен в [19]. Для применения предварительного кодирования необходимо знание матрицы канала в передатчике. Только при этом условии возможно построение многоантенных SDMA-систем связи с высокой спектральной эффективностью.