8.1.1. Резонансные свойства П-образного контура

8.1.2. Методика расчета контура

8.1.3. Описание программ расчета П-образного контура при параллельном резонансе

8.1.4. Описание алгоритма программы расчета П-образного контура на ЭВМ

8.1.5. Настройка колебательной системы

Назначением выходных колебательных систем (ВКС) передатчиков являются:

• настройка в резонанс на рабочую частоту;
• согласование генератора с нагрузкой, которое заключается в том, что при любом сопротивлении нагрузки колебательной системы ее входное сопротивление должно быть равно требуемому значению эквивалентного сопротивления R_Э генераторной лампы;
• обеспечение требуемого коэффициента фильтрации высших гармоник.

С наибольшими трудностями сопряжено проектирование ВКС коротковолновых (КВ) передатчиков, поскольку эти передатчики работают в диапазоне частот более трех октав (3÷30МГц) при КБВ в антенном фидере К<1, поэтому входное сопротивление их нагрузки – антенного фидера - =r_ф ± jx_ф изменяется в весьма широких пределах. Как было показано в первой главе (п.1.14), область значений, которые могут принимать составляющие входного сопротивления фидера с волновым сопротивлением W и КБВ рабочей частоте К, определяется формулами:

r_ф= ,

± jW·(1- · , (8.1)

где –1 ≤ y ≤ +1.

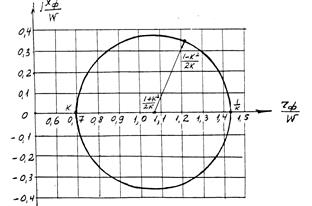
Рис.8.1.

Графически это представлено рис.8.1, где в качестве примера принят КБВ К=0,7 [1].

В зависимости от мощности передатчика используются одноконтурные и многоконтурные ВКС. В качестве одноконтурных ВКС в передатчиках мощностью до 15-20кВт используются П-образные контура, обеспечивающие хорошую фильтраию высших гармоник. В передатчиках мощностью до 500кВт используются двухконтурные ВКС с емкостной, либо с индуктивной связью - в зависимости от мощности передатчика. При построении оконечного каскада (ОК) передатчика по двухтактной схеме выходной контур двухконтурной ВКС всегда П-образный. При однотактном построении ОК оба контура ВКС могут быть П-образными. Для снижении уровня высших гармоник на входе ОК в качестве нагрузки предоконечного каскада (ПОК) часто используется также П-образный контур.

Точный расчет ВКС сопряжен с громоздкими вычислениями, поэтому он производится на ЭВМ. Ниже будут рассмотрены особенности настройки и расчета одноконтурных и двухконтурных ВКС, в состав которых входит П-образный контур, и описаны программы их расчета на ЭВМ.

Перечень программ расчета узкополосных колебательных систем,

Р0АМ - Расчет П-образного контура (П-контура) предоконечного каскада

(ПОК) при амплитудной модуляции (АМ).

Р0SB- Расчет П-образного контура (П-контура) предоконечного каскада (ПОК)

при однополосной модуляции (ОМ), колебания класса Н3Е

РСАM - расчет выходного П-контура, АМ.

РСАMF - расчет выходного П-контура c расчетом фильтрации высших гармоник

при АМ.

РCSB - расчет выходного П-контура, OM, H3E.

РLC1AM - расчет выходного П-контура и элемента связи двухконтурной выходной колебательной системы с емкостной или индуктивной связью (т.е. либо конденсатором связи С_св, либо с катушкой связи L_св, включенными между анодным и П-образным контурами) в однотактной схеме, АМ.

РLC2AМ - то же для двухтактной схемы.

PLC1SB - то же для однотактной схемы при ОМ, Н3Е.

PLC2SB - то же для двухтактной схемы при ОМ, Н3Е.

РL1AM- те же программы с расчетом фильтрации второй гармоники рабочей

частоты при индуктивной связи между контурами в однотактной схеме, АМ.

PL2AM - то же для двухтактной схемы при АМ.

PL1SB - то же для однотактной схемы при ОМ, Н3Е.

PL2SB - то же для двухтактной схемы при ОМ, Н3

PLК1 - те же программы, но при настройке однотактной колебательной системы при максимальном значении КБВ в соединительном фидере без расчета фильтрации высших гармоник.

PLК1AMF - этa же программa, дополненная расчетом фильтрации второй

гармоники колебательной системой с индуктивной связью между контурами в однотактной схеме генератора с амплитудной модуляцией.

PLК2AMF- этa же программа с расчетом фильтрации второй гармоники колебательной системой с индуктивной связью между контурами в двухтактной схеме генератора.

В качестве примера перечисленные выше программы (на языке БЕЙСИК), а также идентификации использованных в них символов, приведены в Приложении 6.

8.1.1. Резонансные свойства П-образного контура

П-образные контура широко используются в выходных цепях современных КВ передатчиков отечественных и зарубежных фирм для улучшения фильтрации высших гармоник. При их расчете следует иметь в виду, что в тех случаях, когда требуемое входное сопротивление настроенного контура меньше сопротивления его нагрузки, резонансные частоты нагруженного и ненагруженного П-контуров не совпадают.

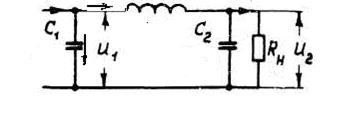
Рис.8.2

Резонансная частота нагруженного П-образного контура.

П-образный контур показан на рис.8.2. Его входное сопротивление определяется формулой:

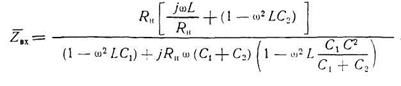(8.2)

(То, что здесь рассматривается случай активной нагрузки, т.е. Z_н=R_н, непринципиально, поскольку можно считать, что сопротивление Х_с2включает в себя реактивную составляющую сопротивления нагрузки; собственными потерями контура пренебрегаем, поскольку они всегда намного меньше вносимого сопротивления). Условием параллельного резонанса в контуре является равенство нулю реактивной составляющей входного сопротивления Z_вх, что приводит к биквадратному уравнению относительно резонансной частоты. В общем случае, когда нагрузкой контура является входное сопротивление антенного фидера Z_ф=r_ф ± jx_ф, решение этого уравнения можно представить в виде:

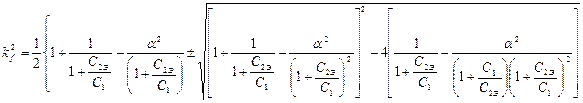
(8.3)

Здесь k_f= ω и ω₀ - частоты параллельного резонанса соответственно нагруженного и ненагруженного П-контура (R_н =∞):

, ,

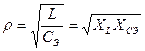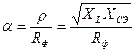, , R_Ф=r_Ф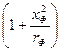 (8.4)

где Х_Ф – реактивная составляющая входной проводимости антенного фидера,

Х_СЭ - полное емкостное сопротивление контура, R_Ф - активная составляющая входной проводимости антенного фидера, r_Ф и х_Ф – активная и модуль реактивной составляющей его входного сопротивления, которые определяются формулами (8.1) и рис.8.1.Поскольку при α = 0 (R_н =∞) ω =ω₀ , то частота параллельного резонанса ненагруженного контура определяется формулой (8.3) со знаком « + » перед квадратным корнем. При частоте, которая определяется формулой (8.3) со знаком «−» перед квадратным корнем, в контуре имеет место частный резонанс (последовательный - в ветви L - C₂). Настройка П-контура на эту частоту является «ложной», хотя его сопротивление и в этом случае - чисто активное. При α = 0 (R_н = ∞), частота «ложной» наcтройки равна:

ω_л= (8.5)

На рис.8.3 изображены графики зависимости подкоренного выражения формулы (8.3), обозначенного, F(α), от параметра α при различных значениях отношения С₁/С₂. Из них видно, что при С₁/С₂>1 существует область значений α, при которых F(α) отрицательно, при этом П-образный контур становится апериодическим. Эта область тем шире, чем больше отличаются по величине емкости конденсаторов С₁ и С₂. При С₁=С₂. П-образный контур не становится апериодическим ни при каких значениях параметра α. Зависимость =f(α) при различных значениях С₁/С₂ также показана рис.8.3.

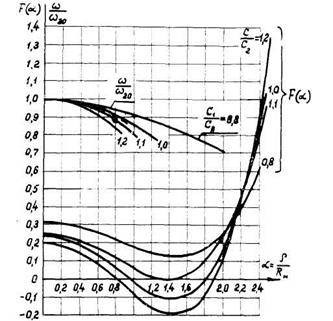
Рис.8.3

8.1.2. Методика расчета контура

Задачей расчета П-образного контура является обеспечение заданного коэффициента трансформации сопротивления нагрузки при таких значениях его реактивных элементов, при которых обеспечивается наибольший КПД и наилучшая фильтрация высших гармоник.

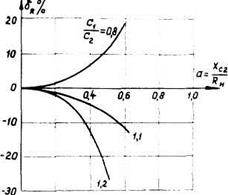
Рис.8.

Трансформация сопротивления

Входное сопротивление П-образного контура при резонансе на основании формул (8.1) и (8.4) определяется выражением:

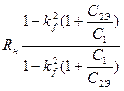= , (8.6)

откуда коэффициент трансформации сопротивления равен:

К_тр= = 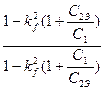(8.7)

При С₁=С₂ К_тр=1. Из выражения (8.7) следует, что при ω= ω₀

К_тр= =N² (8.8)

На рис.8.4 показаны графики относительной погрешности δ_R в определении коэффициента трансформации по формуле (8.8) в зависимости от параметра

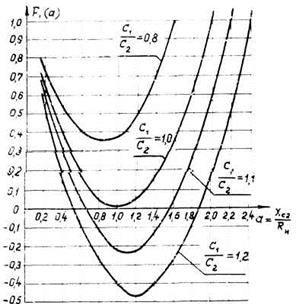
Рис.8.5

а= , характеризующего соотношение между реактивным сопротивлением выходной емкости С₂ П-контура на рабочей частоте и сопротивлением нагрузки R_н. Из рис.8.4 видно, что при малых значениях параметра а (а ≤0,4) погрешность не превышает 10-12%, что допустимо.

Расчет реактивного сопротивления катушки индуктивности

Реактивное сопротивление Х_L индуктивного элемента П-образного контура определяется в результате решения уравнения, полученного из условия равенства нулю реактивной составляющей входного сопротивления контура при резонансе (см.(8.2)). Реактивное сопротивление индуктивного элемента контура равно

X_L= 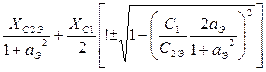(8.9)

Здесь:

а_Э= , (8.10)

где R_Ф=r_Ф 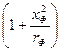- активная составляющая входной проводимости антенного фидера. Формула (8.9) со знаком «+» перед квадратным корнем определяет величину Х_L при параллельном резонансе, а та же формула со знаком «−» перед корнем определяет величину Х_L при «ложной настройке», когда входное сопротивление П-контура также активное, при С₁=С_2Э=С оно равно R_{вх.ложн.}= , а Х_Lллжн= . Из (8.9) видно, что при определенных значениях параметра а и отношения С₁/С₂ - обозначенное F₁(а) подкоренное выражение может оказаться отрицательным (рис.5). При F₁(а) < 0 П-контур становится апериодическим.

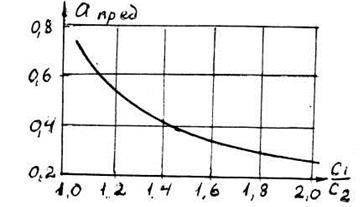
Рис.8.6

Приравняв нулю F₁(а) можно получить важную для практики зависимость предельных значений параметра аот отношения С₁/С₂: при а > а_пред П-контур становится апериодическим. Зависимость а_пред от С₁/С₂ приведена на рис.8.6

Добротность и КПД П-образного контура

КПД колебательного контураравен:

η = 1 − , (8.11)

где Q’ – добротность нагруженного, а Q₀ - добротность ненагруженного П-контура. По определению добротность есть отношение запаса реактивной мощности в контуре к мощности в нагрузке, поэтому добротность нагруженного П-контура равна:

Q’=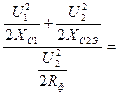

Принимая это во внимание и учитывая (8.7), получим:

Q’= 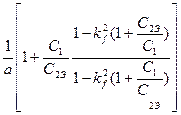(8.12)

В качестве примера на рис.8.7 приведены зависимости от параметра а= добротности Q’, КПД η и коэффициента фильтрации Ф_w симметричного П-образного контура, т.е. при С₁=С₂.

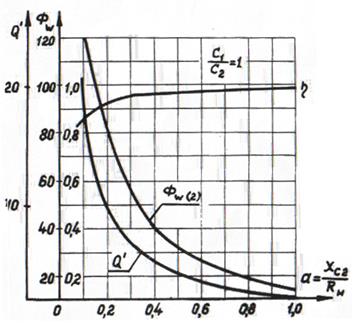
Рис.8.7

Расчет напряжений и токов в элементах П-образного контура при параллельном резонансе

Согласно рис.1 ток I_L через катушку индуктивности L равен:

= .

Напряжение U_L на катушке индуктивности равно:

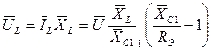, или .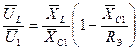

где φ₁ – угол между векторами и .

Так как мощности на входе и на выходе контура одинаковы, то:

, откуда 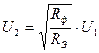(8.13)

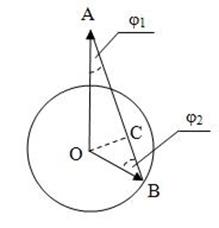
Рис.8.8

Величина U_L может быть найдена из векторной диаграммы рис.8.8 Ее построение начинают с вектора ОА=U₁, величина которого известна. Известен и угол φ₁между векторами и . Для нахождения величины из центра «О» строится окружность, радиус которой ОВ=U₂, величина которого известна. Из точки «O» опускается перпендикуляр ОС на отрезок АВ=U_L. Таким образом,

U_L=АС+ВС=U₁cosφ₁+ . (8.14)

Принимая во внимание, что , получим:

,

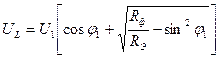или:

U_L=U₁cosφ₁+U₂ 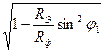= U₁cosφ₁+U₂ 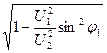, ( 8.14’)

где

. (8.15)

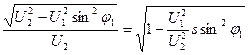Из векторной диаграммы следует, что cosφ₂ = , где ВС= , поэтому cosφ₂ = . Принимая во внимание ( 8.14’) напряжение U_L можно представить формулой:

U_L= U₁cosφ₁+U₂cosφ₂ , (8.16)

где

(8.17)

Амплитуда тока I_L через контурную катушку индуктивности равна:

(8.18)

8.1.3. Описание программ расчета П-образного контура при параллельном резонансе

Программы Р0 (Приложение 6.4).

Эти программы используются для расчета П-контуров, которые являются анодным контуром предоконечного, или другого резонансного промежуточного каскада высокочастотного тракта. В этом случае нагрузку контура можно считать активной, постоянной и равной входному сопротивлению последующего каскада: R_н = R_вх = U_gm/I_g1, где U_gm и I_g1 - соответственно, амплитуды напряжения возбуждения и первой гармоники сеточного тока последующего каскада. Согласование с нагрузкой производится емкостью С₁, а настройка в резонанс - изменением индуктивности L. Емкость С₂ выбирают так, чтобы ее реактивное сопротивление Х_с2 на всех частотах рабочего диапазона было постоянным (обычно X_c2 »(0,4-0,75)R_н). В программах рассчитываются параметры П-контура и максимальные значения напряжений и токов в его элементах.

1. Усиление мощности однотонового сигнала (УМ)

Напряжение на входной емкости П-контура равно:

U_c1= , (8.19)

где P - колебательная мощность, а R_э - эквивалентное сопротивление нагрузки лампы предыдущего каскада (P = P_g~- мощности возбуждения последующего каскада)

Напряжение на выходной емкости П-контура:

U_c2= , (8.20)

где R_н= R_вх - входному сопротивлению последующего каскада.

Напряжение на катушке индуктивности:

U_L= U_c1cosj₁ + U_c2cosj₂ , (8.21)

где

j₁ = arctg (X_c1/R_э),

j₂ = arctg (X_c2/R_н). (8.22)

Эффективные значения тока в элементах контура равны:

в конденсаторе С₁:

I_c1eff = 0,707× U_c1/X_c1 ,

в конденсаторе С₂:

I_c2eff = 0,707×U_c2/X_c2 ,

в катушке индуктивности L:

I_Leff = 0,707×U_L/X_L ,

2. Амплитудная модуляция.

При заданных значениях мощности возбуждения последующего каскада в максимальном режиме Р_g~max = Р_max напряжения на элементах контура в максимальном режиме определяются формулами (8.19) – (8.22) при Р=Р_max.

Эффективные значения тока в элементах контура во время модуляции определяются программой по формулам:

в конденсаторе С₁:

I_{c1efft max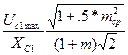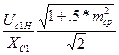} = = , (8.23)

в конденсаторе С₂:

I_{c2efft max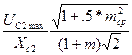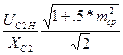} = = , (8.24)

в катушке индуктивности L:

I_{Lefft max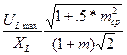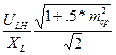} = = . (8.25)

Здесь m - глубина модуляции, m_ср- средняя глубина модуляции, U_c2max и U_Lmax -

напряжения на емкости С₂ и на катушке индуктивности в максимальном режиме. При m=1 и m_ср = 0,3 эффективные значения тока в элементах контура во время модуляции вычисляются в программе по формулам:

I_{efft max}=0,362×U_xmax /X , (8.26)

где U_xmax - напряжение в максимальном режиме на реактивном сопротивлении Х элемента контура. В результате расчета на ЭВМ определяется максимум I_efft.

Если задано напряжение в режиме несущей частоты U_н = , где Р_н - мощность в режиме несущей частоты, то

I_{efft max}= 0,725×U_н /X , (8.27)

3. Усиление однопололосного сигнала класса Н3Е

В однополосном режиме наибольшие потери на электродах лампы имеют место при сигнале класса Н3Е (см. [1], главу 5), поэтому расчет колебательной системы производится именно в этом режиме. Поскольку расчет усилителя мощности однополосного сигнала производится всегда в пиковом режиме, т.е. при однотоновом сигнале, то в результате этого расчета определяются максимальные значения напряжений на элементах контура. Тогда средние за период низкой частоты эффективные значения токов в элементах контура определяются следующим образом. Эффективное значение тока, среднее за период низкой частоты, равно:

I_efft = 0,707×I_effmax . (8.28)

Так как I_effmax = 0,707×I_max, где I_max - амплитуда тока в пиковом режиме, то

I_effmax = 0,5×I_max, и средние за период низкой частоты эффективные значения токов в элементах контура определяются формулами:

I_efft = 0,5×U_хmax/X. (8.29)

Здесь U_хmax - пиковые значения напряжений на элементах контура, конденсаторах или катушке индуктивности, а X - реактивное сопротивление этого элемента; из (29) пиковое значение напряжения на этом элементе контура равно:

U_хmax = 2×X×I_efft (8.30)

Программы РСАМ - РСSB

Эти программы предназначены для расчета П-контура, который является анодным контуром оконечного каскада, поэтому его нагрузка - входное сопротивление антенного фидера с заданными W и КБВ К₁. Во всех этих программах рассчитываются минимальные и максимальные значения реактивных сопротивлений элементов контура (в Омах), а также максимальные значения напряжений и токов в его элементах.

1. Амплитудная модуляция.

При заданной мощности в максимальном режиме Р=Р_~max напряжения на элементах контура в максимальном режиме определяются формулами (8.19) – (8.22), где

Р= Р_max, R_н = R_ф, а R_нmax = R_вхфmax - максимальное значение активной составляющей входной проводимости антенного фидера [1], которое равно:

R_вхфmax =W/K.

Эффективные значения тока в элементах контура во время модуляции определяются программой по формулам (8.23)

2. Усиление однополосного сигнала класса Н3Е.

Средние за период низкой частоты эффективные значения токов в элементах П-контура и пиковые значения напряжений на этих элементах рассчитывают по формулам (8.29) и (8.30).

8.1.4. Описание алгоритма программы расчета П-образного контура на ЭВМ

Алгоритм программы расчета П-образного контура, нагрузкой которого является входное сопротивление антенного фидера, приведен на рис.8.9. Использованная в качестве примера программа PCSB (на языке БЕЙСИК) и идентификация использованных в ней символов приведены в Приложении 6.1. Расчет производится для всех значений входного сопротивления антенного фидера c волновым сопротивлением фидера W и КБВ К₁. В блоке «1» (в программе – метки 2-9) задаются исходные данные. В блоках «2»–«13»в цикле по Y при Y0 ≤ Y ≤ Y1 c шагом ΔY (в программе – метки 10-35) производится расчет активной и реактивной составляющих входного сопротивления фидера, r_ф и ±jx_ф, которые определяются формулами (8.1), активной и реактивной составляющих его входной проводимости, R_ф и ±jX_ф, при этом во внутреннем цикле по J (блоки «4» – «11», в программе метки (14) - (33)) при J=1 и J=2, определяются требуемые значения коэффициента трансформации сопротивления К₀ при +jX_ф и –jX_ф (по формулам (8.4) – (8.7)), а также значения эквивалентного параметра а_Э (формула (8.10), в программе – метка 21) . Реактивные сопротивления входной емкости С₁ и индуктивности L П-контура (по формуле (8.9)), при которых коэффициент трансформации сопротивления К_тр=К₀, находят методом итераций в подпрограмме RAS1 (блок «8», в программе – метки 48-80). В блоке «10» (в программе метки 24-31) производится расчет напряжений и токов в П-контуре, а также его добротности. Далее в блоке «11» (в программе метки 32-39) определяются максимальные и минимальные значения реактивных сопротивлений Х_С1 и Х_L, а также максимальные напряжения и токи в элементах колебательного контура и его наибольшая добротность. В Приложении 6.1 в качестве примера приведена также программа PCAMF, в которой производится расчет коэффициента фильтрации Ф_w и экстремального значения мощности второй гармоники Р₂ на входе антенного фидера (блок 15), в программе - метки «47»-«60», где производится расчет параметров выходного П-контура при КБВ в фидере К₁=1 (см. п.8.4).

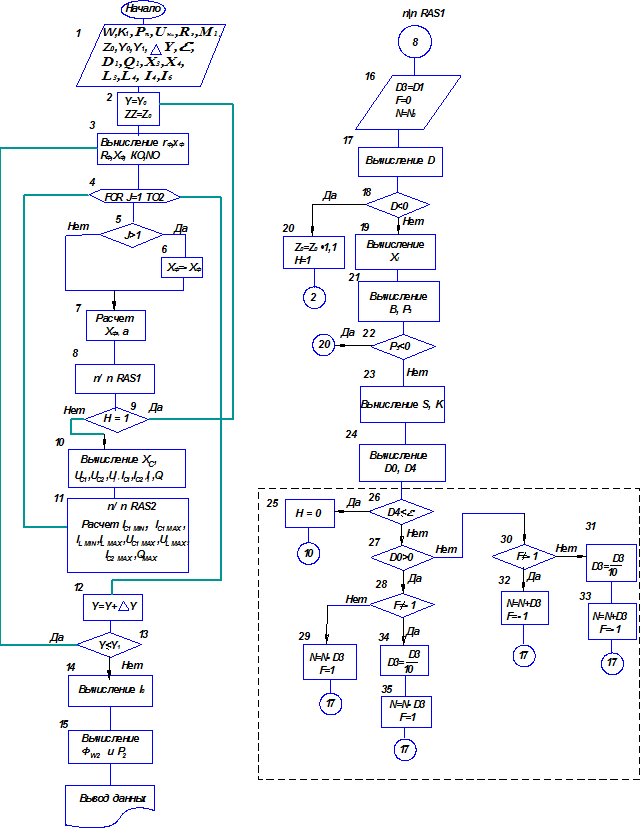
Рис.8.9

8.1.5. Настройка колебательной системы

Для лучшей фильтрации высших гармоник величина реактивного сопротивления Х_с2 выходной емкости С₂ П-контура на всех частотах рабочего диапазона должна быть постоянной, обычно выбирается Х_с2=(0,4÷0,75)W. В процессе согласования емкость С₂ не изменяется, поэтому согласование, т.е. обеспечение требуемого значения входного сопротивления контура R_вх=R_э, производится изменением его входной емкости C₁, после чего изменением индуктивности контура L восстанавливают настройку контура в резонанс.