13.1.2. Источники волновых сигналов
Кодирование источника связано с задачей создания эффективного описания исходной информации. Эффективное описание допускает снижение требований к памяти или полосе частот, связанных с хранением или передачей дискретных реализаций исходных данных. Для дискретных источников способность к созданию описаний данных со сниженной скоростью передачи зависит от информационного содержимого и статистической корреляции исходных символов. Для аналоговых источников способность к созданию описаний данных со сниженной скоростью передачи (согласно принятому критерию точности) зависит от распределения амплитуд и временной корреляции волнового сигнала источника. Целью кодирования источника является получение описания исходной информации с хорошей точностью при данной номинальной скорости передачи битов или допуск низкой скорости передачи битов, чтобы получить описание источника с заданной точностью. Чтобы понять, где эффективны методы и средства кодирования источника, важно иметь общие меры исходных параметров. По этой причине в данном разделе изучаются простые модели дискретных и аналоговых источников, а затем дается описание того, как кодирование источника может быть применено к этим моделям.
13.1.1. Дискретные источники
Дискретные источники генерируют (или выдают) последовательность символов Х(k), выбранную из исходного алфавита в дискретные промежутки времени kT, где k=1, 2, ... — счетные индексы. Если алфавит содержит конечное число символов, скажем N, говорят, что источник является конечным дискретным (finite discrete source). Примером такого источника является выход 12-битового цифро-аналогового преобразователя (один из 4096 дискретных уровней) или выход 10-битового аналого-цифрового преобразователя (один из 1024 двоичных 10-кортежей). Еще одним примером дискретного источника может послужить последовательность 8-битовых ASCII-символов, введенных с клавиатуры компьютера.
Конечный дискретный источник определяется последовательностью символов (иногда называемых алфавитом) и вероятностью, присвоенной этим символам (или буквам). Будем предполагать, что источник кратковременно стационарный, т.е. присвоенные вероятности являются фиксированными в течение периода наблюдения. Пример, в котором алфавит фиксирован, а присвоенные вероятности изменяются, — это последовательность символов, генерируемая клавиатурой, когда кто-то печатает английский текст, за которым следует печать испанского и наконец французского текстов.
Если известно, что вероятность каждого символа Xj есть Р(Хj), можно определить самоинформацию (self-information) I(Xj) для каждого символа алфавита.
(13.1)
Средней самоинформацией для символов алфавита, называемой также энтропией источника (source entropy), является следующее.
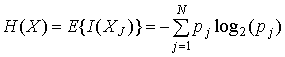(13.2)
где Е{Х} — математическое ожидание X. Энтропия источника определяется как среднее количество информации на выход источника. Энтропия источника — это средний объем неопределенности, которая может быть разрешена с использованием алфавита. Таким образом, это среднее количество информации, которое должно быть отправлено через канал связи для разрешения этой неопределенности. Можно показать, что это количество информации в битах на символ ограничено снизу нулем, если не существует неопределенности, и сверху log2(N), если неопределенность максимальна.
(13.3)
Пример 13.1. Энтропия двоичного источника
Рассмотрим двоичный источник, который генерирует независимые символы 0 и 1 с вероятностями р и (1 —р). Этот источник описан в разделе 7.4.2, а его функция энтропии представлена на рис. 7.5. Если р = 0,1 и (1 — р) = 0,9, энтропия источника равна следующему.
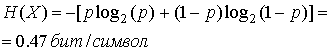(13.4)
Таким образом, этот источник может быть описан (при использовании соответствующего кодирования) с помощью менее половины бита на символ, а не одного бита на символ, как в текущей форме.
Отметим, что первая причина, по которой кодирование источника работает, — это то, что информационное содержание N-символьного алфавита, используемое в действительных системах связи, обычно меньше верхнего предела соотношения (13.3). Известно, что, как отмечено в примере 7.1, символы английского текста не являются равновероятными. Например, высокая вероятность конкретных букв в тексте используется как часть стратегии игры Хенгмана (Hangman). (В этой игре игрок должен угадывать буквы, но не их позиции в скрытом слове известной длины. За неверные предположения назначаются штрафы, а буквы всего слова должны быть определены до того, как произойдет шесть неверных предположений.)
Дискретный источник называется источником без памяти (memoryless), если символы, генерируемые источником, являются статистически независимыми. В частности, это означает, что их совместная вероятность двух символов является просто произведением вероятностей соответствующих символов.
(13.5)
Следствием статистической независимости есть то, что информация, требуемая для передачи последовательности М символов (называемой M-кортежем) данного алфавита, точно в М раз превышает среднюю информацию, необходимую для передачи отдельного символа. Это объясняется тем, что вероятность статистически независимого М-кортежа задается следующим образом.
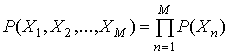(13.6)
Поэтому средняя на символ энтропия статистически независимого М-кортежа равна следующему.
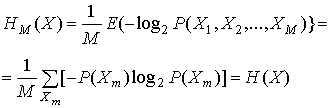(13.7)
Говорят, что дискретный источник имеет память, если элементы источника, образующие последовательность, не являются независимыми. Зависимость символов означает, что для последовательности M символов неопределенность относительно M-го символа уменьшается, если известны предыдущие (М-1) символов. Например, большая ли неопределенность существует для следующего символа последовательности CALIFORNI_? M-кортеж с зависимыми символами содержит меньше информации или разрешает меньше неопределенности, чем кортеж с независимыми символами. Энтропией источника с памятью является следующий предел.
(13-8)
Видим, что энтропия М-кортежа из источника с памятью всегда меньше, чем энтропия источника с тем же алфавитом и вероятностью символов, но без памяти.
(13.9)
Например, известно, что при данном символе (или букве) "q" в английском тексте следующим символом, вероятно, будет "u". Следовательно, в контексте системы связи, если сказать, что буква "u" следует за буквой "q", то это дает незначительную дополнительную информацию о значении слова, которое было передано. Можно привести и другой пример. Наиболее вероятным символом, следующим за буквами "th", может быть один из таких символов: а, е, i, о, u, r и пробел. Таким образом, дополнение следующим символом данного множества разрешает некоторую неопределенность, но не очень сильно. Формальная формулировка сказанного выше: средняя энтропия на символ М-кортежа из источника с памятью убывает при увеличении длины М. Следствие: более эффективным является групповое кодирование символов из источника с памятью, а не кодирование их по одному. При кодировании источника размер последовательности символов, рассматриваемой как группа, ограничивается сложностью кодера, ограничениями памяти и допустимой задержкой времени.
Чтобы помочь понять цели, преследуемые при кодировании источников с памятью, построим простые модели этих источников. Одна из таких моделей называется Марковским источником первого порядка (first-order Markov source) [1]. Эта модель устанавливает соответствие между множеством состояний (или символов в контексте теории информации) и условными вероятностями перехода к каждому последующему состоянию. В модели первого порядка переходные вероятности зависят только от настоящего состояния. Иными словами, P(Xi+1|Xi, Xi-1, ...) = P(Xi+1|Xi). Память модели не распространяется дальше настоящего состояния. В контексте двоичной последовательности это выражение описывает вероятность следующего бита при данном значении текущего бита.
Пример 13.2. Энтропия двоичного источника с памятью
Рассмотрим двоичный (т.е. двухсимвольный) Марковский источник второго порядка, описанный диаграммой состояний, изображенной на рис. 13.1. Источник определен вероятностями переходов состояний Р(0|1) и P(l|0), равными 0,45 и 0,05. Энтропия источника X — это взвешенная сумма условных энтропии, соответствующих вероятностям переходов модели.
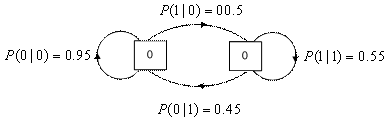
Рис. 13.1. Диаграмма переходов от состояния к состоянию для Марковской модели первого порядка
(13.10)
где
и
Априорная вероятность каждого состояния находится с помощью формулы полной вероятности.
Вычисляя априорные вероятности с использованием переходных вероятностей, получим следующее.
При вычислении энтропии источника с использованием равенства (13.10) получим следующее.
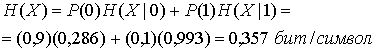
Сравнивая этот результат с результатом примера 13.1, видим, что источник с памятью имеет энтропию ниже, чем источник без памяти, даже несмотря на то что априорные вероятности символов те же.
Пример 13.3. Коды расширения
Алфавит двоичного Марковского источника (пример 13.2) состоит из 0 и 1, появляющихся с вероятностями 0,9 и 0,1, соответственно. Последовательные символы не являются независимыми, и для использования преимуществ этой зависимости можно определить новое множество кодовых символов — двоичные 2-кортежи (коды расширения).
Двоичные 2-кортежи Символ расширения Вероятность символа расширения
|
Двоичные 2-кортежи |
Символ расширения |
Вероятность символа расширения |
|
00 |
a |
Р(а) = Р(0|0)Р(0) = (0,95)(0,9) = 0,855 11 |
|
11 |
b |
Р(b) = Р(1| 1 )Р( 1) = (0,55)(0,1 ) = 0,055 |
|
01 |
c |
Р(с) = Р(0| 1 )Р( 1) = (0,45)(0,1 ) = 0,045 |
|
11 |
d |
Р(с) = Р(1| 0 )Р( 0) = (0,05)(0,9 ) = 0,045 |
Здесь крайняя правая цифра 2-кортежа является самой ранней. Энтропия для этого алфавита кодов расширения находится посредством обобщения равенства (13.10).
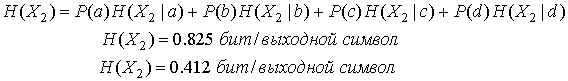
где Xk — расширение k-гo порядка источника X. Более длинный код расширения, использующий преимущества зависимости соседствующих символов, имеет следующий вид.
Двоичный 3-кортеж Символ расширения Вероятность символа расширения
|
Двоичные 2-кортежи |
Символ расширения |
Вероятность символа расширения |
|
000 |
a |
Р(а) = Р(0|00)P(00) = (0,95)(0,855) = 0,8123 |
|
100 |
b |
P(b) = P(1|00)P(00) = (0,05)(0,855) =0,0428 |
|
001 |
c |
P(с) = P(0|01)P(01) = (0,95)(0,045) = 0,0428 |
|
111 |
d |
P(d) = P(1|11)P(11) = (0,55)(0,055) =0,0303 |
|
110 |
e |
P(e) = P(1|10)P(10) = (0,55)(0,045) = 0,0248 |
|
011 |
f |
P(f) = P(0|11)P(1 1) = (0,45)(0,055) =0,0248 |
|
010 |
g |
P(g) = P(0|10)P(10) = (0,45)(0,045) = 0,0203 |
|
101 |
h |
P(h) = P(1|01)P(01) = (0,05)(0,045) = 0,0023 |
Используя снова обобщение уравнения (13.10), энтропию для этого кода расширения можно найти как
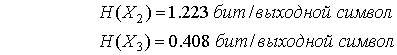
Отметим, что энтропия односимвольного, двухсимвольного и трехсимвольного описаний источника (0,470, 0,412 и 0,408 бит, соответственно) асимптотически убывает к энтропии источника, равной 0,357 бит/входной символ. Напомним, что энтропия источника — это нижний предел в битах на входной символ для этого алфавита (память бесконечна), и этот предел не может быть достигнут с помощью кодирования конечной длины.
13.1.2. Источники волновых сигналов
Источник волнового сигнала — это случайный процесс некоторой случайной переменной. Считается, что эта случайная переменная — время, так что рассматриваемый волновой сигнал — это изменяющийся во времени волновой сигнал. Важными примерами изменяющихся во времени волновых сигналов являются выходы датчиков, используемых для контроля процессов и описывающих такие физические величины, как температура, давление, скорость и сила ветра. Значительный интерес представляют такие примеры, как речь и музыка. Волновой сигнал может также быть функцией одной или более пространственных величин (т.е. расположение на плоскости с координатами х и у). Важными примерами пространственных волновых сигналов являются единичные зрительные образы, такие как фотография, или движущиеся зрительные образы, такие как последовательные кадры художественного фильма (24 кадра/с). Пространственные волновые сигналы часто преобразуются в изменяющиеся во времени волновые сигналы посредством сканирования. Например, это делается для систем факсимильной связи и передач в формате JPEG, а также для стандартных телевизионных передач.
13.1.2.1. Функции плотности амплитуд
Дискретные источники описываются путем перечисления их возможных элементов (называемых буквами алфавита) и с помощью их многомерных функций плотности вероятности (probability density function — pdf) всех порядков. По аналогии источники волновых сигналов подобным образом описываются в терминах их функций плотности вероятности, а также параметрами и функциями, определенными с помощью этих функций плотности вероятности. Многие волновые сигналы моделируются как случайные процессы с классическими функциями плотности вероятности и простыми корреляционными свойствами. В процессе моделирования различаются краткосрочные, или локальные (временные), характеристики и долгосрочные, или глобальные. Это деление необходимо, так как многие волновые сигналы являются нестационарными.
Функция плотности вероятности реального процесса может быть не известна разработчику системы. Конечно, в реальном времени для короткого предшествующего интервала можно быстро построить выборочные плотности и использовать их как разумные оценки в течение последующего интервала. Менее претенциозная задача — это создание краткосрочных средних параметров, связанных с волновыми сигналами. Эти параметры — выборочное среднее (или среднее по времени), выборочная дисперсия (или среднеквадратическое значение процесса с нулевым средним) и выборочные коэффициенты корреляции, построенные на предшествующем выборочном интервале. При анализе волновых сигналов входной волновой сигнал преобразуется в процесс с нулевым средним путем вычитания его среднего значения. Например, это происходит в устройствах сравнения сигналов, используемых в аналого-цифровых преобразователях, для которых вспомогательная схема измеряет внутренние смещения от уровня постоянного напряжения канала передачи данных и вычитает их в процессе, известном как автонуль (autozero). Далее оценка дисперсии часто используется для масштабирования входного волнового сигнала, чтобы сопоставить динамику размаха амплитуды последующего волнового сигнала, обусловленную схемой. Этот процесс, выполняемый при сборе данных, называется автоматической регулировкой усиления (automatic gain control — AGC, АРУ). Функцией этих операций, связанных с предварительным формированием сигналов, — вычитание среднего, контроль дисперсии или выравнивание усиления (показанных на рис. 13.2) — является нормирование функций плотности вероятности входного волнового сигнала. Это нормирование обеспечивает оптимальное использование ограниченного динамического диапазона последующих записывающих, передающих или обрабатывающих подсистем.
Многие источники волновых сигналов демонстрируют значительную корреляцию амплитуды на последовательных временных интервалах. Эта корреляция означает, что уровни сигнала на последовательных временных интервалах не являются независимыми. Если временные сигналы независимы на последовательных интервалах, автокорреляционная функция будет импульсной. Многие сигналы, представляющие инженерный интерес, имеют корреляционные функции конечной ширины. Эффективная ширина корреляционной функции (в секундах) называется временем корреляции процесса и подобна временной константе фильтра нижних частот. Этот временной интервал является показателем того, насколько большой сдвиг вдоль оси времени требуется для потери корреляции между данными. Если время корреляции большое, то это значит, что амплитуда волнового сигнала меняется медленно. Наоборот, если время корреляции мало, делаем вывод, что амплитуда волнового сигнала значительно меняется за очень малый промежуток времени.
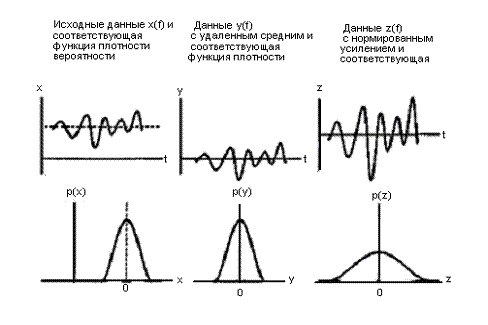
Рис. 13.2. Удаление среднего и нормирование дисперсии (регулировка усиления) для зависимых от данных систем предварительного формирования сигнала