Среди разновидностей систем управления важное место занимают системы логического управления (СЛУ). Характерным признаком этих систем является применение двоичных датчиков и исполнительных механизмов в виде источников входных и приемников выходных сигналов. При проектировании СЛУ широко используются микросхемы типа СИС и БИС, которые позволяют решать сложные функции и алгоритмы аппаратным (схемотехническим) путем. К числу таких микросхем относятся: арифметико-логические, расчетные и триггерные устройства, регистры, сумматоры, умножители, мультиплексоры, шифраторы, компараторы и др. Менее известны на практике проектирования мультиплексоры (MX), представляющие собой логическое устройство, которое содержит g- управляющих входов U₁, U₂,..., U_g; 2^g - информационных входов D0, D1, D2; стробирующий вход и выход. При подаче на управляющие входы комбинации двоичных сигналов и соответствующего сигнала на вход стробирования к выходу Y мультиплексора подключается тот информационный вход, порядковый номер которого отвечает весу двоичной комбинации управляющих сигналов. Построение логических схем на мультиплексорах проводится в виде структур, которые отличаются способами функционального распределения и разложения булевых функций (БФ). Наиболее часто на практике применяется разложение БФ по способу Шеннона:

,

где - остаточные функции разложения, которые получаются из функции путем подстановки констант 0 и 1 вместо сменных переменных множества . После проведения этой операции получим:

для имеем

для имеем

для _l имеем

Например, булева функция имеет вид

Для компактности записи заданной булевой функции используется десятичная форма записи с обозначением отдельных конъюнкций и представляет-ся в виде множества :

.

С учетом специфики работы мультиплексоров и конструктивных особенностей их реализации с числом управляющих входов g = 2,3,4 и информационных входов 2^g = 4,8,16 разложение заданной БФ можно осуществить по двум, трем или четырём переменным. Тогда при построении логической схемы на мультиплексорах переменные должны подключаться к управляющим входам, а остаточные функции (ОФ) разложения - к информационным входам соответ-ствующего MX. Если образованные в результате первого шага ОФ имеют нетривиальный вид, то процедура разложения каждой из них должна повторяться до момента тривиального вида, а именно:

0 (отсутствующая).

Остаточные функции разложения Q_t по последним двум , трем , четырем переменным с булевой функцией могут быть вычислены по формулам:

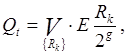
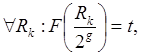
где t = 0,1,...,2 g-¹;

- целая часть от деления ;

- остаток от деления ;

- множество терминов БФ;

g - число переменных, на которые раскладывается БФ.

При построении логической схемы на MX, которые реализуют заданную БФ, возможны два случая:

a) n <= g;

б) n => g

В первом случае БФ реализуется схемой, состоящей из одного мультиплексора, в которой g переменных подключаются к управляющим входам MX, а на информационные входы подаются константы 0 или 1.

Во втором случае процесс построения логической схемы проводится по результатам разложения заданной БФ. Вследствие первого шага разложения исходной БФ по g переменным получаем совокупность ОФ, которая зависит только от n-g переменных. Следующие шаги разложения уменьшают каждый раз число переменных ОФ на g, вплоть до получения в процессе разложения ОФ тривиального вида. Таким образом, число шагов разложения БФ отвечает числу каскадов схемы на мультиплексорах с подключением на управляющие входы MX тех переменных, по которым осуществлялось разложение; на информационные входы MX последнего каскада подаются отдельные переменные или , а также сигналы логического 0 или логической 1, исходя из вида полученных ОФ:

Ǿ

Согласно приведенному выше алгоритму осуществим разложение заданной БФ по двум, трем и четырем переменным, сводя результаты расчетов в таблицы. Вариант разложения БФ по двум переменным приведен в табл. 4.1.

Таблица 4.1 – Результаты разложения БФ по двум переменным

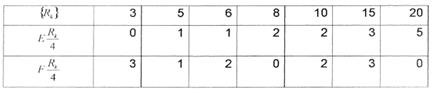
Таким образом, на первом шаге разложения БФ получаем следующие ОФ:

Разложение БФ продолжим, так как не все ОФ имеют тривиальный вид.

На втором шаге рассматривается каждая из полученных на первом шаге разложения остаточных функций Q_t (табл. 4.2).

Таблица 4.2 – Результаты разложения остаточных функций Q_t

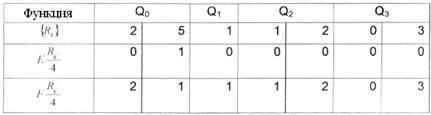
На втором шаге разложения БФ имеем следующую ОФ:

для Ǿ,

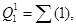
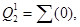
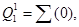
для Ǿ, Ǿ, Ǿ;

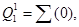
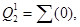
для Ǿ, Ǿ;

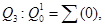
для Ǿ, Ǿ,

Так как ОФ, полученные на втором шаге разложения, являются тривиальными, проверим это практической реализацией построением двухкаскадной схемы на MX с g = 2. Схемная реализация БФ на MX типа К1533КП2 приведена на рис. 4.1. Вариант разложения БФ по трем переменным приведен в табл. 4.3.

Таблица 4.3 – Результаты разложения БФ по трем переменным

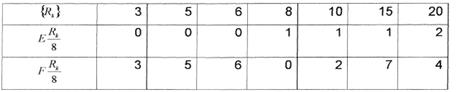
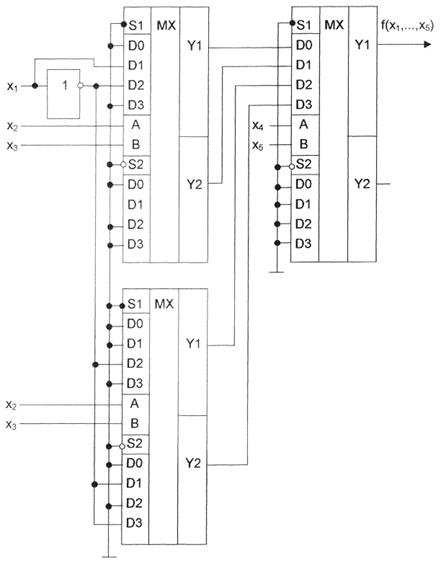
Рисунок 4.1. Реализация заданной БФ на мульти-плексорах типа К1533КП2

Таким образом, после первого разложения по трем переменным получены следующие ОФ:

Ǿ,

Поскольку одну часть ОФ получили тривиальной (Q₀ - Q₁, Q₅ - Q₇), a другую (Q₄) - нетривиальной, что свидетельствует о нецелесообразности дальнейшего разложения БФ и ее схемной реализации (для окончательной реализации БФ при таком подходе нужно иметь восемь мультиплексоров).

Вариант разложения БФ по четырем переменным приведен в табл. 4.4.

Таблица 4.4. Результаты разложения БФ по четырем переменным

Таким образом, после первого шага разложения БФ по четырем переменным получены следующие ОФ:

Q₀=Q₁=Q₂=Q₇=Q₉=Q₁₂=Q₁₃=Q₁₄=Ǿ, Q₃=Q₅=Q₆=Q₈=Q₁₀=Q₁₅= Ǿ,

Q₀=1.

Поскольку все ОФ тривиальные, разложение БФ заканчиваем и ее можно реализовать на одном MX при g=4. Схемная реализация заданной БФ на одном мультиплексоре типа К155КП1 приведена на рис. 4.2.

Для реализации на мультиплексорах лучше всего подходят БФ с числом переменных конъюнкций до 9.

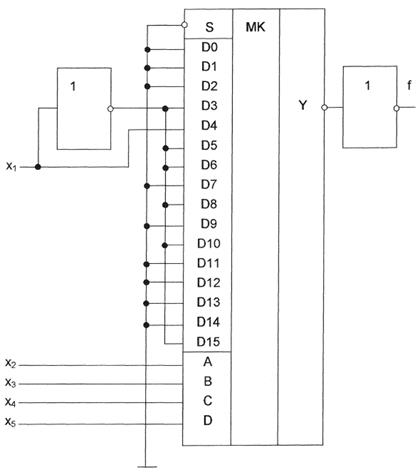
Рисунок 4.2. Реализация заданной БФ на мульти-плексоре типа К155КП1

Список литературы

1. Арсеньев Ю.Н., Журавлев В.М. Проектирование систем логического управления на микропроцессорных средствах. -М.: Высшая школа, 1991.

2. Закревский А.Д. Логический синтез каскадных схем. -М., 1981.

3. Юдицкий С.А., Тагаевская А.А., Ефремова Г.К. Проектирование дискретных систем автоматики. - М.: Высшая школа, 1980.