7.3.1. Декодирование по методу максимального правдоподобия

7.3.2. Модели каналов: мягкое или жесткое принятие решений

7.3.2.1. Двоичный симметричный канал

7.3.2.2. Гауссов канал

7.3.3. Алгоритм сверточного декодирования Витерби

7.3.4. Пример сверточного декодирования Витерби

7.3.5. Реализация декодера

7.3.5.1. Процедура сложения, сравнения и выбора

7.3.5.2. Вид процедуры сложения, сравнения и выбора на решетке

7.3.6. Память путей и синхронизация

7.3.1. Декодирование по методу максимального правдоподобия

Если все входные последовательности сообщений равновероятны, минимальная вероятность ошибки получается при использовании декодера, который сравнивает условные вероятности и выбирает максимальную. Условные вероятности также называют функциями правдоподобия, где Z — это принятая последовательность, а — одна из возможных переданных последовательностей. Декодер выбирает , если

по всем .

Принцип максимального правдоподобия, определяемый уравнением (7.1), является фундаментальным достижением теории принятия решений (см. приложение Б); это формализация способа принятия решений, основанного на "здравом смысле", когда имеются статистические данные о вероятностях. При рассмотрении двоичной демодуляции в главах 3 и 4, предполагалась передача только двух равновероятных сигналов и . Следовательно, принятие двоичного решения на основе принципа максимального правдоподобия, касающееся данного полученного сигнала, означает, что в качестве переданного сигнала выбирается , если

.

В противном случае считается, что передан был сигнал . Параметр z представляет собой величину , значение принятого сигнала до детектирования в конце каждого периода передачи символа t = Т. Однако при использовании принципа максимального правдоподобия в задаче сверточного декодирования, в сверточном коде обнаруживается наличие памяти (полученная последовательность является суперпозицией текущих и предыдущих двоичных разрядов). Таким образом, применение принципа максимального правдоподобия при декодировании бит данных, закодированных сверточным кодом, осуществляется в контексте выбора наиболее вероятной последовательности, как показано в уравнении (7.1). Обычно имеется множество возможных переданных последовательностей кодовых слов. Что касается двоичного кода, то последовательность из L ответвленных слов является членом набора из возможных последовательностей. Следовательно, в контексте максимального правдоподобия можно сказать, что в качестве переданной последовательности декодер выбирает , если вероятность больше вероятности всех остальных возможно переданных последовательностей. Такой оптимальный декодер, минимизирующий вероятность ошибки (когда все переданные последовательности равновероятны), известен как декодер, работающий по принципу максимального правдоподобия (maximum likelihood detector). Функция правдоподобия задается или вычисляется, исходя из спецификации канала.

Предположим, что мы имеем дело с аддитивным белым гауссовым шумом с нулевым средним в канале без памяти, т.е. шум влияет на каждый символ кода независимо от остальных символов. При степени кодирования сверточного кода, равной 1/n, правдоподобие можно выразить следующим образом.

(7.2)

Здесь — это -я ветвь полученной последовательности , — это ветвь отдельной последовательности кодовых слов — это й кодовый символ , а каждая ветвь состоит из n кодовых символов. Задача декодирования заключается в выборе пути сквозь решетку, показанную на рис. 7.7 (каждый возможный путь определяет последовательность кодовых слов), аким образом, чтобы произведение

(7.3)

Как правило, при вычислениях удобнее пользоваться логарифмом функции правдоподобия, поскольку это позволяет произведение заменить суммированием. Мы можем воспользоваться таким преобразованием, поскольку логарифм является монотонно возрастающей функцией и, следовательно, не внесет изменений в выбор окончательного кодового слова. Логарифмическую функцию правдоподобия можно определить следующим образом.

(7.4)

Теперь задача декодирования заключается в выборе пути вдоль дерева на рис. 7.6 или решетки на рис. 7.7 таким образом, чтобы было максимальным. При декодировании сверточных кодов можно использовать как древовидную, так и решетчатую структуру. При древовидном представлении кода игнорируется то, что пути снова объединяются. Для двоичного кода количество возможных последовательностей, состоящих из L ответвленных слов, равно . Поэтому декодирование полученных последовательностей, основанное на принципе максимального правдоподобия с использованием древовидной диаграммы, требует метода "грубой силы" или исчерпывающего сопоставления накопленных логарифмических метрик правдоподобия, описывающих все варианты возможных последовательностей кодовых слов. Поэтому рассматривать декодирование на основе принципа максимального правдоподобия с помощью древовидной структуры практически невозможно. В предыдущем разделе было показано, что при решетчатом представлении кода декодер можно построить так, чтобы можно было отказываться от путей, которые не могут быть кандидатами на роль максимально правдоподобной последовательности. Путь декодирования выбирается из некоего сокращенного набора выживших путей. Такой декодер тем не менее является оптимальным; в том смысле, что путь декодирования такой же, как и путь, полученный с помощью декодера критерия максимального правдоподобия, действующего "грубой силой", однако предварительный отказ от неудачных путей снижает сложность декодирования.

В качестве великолепного пособия для изучения структуры сверточных кодов, декодирования на основе критерия максимального правдоподобия и реализации кода можно порекомендовать работу [8]. Существует несколько алгоритмов, которые дают приблизительные решения задачи декодирования на основе критерия максимального правдоподобия, включая последовательный [9, 10] и пороговый [11]. Каждый из этих алгоритмов является подходящим для узкоспециальных задач; однако все они близки к оптимальному. Алгоритм декодирования Витерби, напротив, осуществляет декодирование на основе критерия максимального правдоподобия и, следовательно, является оптимальным. Это не означает, что алгоритм Витерби в любой реализации является наилучшим; при его использовании существуют жесткие условия, налагаемые на аппаратное обеспечение.

7.3.2. Модели каналов: мягкое или жесткое принятие решений

Перед тем как начать разговор об алгоритме, который задает схему принятия максимально правдоподобного решения, давайте сначала опишем канал. Последовательность кодовых слов , определяемую ответвленными словами, каждое из которых состоит из n кодовых символов, можно рассматривать как бесконечный поток, в отличие от блочного кода, где исходные данные и их кодовые слова делятся на блоки строго определенного размера. Последовательность кодовых слов, показанная на рис. 7.1, выдается сверточным кодером и подается на модулятор, где кодовые символы преобразуются в сигналы. Модуляция может быть узкополосной (например, модуляция импульсными сигналами) или полосовой (например, модуляция PSK или FSK). Вообще, за такт в сигнал преобразуется l символов, где l — целое, причем i = 1, 2,…, a . Если l = 1, модулятор преобразует каждый кодовый символ в двоичный сигнал. Предполагается, что канал, по которому передается сигнал, искажает сигнал гауссовым шумом. После того как искаженный сигнал принят, он сначала обрабатывается демодулятором, а затем подается на декодер.

Рассмотрим ситуацию, когда двоичный сигнал передается за отрезок времени (0, Т), причем двоичная единица представляется сигналом , а двоичный нуль — сигналом . Принятый сигнал имеет вид , где n(t) представляет собой вклад гауссового шума с нулевым средним. В главе 3 мы описывали обнаружение в два основных этапа. На первом этапе принятый сигнал переводится в число , где — это компонент сигнала z(T), a — компонент шума. Компонент шума п0 — это случайная переменная, значения которой имеют гауссово распределение с нулевым средним. Следовательно, также будет случайной гауссовой величиной со средним или , в зависимости от того, какая величина была отправлена — двоичная единица или двоичный нуль. На втором этапе процесса обнаружения принимается решение о том, какой сигнал был передан. Это решение принимается на основе сравнения z(T) с порогом. Условные вероятности , показанные на рис. 7.8, обозначены как правдоподобие и . Демодулятор, представленный на рис. 7.1, преобразует упорядоченный по времени набор случайных переменных в кодовую последовательность Z и подает ее на декодер. Выход демодулятора можно настроить по-разному. Можно реализовать его в виде жесткой схемы принятия решений относительно того, представляет ли z(T) единицу или нуль. В этом случае выход демодулятора квантуется на два уровня, нулевой и единичный, и соединяется с декодером (это абсолютно та же схема пороговых решений, о которой шла речь в главах 3 и 4). Поскольку декодер работает в режиме жесткой схемы принятия решений, принятых демодулятором, такое декодирование называется жестким.

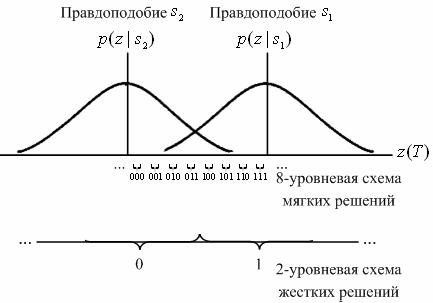
Рис. 7.8. Жесткая и мягкая схемы декодирования

Аналогично демодулятор можно настроить так, чтобы он подавал на декодер значение z(T), квантованное более чем на два уровня. Такая схема обеспечивает декодер большим количеством информации, чем жесткая схема решений. Если выход демодулятора имеет более двух уровней квантования, то декодирование называется мягким. На рис. 7.8 на оси абсцисс изображено восемь (3-битовых) уровней квантования. Если в демодуляторе реализована жесткая схема принятия двоичных решений, он отправляет на декодер только один двоичный символ. Если в демодуляторе реализована мягкая двоичная схема принятия решений, квантованная на восемь уровней, он отправляет на декодер 3-битовое слово, описывающее интервал, соответствующий . По сути, поступление такого 3-битового слова, вместо одного двоичного символа эквивалентно передаче декодеру меры достоверности вместе с решением относительно кодового символа. Согласно рис. 7.8, если с демодулятора поступила на декодер последовательность 111, это равносильно утверждению, что с очень высокой степенью достоверности кодовым символом была 1, в то время как переданная последовательность 100 равносильна утверждению, что с очень низкой степенью достоверности кодовым символом была 1. Совершенно ясно, что в конечном счете каждое решение, принятое декодером и касающееся сообщения, должно быть жестким; в противном случае на распечатках компьютера можно было бы увидеть нечто, подобное следующему: "думаю, это 1", "думаю, это 0" и т.д. То, что после демодулятора не принимается жесткое решение и на декодер поступает больше данных (мягкое принятие решений), можно понимать как промежуточный этап, необходимый для того, чтобы на декодер поступило больше информации, с помощью которой он затем сможет восстановить последовательность сообщения (с более высокой достоверностью передачи сообщения по сравнению с декодированием в рамках жесткой схемы принятия решений). Показанная на рис. 7.8, 8-уровневая метрика мягкой схемы принятия решений часто обозначается как -7, -5, -3, -1, 1, 3, 5, 7. Такие обозначения вводятся для простоты интерпретации мягкой схемы принятия решения. Знак метрики характеризует решение (например, выбирается , если величина положительна, и , если отрицательна), а величина метрики описывает степень достоверности этого решения. Преимуществом метрики, показанной на рис. 7.8, является только то, что в ней не используются отрицательные числа.

Для гауссова канала восьмиуровневое квантование, по сравнению с двухуровневым, приводит в результате к улучшению на 2 дБ требуемого отношения сигнал/шум. Это означает, что восьмиуровневое квантование с мягкой схемой принятия решений может дать ту же вероятность появления ошибочного бита, что и декодирование с жесткой схемой принятия решений, однако требует на 2 дБ меньшего значения при прочих равных характеристиках. Аналоговое квантование (или квантование с бесконечным числом уровней) дает в результате улучшение на 2,2 дБ, по сравнению с двухуровневым; следовательно, при восьмиуровневом квантовании, по сравнению с квантованием с бесконечным числом уровней, теряется приблизительно 0,2 дБ. По этой причине квантование более чем на восемь уровней может дать только небольшое улучшение производительности [12]. Какова цена, которую следует заплатить за такое улучшение параметров декодирования с мягкой схемой принятия решений? В случае декодирования с жесткой схемой принятия решений, для описания каждого кодового символа используется один бит, в то время как при восьмиуровневой мягкой схеме принятия решения для описания каждого символа применяется 3 бит; следовательно, в течение процесса декодирования нужно успеть обработать в три раза больше данных. Поэтому за мягкое декодирование приходится платить увеличением требуемых объемов памяти (и, возможно, возникнут проблемы со скоростью обработки).

В настоящее время существуют блочные и сверточные алгоритмы декодирования, функционирующие на основе жесткой или мягкой схемы принятия решений. Однако при блочном декодировании мягкая схема принятия решений, как правило, не используется, поскольку ее значительно сложнее реализовать, чем схему жесткого принятия решений. Чаще всего мягкая схема принятия решений применяется в алгоритме сверточного декодирования Витерби, поскольку при декодировании Витерби мягкое принятие решений лишь незначительно усложняет вычисления.

7.3.2.1. Двоичный симметричный канал

Двоичный симметричный канал (binary symmetric channel - BSC) — это дискретный канал без памяти (см. раздел 6.3.1), имеющий на входе и выходе двоичный алфавит и симметричные вероятности перехода. Как показано на рис. 7.9, его можно описать с помощью условных вероятностей.

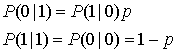(7.5)

Вероятность того, что выходной символ будет отличаться от входного, равна р, а вероятность того, что выходной символ будет идентичен входному, равна (1 -р). Канал BSC является примером канала с жесткой схемой принятия решений; это, в свою очередь, означает, что даже если демодулятор получил сигнал с непрерывным значением, BSC позволяет принять только какое-то одно определенное решение, так что каждый символ на выходе демодулятора, как показано на рис. 7.1, содержит одно из двух двоичных значений. Индексы величины указывают на j-й кодовый символ i-го ответвленного слова . Далее демодулятор передает последовательность Z={Z,} на декодер.

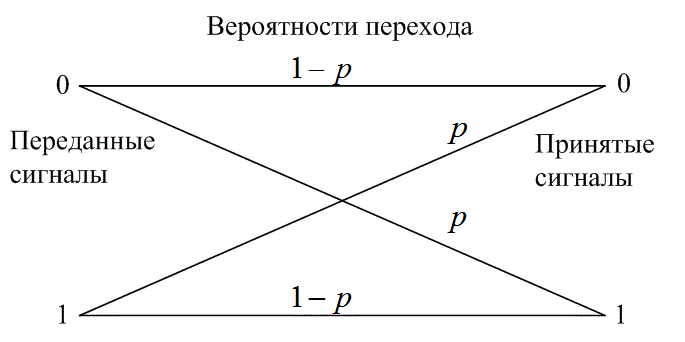
Рис. 7.9. Двоичный симметричный канал (канал с жесткой схемой принятия решений)

Пусть — это переданное по каналу BSC кодовое слово с вероятностью появления ошибочного символа р, Z - соответствующая последовательность, полученная декодером. Как отмечалось ранее, декодер, работающий по принципу максимального правдоподобия, выбирает кодовое слово , имеющее максимальное правдоподобие или его логарифм. Для BSC это эквивалентно выбору кодового слова находящегося на наименьшем расстоянии Хэмминга от Z [8]. Расстояние Хэмминга — это удобная метрика для описания расстояния или степени сходства между и Z. Из всех возможных переданных последовательностей декодер выбирает такую последовательность , для которой расстояние до Z минимально. Предположим, что каждая из последовательностей и Z имеет длину L бит и отличается на dm позиций (т.е. расстояние Хэмминга между и Z равно dm). Тогда, поскольку предполагалось, что канал не имеет памяти, вероятность того, что преобразовалось в Z, находящееся на расстоянии dm от может быть записана в следующем виде.

(7.6)

Логарифмическая функция правдоподобия будет иметь следующий вид.

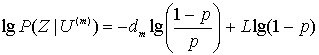(7.7)

Если вычислить эту величину для каждой возможно переданной последовательности, последнее слагаемое в уравнении будет постоянным для всех случаев. Если предположить, что , уравнение (7.7) можно записать в следующей форме.

(7.8)

Здесь А и В — положительные константы. Следовательно, такой выбор кодового слова , чтобы расстояние Хэмминга до полученной последовательности Z было минимальным, соответствует максимизации метрики правдоподобия или логарифма правдоподобия. Следовательно, в канале BSC метрика логарифма правдоподобия легко заменяется расстоянием Хэмминга, а декодер, работающий по принципу максимального правдоподобия, будет выбирать на древовидной или решетчатой диаграмме путь, соответствующий минимальному расстоянию Хэмминга между последовательностью и полученной последовательностью Z.

7.3.2.2. Гауссов канал

Для гауссова канала каждый выходной символ демодулятора , как показано на рис. 7.1, принимает значения из непрерывного алфавита. Символ нельзя пометить для обнаружения как правильное или неправильное решение. Передачу на декодер таких мягких решений можно рассматривать как поступление семейства условных вероятностей различных символов (см. раздел 6.3.1). Можно показать [8], что максимизация эквивалентна максимизации скалярного произведения последовательности кодовых слов (состоящей из двоичных символов, представленных как биполярные значения) и аналогового значения полученной последовательности Z. Таким образом, декодер выбирает кодовое слово , если выражение

(7-9)

имеет максимальное значение. Это эквивалентно выбору кодового слова , находящегося на ближайшем евклидовом кодовом расстоянии от Z. Даже несмотря на то что каналы с жестким и мягким принятием решений требуют различных метрик, концепция выбора кодового слова , ближайшего к полученной последовательности Z, одинакова для обоих случаев. Чтобы в уравнении (7.9) точно выполнить максимизацию, декодер должен осуществлять арифметические операции с аналоговыми величинами. Это непрактично, поскольку обычно декодеры являются цифровыми. Таким образом, необходимо дискретизировать полученные символы .He напоминает ли вам уравнение (7.9) демодуляционную обработку, рассмотренную в главах 3 и 4? Уравнение (7.9) является дискретным вариантом корреляции входного полученного сигнала с опорным сигналом , которая выражается уравнением (4.15). Квантованный гауссов канал, обычно называемый каналом с мягкой схемой решений, — это модель канала, в которой предполагается, что декодирование осуществляется на основе описанной ранее мягкой схемы принятия решения.

7.3.3. Алгоритм сверточного декодирования Витерби

Алгоритм декодирования Витерби был открыт и проанализирован Витерби (Viterbi) . [13] в 1967 году. В алгоритме Витерби, по сути, реализуется декодирование, основанное на принципе максимального правдоподобия; однако в нем уменьшается вычислительная нагрузка за счет использования особенностей структуры конкретной решетки кода. Преимущество декодирования Витерби, по сравнению с декодированием по методу "грубой силы", заключается в том, что сложность декодера Витерби не является функцией количества символов в последовательности кодовых слов. Алгоритм включает в себя вычисление меры подобия (или расстояния), между сигналом, полученным в момент времени , и всеми путями решетки, входящими в каждое состояние в момент времени . В алгоритме Витерби не рассматриваются те пути решетки, которые, согласно принципу максимального правдоподобия, заведомо не могут быть оптимальными. Если в одно и то же состояние входят два пути, выбирается тот, который имеет лучшую метрику; такой путь называется выживающим. Отбор выживающих путей выполняется для каждого состояния. Таким образом, декодер углубляется в решетку, принимая решения путем исключения менее вероятных путей. Предварительный отказ от маловероятных путей упрощает процесс декодирования. В 1969 году Омура (Omura) [14] показал, что алгоритм Витерби — это, фактически, максимальное правдоподобие. Отметим, что задачу отбора оптимальных путей можно выразить как выбор кодового слова с максимальной метрикой правдоподобия или минимальной метрикой расстояния.

7.3.4. Пример сверточного декодирования Витерби

Для простоты предположим, что мы имеем дело с каналом BSC; в таком случае приемлемой мерой расстояния будет расстояние Хэмминга. Кодер для этого примера показан на рис. 7.3, а решетчатая диаграмма — на рис. 7.7. Для представления декодера, как показано на рис. 7.10, можно воспользоваться подобной решеткой. Мы начинаем в момент времени в состоянии 00 (вследствие очистки кодера между сообщениями декодер находится в начальном состоянии). Поскольку в этом примере возможны только два перехода, начинающиеся в некотором состоянии, для начала не нужно показывать все ветви. Полная решетчатая структура образуется после момента времени . Принцип работы происходящего после процедуры декодирования можно понять, изучив решетку кодера на рис. 7.7 и решетку декодера, показанную на рис. 7.10. Для решетки декодера каждую ветвь за каждый временной интервал удобно пометить расстоянием Хэмминга между полученным кодовым символом и ответвляющимся словом, соответствующим той же ветви из решетки кодера. На рис. 7.10 показана последовательность сообщений m, соответствующая последовательности кодовых слов U, и исаженная шумом последовательность Z= 11 01 01 1001 — Как показано на рис. 7.3, кодер характеризуется кодовыми словами, находящимися на ветвях решетки кодера и заведомо известными как кодеру, так и декодеру. Эти ответвляющиеся слова являются кодовыми символами, которые можно было бы ожидать на выходе кодера в результате каждого перехода между состояниями. Пометки на ветвях решетки декодера накапливаются декодером в процессе. Другими словами, когда получен кодовый символ, каждая ветвь решетки декодера помечена метрикой подобия (расстоянием Хэмминга) между полученным кодовым символом и каждым ответвляющимся словом за этот временной интервал. Из полученной последовательности Z, показанной на рис. 7.10, можно видеть, что кодовые символы, полученные в (следующий) момент времени , — это 11. Чтобы пометить ветви декодера подходящей метрикой расстояния Хэмминга в (прошедший) момент времени , рассмотрим решетку кодера на рис. 7.7. Видим, что переход между состояниями 00 00 порождает на выходе ответвляющееся слово 00. Однако получено 11. Следовательно, на решетке декодера помечаем переход между состояниями 00 00 расстоянием Хэмминга между ними, а именно 2. Глядя вновь на решетку кодера, видим, что переход между состояниями 00 10 порождает на выходе ответвляющееся слово 11, точно соответствующее полученному в момент кодовому символу. Следовательно, переход на решетке декодера между состояниями 00 10 помечаем расстоянием Хэмминга 0. В итоге, метрика входящих в решетку декодера ветвей описывает разницу (расстояние) между тем, что было получено, и тем, что "могло бы быть" получено, имея ответвленные слова, связанные с теми ветвями, с которых они были переданы. По сути, эти метрики описывают величину, подобную корреляциям между полученным ответвляющимся словом и каждым из кандидатов на роль ответвляющегося слова. Таким же образом продолжаем помечать ветви решетки декодера по мере получения символов в каждый момент времени . В алгоритме декодирования эти метрики расстояния Хэмминга используются для нахождения наиболее вероятного (с минимальным расстоянием) пути через решетку.

Смысл декодирования Витерби заключается в следующем. Если любые два пути сливаются в одном состоянии, то при поиске оптимального пути один из них всегда можно исключить. Например, на рис. 7.11 показано два пути, сливающихся в момент времени в состоянии 00.

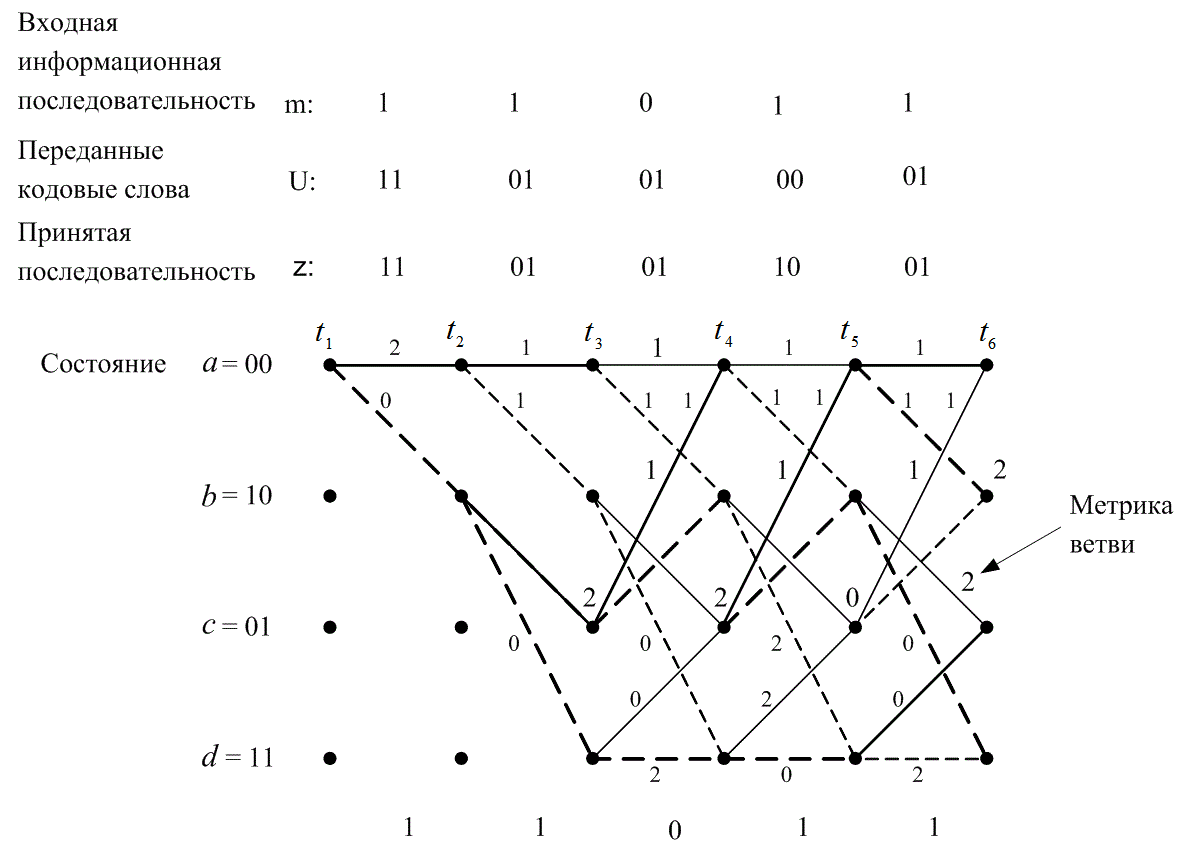
Рис. 7.10. Решетчатая диаграмма декодера (степень кодирования 1/2, K= 3)

Давайте определим суммарную метрику пути по Хэммингу для данного пути в момент времени , как сумму метрик расстояний Хэмминга ветвей, по которым проходит путь до момента ,. На рис. 7.11 верхний путь имеет метрику 4, нижний — метрику 1. Верхний путь нельзя выделить как оптимальный, поскольку нижний путь, входящий в то же состояние, имеет меньшую метрику. Это наблюдение поддерживается Марковской природой состояний кодера. Настоящее состояние завершает историю кодера в том смысле, что предыдущие состояния не могут повлиять на будущие состояния или будущие ветви на выходе.

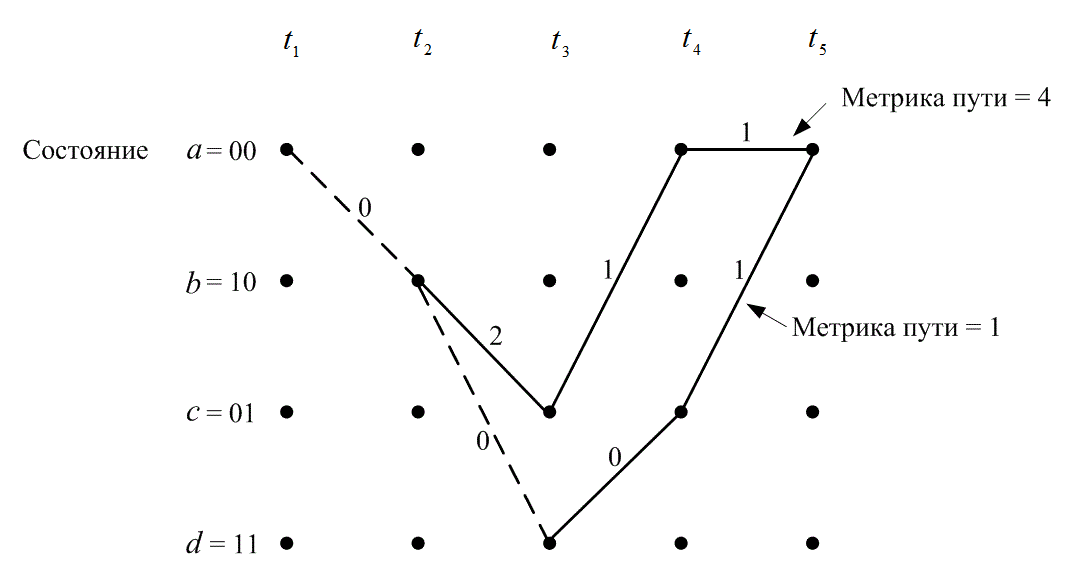
Рис. 7.11. Метрики пути для двух сливающихся путей

В каждый момент времени в решетке существует состояний, где K — это длина кодового ограничения, и в каждое состояние может войти два пути. Декодирование Витерби состоит в вычислении метрики двух путей, входящих в каждое состояние, и исключении одного из них. Такие вычисления проводятся для каждого из состояний или узлов в момент времени ; затем декодер переходит к моменту времени , и процесс повторяется. В данный момент времени метрика выжившего пути для каждого состояния обозначается как метрика для этого состояния в этот момент времени. Первые несколько шагов в нашем примере декодирования будут следующими (рис. 7.12). Предположим, что последовательность входящих данных т, кодовое слово U и Полученная последовательность Z аналогичны показанным на рис. 7.10. Допустим, что декодер знает верное исходное состояние решетки. (Это предположение не является необходимым, однако упрощает объяснения.) В момент времени получены кодовые символы 11. Из состояния 00 можно перейти только в состояние 00 или 10, как показано на рис. 7.12, а. Переход между состояниями 00 10 имеет метрику ветви 0; переход между состояниями 00 00 — метрику ветви 2. В момент времени из каждого состояния также может выходить только две ветви, как показано на рис. 7.12, б. Суммарная метрика этих ветвей обозначена как метрика состояний , , и , соответствующих конечным состояниям. В момент времени на рис. 7.12, на опять есть две ветви, выходящие из каждого состояния. В результате имеется два пути, входящих в каждое состояние, в момент времени . Один из путей, входящих в каждое состояние, может быть исключен, а точнее — это путь, имеющий большую суммарную метрику пути. Если бы метрики двух входящих путей имели одинаковое значение, то путь, который будет исключаться, выбирался бы произвольно. Выживший путь в каждом состоянии показан на рис. 7.12, г. В этой точке процесса декодирования имеется только один выживший путь, который называется полной ветвью, между моментами времени и . Следовательно, декодер теперь может решить, что между моментами и произошел переход 00 10. Поскольку переход вызывается единичным входным битом, на выходе декодера первым битом будет единица. Здесь легко можно проследить процесс декодирования выживших ветвей, поскольку ветви решетки показаны пунктирными линиями для входных нулей и сплошной линией для входных единиц. Заметим, что первый бит не декодируется, пока вычисление метрики пути не пройдет далее вглубь решетки. Для обычного декодера такая задержка декодирования может оказаться раз в пять больше длины кодового ограничения в битах.

На каждом следующем шаге процесса декодирования всегда будет два пути для каждого состояния; после сравнения метрик путей один из них будет исключен. Этот шаг в процессе декодирования показан на рис. 7.12, д. В момент снова имеется по два входных пути для каждого состояния, и один путь из каждой пары подлежит исключению. Выжившие пути на момент показаны на рис. 7.12, е. Заметим, что в нашем примере мы еще не можем принять решения относительно второго входного информационного бита, поскольку еще остается два пути, исходящих в момент из состояния в узле 10. В момент времени на рис. 7.12, ж снова можем видеть структуру сливающихся путей, а на рис. 7.12, з — выжившие пути на момент . Здесь же, на рис. 7.12, з, на выходе декодера в качестве второго декодированного бита показана единица как итог единственного оставшегося пути между точками и . Аналогичным образом декодер продолжает углубляться в решетку и принимать решения, касающиеся информационных битов, устраняя все пути, кроме одного.

Отсекание (сходящихся путей) в решетке гарантирует, что у нас никогда не будет путей больше, чем состояний. В этом примере можно проверить, что после каждого отсекания (рис. 7.12, б—д) остается только 4 пути. Сравните это с попыткой применить "грубую силу" (без привлечения алгоритма Витерби) при использовании для получения последовательности принципа максимального правдоподобия. В этом случае число возможных путей (соответствующее возможным вариантам последовательности) является степенной функцией длины последовательности. Для двоичной последовательности кодовых слов с длиной ответвленных слов L имеется возможные последовательности.

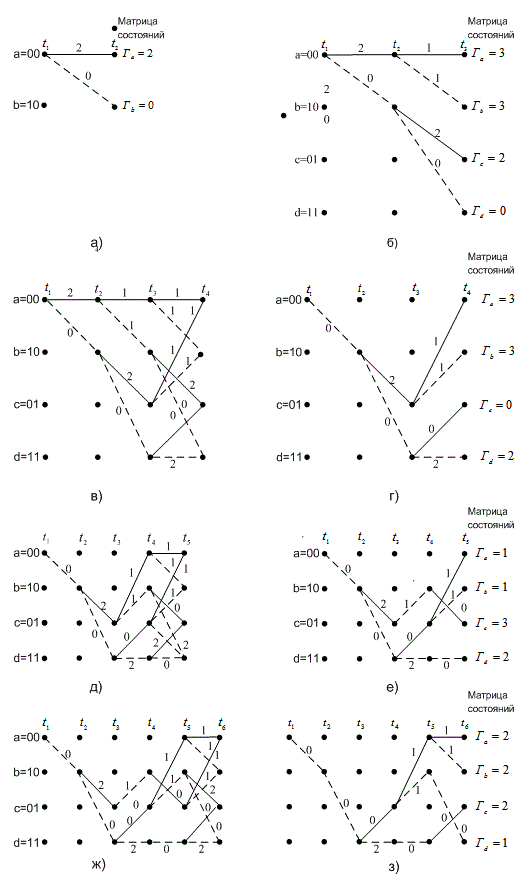
Рис. 7.12. Выбор выживших путей: а) выжившие на момент ; б) выжившие на момент ; в) сравнение метрик в момент ; г) выжившие на момент ; д) сравнение метрик в момент ; e) выжившие на момент ; ж) сравнение метрик в момент ; з) выжившие на момент

7.3.5. Реализация декодера

В контексте решетчатой диаграммы, показанной на рис. 7.10, переходы за один промежуток времени можно сгруппировать в непересекающиеся ячейки; каждая ячейка будет изображать четыре возможных перехода, причем называется памятью кодера (encoder memory). Если К = 3, то v = 2, и, следовательно, мы имеем ячейки. Эти ячейки показаны на рис. 7.13, где буквы a, b, c и d обозначают состояния в момент , а , , и —состояния в момент времени . Для каждого перехода изображена метрика ветви, индексы которой означают переход из состояния х в состояние у. Эти ячейки и соответствующие логические элементы, которые корректируют метрики состояний {}, где х означает конкретное состояние, представляют основные составляющие элементы декодера.

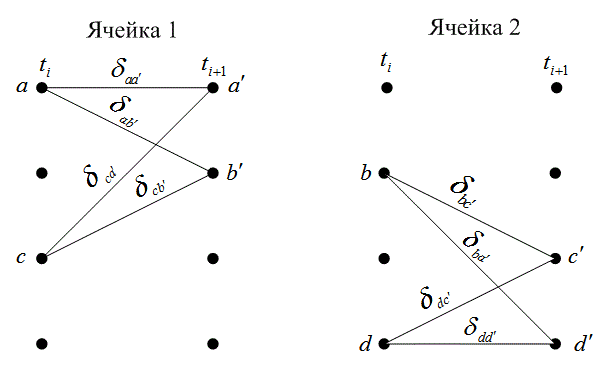
Рис. 7.13. Примеры ячеек декодера

7.3.5.1. Процедура сложения, сравнения и выбора

Вернемся к примеру двух ячеек с К = 3. На рис. 7.14 показан логический блок, соответствующий ячейке 1. Логическая схема осуществляет специальную операцию, которая называется сложение, сравнение и выбор (add-compare-select —ACS). Метрика состояния вычисляется путем прибавления метрики предыдущего состояния а, , к метрике ветви и метрики предыдущего состояния с, , к метрике ветви . Это даст в результате две метрики путей в качестве кандидатов для новой метрики состояния . Оба кандидата сравниваются в логическом блоке, показанном на рис. 7.14. Наиболее правдоподобная из двух метрик путей (с наименьшим расстоянием) запоминается как новая метрика состояния для состояния . Также сохраняется новая история путей . для состояния а, где — история пути информации для данного состояния, дополненная сведениями о выжившем пути.

На рис. 7.14 также показана логическая схема ACS для ячейки 1, которая дает новую метрику состояния и новую историю состояния . Операция ACS аналогичным образом осуществляется и для путей в других ячейках. Выход декодера составляют последние биты на путях с наименьшими метриками состояний.

7.3.5.2. Вид процедуры сложения, сравнения и выбора на решетке

Рассмотрим тот же пример, которым мы воспользовались в разделе 7.3.4 для описания декодирования на основе алгоритма Витерби. Последовательность сообщений имела вид m = 11011, последовательность кодовых слов — U=11 01 01 00 01, а принятая последовательность — Z=11 01 01 10 01.

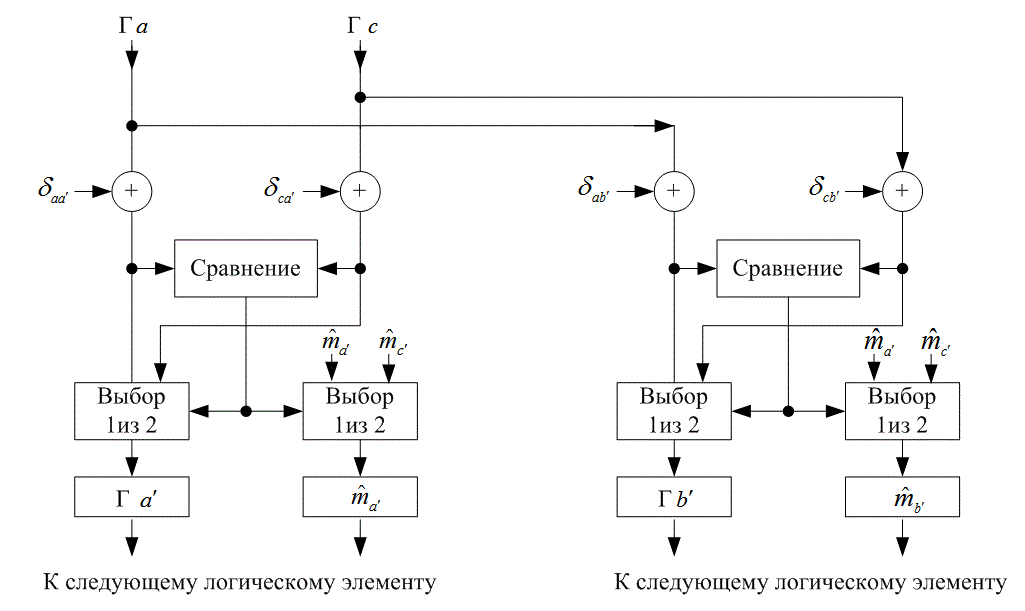
Рис. 7.14. Логический блок, предназначенный для осуществления операции сложения, сравнения и выбора

Решетчатая диаграмма декодирования, аналогичная показанной на рис. 7.10, изображена на рис. 7.15. Метрика ветви, которая описывает каждую ветвь, — это расстояние Хэмминга между принятым кодовым символом и соответствующим ответвленным словом из решетки кодера. Еще на решетке (рис. 7.15) показаны значения каждого состояния х в каждый момент , метрика состояния которых обозначена . Операция ACS выполняется после появления двух переходов, входящих в состояние, т.е. для момента и более поздних. Например, в момент времени значение метрики состояния для состояния а вычисляется суммированием метрики состояния = 3 в момент и метрики ветви , что в итоге дает значение 4. В то же время к метрике состояния в момент времени прибавляется метрика ветви , что дает значение 3. В ходе процедуры ACS происходит отбор наиболее правдоподобной метрики (с минимальным расстоянием), т.е. новой метрики состояния; поэтому для состояния а в момент новой метрикой состояния будет =3. Отобранный путь изображен жирной линией, а путь, который был отброшен, показан светлой линией. На рис. 7.15 на решетке слева направо показаны все метрики состояний. Убедимся, что в любой момент времени значение каждой метрики состояния получается суммированием метрики состояния, соединенного с предыдущим состоянием вдоль отобранного пути (жирная линия), и метрики ветви, соединяющей эти состояния. В определенной точке решетки (после временного интервала, равного 4 или 5 длинам кодового ограничения) будут декодированы самые ранние биты. Чтобы показать это, посмотрим на рис. 7.15 в момент . Видим, что значение метрики состояния, соответствующей минимальному расстоянию, равно 1. Отобранный путь можно проследить из состояния d обратно, к моменту , и убедиться, что декодированное сообщение совпадает с исходным. Напомним, что пунктирные и сплошные линии соответствуют двоичным единице и нулю.

7.3.6. Память путей и синхронизация

Требования к памяти декодера, работающего согласно алгоритму Витерби, растут с увеличением длины кодового ограничения как степенная функция. Для кода со степенью кодирования 1/n после каждого шага декодирования декодер держит в памяти набор из путей.

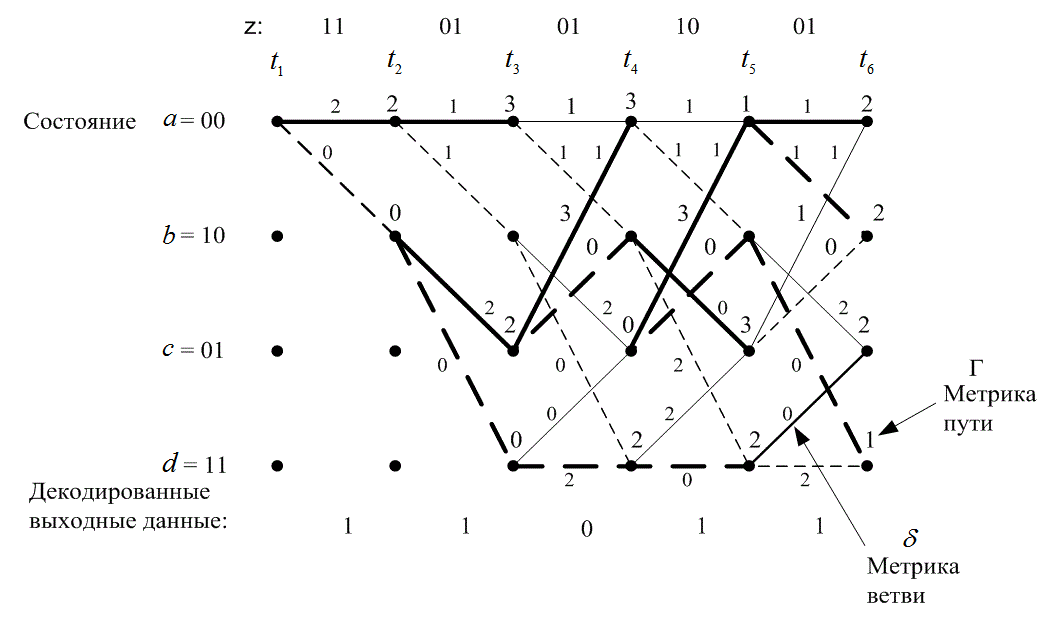
Рис. 7.15. Операция сложения, сравнения и выбора при декодировании по алгоритму Витерби

С высокой степенью вероятности при превышении существующей глубины декодирования эти пути не будут взаимно непересекающимися [12]. Все пути ведут к полной ветви, которая в конце концов разветвляется на разные состояния. Поэтому, если декодер сохраняет историю путей, самые первые биты на всех путях будут одинаковы. Следовательно, простой декодер имеет фиксированный объем истории путей и выдает самые ранние биты произвольного пути каждый раз, когда продвигается на один уровень вглубь решетки. Требуемый объем сохраняемых путей будет равен следующему [12].

(7.10)

Здесь h - длина истории пути информационного бита на состояние. При уточнении, которое проводится для минимизации h, вместо самых ранних битов произвольных путей на выходе декодера используются самые ранние биты наиболее вероятных путей. Было показано [12], что значения h, равного 4 или 5 длинам кодового ограничения, достаточно, чтобы характеристики декодера были близки к оптимальным. Необходимый объем памяти и является основным ограничением при разработке декодеров, работающих согласно алгоритму Витерби. В серийно выпускаемых декодерах длина кодового ограничения равна величине порядка К = 10. Попытка повысить эффективность кодирования за счет увеличения длины кодового ограничения вызывает степенной рост требований к памяти (и сложности), как это следует из уравнения (7.10).

Синхронизация ответвляющихся слов — это процесс определения начала ответвляющегося слова в принятой последовательности. Такую синхронизацию можно осуществить, не прибавляя новую информацию к потоку передаваемых символов, поскольку можно видеть, что, пока принятые данные не синхронизированы, у них непомерно высокая частота появления ошибок. Следовательно, синхронизацию можно осуществить просто: нужно проводить сопутствующее наблюдение за уровнем частоты появления ошибок, т.е. нас должна интересовать частота, при которой увеличиваются метрики состояний, или частота, при которой сливаются выжившие пути на решетке. Параметр, за которым следят, сравнивается с пороговым значением, после чего соответствующим образом осуществляется синхронизация.