Так же как и для преобразований Лапласа и Фурье, существуют теоремы для z-преобразования. Приведем наиболее важные теоремы одностороннего z-преобразования.

Теорема линейности (суперпозиции)

Сумме дискретных сигналов соответствует сумма их z-изображений. Если дискретным сигналам и соответствуют z-изображения и , то

,

где a и b - некоторые числа.

Доказательство теоремы выполните самостоятельно, используя выражение (13) для расчета z-изображения дискретного сигнала.

Теорема опережающего сдвига

Если дискретному сигналу соответствует одностороннее z-преобразование , то сигналу, сдвинутому на один интервал дискретизации, соответствует z-преобразование .

Математическая запись теоремы имеет вид

,

Чтобы доказать теорему, воспользуемся основным выражением (13) для расчета z-преобразования дискретных сигналов и , а также графиками, приведенными на рис. 23.

;

.

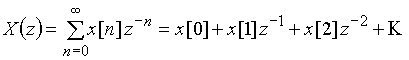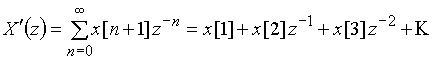Сравнивая и , получаем , что и требовалось доказать.

Очевидно, что теорема опережающего сдвига выполняет ту же самую роль, что и теорема дифференцирования для преобразований Лапласа.

Теорема задержки

Математическая запись теоремы имеет вид

.

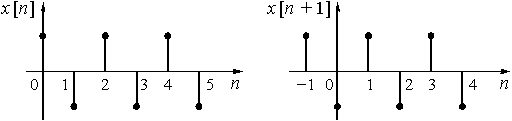
Рис. 23

В теореме задержки - это дискретные отсчеты функции единичного скачка (рис. 24)

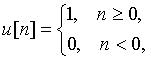
а - это дискретные отсчет функции , задержанной на N интервалов дискретизации (рис. 25).

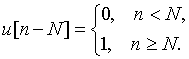
Доказательство вытекает из основного выражения (13) для z-преобразования.

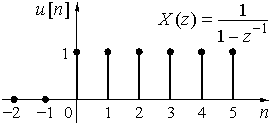
Рис. 24

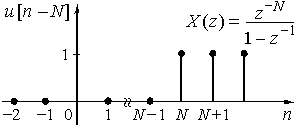
Рис. 25

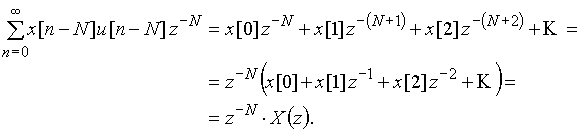
При доказательстве учтено, что единичная ступенчатая функция обращается в нуль при отрицательных значениях ее аргумента, т.е. при n < N.

Теорема умножения на aⁿ

Математическая запись теоремы имеет вид

.

Теорема умножения на n

.

Теоремы умножения дискретного сигнала на и на n можно также доказать, используя формулу (13). Предлагаем проделать это самостоятельно.

Теорема свертки

Свертке дискретных сигналов и соответствует произведение их z-преобразований

.

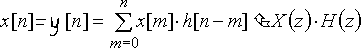Эту теорему мы приводим здесь без доказательства. При необходимости с ним можно познакомиться в [6].

Пример 11.1. Найдем z-преобразование функции единичного отсчета, задержанной на N интервалов дискретизации.

Найдем z-преобразование дискретного d-импульса (рис. 3), используя выражение (13)

.

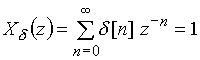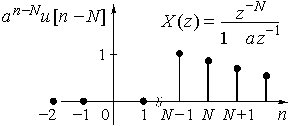
Рис. 26

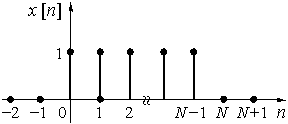
Рис. 27

Используя теорему задержки, найдем z-изображение сигнала

.

На рисунке 3 приведен также график задержанной функции единичного отсчета для частного случая N = 2.

Пример 11.2. Найдем z-преобразование функции

.

В примере 9.4 мы уже находили, что z-преобразование сигнала имеет вид (15) .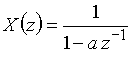

Используя теорему задержки, получаем

.

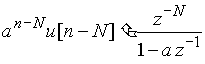При a = 1 имеем:

.

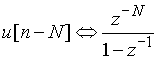Графики дискретных сигналов и приведены на рис. 25 и 26.

Пример 11.3. Найдем z-преобразование дискретной последовательности .

Поскольку z-изображение последовательности известно (15), то, используя теорему умножения на n, получим

.

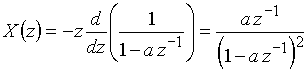Пример 11.4. Найдем z-преобразование дискретной последовательности из N отсчетов единичной амплитуды (рис. 27)

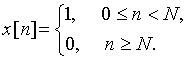
Сигнал можно представить как разность двух сигналов

.

Из теорем линейности и задержки легко получить z-преобразование

,

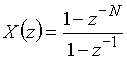что совпадает с формулой для частичной суммы геометрической прогрессии

.

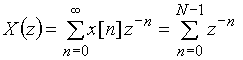Пример 11.5. Вычислим z-преобразование свертки дискретных сигналов ={1; 1; 1; 0; 0; 0; ...} и 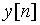= {0; 0; 1; 1; 0; 0; ...}.

Найдем z-преобразование сигнала , используя формулу (13)

.

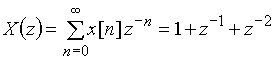Найдем z-преобразование сигнала

.

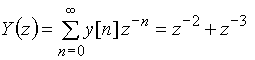Вычислим z-преобразование свертки сигналов и , используя теорему свертки

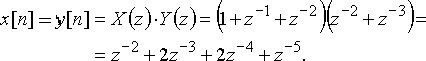
Табл. 1 - Краткая таблица односторонних z-преобразований

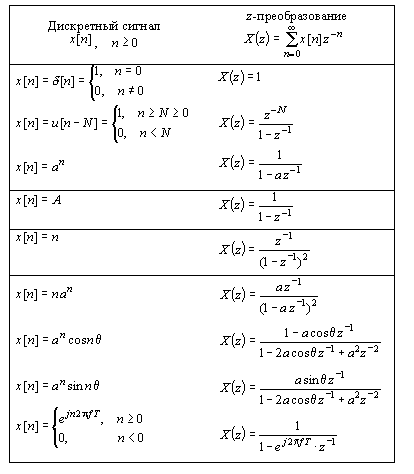
z-преобразование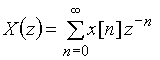

В табл. 1 дана сводка z-преобразований наиболее часто встречающихся дискретных последовательностей. Эти табличные сведения также могут быть использованы для расчета z-преобразований сигналов и перехода от z-преобразований к дискретным сигналам.

Пример 11.6. Найдем общий член дискретного сигнала , которому соответствует z-изображение

.

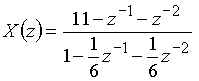Разложение функции на простые дроби приводит к выражению

.

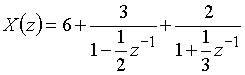Используя теорему линейности и находя в таблице 1 дискретные сигналы, соответствующие каждому из слагаемых в выражении , получаем

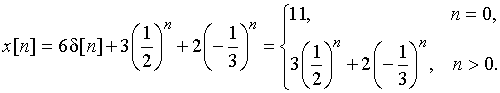
По этой формуле легко подсчитать значение для любого n. Аналогичным образом, разложение

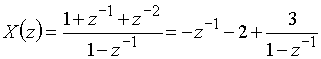
приводит к последовательности

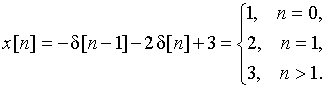
Самоконтроль

1. Докажите теорему линейности.

2. В чем суть теорем опережающего сдвига и задержки?

3. Сформулируйте теоремы умножения на и на n?

4. Как найти z-преобразование свертки дискретных сигналов?

5. Как можно использовать таблицу односторонних z-преобразований?