9.9.2. Границы совокупности сигналов
9.9.3. Совокупности сигналов высших размерностей
9.9.4. Решетчатые структуры высокой плотности
9.9.5. Комбинированная эффективность: отображение на N-мерную сферу и плотная решетка
Методы канального кодирования, описанные в главах 6-8, обычно не применяются в телефонных каналах (хотя первые испытания последовательного декодирования сверточных кодов проводились именно по телефонной линии). Недавно, однако, возник существенный интерес к методам, которые могут обеспечить эффективное кодирование в узкополосных каналах. Это связано с желанием получить надежную передачу по телефонным линиям при высоких скоростях передачи данных. Потенциальная эффективность составляет порядка 3 бит/символ (при данном отношении сигнал/шум) или, что то же самое, при данной вероятности ошибки можно достичь экономии мощности до 9 дБ [21].
Наибольший интерес представляют следующие три отдельные области исследования кодирования.
1. Оптимальные границы совокупностей сигналов (выбор наиболее плотно упакованного подмножества сигналов из любого регулярного массива или решетки возможных точек).
2. Структуры решеток с высокой плотностью (улучшение выбора подмножества сигналов за счет начала рассмотрения с наиболее плотной из возможных решеток пространства).
3. Решетчатое кодирование (комбинация методов модуляции и кодирования для получения эффективного кодирования в узкополосных каналах).
Первые две области не являются "истинными" схемами кодирования с защитой от ошибок. Под словами "истинная схема кодирования с защитой от ошибок" подразумевается метод, использующий некоторую структурную избыточность для снижения вероятности ошибки. Избыточность включает лишь третья позиция списка, решетчатое кодирование. Перечисленные области исследования кодирования и ожидаемые от них улучшения производительности обсуждаются ниже.
9.9.1. Коммерческие модемы
В использовании эффективных методов модуляции традиционно заинтересована телекоммуникационная индустрия, поскольку основные ресурсы телефонных компаний — это жестко ограниченные речевые (телефонные) каналы. Типичный телефонный канал характеризуется высоким отношением сигнал/шум (signal-to-noise ratio — SNR) порядка 30 дБ и полосой пропускания порядка 3 кГц. В табл. 9.4 представлена эволюция некоммутируемых телефонных модемов, и в табл. 9.5 — эволюция стандартов коммутируемых телефонных модемов.
9.9.2. Границы совокупности сигналов
Исследователи [22-26] изучили большое количество возможных совокупностей сигналов QAM, пытаясь найти структуру, которая снизит вероятность появления ошибок при данном среднем отношении сигнал/шум. На рис. 9.17 показано несколько примеров совокупностей символов для М = 4, 8 и 16, которые рассматривались в [22]. Циклические наборы обозначаются как (а, b, ...), где а — количество сигналов во внутреннем круге, b — сигналы следующего круга и т.д. В общем, правило совокупности, известное как правило построения Кампопьяно-Глейзера (Campopiano-Glazer) [24], которое дает оптимальные характеристики множества сигналов, можно сформулировать так: из бесконечного массива точек, плотно упакованных в регулярный массив или решетку, в качестве совокупности сигналов выбрать плотно упакованное подмножество 2k точек. В данном случае "оптимальный" означает среднюю минимальную среднюю или пиковую мощность при данной вероятности ошибки. В двухмерном пространстве сигналов оптимальная граница, окружающая массив точек, стремится к окружности. На рис. 9.18 показаны примеры 64-арной (k = 6) и 128-арной (fc = 7) совокупностей сигналов из прямоугольного массива. Крестообразные границы — это компромиссное представление оптимальной окружности. Совокупность k = 6 использована в модеме Paradyne 14,4 Кбит/с. По сравнению с квадратной, кольцевая граница дает улучшение характеристик всего на 0,2 дБ [21].
Таблица 9.4. Эволюция некоммутируемых телефонных модемов
|
Год |
Название |
Максимальная скорость передачи битов (бит/с) |
Скорость передачи сигналов (символов/с) |
Метод модуляции |
Эффективность передачи сигналов(бит/символ) |
|
1962 |
Bell 201 |
2400 |
1200 |
4-PSK |
2 |
|
1967 |
Milgo 4400/48 |
4800 |
1600 |
8-PSK |
3 |
|
1971 |
Codex 9600C |
9600 |
2400 |
16-QAM |
4 |
|
1980 |
Paradyne MP14400 |
14400 |
2400 |
64-QAM |
6 |
|
1981 |
Codex SP14.4 |
14400 |
2400 |
64-QAM |
6 |
|
1984 |
Codex 2660 |
16 800 |
2400 |
Решетчатая 256-QAM |
7 |
|
1985 |
Codex 2680 |
19200_ |
2743 |
8-D решетчатая 160-QAM |
7_ |
Таблица 9.5. Эволюция стандартов коммутируемых телефонных модемов
|
Год |
Название |
Максимальная скорость передачи битов (бит/с) |
Скорость передачи сигналов (символов/с) |
Метод модуляции |
Эффективность передачи сигналов(бит/символ) |
|
1984 |
V.32 |
9600 |
2400 |
2-D решетчатая 32-QAM |
4 |
|
1991 |
V.32bis |
14400 |
2400 |
2-D решетчатая 128-QAM |
6 |
|
1994 |
V.34 |
28 800 |
2400,2743,2800,3000,3200,3429 |
4-D решетчатая 960-QAM |
=9 |
|
1996 |
V.34 |
33 600 |
2400,2743,2800,3000,3200, 3429 |
4-D решетчатая 1664-QAM |
=10 |
|
1998 |
4.90 |
по направлению основного потока: - 56 000 против направления основного потока: - 33 600 |
8000 как в V.34 |
РСМ'(М-РАМ) как в V.34 |
7 =10 |
|
2000 |
V.92 |
по направлению основного потока: - 56 000 против направления основного потока: - 48 000 |
8000 8000 |
РСМ'(М-РАМ) Решетчатая РСМ |
7 6 |
Рис. 9.17. Совокупности М-арных символов. (Перепечатано с разрешения авторов из работы Thomas С. М., Weidner M. Y. and Durrani S. N. "Digital Amplitude-Phase Shift Keying with M-ary Alphabets," IEEE Trans. Commun., vol. COM22, n. 2, February, 1974, Figs. 2 and 3, p. 170. © 1974, IEEE.)
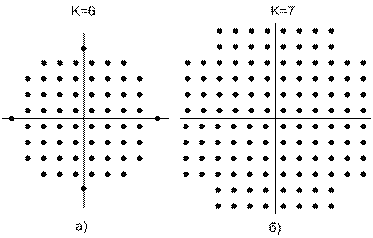
Рис. 9.18 Примеры М-арных совокупностей, использующих прямоугольную решетку.
9.9.3. Совокупности сигналов высших размерностей
Для любой скорости передачи информации и шумового процесса в канале, который независимо и одинаково распределен в двух измерениях, передача сигнала в двухмерном пространстве может дать такую же вероятность ошибки при меньшей средней (или пиковой) мощности, как и передача сигналов в одномерном импульсно-амплитудном (pulse-amplitude — РАМ) пространстве. Это выполняется посредством выбора точек сигналов на двухмерной решетке в пределах кольцевой, а не квадратной границы. Аналогичным образом, переходя к измерению высшей размерности N и выбирая точки на n-мерной решетке в пределах не N-мерного куба, а N-мерной сферы, можно еще больше сэкономить энергию [27-30]. Задачей подобного формирования совокупности является снижение требуемой средней энергии точек сигнала, расположенных внутри N-мерной сферы, по сравнению с энергией точек, расположенных внутри N-мерного куба. Такое снижение требуемой энергии при данной вероятности ошибки называется эффективностью выбора формы (shaping gain) [16]. В табл. 9.6 показано, как можно сэкономить энергию в N измерениях. Если устремить N к бесконечности, эффективность будет стремиться к 1,53 дБ; как правило, эффективность порядка 1 дБ получить нетрудно [16, 21].
Таблица 9.6. Экономия энергии при замене N-мерного куба N-мерной сферой (эффективность выбора формы)
|
Размерность (N) |
Эффективность (дБ) |
|
2 |
0,20 |
|
4 |
0,45 |
|
8 |
0,73 |
|
16 |
0,98 |
|
24 |
1,01 |
|
32 |
1,17 |
|
48 |
1,26 |
|
64 |
1,31 |
Источник: G. D. Forney, Jr., et. al. "Efficient Modulation for Bandlimited Channels," IEEE J. Set. Areas Commun., vol. SAC2, n. 5, September, 1984, pp. 632-647.
Канал, по сути, является двухмерным, поскольку символы, представленные на двухмерной плоскости в виде точек, передаются квадратурным образом. Многомерная передача сигналов обычно означает передачу с использованием двух или большего числа таких плоскостей. Для передачи п бит/символ при N-мерной (N четное и большее 2) передаче входящие биты группируются в блоки размером nN/2. Затем требуется выполнить отображение, при котором значения информационных битов присваиваются 2nN/2 N-мерным векторам, имеющим минимальную энергию среди всех векторов пространства. Соответствующее обратное отображение производится приемником.
Рассмотрим пример отображения сигналов из двухмерного пространства в четырехмерное. Сначала имеется двухмерная M-арная совокупность сигналов, например, M-QAM с М=16. Здесь переданный символ, рассматриваемый как точка на плоскости, представляется n=4 бит (две квадратурные амплитуды, по два бита на амплитуду). Каждая передача символа состоит из передачи вектора, принадлежащего пространству из 16 возможных векторов. При четырехмерной передаче сигналов переданный символ (рассматриваемый как две точки, по одной на каждой из двух плоскостей) представляется 8 бит. Тогда, каждая (двухточечная) передача состоит из передачи вектора из пространства 16 х 16 = 256 векторов. Вообще, исходные биты данных группируются в блоки размером nN/2 бит. В данном примере четырехмерной передачи сигналов информационные биты группируются в блоки из 8 бит (2 плоскости 
п= 4 бит/плоскость). Такую 8-битовую передачу можно рассматривать как отображение из пространства 2n двухмерных векторов в пространство 2nN/2 четырехмерных векторов. Для четырехмерной системы, изображенной на рис. 9.19, данный источник производит один из 256 четырехмерных векторов mi (i= 1, 2, ..., 256) путем группирования двух 16-ричных символов (двух плоскостей) за раз и передает сигналы аj х(t), bj s(t), Cj s(t), dj s(t), где j = 1, ..., 4 представляет одно 4-ричное значение амплитуды. Эти узкополосные или полосовые сигналы передаются по раздельным неинтерферирующим каналам. В каждом канале сигналы независимо искажаются AWGN, и в приемнике они демодулируются с помощью согласованных фильтров. Передавать УУ-мерный сигнал можно посредством следующих способов.
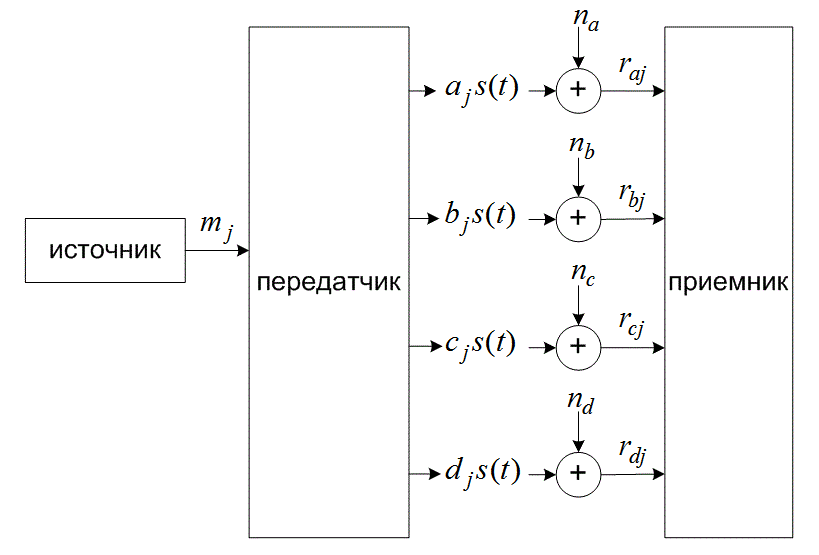
Рис. 9.19. Конфигурация четырехмерной системы
1. С помощью четырех отдельных проводников, представляющих четыре узкополосных канала.
2. С использованием двух полосовых каналов, в каждом из которых раздельно модулированы синфазный и квадратурный компоненты.
3. Путем уплотнения с частотным и временным разделением для создания нескольких узкополосных или полосовых каналов в общей линии передачи.
4. При помощи ортогональной поляризации электромагнитных волн.
Таким образом, если пример на рис. 9.19 представляет радиосистему, можно следовать методу 2 и квадратурным образом модулировать сигналы ajs(t) и bjs(t) на одной несущей, а сигналы сjs(t) и djs(t) — на другой. Таким образом, в течение каждого интервала, длительностью 2Т секунд, можно передать четыре 4-ричных числа, представляющих 8 бит или вектор из 256-ричного пространства. Дополнительной эффективности выбора формы можно достичь аналогичным образом при использовании 16-ричных символов на плоскости с шестимерной передачей сигналов, если передача 16-ричного символа со всех трех плоскостей происходит каждые ЗТ секунд. Таким образом, каждый шестимерный сигнал содержит три 16-ричные величины, представляющие 12 бит или точку в пространстве 4096 сигналов. Важно подчеркнуть, что это — не просто эффективная группировка 16-ричных символов. Эффективность проявляется вследствие того, что обнаружение, выполняемое в большем пространстве сигналов, может дать нужную достоверность передачи при более низком значении Eb|N0. При передаче 16-ричных символов с помощью шестимерной передачи сигналов каждые 3T секунд обнаруживается последовательность из 12 бит (не 4 бит за Т секунд!). Обнаружение в пространстве большей размерности требует более сложной реализации. В основном, уменьшение сложности отображения происходит за счет снижения эффективности использования энергии.
9.9.4. Решетчатые структуры высокой плотности
В разделе 9.9.3 описывался выбор плотно упакованного подмножества точек из регулярного массива или решетки. Здесь будет рассмотрено дополнительное улучшение, поэтому мы начнем с наиболее плотной решетки пространства. В двухмерном пространстве сигналов наиболее плотной решеткой является гексагональная (проверьте, пытаясь наиболее плотно уложить монеты на столе!). Результатом замены прямоугольной решетки, подобной показанным на рис. 9.18, на гексагональную является экономия средней энергии до 0,6 дБ. На рис. 9.20 показано несколько примеров гексагональной упаковки. Представленная на рис. 9.20, а совокупность была открыта Фоскини (Foschini) и др. [26] и является самым лучшим методом из известных 16-ричных размещений. Расположение точек, показанное на рис. 9.20, б, было использовано в модеме Codex SP14.4.
Рис. 9.20. Пример М-арных совокупностей с гексагональным расположением элементов
Гексагональная решетка является оптимальной для двух измерений. В пространствах более высоких размерностей имеются другие решетчатые структуры, которые дают наиболее плотную упаковку. В табл. 9.7 приводится улучшение (в децибелах), возникающее при переходе от применения прямоугольных решеток к лучшим из известных на настоящее время способам плотной упаковки.
Таблица 9.7. Экономия энергии при плотной решетке по сравнению с прямоугольной
|
Размерность (N) |
Эффективность плотной решетки (дБ) |
|
2 |
0,62 |
|
4 |
1,51 |
|
8 |
3,01 |
|
16 |
4,52 |
|
24 |
6,02 |
|
32 |
6,02 |
|
48 |
7,78 |
|
64 |
8,09 |
Источник: G. D. Forney, Jr., et. al. "Efficient Modulation for Bandlimited Channels," IEEE J. Sel. Areas Commun., vol. SAC2, n. 5, September, 1984, pp. 632-647.
9.9.5. Комбинированная эффективность: отображение на N-мерную сферу и плотная решетка
Преимущества границы Кампопьяно-Глейзера в N измерениях можно объединить с преимуществами наиболее плотной решетки в N-мерном пространстве. Суммарный выигрыш — это комбинация выигрыша N -мерной сферы по сравнению с N -мерным кубом (табл. 9.6) и преимущества плотной упаковки решетки (табл. 9.7). Экономия энергии, получаемая в результате такого объединения, представлена в табл. 9.8.
Таблица 9.8. Суммарная экономия энергии при использовании максимально плотной решетки и замене N -мерного куба N-мерной сферой
|
Размерность (N) |
Экономия энергии (дБ) |
|
2 |
0,82 |
|
4 |
1,96 |
|
8 |
3,74 |
|
16 |
5,50 |
|
24 |
7,12 |
|
32 |
7,19 |
|
48 |
9,04 |
|
64 |
9,40 |
Источник: G. D. Forney, Jr., et. al. "Efficient Modulation for Bandlimited Channels," IEEE J. Sel. Areas Commun., vol. SAC2, n. 5, September, 1984, pp. 632-647.