Постановка задачи анализа

Пусть к нелинейному резистивному элементу подведено гармоническое колебание и постоянное напряжение смещения U₀, т. е. пусть . Ток в элементе может быть найден по вольт-амперной характеристике элемента i = F(u) и является функцией времени i(t).

График тока i(t) может быть найден с помощью простейших построений, которые иллюстрируются на рис. 11.7. Данные этого рисунка показывают, что реакция i(t) и воздействие u(t) могут существенно отличаться по форме.

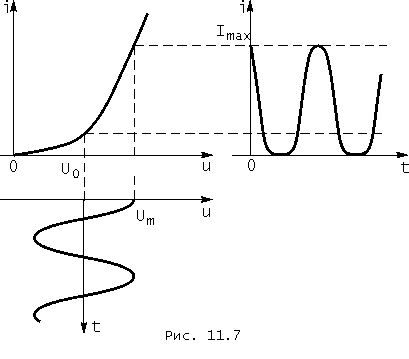
Искажения формы сигнала, обусловленные нелинейностью характеристик электрической цепи, называются нелинейными искажениями.

При воздействии , подведенном к нелинейному элементу, ток i(t) в элементе будет периодической функцией времени, которая может быть представлена рядом Фурье в форме (5.9) :

.

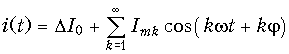Следовательно, ток в нелинейном элементе содержит постоянную составляющую D I₀, гармоническое колебание с частотой w и начальной фазой j воздействия и гармонические колебания с частотами, кратными частоте воздействия (гармоники колебания). Начальные фазы гармоник кратны начальной фазе воздействия.

Появление гармоник в составе тока в элементе обусловлено нелинейностью его вольт-амперной характеристики, в связи с чем их часто называют продуктами нелинейности.

В соответствии с изложенным спектр амплитуд тока в нелинейном элементе при гармоническом воздействии на элемент является дискретным. Такими же будут спектры напряжений и токов в тех ветвях цепи, которые не подсоединены непосредственно к источнику гармонического воздействия.

В устройствах, используемых в режиме малого сигнала, нелинейные искажения носят паразитный характер и строго нормируются. Для их оценки обычно используется коэффициент нелинейности

,

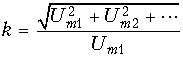где U_m1 – амплитуда колебания основной частоты (частоты воздействия), a U_m2, U_m3, ... – амплитуды гармоник напряжения на выходных зажимах устройства. Так, в высококачественных системах звуковоспроизведения коэффициент нелинейности не превышает долей одного процента.

Ниже рассматриваются аналитические методы вычисления спектров амплитуд колебаний в нелинейных резистивных электрических цепях для различных функций, аппроксимирующих вольт-амперную характеристику нелинейного элемента.

Спектр реакции при полиномиальной характеристике нелинейного элемента

Пусть в окрестности рабочей точки (U₀, I₀) вольт-амперная характеристика нелинейного элемента описывается полиномом степени n:

При гармоническом воздействии, когда ,

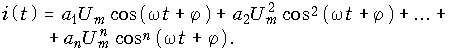
Для нахождения спектра амплитуд реакции тока i(t) в нелинейном элементе удобно вместо общего метода разложения периодической функции i(t) в ряд Фурье воспользоваться выражениями степеней функции cos^ka через функции кратных дуг, согласно которым:

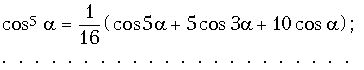
Тогда, полагая и осуществляя группировку коэффициентов при функциях одинаковых аргументов, преобразуем выражение для i(t) к виду

где:

Анализ полученных выражений показывает, что при полиномиальной вольт-амперной характеристике нелинейного элемента и гармоническом воздействии на НЭ:

1. Число гармонических составляющих реакции (гармоник) конечно и равно степени полинома, поскольку при n > 2:

2. Амплитуда I_m1 первой гармоники колебания при n > 2 в общем случае нелинейно зависит от амплитуды U_mприложенного воздействия.
3. Амплитуды четных (нечетных) гармоник определяются только коэффициентами при четных (нечетных) степенях слагаемых полинома.
4. Изменяется на величину D I₀ постоянная составляющая тока.

Спектр реакции при линейно-ломаной характеристике нелинейного элемента

Пусть на одном из участков ВАХ нелинейного элемента монотонно возрастает по закону, близкому к линейному, а на другом, когда элемент "заперт", может считаться равной нулю. Пусть, далее, между ними расположен небольшой по сравнению с первым участок, в котором одна из указанных характеристик переходит в другую. Примером может служить усредненная анодно-сеточная характеристика мощного пентода, приведенная на рис. 11.8, где i_А – анодный ток; u_СК – напряжение между сеткой и катодом. Пусть, наконец, мгновенные значения напряжения на выходе нелинейного элемента изменяются в пределах всех трех участков его характеристики.

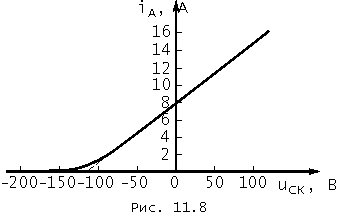
При сформулированных условиях рассматриваемую нелинейную характеристику можно и целесообразно аппроксимировать линейно-ломаной зависимостью, изображенной на рис. 10.32, б. Напряжение "излома" этой зависимости U_отс находится обычно как точка пересечения обоих линейных участков характеристики. Так, на рис. 11.8 U_отс = - 120 В.

Решим задачу спектрального анализа колебаний в нелинейном элементе с рассматриваемой линейно-ломаной вольт-амперной характеристикой, если ко входу элемента подведено напряжение . Закон изменения тока в элементе может быть, как и ранее, найден с помощью графических построений. Они приведены на рис. 11.9 и показывают, что искомый ток представляет собой периодическую последовательность импульсов, отличающихся от нуля в интервалах (k = 0, ±1; ±2; ...).

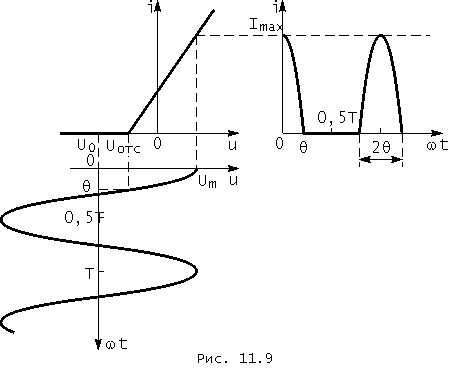
Форма одиночного импульса в интервале описывается в обозначениях рис. 11.9, как легко убедиться, функцией

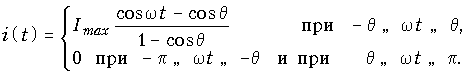
Действительно, при w t = 0 ток i(0) = I_max, при w t = ±q i(t) = = 0, а в интервале функция i(t) изменяется как ограниченная снизу (отсеченная) косинусоида.

Угол q называется углом отсечки. При гармоническом воздействии угол отсечки определяет в интервале нижнюю (w t = - q ) и верхнюю (w t = q ) границы временного интервала, в котором ток в элементе отличен от нуля. Поскольку на границах интервала (см. рис. 11.9), то

.

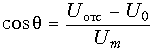Пределы изменения угла отсечки заключены между q = 0, когда нелинейный элемент заперт, и q = p (q = 180° ), когда ограничение снизу отсутствует, т. е. когда элемент используется в линейном режиме.

Для нахождения спектра амплитуд рассматриваемой периодической последовательности разложим ее в ряд Фурье. Тогда, опуская промежуточные выкладки, находим следующие выражения:

для постоянной составляющей тока

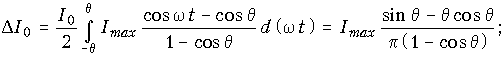(11.5, а)

для амплитуды первой (основной) гармоники

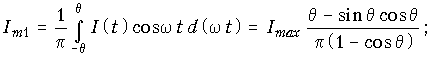
(11.5, б)

для второй гармоники

(11.5, в)

Эти выражения можно было бы получить как частные случаи существующей общей формулы для амплитуды k-й гармоники

На рис. 11.10 приведены графики тока и спектра амплитуд тока, соответствующие углу отсечки q = p /3.

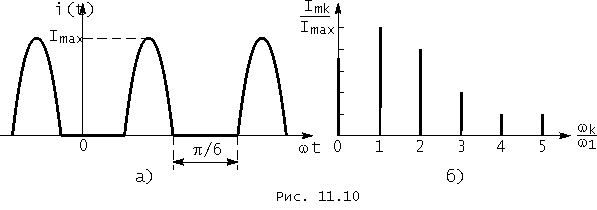
Постоянная составляющая и амплитуды гармоник тока в элементе являются функциями угла отсечки. Обычно они выражаются в относительных единицах

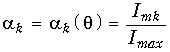
и называются коэффициентами А.И. Берга. Их графики приведены на рис. 11.11 для k Ф 3.

Анализ установленных соотношений показывает, что при линейно-ломаной характеристике нелинейного элемента и гармоническом воздействии на него:

1. Число гармонических составляющих реакции бесконечно велико, хотя амплитуды некоторых из них при определенных значениях угла отсечки могут быть равны нулю.
2. В общем случае амплитуды гармоник нелинейно зависят от амплитуды гармонического воздействия в силу нелинейного характера зависимости угла отсечки от U_m.
3. В частном случае, когда рабочая точка U₀ совмещена с точкой излома характеристики U_отс, т. е. когда угол отсечки равен p /2, амплитуды гармоник оказываются прямо пропорциональными амплитуде U_m гармонического воздействия, поскольку при этом условии величина I_max прямо пропорциональна U_m, а угол отсечки согласно (11.4) не изменяется с изменением U_m.

Выражение (11.6) является достаточно громоздким для выполнения вычислений. Из (11.7) следует, что

Выражая величину I_max через амплитуду U_m напряжения на НЭ, крутизну S вольт-амперной характеристики и угол отсечки q

получим более компактную формулу для расчета амплитуд гармоник тока:

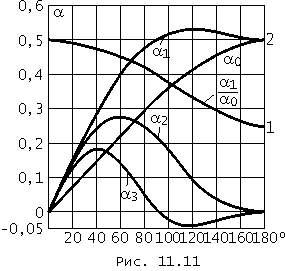
где – функции Берга.

Графики нескольких таких функций представлены на рис. 11.12.

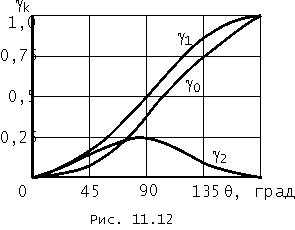
Пример. Считая, что диод обладает идеализированной характеристикой, определить U₀, при котором в спектре напряжения U_R(t) отсутствует 3-я гармоника, если (рис. 11.13, а).

Напряжение на сопротивлении R создают гармоники тока. Выражение для амплитуды k-той гармоники тока при кусочно-линейной аппроксимации НЭ имеет вид (11.6):

Приравнивая в этом выражении амплитуду 3-й гармоники нулю I_m3 = 0, получим

Учитывая, что

перепишем (11.9) в виде

Учитывая, что , получим

;

; ; ,

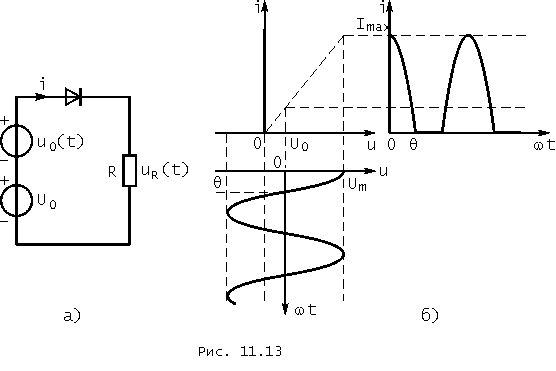
что выполняется при (рис. 11.13, б).