Внутри волновых пакетов отдельные волны распространяются с различными скоростями благодаря их различным длинам. Скорость распространения такого волнового пакета называется групповой скоростью. Определен и соответствующий групповой показатель преломления ng, который соотносится с показателем преломления следующим образом
ng = n –l 
. (2.4.1)
На рисунке 2.5 показаны кривые для n и ng для чистого кварцевого стекла в зависимости от длины волны l.
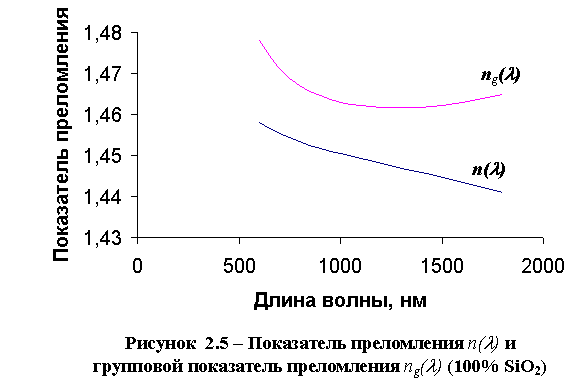
В таблице 2.1 представлены некоторые численные значения n(l) и ng(l) для кварца.
Таблица 2.1 – Показатель преломления n(l) и групповой показатель преломления ng(l)
|
Длина волны l, нм |
Показатель преломления n |
Групповой показатель преломления ng |
|
600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 |
1,4580 1,4553 1,4533 1,4518 1,4504 1,4492 1,4481 1,4469 1,4458 1,4446 1,4434 1,4422 1,4409 |
1,4780 1,4712 1,4671 1,4646 1,4630 1,4621 1,4617 1,4616 1,4618 1,4623 1,4629 1,4638 1,4648 |
Выражение dn/dl дает наклон кривой показателя преломления n(l), который в рассматриваемом диапазоне длин волн является нисходящим (отрицательным). Поэтому групповой показатель преломления ng при любой длине волны больше показателя преломления n. Для расчетов времени передачи оптических сигналов следует использовать только групповой показатель преломления ng.
Полезно отметить, что групповой показатель преломления достигает своего минимума вблизи длины волны 1300 нм. Этот диапазон длин волн является особенно интересным для оптической связи.
Если рассматривать показатель преломления n волоконного световода как функцию от радиуса r, то используется термин профиль распределения показателя преломления. С его помощью описывается радиальное изменение показателя преломления от оси волокна в стекле сердцевины в направлении стекла оболочки: n=n(r).
Распределение мод в волоконном световоде зависит от формы этого профиля распределения показателя преломления (рисунок 2.6).
Для практического применения важными являются «профили распределения показателя преломления, описываемые по степенному закону» (степенные профили). Под ними понимаются профили показателя преломления, у которых кривая изменения по радиусу описывается как степенная функция радиуса:
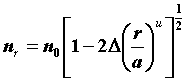, для r < a (в сердцевине) (2.4.2)
и
n2(r)=n22 = постоянная , для r ³ a (в оболочке) (2.4.3)
где
n0 - показатель преломления в центре сердцевины;
n1 - показатель преломления вдоль оси оптического волокна;
D - нормированная разность показателей преломления;
r - расстояние от оси оптического волокна, мкм;
a - радиус сердцевины, мкм;
u - показатель степени профиля;
n2 - показатель преломления оболочки.
Нормированная разность показателей преломления соотносится с числовой апертурой NA или показателями преломления n1 и n2 следующим образом
D = (NA)2 / 2 n21 = (n21 - n22) / 2 n21 . (2.4.4)
Отметим особые случаи (рисунок 2.6):
u = 1 – треугольный профиль
u = 2 – параболический профиль
u ®¥ – ступенчатый профиль (предел величины u - бесконечность).
Лишь в последнем случае – при ступенчатом профиле – показатель преломления n(r)=n1 в стекле сердцевины остается постоянным. Для всех других профилей показатель преломления n(r) в стекле сердцевины постепенно увеличивается от n2 для стекла оболочки до n1 у оси волоконного световода.
Поэтому такие профили называют градиентными профилями распределения показателя преломления. Это название особенно хорошо закрепилось за параболическим профилем, имеющим u=2, оптические волокна с таким профилем имеют технически очень хорошие характеристики передачи света.