При передаче непрерывных сообщений переданные сигналы s(t) являются функциями времени, принадлежащими некоторому множеству, а принятые сигналы x(t) будут их искаженными вариантами. Все реальные сигналы имеют спектры, основная энергия которых сосредоточена в ограниченной полосе F. Согласно теореме Котельникова такие сигналы определяются своими значениями в точках отсчета, выбираемых через интервалы . В канале на сигнал накладываются помехи, вследствие чего количество различимых уровней сигнала в точках отсчета будет конечным. Следовательно, совокупность значений непрерывного сигнала эквивалентна некоторой дискретной конечной совокупности. Это позволяет нам определить необходимое количество информации и пропускную способность канала при передаче непрерывных сообщений на основании результатов, полученных для дискретных сообщений.

Определим сначала количество информации, которое содержится в одном отсчете сигнала. относительно переданного сигнала. Это можно сделать на основании соотношения (6.41), если в последнем вероятности выразить через соответствующие плотности вероятности и взять предел при

(6.67)

Среднее количество информации в одном отсчете непрерывного сигнала определяется путем усреднения выражения (6.67) по всем значениям s и x:

(6.68)

где p(s, x) — совместная плотность вероятности, а S и X — области возможных значений s и х.

Выражение (6.68) можно представить как разность

(6.69)

где

(6.70)

Величина H(s) характеризует информационные свойства сигналов и по форме записи аналогична энтропии дискретных сообщений (6.6). Так как в выражение (6.70) входит дифференциальное распределение вероятностей p(s), то H(s) называют дифференциальной энтропией сигнала s. Выражение H(s/x) представляет собой условную дифференциальную энтропию сигнала s:

(6.71) Подобно тому, как это было сделано для дискретного канала, выражение (6.68) можно записать в другой форме

(6.72)

где

(6.73)

— дифференциальная энтропия сигнала х и

(6.74)

— условная дифференциальная энтропия сигнала х, называемая также энтропией шума.

Многие свойства энтропии непрерывного распределения аналогичны свойствам энтропии дискретного распределения. Если непрерывный сигнал s ограничен интервалом то энтропия H(s) максимальна и равна log(), когда сигнал 5 имеет равномерное распределение

(6.75)

Если ограничено среднеквадратичное значение непрерывного сигнала

то энтропия, максимальная при нормальном распределении,

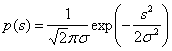(6.76)

и равна:

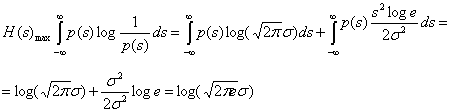(6.77)

Необходимо отметить, что, в отличие от энтропии дискретных сигналов, величина дифференциальной энтропии зависит от размерности непрерывного сигнала. По этой причине она не является мерой количества информации, хотя и характеризует степень неопределенности, присущую источнику. Только разность дифференциальных энтропии (6.69) или (6.72) количественно определяет среднюю информацию