Для того чтобы определить, какая из решающих схем является оптимальной, необходимо прежде всего установить, в каком смысле понимается оптимальность. Выбор критерия оптимальности не является универсальным, он зависит от поставленной задачи и условий работы системы.
Пусть на вход приемника поступает сумма сигнала и помехи ![]() , где S
, где S![]() (t) — сигнал, которому соответствует кодовый символ ak,
(t) — сигнал, которому соответствует кодовый символ ak, ![]() — аддитивная помеха с известным законом распределения. Сигнал
— аддитивная помеха с известным законом распределения. Сигнал![]() . в месте приема является случайным с априорным распределением P(S
. в месте приема является случайным с априорным распределением P(S![]() ). На основании анализа колебания x(t) приемник воспроизводит сигнал
). На основании анализа колебания x(t) приемник воспроизводит сигнал ![]() . При наличии помех это воспроизведение не может быть совершенно точным. По принятой реализации сигнала приемник вычисляет апостериорное распределение,
. При наличии помех это воспроизведение не может быть совершенно точным. По принятой реализации сигнала приемник вычисляет апостериорное распределение,![]() содержащее все сведения, которые можно извлечь из принятой реализации сигнала x(t). Теперь необходимо установить критерий, по которому приемник будет выдавать на основе апостериорного распределения
содержащее все сведения, которые можно извлечь из принятой реализации сигнала x(t). Теперь необходимо установить критерий, по которому приемник будет выдавать на основе апостериорного распределения ![]() решение относительно переданного сигнала
решение относительно переданного сигнала ![]() .
.
При передаче дискретных сообщений широко используется критерий Котельникова (критерий идеального наблюдателя). Согласно этому критерию принимается решение, что передан сигнал ![]() , для которого апостериорная вероятность
, для которого апостериорная вероятность ![]() имеет наибольшее значение, т. е. регистрируется сигнал
имеет наибольшее значение, т. е. регистрируется сигнал ![]() если выполняются неравенства
если выполняются неравенства
![]() (5.2)
(5.2)
При использовании такого критерия полная вероятность ошибочного решения будет минимальной. Действительно, если по сигналу х принимается решение о том, что был передан сигнал ![]() ,-, то, очевидно, вероятность правильного решения будет равна
,-, то, очевидно, вероятность правильного решения будет равна ![]() , а вероятность ошибки
, а вероятность ошибки ![]() —Отсюда следует, что максимуму апостериорной вероятности
—Отсюда следует, что максимуму апостериорной вероятности ![]() соответствует минимум пол ной вероятности ошибки (5.1).
соответствует минимум пол ной вероятности ошибки (5.1).
На основании формулы Байеса (2.26)
![]() (5.3)
(5.3)
Тогда неравенство (5.2) можно записать в другом виде
![]() (5.4)
(5.4)
или
![]() (5.5)
(5.5)
Функцию p(x/s) часто называют функцией правдоподобия. Чем больше значение этой функции при данной реализации сигнала x, тем правдоподобнее, что передавался сигнал s. Отношение, входящее в неравенство (5.5)
![]() (5.6)
(5.6)
называется отношением правдоподобия. Пользуясь этим понятием, правило решения (5.5), соответствующее критерию Котельникова, можно записать в виде
![]() (5.7)
(5.7)
Если передаваемые сигналы равновероятны ![]() , то это правило решения принимает более простой вид
, то это правило решения принимает более простой вид
![]() (5.8)
(5.8)
Таким образом, критерий идеального наблюдателя сводится к сравнению отношений правдоподобия (5.7). Этот критерий является более общим и называется критерием максимального правдоподобия.
Рассмотрим бинарную систему, в которой передача сообщений осуществляется с помощью двух сигналов ![]() и
и ![]() , соответствующих двум кодовым символам а
, соответствующих двум кодовым символам а![]() и a
и a![]() . Решение принимается по результату обработки принятого колебания x(t) пороговым методом: регистрируется s
. Решение принимается по результату обработки принятого колебания x(t) пороговым методом: регистрируется s![]() если х<х0, и s2, если
если х<х0, и s2, если ![]() , где х0— некоторый пороговый уровень х. Здесь могут быть ошибки двух видов: воспроизводится s
, где х0— некоторый пороговый уровень х. Здесь могут быть ошибки двух видов: воспроизводится s![]() , когда передавался
, когда передавался ![]() и
и ![]() ,когда передавался s
,когда передавался s![]() . Условные вероятности этих ошибок (вероятности переходов) будут равны:
. Условные вероятности этих ошибок (вероятности переходов) будут равны:
![]() (5.9)
(5.9)
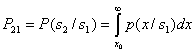 (5.10)
(5.10)
Значения этих интегралов могут быть вычислены как соответствующие площади, ограниченные графиком плотностей условного распределения вероятностей (рис. 5.2). Вероятности ошибок первого и второго вида соответственно:
![]() (5.11)
(5.11)
![]() (5.12)
(5.12)
Полная вероятность ошибки при этом
![]() (5.13)
(5.13)
Пусть p![]() =p
=p![]() , тогда
, тогда
![]()
Нетрудно убедиться, что в этом случае минимум Р0имеет место. При ![]() , т. е. при выборе порога в соответствии с рис. 5.2.
, т. е. при выборе порога в соответствии с рис. 5.2.
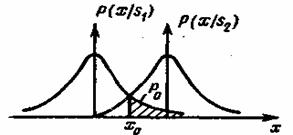
Рис. 5.2. График плотности условного распределения вероятностей при передаче сигналов st и s2
Для такого порога ![]() . На рис. 5.2 значение
. На рис. 5.2 значение ![]() определяется заштрихованной площадью. При любом другом значении порога величина
определяется заштрихованной площадью. При любом другом значении порога величина ![]() будет больше.
будет больше.
Несмотря на естественность и простоту, критерий Котельникова имеет недостатки. Первый заключается в том, что для построения решающей схемы, как это следует из соотношения (5.4), не-
обходимо знать априорные вероятности передачи различных символов кода. Вторым недостатком этого критерия является то, что все ошибки считаются одинаково нежелательными (имеют одинаковый вес). В некоторых случаях такое допущение не является правильным. Например, при передаче чисел ошибка в первых значащих цифрах более опасна, чем ошибка в последних цифрах. Пропуск команды или ложная тревога в различных системах оповещения могут иметь различные последствия.
Следовательно, в общем случае при выборе критерия оптимального приема необходимо учитывать те потери, которые несет получатель сообщения при различных видах ошибок. Эти потери можно выразить некоторыми весовыми коэффициентами, приписываемыми каждому из ошибочных решений. Обозначим потери ошибочных решений первого и второго видов соответственно ![]() и l
и l![]() . Тогда можно определить средние ожидаемые потери или средний риск
. Тогда можно определить средние ожидаемые потери или средний риск
![]() (5.14)
(5.14)
Оптимальной решающей .схемой будет такая, которая обеспечивает минимум среднего риска. Критерий минимального риска относится к классу так называемых байесовых критериев.
В радиолокации широко используется критерий Неймана — Пирсона. При выборе этого критерия учитывается, во-первых, что ложная тревога и пропуск цели не являются равноценными по своим последствиям, и, во-вторых, что неизвестна априорная вероятность передаваемого сигнала. Если пропуск цели является более нежелательным, то можно задать некоторую величину ![]() допустимой вероятности ложной тревоги и потребовать, чтобы решающая схема максимизировала вероятность правильного обнаружения Р
допустимой вероятности ложной тревоги и потребовать, чтобы решающая схема максимизировала вероятность правильного обнаружения Р![]() (или, что то же, минимизировать вероятность пропуска Р
(или, что то же, минимизировать вероятность пропуска Р![]() ).
).
Согласно критерию Неймана—Пирсона приемник является оптимальным в том случае, если при заданной вероятности ложной тревоги
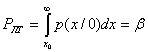 (5.15)
(5.15)
он обеспечивает наибольшую вероятность правильного обнаружения
![]() (5.16)
(5.16)
Можно показать, что критерий Неймана—Пирсона приводит к следующему правилу решения: цель считается обнаруженной, если
![]() (5.17)
(5.17)
где ![]() — некоторое число, определяемое допустимой вероятностью ложной тревоги
— некоторое число, определяемое допустимой вероятностью ложной тревоги ![]()

