9.4.1. Предел Шеннона

9.4.2. Энтропия

9.4.3. Неоднозначность и эффективная скорость передачи информации

Шеннон [3] показал, что пропускная способность канала C с аддитивным белым гауссовым шумом (additive white Gaussian noise — AWGN) является функцией средней мощности принятого сигнала S, средней мощности шума N и ширины полосы пропускания W. Выражение для пропускной способности (теорема Шеннона-Хартли) можно записать следующим образом.

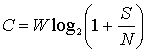(9.2)

Если W измеряется в герцах, а логарифм берется по основанию 2, то пропускная способность будет иметь размерность бит/с. Теоретически (при использовании достаточно сложной схемы кодирования) информацию по каналу можно передавать с любой скоростью со сколь угодно малой вероятностью возникновения ошибки. Если же , то кода, на основе которого можно добиться сколь угодно малой вероятности возникновения ошибки, не существует. В работе Шеннона показано, что величины S, N и W устанавливают пределы скорости передачи, а не вероятности появления ошибки. Шеннон [4] использовал уравнение (9.2) для графического представления доступных пределов производительности прикладных систем. Этот график, показанный на рис. 9.2, представляет нормированную пропускную способность канала C/W в бит/с/Гц как функцию отношения сигнал/шум (signal-to-noise ratio — SNR) в канале. График, представленный на рис. 9.3, изображает зависимость нормированной полосы пропускания канала W/C в бит/с/Гц от отношения сигнал/шум канала. Иногда рис. 9.3 используется как иллюстрация компромисса между мощностью и полосой пропускания, присущего идеальному каналу. Однако это не совсем компромисс [5], поскольку мощность обнаруженного шума пропорциональна полосе пропускания.

(9.3)

Подставив выражение (9.3) в уравнение (9.2) и немного преобразовав последнее, получаем следующее.

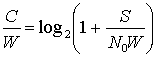(9.4)

Если битовая скорость передачи равна пропускной способности канала (R = С), то с помощью тождества (3.30) можно записать следующее.

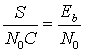(9.5)

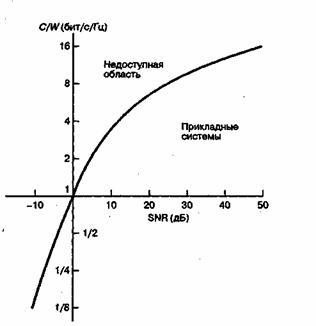
Рис. 9.2. Зависимость нормированной пропускной способности канала от SNR канала

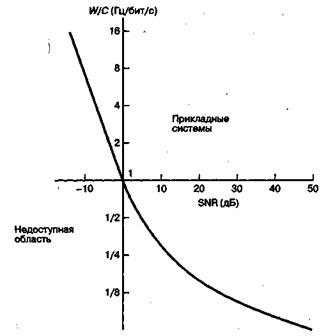
Рис. 9.3. Зависимость нормированной полосы пропускания канала от SNR канала

Таким образом, уравнение (9.4) можно модифицировать следующим образом.

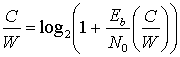(9.6, а)

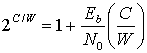(9.6 б)

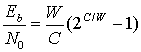(9.6 в)

На рис. 9.4 представлен график зависимости W/C от , описываемой формулой (9.6, в); асимптотическое поведение этой кривой при C/W (или W/C) рассматривается в следующем разделе.

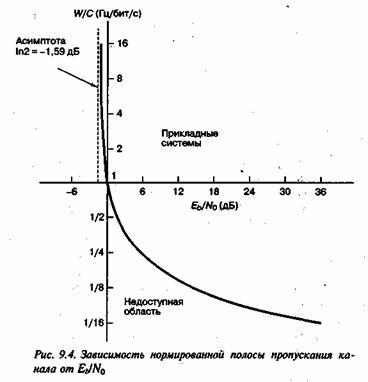
Рис. 9.4. Зависимость нормированной полосы пропускания канала от

9.4.1. Предел Шеннона

Существует нижнее предельное значение Et/N0, при котором, ни при какой скорости передачи нельзя осуществить безошибочную передачу информации. С помощью соотношения

можно рассчитать граничное значение .

Пусть

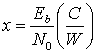
Тогда, из уравнения (9.6,а),

и

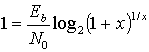
В пределе, при C/W, получаем

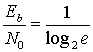= 0,693 (9.7)

или, в децибелах,

= -1,6дБ

Это значение называется пределом Шеннона (Shannon limit). На рис. 9.1, а предел Шеннона — это кривая зависимости РВот при k. При = -1,6 данная кривая скачкообразно изменяет свое значение с РВ= 1/2 на РВ =0. В действительности достичь предела Шеннона невозможно, поскольку k возрастает неограниченно, а с ростом k возрастают требования к полосе пропускания, и повышается сложность реализации системы. Работа Шеннона — это теоретическое доказательство существования кодов, которые могут улучшить или снизить требуемое значение от уровней некодированных двоичных схем модуляции до уровней, приближающихся к предельной кривой. При вероятности появления битовой ошибки 10^-5 двоичная фазовая манипуляция (binary phase-shift-keying — BPSK) требует значения , равного 9,6 дБ (оптимум некодированной двоичной модуляции). Следовательно, в данном случае в работе Шеннона указано, что теоретически, за счет использования кодирования, производительность можно повысить на 11,2 дБ по сравнению с некодированной двоичной модуляцией. В настоящее время большую часть такого улучшения (почти 10 дБ) можно получить с помощью турбокодов (см. раздел 8.4). Оптимальную разработку системы можно наилучшим образом представить как поиск рациональных компромиссов среди различных ограничений и взаимно противоречивых требований. Компромиссы модуляции и кодирования, т.е. выбор конкретных схем модуляции и кодирования для наилучшего использования переданной мощности и ширины полосы, являются очень важными, поскольку имеется много причин для снижения мощности, а также существует необходимость экономии спектра радиочастот.

9.4.2. Энтропия

Для разработки системы связи с определенной способностью к обработке сообщений нужна метрика измерения объема передаваемой информации. Шеннон [3] ввел такую метрику Н, называемую энтропией источника сообщений (имеющего л возможных выходных значений). Энтропия (entropy) определяется как среднее количество информации, приходящееся на один выход источника, и выражается следующим образом.

бит/выход источника (9.8)

Здесь pi — вероятность i-гo выходного значения и =1. Если сообщение двоичное или источник имеет только два возможных выходных значения с вероятностями р и , выражение для энтропии примет следующий вид.

(9.9)

Зависимость энтропии от р показана на рис. 9.5.

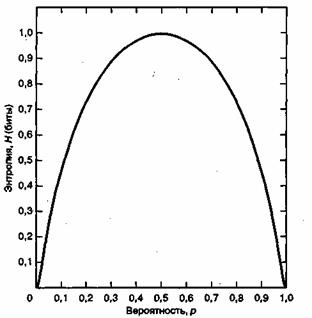
Рис. 9.5. Зависимость энтропии от вероятности (два события)

Величина Н имеет ряд особенностей.

1. Если логарифм в уравнении (9.8) берется по основанию 2, единица измерения Н — среднее число бит на событие. Здесь единица измерения бит — это мера количества информации, и ее не следует путать с термином "бит", означающим "двоичная цифра" (binary digit — bit).

2. Сам термин "энтропия" имеет несколько неопределенный смысл, что вызвано наличием нескольких формулировок в статистической механике. Для информационного источника с двумя равновероятными состояниями (например, выбрасывание монеты правильной формы) из рис. 9.5 видно, что неопределенность исхода и, следовательно, среднее количество информации максимальны. Как только вероятности уходят от равновероятного состояния, среднее количество информации снижается. В пределе, когда одна из вероятностей обращается в нуль, H также обращается в нуль. Результат известен до того, как произойдет событие, так что исход не несет в себе дополнительной информации.

3. Для иллюстрации связи между количеством информации и априорной вероятностью (если априорная вероятность сообщения на приемнике является нулем или единицей, сообщение можно не посылать) рассмотрим следующий пример. После девятимесячной беременности женщина оказывается в родильной палате. Муж с волнением ждет в приемной. Через некоторое время к нему подходит врач и говорит: "Примите мои поздравления, вы стали отцом". Какую информацию отец получил от врача после медицинского исхода! Почти никакой; отец практически достоверно знал, что ребенок должен родиться. Если бы врач сказал, "вы стали отцом мальчика" или "вы стали отцом девочки", он передал бы 1 бит информации, поскольку существует 50% вероятность того, что ребенок окажется девочкой или мальчиком.

Пример 9.2. Среднее количество информации в английском языке

а) Найдите среднее количество информации в бит/знак для английского языка, считая, что каждая из 26 букв алфавита появляется с равной вероятностью. Пробелы и знаки пунктуации не учитываются.

б) Поскольку буквы в английском языке (или каком-либо ином) появляются с различной частотой, ответ на п. а — это верхняя граница среднего количества информации на знак. Повторите п. а, считая, что буквы алфавита появляются со следующими вероятностями.

р = 0,10: для букв а, е, о, t

р = 0,07: для букв h, i, n, r, s

р =0,02: для букв с, d, f, I, m, p, u, у

р = 0,01: для букв b, g, j, k, q, v, w, x, z

Решение

а) 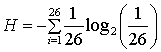=4,7 бит/знак

б) = = 4,17 бит/знак

Если 26 букв алфавита нужно выразить в некоторой двоичной схеме кодирования, то для каждой буквы требуется пять двоичных цифр. Пример 9.2 показывает, что должен существовать способ кодирования английского текста в среднем меньшим числом двоичных цифр для одной буквы (среднее количество информации, содержащееся в каждом знаке, меньше 5 бит). Подробнее тема кодирования источника будет рассмотрена в главе 13.

9.4.3. Неоднозначность и эффективная скорость передачи информации

Пусть по двоичному симметричному каналу (определенному в разделе 6.3.1) со скоростью 1000 двоичных символов/с происходит передача информации, а априорная вероятность передачи нуля или единицы одинакова. Допустим также, что помехи в канале настолько значительны, что, независимо от переданного символа, вероятность приема единицы равна 1/2 (то же самое — для нуля). В таком случае половина принятых символов должна случайно оказаться правильной, и может создаться впечатление, что система обеспечивает скорость 500 бит/с, хотя на самом деле никакой информации не передается. Одинаково "хороший" прием дает и использование "информации", поступившей из канала, и генерация этой "информации" методом подбрасывания правильной монеты. Утраченной является информация о корректности переданных символов. Для оценки неопределенности в принятом сигнале Шеннон [3] использует поправочный коэффициент, который называет неоднозначностью (equivocation).

Шеннон показал, что среднее эффективное количество информации Н^ в приемнике получается путем вычитания неоднозначности из энтропии источника.

Для системы, передающей равновероятные двоичные символы, энтропия Н(Х) равна 1 бит/символ. Если символы принимаются с Рв = 0,01, неоднозначность, как показано выше, равна 0,081 битДпринятый символ). Тогда, используя уравнение (9.11), можем записать эффективную энтропию Rед принятого сигнала.

Rед = 1 - 0,081 = 0,919 бит/полученный символ

Иными словами, если, например, за секунду передается R = 1000 двоичных символов, то Reff можно выразить следующим образом.

Reff = RHeS = 1000 символов/с х 0,919 бит/символ = 919 бит/с (9.12)

Отметим, что в предельном случае Рв= 0,5

Используя формулы (9.12) и (9.11) при R= 1000 символов/с, получаем

что и следовало ожидать.

Пример 9.3. Кажущееся противоречие с пределом Шеннона

График зависимости Pb от Eb|N0 обычно показывает плавный рост Рвпри увеличении Eb|N0. Например, кривые вероятности появления битовых ошибок на рис. 9.1 показывают, что в пределе при Eb|N0, стремящемся к нулю, Pb стремится к 0,5. Таким образом, кажется, что всегда (при сколь угодно малом значении Eb|N0) имеется ненулевая скорость передачи информации. На первый взгляд это не согласуется с величиной предела Шеннона Eb|N0= -1,6 дБ, ниже которого невозможна безошибочная передача информации или ниже которого даже бесконечная полоса пропускания дает конечную скорость передачи информации (см. рис. 9.4).

а) Предложите способ разрешения кажущегося противоречия.

б) Покажите, каким образом коррекция неоднозначности по Шеннону может помочь разрешить данное противоречие для двоичной системы с модуляцией PSK, если энтропия источника равна 1 бит/символ. Предположим, что рабочая точка на рис. 9.1, б соответствует Eb|N0= 0,1 (-10 дБ).

Решение

а) Величина Eb, традиционно используемая при расчетах каналов в прикладных системах, — это энергия принятого сигнала, приходящаяся на переданный символ. Однако Eb, в уравнении (9.6) — это энергия сигнала, приходящаяся на один бит принятой информации. Для разрешения описанного выше кажущегося противоречия следует учитывать потери информации, вызываемые помехами канала.

б) На основе уравнения (4.79) для BPSK можно записать

.

где Q определено в формуле (3.43) и представлено в табличной форме в приложении Б (табл. Б.1). Из таблицы находим, что РВ = 0,33. Далее находим неоднозначность и эффективную энтропию.

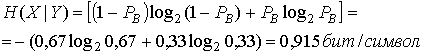
Следовательно,

Таким образом, эффективное значение Eb|N0 равно 0,7 дБ на принятый информационный бит, что значительно больше предела Шеннона -1,6 дБ.