Рассмотрим один из элементов дискретной цепи - элемент задержки (рис. 34). Сигнал на его входе , а на выходе . Напомним, что z-изображения дискретных сигналов и имеют вид:

, .

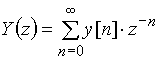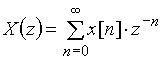Тогда, воспользовавшись теоремой задержки, можно записать z-преобразование для равенства :

.

Отношение z-изображений выходного и входного дискретных сигналов называют передаточной (или системной) функцией дискретной цепи :

.

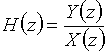Тогда .

В таком случае передаточная функция элемента задержки:

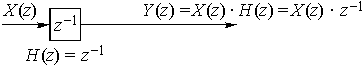
Рис. 36

(рис. 36).

Обратимся теперь к выражению (17). На основании теоремы свертки z-преобразование дискретной свертки равно произведению z-преобразований дискретных сигналов:

.

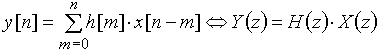Из последнего выражения видно, что z-преобразование дискретной импульсной реакции есть передаточная функция дискретной цепи:

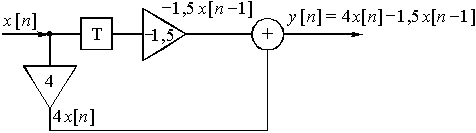
Рис. 37

.

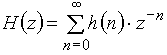Пример 14.1. Найдем импульсную характеристику и передаточную функцию дискретной цепи (рис. 37), выходная последовательность которой задана выражением .

Отсчеты дискретной импульсной характеристики - это отсчеты , рассчитанные при условии, что на вход цепи подается дискретная d-функция, т.е. = {1; 0; 0; ...}.

,

,

при n> 1.

Таким образом, отсчеты дискретной импульсной характеристики = {4; -1,5} соответствуют коэффициентам усиления усилителей в схеме (рис. 37).

Для нахождения передаточной функции возьмем z-преобразование дискретной импульсной характеристики

.

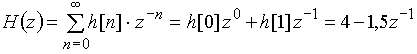Другой способ нахождения передаточной функции заключается в том, чтобы определить z-изображение выходной последовательности, а затем найти как отношение и :

или

.

Очевидно, что . Z-изображение дискретной цепи с такой передаточной функцией приведено на рис. 38.

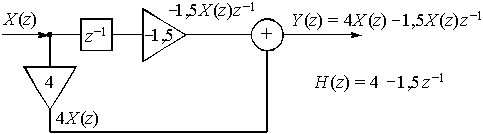
Рис. 38

Пример 14.2. Найдем отсчеты выходного сигнала дискретной цепи, z-изображение которой приведено на рис. 39, а входной сигнал = {-2; 1; 2; -1}.

Найдем z-изображение входного сигнала :

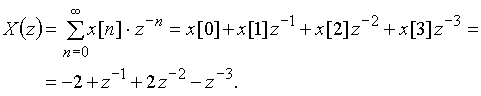
Передаточная функция цепи (рис. 39) . Она находится непосредственно по схеме либо как z-изображение дискретной импульсной характеристики = {-1; 1; 2}.

Найдем z-изображение выходного сигнала

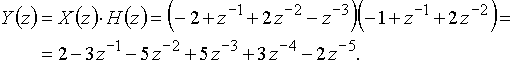
Коэффициенты при z в отрицательных степенях в этом выражении являются отсчетами выходного сигнала (рис. 29):

= {2; -3; -5; 5; 3; -2}.

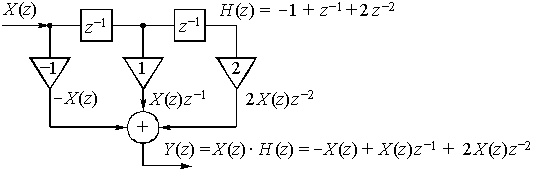
Рис. 39

Пример 14.3. Найдем передаточную функцию дискретной цепи, входная и выходная последовательности которой имеют вид

= {1; 0; 1; 2}, = {0; 1; 2; 1}.

Z-изображения последовательностей

;

.

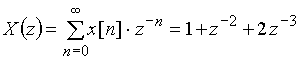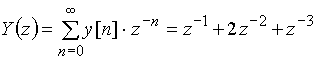Следовательно, передаточная функция

.

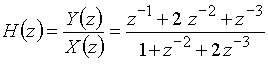Разделив числитель передаточной функции на знаменатель, можно представить в виде

.

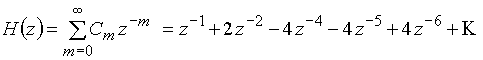Самоконтроль

1. Что такое передаточная функция дискретной цепи?

2. Чему равна передаточная функция элемента задержки?

3. Как связаны передаточная функция и импульсная характеристика дискретной цепи?

4. Найдите передаточную функцию дискретной цепи, если = = {1; 1; 1}, = {0; 0; 1}.

5. Найдите передаточную функцию цепи, дискретная импульсная характеристика которой имеет вид = {1; -2; 3}.

6. Приведите структурную схему цепи, имеющей передаточную функцию .