В соответствии с методологией теории систем для описания процессов функционирования сетей связи (в том числе и МССС) используем функциональное уравнение:
![]() , (2.1)
, (2.1)
где ![]() параметры, а G – её структура [30, 32, 35, 36]. При этом под параметром понимается величина, характеризующая свойства сети связи. Различают внутренние (параметры отдельных элементов), внешние (параметры внешней среды, оказывающие влияние на функционирование сети) и выходные (определяющие степень выполнения целевого предназначения) параметры.
параметры, а G – её структура [30, 32, 35, 36]. При этом под параметром понимается величина, характеризующая свойства сети связи. Различают внутренние (параметры отдельных элементов), внешние (параметры внешней среды, оказывающие влияние на функционирование сети) и выходные (определяющие степень выполнения целевого предназначения) параметры.
В свою очередь структура сети (её морфологическая модель) задается неориентированным графом ![]() , где [32, 36–39, 94]:
, где [32, 36–39, 94]:
![]() – множество вершин (узлов связи – УС), декомпозируемых на совокупность узлов доступа и узлов магистральной сети и характеризуемых координатами их размещения, относительно которых определяются элементы матрицы расстояний между узлами связи
– множество вершин (узлов связи – УС), декомпозируемых на совокупность узлов доступа и узлов магистральной сети и характеризуемых координатами их размещения, относительно которых определяются элементы матрицы расстояний между узлами связи ![]() ;
;
![]() – множество ребер (сетка линий связи – ЛС), характеризуемых родом связи и вектором пропускных способностей
– множество ребер (сетка линий связи – ЛС), характеризуемых родом связи и вектором пропускных способностей ![]() ;
;
![]() – множество элементов графа, где
– множество элементов графа, где ![]() ,
, ![]() ,
, ![]() – число элементов (мощность) множеств N, M, D.
– число элементов (мощность) множеств N, M, D.
Каждому элементу графа ставится в соответствие количественный параметр ![]() , который обычно называют обобщённой стоимостью. При этом матрица стоимостей задается массивом
, который обычно называют обобщённой стоимостью. При этом матрица стоимостей задается массивом ![]() [32, 36–39]. Каждый элемент графа
[32, 36–39]. Каждый элемент графа ![]() статистически независимо отказывает с известными вероятностями отказа [28, 37].
статистически независимо отказывает с известными вероятностями отказа [28, 37].
Матрицы смежности ![]() и инциденций
и инциденций ![]() неориентированного графа
неориентированного графа ![]() задаются в следующем виде:
задаются в следующем виде:
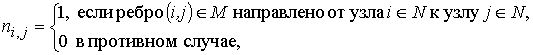 (2.2)
(2.2)
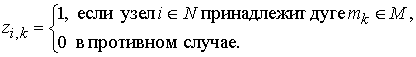 (2.3)
(2.3)
Матрица информационных тяготений ![]() ,
, ![]() определяет интенсивность передаваемого потока r-го класса между i-м и j-м узлами графа
определяет интенсивность передаваемого потока r-го класса между i-м и j-м узлами графа ![]() .
.

