12.1. Частотно-сдвинутые бинарные m-последовательности

12.2. Ансамбли последовательностей Голда

12.3. Множества Касами и их расширения

12.4. Ансамбли Камалетдинова

Известен единственный нетривиальный пример ансамбля сигнатур, корреляционный пик которого строго удовлетворяет границе Велча – ансамбль кубичных вычетов. Однако данный ансамбль представляет скорее теоретический, чем практический интерес, поскольку свидетельствует только об обоснованности представленной границы.

С другой стороны, список известных асимптотически оптимальных ансамблей достаточно представителен. Среди других он включает множество кодов, которое, в отличие многофазных кодов с идеальной ПАКФ, может иметь и практическую значимость. Одной из причин этому служит тот факт, что объем алфавита этих ансамблей фиксирован и не возрастает с увеличением длины N. Так например, существуют ансамбли с трехфазным алфавитом длины , состоящие из сигнатур и обладающие величиной корреляционного пика, стремящегося к границе Велча при

Ниже ограничимся лишь кратким обсуждением тех из них, которые либо нашли широкое практическое применение, либо особо показательны на фоне остальных.

12.1. Частотно-сдвинутые бинарные m-последовательности

Возьмем бинарную m-последовательность периода и используем ее в качестве сигнатуры для первого пользователя. Сформируем остальные сигнатур посимвольным умножением на дискретные гармоники частот :

.

Тогда квадрат модуля периодической ВКФ k-й и l-й последовательностей

.

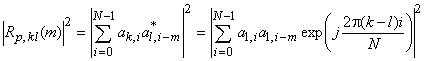Рассмотрим вначале случай , т.е. . Тогда, если , то получаем основной лепесток АКФ k-й сигнатуры, т.е. . Если же , то сумма в выражении для ВКФ есть сумма всех корней из единицы степени N и, значит, равна нулю.

Пусть теперь . Тогда, согласно свойству сдвига и сложения m-последовательностей, для некоторого t, и квадрат модуля ВКФ

,

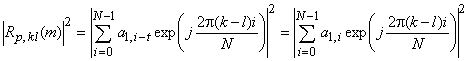что оказывается -й компонентой энергетического ДПФ-спектра последовательности . Поскольку энергетический спектр последовательности есть ДПФ от ее периодической АКФ, а последняя равна –1 для любого ненулевого сдвига и при , то

.

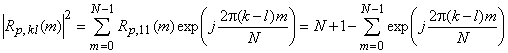Последняя сумма отличается от нуля и равна N только при , так что, сводя вместе все полученные результаты и переходя к нормированным корреляциям, имеем

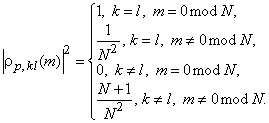
Отсюда видно, что корреляционный пик ансамбля

,

т.е. практически совпадает с границей Велча. Таким образом, рассматриваемый ансамбль является асимптотически оптимальным и эффективным образом реализует асинхронную схему CDMA.

Одним из его достоинств в сравнении с другими многофазными ансамблями является возможность генерирования сигнатур простым сдвигом несущей частоты. Действительно, сдвиг несущей на эквивалентен линейному приращению фазы между последовательными чипами на , что в точности совпадает с предписанием правила формирования ансамбля.

Очевидно, что осуществление сдвига частоты не составляет значительной проблемы для современной электроники. Блестящим подтверждением этому служит использование указанного ансамбля в российской глобальной навигационной системе космического базирования ГЛОНАСС, в которой для организации дальномерного канала пониженной точности применяются кодовые сигнатуры данного вида длины с длительностью чипа 2 мксек.

Хотя известно достаточно много и других многофазных минимаксных ансамблей, бинарные семейства традиционно считаются приоритетными в плане технологической привлекательности, поэтому остальная часть раздела посвящается некоторым важным примерам ансамблей бинарных сигнатур.

12.2. Ансамбли последовательностей Голда

Метод построения последовательностей Голда основывается на использовании бинарных последовательностей максимальной длины. Пусть имеется бинарная –последовательность длины . Путем децимации с индексом вида

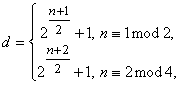
построим последовательность с таким же периодом . Децимация означает выбор каждого -го символа последовательности и запись выбранных символов друг за другом, так что . Сформируем ансамбль из K сигнатур следующим образом

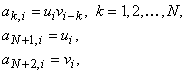
где . Выражая это словесно, строим сигнатур посимвольным перемножением на циклические копии , а в качестве еще двух сигнатур берем сами исходные -последовательности. В итоге имеем всего сигнатур. На практике традиционно бинарные -последовательности формируются сначала в алфавите , т.е. над полем с помощью РСЛОС, с последующим отображением элементов на вещественную пару . Поэтому удобна реализация правила конструирования ансамбля с помощью двух -разрядных РСЛОС, генерирующих предшественники и последовательностей и . Тогда, взамен умножения на , можно просуммировать предшественники по модулю 2 с последующим отображением результата на множество : . Следующий рисунок иллюстрирует практическое воплощение конструкции Голда в описанном варианте.

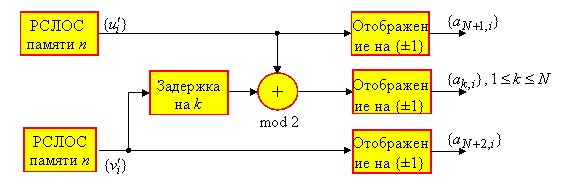
Оценка корреляционного пика ансамбля Голда приводит к следующему результату

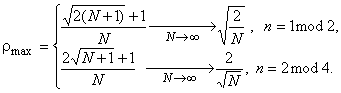
Как видно, при любом нечетном значении памяти n ансамбли сигнатур Голда асимптотически близки к нижней границе Сидельникова, т.е. оптимальны, тогда как при четном n, не кратном четырем, их проигрыш в уровне по отношению к граничному составляет около 3 дБ. Следует отметить, что при ансамбль Голда также существует с тем же значением корреляционного пика, как и при , но с числом последовательностей на одну меньше.

Ансамбли Голда пользуются исключительной популярностью в современных CDMA системах. Достаточно сказать, что они используются в глобальной спутниковой навигационной системе GPS для разделения сигналов космических аппаратов, в 3G системе мобильной связи стандарта WCDMA для скремблирования CDMA кодов и т.п.

Пример 12.2.1. Построим последовательности Голда длины . Ансамбль столь малой длины практически бесполезен, однако помогает в иллюстрации идеи конструкции. Начнем с бинарной m-последовательности, впервые встретившейся в примере 8.3.1: . Индекс децимации удовлетворяет оговоренным условиям. В результате децимации имеем последовательность . Посимвольное суммирование и по модулю два дает последовательность , которая после отображения на алфавит превращается в первую последовательность Голда . Сдвиг вправо на одну позицию и сложение по модулю 2 с дает последовательность , которая после перехода к символам становится второй последовательностью Голда . Еще пять последовательностей Голда получаются в результате дальнейших сдвигов , сложения по модулю 2 с и изменения символов на . Совместно с и , преобразованными к алфавиту , имеем последовательностей всего. Проверка оптимальности корреляционного пика в этом простейшем случае не имеет особого смысла, поскольку заранее ясно, что при ненормированная периодическая корреляция (кроме основного лепестка АКФ) не может превзойти значения 5.

12.3. Множества Касами и их расширения

Конструкция Касами в принципиальном плане весьма близка к описанной выше конструкции Голда. Выполним децимацию бинарной m-последовательности четной памяти с индексом . Очевидно, это значение d не взаимно просто с периодом последовательности , так что полученная последовательность имеет период, являющийся делителем N. Можно показать, что если инициализирована так, что , то «короткая» последовательность окажется бинарной m-последовательностью периода .

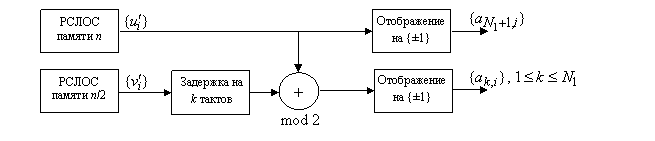
В данной схеме сигнатур Касами длины N образуются посимвольным перемножением исходной «длинной» m-последовательности с различными циклическими копиями , а еще одной сигнатурой служит сама длинная последовательность, так что:

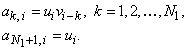
где . Таким образом, имеется всего таких сигнатур периода N. Разумеется, вновь умножение последовательностей , можно выполнить как сложение по модулю 2 их предшественников , , но в отличие от ансамбля Голда для формирования короткой последовательности требуется РСЛОС вдвое меньшей длины (см. рисунок на следующем слайде).

Ансамбль Касами также обладает минимаксными свойствами

.

Сравнение двух бинарных ансамблей показывает значительный (6 дБ) выигрыш множеств Касами в уровне корреляционного пика у ансамблей Голда той же длины в обмен на значительно меньшее (в раз) числа сигнатур K.

Следует отметить, что для бинарных сигнатур границы корреляционного пика можно несколько уточнить, учтя, что их ненормированные корреляции принимают только целочисленные значения. В результате выясняется, что как ансамбли Голда с нечетной памятью, так и ансамбли Касами строго (а не только асимптотически) оптимальны по уровню корреляционного пика среди всех бинарных сигнатурных ансамблей.

Пример 12.3.1. Построим ансамбль Касами длины . Начнем с бинарной m-последовательности длины на основе примитивного полинома с начальным состоянием РСЛОС . Имеем . Децимация этой последовательности с индексом дает m-последовательность периода три . Сумма по модулю 2 последовательности с тремя сдвинутыми копиями после перехода к алфавиту образует первые три сигнатуры Касами:

,

,

.

Четвертой служит после преобразования символов в : . Непосредственная проверка показывает, что все их ненормированные ВКФ, как и боковые лепестки ненормированных АКФ первых трех последовательностей, принимают лишь значения –5 и 3, так что .

Сравнительно малое число сигнатур в обсуждаемом множестве придает особую важность найденному Б. Ж. Камалетдиновым элегантному методу почти двукратного расширения ансамбля Касами без ухудшения корреляционного пика. Пусть n кратно 4: , где r – целое, так что . При такой длине в дополнение к множеству Касами существует и другой бинарный ансамбль того же объема , называемый ансамблем бент-последовательностей и обладающий тем же минимаксным свойством . В самых общих чертах построение бент-последовательностей вновь состоит в посимвольном перемножении двух исходных последовательностей: «длинной» m-последовательности периода и некоторой специальной последовательности, базирующейся на так называемой бент-функции. Детали такой конструкции достаточно замысловаты и здесь не обсуждаются, однако принципиальным является то, что нормированная ВКФ любой бент-последовательности с любой из первых последовательностей Касами по абсолютной величине не превосходит корреляционного пика ансамблей Касами и бент-последовательностей. В итоге можно составить ансамбль, включающий последовательностей Касами и бент-последовательностей и обладающий прежним значением корреляционного пика . Полученный таким образом ансамбль уникален в том смысле, что среди всех известных бинарных ансамблей с корреляционным пиком только он содержит наибольшее число сигнатур .

12.4. Ансамбли Камалетдинова

Известны и другие бинарные минимаксные ансамбли, нередко отличающиеся от рассмотренных лишь тонкой структурой последовательностей, но не значениями длины N, объема K и корреляционного максимума . На этом фоне заслуживают особого интереса ансамбли, открытые Б. Ж. Камалетдиновым и существующие для длин, отличных от длин ансамблей Голда и Касами.

Чтобы нагляднее описать идею, остановимся на несколько суженной версии конструкций Камалетдинова, что, однако, не сопряжено с какими-либо изъятиями в части охватываемых длин или достижимых параметров. В первой схеме Камалетдинова возьмем простое нечетное вида и расширим определение двузначного характера из раздела 8.4 на нулевой элемент , положив ( приведет к тому же конечному результату). Отождествим номер символа в последовательности с элементом поля , оперируя с ним по модулю p, и образуем p-ичных последовательностей над (т.е. с элементами из этого поля) по правилу:

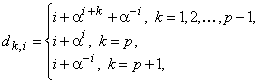
где вся арифметика соответствует правилам, – примитивный элемент и . Можно заметить, что каждая последовательность образована суммированием последовательностей с взаимно простыми периодами p и p–1 и, следовательно, ее период . Отобразим теперь данные последовательности на бинарный алфавит , используя введенное расширение двузначного характера

.

Полученный таким образом ансамбль бинарных сигнатур имеет параметры

.

Длину N можно сделать достаточно большой выбором , имея и , что после сравнения с границей свидетельствует об оптимальности (по меньшей мере, асимптотической) ансамбля по уровню корреляционного пика.

Пример 12.4.1. Пусть . Прямая проверка подтверждает, что элемент примитивен в . Тогда последовательности и вида и соответственно обе имеют период . Комбинирование их по модулю 7 с последовательностью периода 7, предписываемое (7.57), дает семеричных последовательностей периода . Первая из них, например, . Замена семеричных элементов их расширенными характерами согласно правилу и преобразует последовательности в 8 бинарных сигнатур, например, .

Вторая схема Камалетдинова использует как основу p-ичную линейную последовательность , полученную децимацией с индексом сдвигов p-ичной m-последовательности памяти , т.е. длины . Поскольку d делит , то последовательность имеет период . Теперь построим последовательностей над

и отобразим их на бинарный алфавит , используя введенное расширение двузначного характера. В результате получим ансамбль бинарных сигнатур с параметрами

.

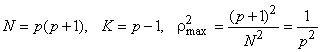Вновь при больших длинах отношение и , подтверждая оптимальность (по меньшей мере, асимптотическую) и этого ансамбля.

Пример 12.4.1. В данном случае отсутствует запрет на и -ичная m-последовательность памяти и длины может быть сформирована с помощью примитивного полинома над второй степени , или, эквивалентно, с помощью рекурсии . При начальном состоянии РСЛОС последовательность . Децимация ее сдвигов с индексом , дает две последовательности периода 4: и . После посимвольного сложения с последовательностью получатся последовательностей периода : и . Последний шаг, состоящий в замене их элементов расширенными характерами , , приведет к ансамблю Камалетдинова из двух бинарных последовательностей длины : и . Найти их АКФ и ВКФ можно вручную, убедившись в итоге в справедливости равенства .

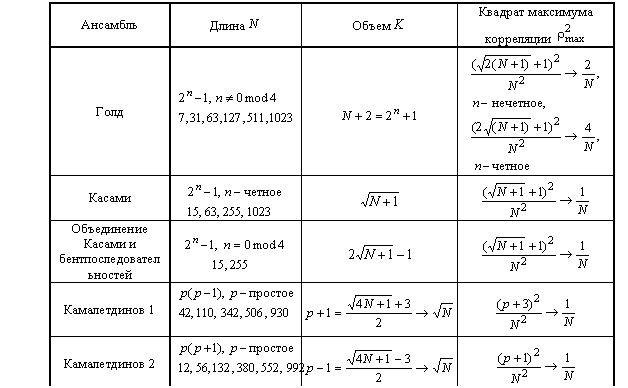
Резюмируем итоги предпринятого анализа в форме таблицы, представляющей длину (с перечислением всех длин существующих ансамблей в диапазоне ), число сигнатур и квадрат максимума корреляции бинарных сигнатурных ансамблей. Таблица весьма выразительно демонстрирует весомость конструкций Камалетдинова: в оговоренном интервале они добавляют 11 новых длин к тем восьми, для которых существуют ансамбли Голда и Касами.