1. Общие сведения по электронным и квантовым приборам СВЧ и оптического диапазонов
1.1. Особенности работы СВЧ приборов
1.2. Основные параметры, используемые для оценки ЭП СВЧ диодов
3.1. Пролетный двухрезонаторный клистрон
3.2. Двухрезонаторные клистронные генераторы
3.3. Многорезонаторные клистроны
4. Лампы бегущей волны типа О (ЛБВО)
4.1. Принцип работы лампы бегущей волны
4.3. Элементы линейной теории ЛБВ
4.4. Параметры и характеристики ЛБВ
5. Полупроводниковые диоды и транзисторы СВЧ
5.4. Переключательные диоды СВЧ
6. Лавинно-пролетные диоды (ЛПД)
6.1. Лавинное умножение носителей заряда
6.2. Пролетный режим работы ЛПД
6.3. Параметры и характеристики генераторов и усилителей на ЛПД в пролетном режиме
7. Эффект Ганна и приборы на его основе
7.4. Режимы работы диодов Ганна
7.5. Конструктивное оформление и основные параметры диодов Ганна
8. Физические основы квантовых приборов
8.3. Ширина спектральной линии
8.4. Возможность усиления и генерации в квантовых системах
8.5. Взаимодействие бегущих электромагнитных волн с активной средой
9.1. Создание инверсной населенности в полупроводниках
9.2. Лазеры на гетеропереходах
9.3. Открытый оптический резонатор
9.4. Характеристики излучения в оптическом диапазоне
9.6. Гелий-неоновый атомный лазер
9.11. Жидкостные и химические лазеры
1. Общие сведения по электронным и квантовым приборам СВЧ и ОД
Диапазон сверхвысоких частот (СВЧ) занимает полосу частот от 300 МГц до 300 ГГц, что соответствует длинам волн 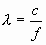 от 1 м до 1 мм. Диапазон СВЧ включает в себя:
от 1 м до 1 мм. Диапазон СВЧ включает в себя:
- дециметровые волны (ДМВ) 300 МГц < f < 3 ГГц, 1 м > l > 10 см;
- сантиметровые волны (СМВ) 3 ГГц < f < 30 ГГц, 10 см > l > 1 см;
- миллиметровые волны (ММВ) 30 ГГц < f < 300 ГГц, 1 см > l .
Оптический диапазон -10 “ Гц < f < 1015 Гц включает в себя:
- субмиллиметровые волны 1мм > l > 0,1 мм;
- инфракрасные волны 0,1 мм > l > 0,8 мкм;
- видимые волны 0,8 мкм > l > 0,4 мкм;
- ультрафиолетовые волны 0,4 мкм > l.
Диапазоны СВЧ и оптический обладает многими отличительными особенностями. Некоторые из них, наиболее важные для нас, связистов, мы сейчас отметим.
- Большая информационная емкость. Если в диапазонах длинных, средних и коротких волн, вместе взятых можно организовать только три тысячи радиотелефонных каналов с полосой 10 кГц, то в диапазоне СВЧ можно организовать около 30 миллионов таких каналов, т.е. почти в 10 тысяч раз больше. Еще больше каналов можно бы было организовать в оптическом диапазоне.
- С помощью не очень сложных устройств электромагнитные колебания СВЧ диапазонов могут фокусировать и излучаться направленно узкими пучками. Вследствие этого заданную напряженность поля в нужной нам точке пространства можно обеспечить при значительно меньшей мощности передатчика, чем, скажем, в КВ диапазоне. Другое немаловажное обстоятельство: благодаря высокой пространственной избирательности, т.е. высокой направленности передающих и приемных антенн, на СВЧ очень малы взаимные помехи между различными системами связи. Если учесть, что уровень естественных помех на СВЧ очень мал, то основным видом являются собственные шумы приемника. Иную картину мы наблюдаем на КВ диапазоне, где также мал уровень естественных шумов, а значительный шумовой фон создают “отголоски” работающих передающих станций.
- Колебания СВЧ и оптического диапазонов легко проникают сквозь ионизированные слои атмосферы Земли. Это обстоятельство делает особенно привлекательным использование СВЧ для связи с космическими объектами.
- Электромагнитные колебания СВЧ могут распространяться не только в свободном пространстве, но и в специальных линиях передачи – волноводах. Следовательно, имеется возможность построения очень широкополосных волноводных систем связи.
- Квант энергии СВЧ колебаний hn сравним с разностью энергетических уровней молекул и атомов вещества (Н = 6,6·10-34 Дж·с – постоянная Планка). Эта особенность используется в радиоспектроскопии, т.е. при изучении внутреннего строения вещества по спектрам испускания и поглощения.
Рассмотрение этих особенностей показывает важность и необходимость освоения диапазонов СВЧ и оптического для целей многих областей науки и техники и, в частности, для целей связи. Для освоения какого-либо диапазона необходимо уметь:
- генерировать монохроматические колебания достаточной мощности;
- улавливать и усиливать радиоволны очень малой мощности, несущие полезную информацию;
- преобразовывать электромагнитные колебания одной частоты в колебания другой частоты;
- модулировать генерируемые колебания данного диапазона волн колебаниями, несущими полезную информацию;
- демодулировать принятые и усиленные радиоволны с целью выделения из них модулирующих колебаний, несущих полезную информацию.
В диапазоне СВЧ эти функции выполняют электронные и квантовые приборы СВЧ, изучение которых и является задачей данного курса. Электронными приборами СВЧ называются приборы для генерации усиления или преобразования электромагнитных колебаний СВЧ диапазона посредством взаимодействия электромагнитного поля с потоками электронов, движущимися в вакууме или твердом теле. В основе электронных приборов СВЧ лежит тот же принцип взаимодействия движущихся электронов с электромагнитным полем, что и у электронных приборов низких частот. Но устройства этих приборов существенно различны (показать) параметры обычных электронных радиоламп с повышением частоты становятся все более неудовлетворительными из-за роста потерь мощность в проводниках и диэлектриках, из-за воздействия паразитных емкостей и индуктивностей, а также из-за возрастающего влияния электронов. Этим объясняется вынесение изучения электронных приборов СВЧ совместно с квантовыми приборами и в отдельный курс. Квантовыми приборами называются приборы для генерации усиления или преобразования электромагнитных колебаний СВЧ и оптического диапазона посредством взаимодействия электромагнитного поля с атомами, молекулами или ионами вещества. В квантовых приборах происходит передача СВЧ полю внутренней энергии атомов, молекул или ионов.
Электронные и квантовые приборы СВЧ несмотря на свою молодость – история развития насчитывает соответственно около 50 и 35 лет – нашли широкое применений в радиолокационной технике и технике связи. Эти приборы работают в телевизионных передатчиках, в передатчиках и приемниках радиорелейных линий связи, в спутниковых системах связи и телевидения. Уже сейчас сеть приемных станций “Орбита” довольно широка, широкое распространение получили спутниковые системы связи, позволяющие избирательно устанавливать двусторонние связи между любыми пунктами нашей планеты. Многим из вас как будущим инженерам радиосвязи и радиовещания придется разрабатывать, строить и обслуживать технику СВЧ. Отсюда вытекает важность изучения курса “Электронные и квантовые приборы СВЧ” в стенах нашего института.
1.1. Особенности работы СВЧ приборов
Период колебаний ![]() в СВЧ диапазон мал, и имеет порядок 10-9 сек. Время движения носителей зарядов между рабочими электродами приборов t, и имеет такой же порядок 10-9 сек.
в СВЧ диапазон мал, и имеет порядок 10-9 сек. Время движения носителей зарядов между рабочими электродами приборов t, и имеет такой же порядок 10-9 сек.
Таким образом, время пролета сравнимо с периодом колебаний – электронный прибор становится инерционным (причем, если t³T, то прибор становится неуправляемый).
Таким образом, время пролета необходимо делать меньше, но есть предел: уменьшение расстояния между электродами увеличивает емкость: во избежании увеличения С необходимо уменьшать площадь электронов, но это приведет к уменьшению тока и выходной мощности. Необходимо разрабатывать приборы в которых время пролета не играло вредной роли.
Любой ЭП имеет межэлектродные емкости, а любой проводник обладает индуктивностью (1 см = 10-7 Гн). Поэтому с ростом f растут паразитные реактивные составляющие, которые приводят:
- к уменьшению входного сопротивления;
- образованию паразитных каналов (путей) прохождения сигналов по прибору, нарушающих его нормальную работу.
Размеры электродов l становятся соизмеримы с длиной волны l . А если ![]() , то получается антенна и ЭП начинает активно излучать. С ростом f растут потери в металле и диэлектрике. Для их уменьшения используют:
, то получается антенна и ЭП начинает активно излучать. С ростом f растут потери в металле и диэлектрике. Для их уменьшения используют:
- специальные виды керамики с малыми диэлектрическими потерями;
- серебрение и золочение электродов.
В СВЧ диапазоне в качестве резонансных колебательных систем используют отрезки линий или полые резонаторы, которые нужно соединять с ЭП. При соединении возникают проблемы, как сделать прибор, чтобы он легко соединялся с колебательной системой? Многие приборы изготавливают с внутренней колебательной системой.
1.2. Основные параметры, используемые для оценки ЭП СВЧ диапазона
- Генераторные приборы.
РВЫХ
Диапазон перестройки
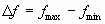 ,
, 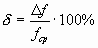 .
.Нестабильность частоты:
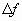 - уход частоты в результате воздействия каких-либо дестабилизирующих факторов.
- уход частоты в результате воздействия каких-либо дестабилизирующих факторов.По стабильности генераторы делятся на:
- стабильные
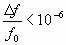 ;
;- нестабильные
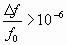 .
. - Усилительные приборы.
Коэффициент усиления по мощности
Рабочая полоса частот (без перестройки).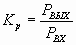 (в разах),
(в разах), 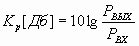 .
.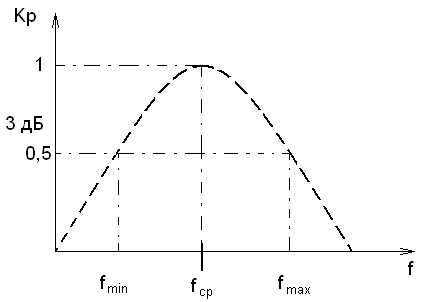
Рис. 1.1
Обычно полоса частот определяется по половинной мощности (3 дБ)
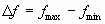 . Часто полоса приводится относительно
. Часто полоса приводится относительно 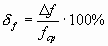 . В связи с этим, приборы делят на узкополосные (
. В связи с этим, приборы делят на узкополосные (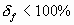 ) и широкополосные (
) и широкополосные (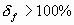 ). Коэффициент шума (
). Коэффициент шума (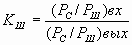 ).
).Параметр играет важную роль при слабом сигнале, т.е. во входных каскадах приемников.
- Общие параметры.
IРАБ, UРАБ, Рпотребляемая, КПД, h .
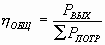 .
.
Контрольные вопросы.
1. Определение СВЧ и оптического диапазона. Какие поддиапазоны волн (частот) входят в эти диапазоны. 2. Какие функции выполняют СВЧ электронные приборы. 3. Особенности диапазона СВЧ и ОД. 4. Основные параметры электронных приборов СВЧ.
2. Триоды и тетроды СВЧ
Полный ток в промежутке между электродами и во внешней цепи электровакуумных приборов. Как известно, в электронных лампах используется электростатическое управление электронным потоком, заключающееся в том, что изменение напряженности электрического поля в рабочем объеме лампы вызывает изменение высоты потенциального барьера для электронов в области объемного заряда около катода, а следовательно, изменение числа электронов, участвующих в создании тока.
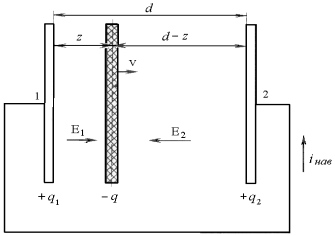
Рис. 2.1
При переменных напряжениях на электродах лампы ток можно считать безынерционной функцией напряжения, если время пролета электронов в промежутке между электродами т много меньше периода переменного напряжения Т. Такой режим работы получил название квазистатического режима.
Однако с ростом частоты время пролета может оказаться сравнимым с периодом переменного напряжения и больше его. В этом случае необходимо учитывать, что за время пролета электрона сильно изменяются напряжение на электродах и электрическое поле в пространстве между ними. Если амплитуда переменного напряжения велика, возможно, даже возвращение электронов к катоду. Теперь связь мгновенных значений токов и напряжений не соответствует связи в статическом или квазистатическом режиме.
Для учета влияния времени пролета электронов на токи электродов применяется понятие наведенного тока, которое будет использовано и при рассмотрении специальных приборов СВЧ.
Рассмотрим два плоских электрода (рис. 2.1) с равными потенциалами. Предположим, что от электрода 1 к электроду 2 движется тонкий электронный слой с общим зарядом — q.
Вследствие явления электростатической индукции отрицательный заряд - q наводит на электродах положительные поверхностные заряды q 1 и q 2 , так что
q1+ q2 = q. (2.1)
Введем обозначения: ε 0 – диэлектрическая постоянная вакуума;
S – площадь электродов; d– расстояние между электродами.
Используя теорему Гаусса, можно определить напряженности поля у поверхности электродов:
E1= q1 / ε0 S ; E2=q2 / ε0 S. (2.2)
Очевидно, что
E1 z - E2( d - z ) = 0, (2.3)
где z – координата электронного слоя.
Подставляя в это выражение E1 и Е2 из (2), получим
q1 z - q2( d – z)=0. (2.4)
Используя (2.1) и (2.4), найдем связь наведенных зарядов q1 и q2 с координатой электронного слоя z:
q1 = q(1 – z/d); q2=qz/d. (2.5)
Зависимость q1 и q2 от z линейная, при z=0, q1 = q и q2 = 0, а при z = d q1 = 0 и q2 = q. Вследствие движения слоя его координата z является функцией времени, при этом скорость слоя υ= dz/dt. Изменение зарядов q1 и q2 во времени означает, цепи течет ток
iнав = dq2 / dt = - dq1 / dt , (2.6)
называемый наведенным током.
Используя (2.6) и (2.5), получим
iнав = q υ /d (2.7)
Наведенный ток возникает, как только электронный слои появляется в промежутке между электродами, и исчезает, когда электронный слой достигает второго электрода. Длительность импульса наведенного тока равна времени пролета электронов. При постоянной скорости электронов (υ = const) импульс iнав был бы прямоугольным, при линейной зависимости скорости от времени – треугольным.
Используем (2.7) для нахождения наведенного тока во внешней цепи плоских электродов, если в пространстве между ними в рассматриваемый момент времени существует произвольное распределение плотности зарядов ρ(z, t), а не тонкий электронный слой. Применим (2.7) к бесконечно тонкому слою с толщиной dz и зарядом – dq, a затем произведем интегрирование. Наведенный ток, создаваемый элементарным слоем, по (2.7)
diнав(t) =dqυ(z,t)/d. (2.8)
Очевидно, что dq = ρ(z,t) S dz, поэтому из (2.8) получим 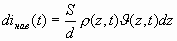 (2.9)
(2.9)
Создаваемый всеми электронными слоями в промежутке d в момент времени t наведенный ток
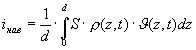 (2.10)
(2.10)
Подынтегральное выражение есть значение электронного тока в сечении z в момент времени t, связанное с переносом (конвекцией) электронов. Назовем его конвекционным током
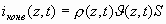 (2.11)
(2.11)
Подставляя (2.11) в (2.10), получим
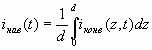 (2.12)
(2.12)
Если к электродам, показанным на рис. 1, приложить переменное напряжение u(t), то во внешней цепи кроме наведенного тока (2.12) будет существовать емкостный ток
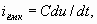 (2.13)
(2.13)
где C=ε0 S/d—емкость между электродами.
Поэтому полный ток в цепи
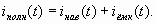 (2.14)
(2.14)
В (2.14) полный ток представлен как сумма наведенного и емкостного токов во внешней цепи, в отличие от обычного представления его суммой конвекционного тока (тока проводимости) и тока смещения, определяемых в зазоре между электродами:
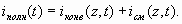 (2.15)
(2.15)
Выражение (12) позволяет вычислить наведенный ток во внешней цепи электродов, если известна зависимость конвекционного тока в зазоре от координаты и времени iконв(z,t). Наведенный ток в момент времени t равен усредненному по длине зазора значению конвекционного тока в этот момент времени. В частном случае, когда время пролета электронов много меньше периода переменного напряжения, можно считать, что iконв(z,t) практически не зависит от координаты и его можно вынести за знак интеграла. Тогда ![]() , т. е. наведенный ток совпадает с конвекционным. Поэтому в квазистатическом и статическом режимах нецелесообразно пользоваться понятием наведенного тока.
, т. е. наведенный ток совпадает с конвекционным. Поэтому в квазистатическом и статическом режимах нецелесообразно пользоваться понятием наведенного тока.
В лампах СВЧ период переменного напряжения сравним с временем пролета электронов, поэтому конвекционный ток iконв(z,t) в зазоре сильно зависит от координаты г и наведенный ток не равен конвекционному.
2.1. Работа триода на СВЧ
Анализ влияния времени пролета электронов существенно зависит от соотношения амплитуды переменных и постоянных напряжений на электродах. Если амплитуда много меньше постоянного напряжения, говорят о режиме малых амплитуд. Когда обе величины сравнимы, имеет место режим больших амплитуд.
В режиме малых амплитуд можно считать, что время пролета электронов практически определяется постоянными напряжениями на электродах, а пространственный заряд в области сетка – катод такой же, как в статическом режиме. Это позволяет создать сравнительно простую теорию электронных ламп СВЧ в режиме малых амплитуд.
Теоретическое рассмотрение схемы с общим катодом позволило сделать вывод, что влияние угла пролета электронов между электродами можно учесть введением комплексной крутизны лампы и активной входной проводимости. При этом модуль комплексной крутизны равен отношению амплитуды переменного тока в анодной цепи к амплитуде переменного напряжения на сетке, а ее фазовый угол показывает отставание анодного тока от сеточного напряжения. С ростом угла пролета, вызванного увеличением частоты или расстояния между электродами, фазовый сдвиг растет, а модуль крутизны уменьшается.
Появление активной проводимости входной цепи связано с тем, что из-за существования наведенного тока в цепи сетки появляется составляющая сеточного тока, совпадающая по фазе с переменным сеточным напряжением. В схеме включения с общим катодом входная активная проводимость примерно пропорциональна квадрату частоты.
Для уменьшения угла пролета в режиме малых амплитуд необходимо увеличивать положительное напряжение на электродах и использовать лампы с малым расстоянием между электродами.
Режим малых амплитуд характерен для усилителей слабого сигнала и для генераторов, работающих с очень низким КПД. Режим больших амплитуд используется в мощных усилителях и генераторах. В настоящее время маломощные электронные лампы СВЧ почти полностью вытеснены полупроводниковыми приборами СВЧ, а мощные электронные лампы применяются на частотах до 1 – 2 ГГц. Поэтому далее пойдет речь только о режиме больших амплитуд, который будет рассмотрен на примере схемы включения триода, показанной на рис. 2.2.
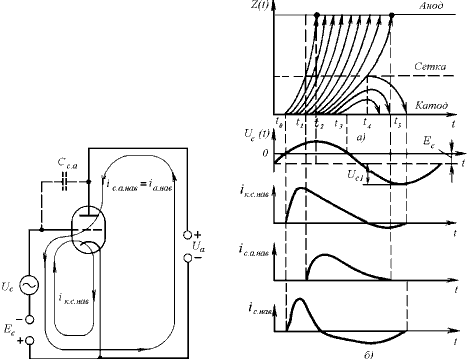
Теоретический анализ влияния времени пролета в триоде в режиме больших амплитуд весьма сложен. Однако представление о происходящих процессах можно получить с помощью пространственно-временных диаграмм, изображенных на рис. 3a. На этом рисунке z – координата электрона, отсчитываемая от катода, а t – время. Каждая кривая показывает зависимость координаты тонкого электронного слоя от времени. Кривые соответствуют разным моментам вылета электронов из катода. Переменное напряжение с амплитудой Uс1 и постоянное напряжение смещения сетки Ес<0 показаны внизу пространственно-временной Диаграммы. Мгновенное значение напряжения на сетке 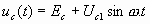
Каждая кривая строится по результатам решения уравнения движения электронов в лампе. Тангенс угла наклона касательной в любой точке пространственно-временной диаграммы определяет скорость электрона, необходимую для расчета наведенного тока.
Будем считать, что управляющая сетка настолько густа, что анод с потенциалом Ua не вызывает появления электрического поля в пространстве сетка - катод. Тогда движение электронов в этом пространстве будет определяться только напряжением на сетке Суммарное напряжение на сетке uc(t) проходит через нулевое значение (рис. 2.2, б) в моменты t0 и t3. Предположим, что лампа отпирается при суммарном напряжении Uc1>0, т. е. ток эмиссии существует в интервале времени t3 — t0 . Электрон, вылетевший из катода в момент времени t0 , будет двигаться к сетке в ускоряющем электрическом поле (uc > 0). И его скорость по мере приближения к сетке будет возрастать. В некоторый момент времени t1 первый электрон достигает сетки и входит в пространство сетка - анод, где имеется ускоряющее поле, так как напряжение на аноде Ua положительно и велико. Первый электрон попадает на анод в момент времени t2 .
На анод будут попадать также те из последующих электронов, вылетевшие из катода при положительном напряжении на сетке, которые подлетают к сетке с некоторой скоростью. Уменьшение скорости происходит вследствие уменьшения напряжения на сетке и изменения его знака после момента времени t3. Электрон, подошедший к сетке в момент времени t4 с нулевой скоростью (υ=dz/dt=0), начнет обратное движение к катоду, потенциал которого теперь выше потенциала сетки.
В момент времени t5 (рис. 2.2, б) на анод пришел последний электрон. Этот электрон прошел сетку в момент времени t4, позже которого электроны возвращаются к катоду. Таким образом, не все электроны, начавшие движение при положительном напряжении на сетке (uc>0), долетают до анода, часть их возвращается на катод. Чем больше время пролета электронов от катода до сетки (больше расстояние сетка – катод), тем больше электронов возвращается на катод.
С помощью пространственно-временной диаграммы, рассчитанной для большого числа электронов, отличающихся моментом вылета из катода, можно в любом- сечении лампы в любой момент времени определить число и скорость электронов, а следовательно, и конвекционный ток. Затем по (2.12) можно вычислить наведенный ток во внешней цепи электрода.
Как только первый электрон начинает в момент времени t0 движение от катода к сетке, во внешней цепи промежутка катод – сетка появляется наведенный ток iк.с.нав, текущий в этой цепи от катода к сетке (см. рис. 2.2). Ток iк.с.нав (см. рис. 3б) возрастает по мере .увеличения числа электронов в промежутке и достигает максимального значения. Последующее убывание тока связано с уменьшением скорости электронов, а затем с изменением ее направления. Электроны, начинающие движение к катоду, создают наведенный ток другого направления (от сетки к катоду во внешней цепи). В некоторый момент времени результирующий наведенный'' ток равен нулю, а затем меняет направление из-за возвращения электронов к катоду.
Аналогично наведенный ток iк.с.нав во внешней цепи промежутка сетка – анод появляется, когда электроны начинают поступать в этот промежуток через сетку. Этот ток растет, достигает максимального значения, убывает и обращается в нуль, когда последний электрон промежутка сетка – анод достигает анода в момент времени t5.
Проведенное приближенное рассмотрение показывает, что, если время пролета электронов сравнимо с периодом переменного напряжения, наведенный ток становится несимметричным по форме и имеет отрицательный выброс. Импульс наведенного тока в цепи анода не повторяет формы сеточного напряжения, а “затягивается” на значительную часть периода переменного напряжения, что вызывает уменьшение амплитуды первой гармоники анодного тока. Последнее приводит к снижению полезной мощности в нагрузке на частоте приложенного сигнала или на частоте генерируемых колебаний, если лампа используется в схеме генератора.
Зная наведенные токи iк.с.нав и iс.а.нав , можно, используя рис. 2, определить наведенные токи электронов: анодный ![]() , катодный
, катодный 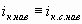 и сеточный
и сеточный 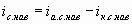 . Наведенный ток сетки iс.нав , равный сумме двух наведенных токов, текущих в сеточной цепи в противоположных направлениях, меняет свой знак в некоторый момент времени, когда токи iс.а.нав и iс.а.нав равны.
. Наведенный ток сетки iс.нав , равный сумме двух наведенных токов, текущих в сеточной цепи в противоположных направлениях, меняет свой знак в некоторый момент времени, когда токи iс.а.нав и iс.а.нав равны.
В тетроде на экранирующую сетку, расположенную между управляющей сеткой и анодом, подается положительное напряжение, сравнимое с анодным. Поэтому электроны, прошедшие через управляющую сетку, ускоряются в промежутке между сетками, и полное время пролета от управляющей сетки до анода уменьшается. Импульс анодного тока при этом менее растянут, а электронный КПД выше, чем в триоде.
2.2. Применение триодов и тетродов СВЧ
В диапазоне СВЧ более широко применяется схема включения триода с общей сеткой, а не с общим катодом, которая до сих пор рассматривалась. Упрощенная схема включения триода с общей сеткой, показанная на рис. 4, удобна для сравнения с упрощенной схемой триода с общим катодом (см. рис. 2). Промежуток лампы сетка–катод входит во входную цепь, а промежуток анод–сетка – в выходную цепь схемы, так что сетка является, обшей точкой этих цепей.
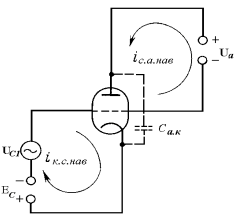
Рис. 2.3
Как видно из рис. 2.2 и 3.2, выходная (анодная) цепь связана с входной через емкость Сc.a в схеме с общим катодом и емкость Са.к в схеме с общей сеткой. Эта связь может привести к самовозбуждению лампы. Поскольку Са.к значительно меньше Са.с, то схема с общей сеткой более устойчива к самовозбуждению. Благодаря этому она широко применяется на высоких частотах. Недостатком схемы с общей сеткой является низкое входное сопротивление усилительного каскада (через входную цепь протекает весь переменный катодный ток лампы). Однако можно показать, что с увеличением частоты активная составляющая входной проводимости каскада с общей сеткой уменьшается из-за увеличения фазового сдвига между сеточным напряжением и первой гармоникой катодного тока. В то же время в схеме с общим катодом входная проводимость увеличивается с ростом частоты.
Требование уменьшения времени пролета в лампах СВЧ не является единственным. Необходимо также уменьшать междуэлектродные емкости, индуктивность вводов и диэлектрические потери в элементах лампы.
На частотах выше 500 МГц применяются триоды с дисковыми выводами: маячковые и металлокерамические. Рассмотрим для примера конструкцию генератора на маячковом триоде (рис. 2.4): 1, 2 – коаксиальные резонаторы в цепях сетка–катод и сетка–анод, 3 – петля связи, 4 – настроечные поршни, 5 – триод. Катод, сетка и анод плоские. Дисковые выводы становятся частью колебательной коаксиальной системы. Расстояние между электродами доходит до десятых и даже сотых долей миллиметра.
В металлокерамическом триоде вместо стекла используется специальная керамика. Диэлектрические потери в междуэлектродных изоляторах уменьшаются благодаря применению высокочастотной керамики с малыми диэлектрическими потерями. Современные миниатюрные металлокерамические триоды были разработаны на предельною частоту до 10 ГГц. Однако на таких частотах удалось получить очень небольшую мощность и низкий КПД.
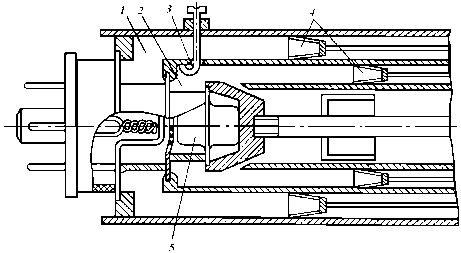
Рис 2.4
В качестве мощных генераторных ламп в длинноволновой части диапазона дециметровых волн применяются преимущественно триоды с водяным или воздушным охлаждением анодов, в конструкции которых учтены требования, предъявляемые к СВЧ лампам. В коротковолновой части диапазона дециметровых волн применяются мощные генераторные триоды, имеющие специальную конструкцию. Кольцевые вводы электродов этих ламп обладают значительно меньшими индуктивностью и омическим сопротивлением и позволяют легко соединить лампы с колебательной системой.
Металлические выводы ламп изготавливаются также из титана. Такие лампы называются титанокерамическими. Применение титана позволило улучшить характеристики приборов, так как при высоких температурах, развивающихся при их работе, титан обладает хорошими абсорбционными свойствами, т. е. поглощает выделяемые в лампе газы и в приборе поддерживается все время рабочий вакуум. Титанокерамические триоды имеют меньшие размеры, чем металлокерамические, при равных значениях выходной мощности.
Недостатком СВЧ триодов является низкий коэффициент усиления по мощности. Это обстоятельство привело к разработке тетродов. Электроды тетродов обычно имеют цилиндрическую конструкцию. Обе сетки, а иногда и катод составляются из большого числа стержней, расположенных по образующим цилиндров соответствующих радиусов. Динатронный эффект ослабляется использованием лучевой структуры электронного потока и удалением анода от экранной сетки, на сравнительно большое расстояние. В таких тетродах все электроды имеют дисковые выводы.
Для генерирования сверхмощных колебаний СВЧ диапазона конструктивное разделение лампы и колебательной системы из-за больших потерь в соединениях оказывается нерациональным. Поэтому электроды лампы изготавливаются вместе с колебательной системой, а резонаторные полости помещаются в вакуум. Примером может служить тетродный генератор, названный резнатроном, который в дециметровом диапазоне отдает среднюю мощность 50 – 70 кВт при КПД 60 – 65%. Напряжение источника питания составляет 10—16 кВ.
Дальнейшее развитие этого принципа конструирования ламп привело к созданию коакситрона. По существу коакситрон представляет собой цилиндрическую систему из 48 независимых элементарных триодов с общей сеткой, объединенных со входным и выходным резонаторами в одном вакуумном корпусе. Коакситрон имеет широкую рабочую полосу частот и высокую надежность. Прибор рекомендуется к использованию в широкодиапазонных многоканальных радиолокационных станциях. Коакситрон А15193 (США) является усилителем с коэффициентом усиления по мощности 13 дБ, рассчитанным на диапазон частот 400 – 500 МГц при уровне мощности в непрерывном режиме 150 кВт, а в импульсном – 10 МВт (КПД 43%). Разработаны коакситроны, перекрывающие диапазон частот 200 – 1300 МГц.
Триодные и тетродные генераторы обладают рядом достоинств по сравнению с другими генераторами СВЧ. Это сравнительно низкие питающие напряжения, отсутствие устройств для фокусировки электронного потока, достаточно высокий КПД в дециметровом диапазоне, сравнительно высокая стабильность частоты в генераторах и фазы в усилителях при изменении напряжения питания. Следует отметить также малую стоимость триодов. Основным недостатком триодных и тетродных генераторов является быстрое падение выходной мощности с ростом рабочей частоты. Практически они используются на частотах до 1,5 – 2 ГГц.
Тетроды СВЧ применяются в основном в выходных каскадах мощных передатчиков. Например, в телевизионном передатчике ЛАДОГА, предназначенном для черно-белого и цветного телевизионного вещания в диапазоне 470 – 622 МГц, в выходном каскаде используется металлокерамический тетрод ГС-17Б с выходной мощностью 7 кВт.
Триоды СВЧ применяются в качестве генераторов и усилителей средней мощности, а также в качестве преобразователей и умножителей частоты. В передатчике ЛАДОГА металлокерамический триод ГС-14Б работает усилителем-умножителем. Металлокерамические триоды и тетроды используются также в передатчиках радиорелейных линий связи с временным разделением и импульсной модуляцией.
В заключение следует заметить, что все время проводятся работы по усовершенствованию триодов и тетродов для телевизионных передатчиков. Фирма Сименс (ФРГ) разработала серию мощных тетродов для телевизионных передатчиков дециметрового диапазона, у которых благодаря использованию испарительно-конденсационного охлаждения выходная мощность в 2 раза выше, чем при воздушном охлаждении. Эти тетроды дешевле клистронов, эквивалентных им по параметрам. Анод тетродов имеет небольшие каналы охлаждения, ответвляющиеся от основного канала. В канале под давлением циркулирует вода, которая кипит и испаряется примерно при 120°C и охлаждает анод. Металлокерамический тетрод RS1034SK имеет выходную мощность 20кВт.
Контрольные вопросы.
1. Воздействие электрического и магнитного поля на движущийся заряд. Скорость электрона, время пролета, угол пролета.
2. Уточнение понятий “ток”. Наведенный ток. Зачем понадобилось введение этого понятия?
3. Отбор энергии у движущегося одиночного заряда и превращения ее в энергию СВЧ колебаний.
4. Особенности работы электронных ламп в диапазоне СВЧ. Основные факторы, влияющие на работу СВЧ триодов и тетродов.
3. Клистроны
3.1. Пролетный двухрезонаторный клистрон
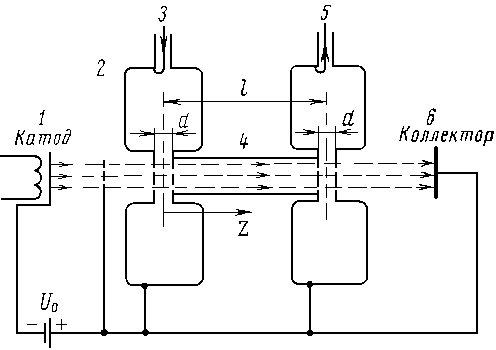 Рис. 3.1.
Рис. 3.1.
Принцип работы. Двухрезонаторный клистрон схематически изображен на рис. 3.1. В клистроне имеются два объемных резонатора с емкостными зазорами. Первый резонатор 3 называется входным, или модулятором, а второй 5 - выходным. Пространство 4 между ними называется пространством, дрейфа или группирования, Электроны эмитируемые катодом 1, ускоряются постоянным напряжением U0 электрода 2 и попадают в узкий зазор между сетками первого резонатора. Между ними имеется продольное высокочастотное электрическое поле, которое периодически ускоряет и замедляет электроны, т. е. модулирует скорость электронов.
В пространстве дрейфа быстрые электроны догоняют медленные, обеспечивая группирование электронов, т. е. преобразование модуляции электронного потока по скорости в модуляцию по плотности. Модулированный электронный поток поступает во второй резонатор и создает в нем наведенный ток, протекающий по внутренней поверхности его стенок. В резонаторе возникают колебания, а между его сетками появляется электрическое высокочастотное поле, которое должно вызывать торможение сгруппированных электронов. В выходном резонаторе кинетическая энергия тормозящихся электронов преобразуется в энергию СВЧ колебаний. Электроны, прошедшие через второй резонатор и отдавшие СВЧ полю часть своей кинетической энергии, попадают на коллектор 6, где рассеивают оставшуюся часть кинетической энергии в виде тепла. Проанализируем подробнее процессы в пролетном клистроне.
Скоростная модуляция электронов. К сетке резонатора (см. рис. 3.1) все электроны подлетают с одинаковой скоростью, определяемой ускоряющим напряжением
![]() (3.1)
(3.1)
где е и т — заряд и масса электрона.
Пусть между сетками входного резонатора приложено переменное напряжение U1sinωt Скорость электрона после прохождения зазора между сетками может быть определена решением уравнения движения
![]() (3.2)
(3.2)
где напряженность переменного поля в зазоре с расстоянием между сетками d равна Е=[U1 sin(ut)]/d. Будем считать, что амплитуда напряжения U1 мала (U1/U2<<1), т. е. мало изменение скорости электронов. В этом случае время пролета всех электронов через зазор практически одинаково и составляет 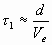 . Обозначим t1 момент прохождения электроном середины зазора. Тогда t1 – τ1/2 - момент входа в зазор; t1 + τ1/2 —момент выхода. Скорости электрона в эти моменты времени равны Ve и V соответственно. Решая при указанных граничных условиях, дифференциальное уравнение (3.2), получим скорость электрона при выходе из резонатора
. Обозначим t1 момент прохождения электроном середины зазора. Тогда t1 – τ1/2 - момент входа в зазор; t1 + τ1/2 —момент выхода. Скорости электрона в эти моменты времени равны Ve и V соответственно. Решая при указанных граничных условиях, дифференциальное уравнение (3.2), получим скорость электрона при выходе из резонатора
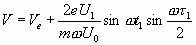
Используя условие U1/U2<<1, можно преобразовать эту формулу:
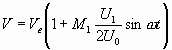 (3.3)
(3.3)
где М1=(sin0,5θ1)/0,5θ1 – коэффициент эффективности электронного взаимодействия или коэффициента связи электронного пучка с полем зазора; θ1=ωτ1 - угол пролета электронов в зазоре.
Зависимость коэффициента М1 от угла пролета показана на рис. 3.2. Уменьшениеθ1 путем сближения сеток нецелесообразно из-за роста емкости резонатора и снижения благодаря этому его эквивалентного сопротивления. Типичные значения угла пролета лежат в пределах π/2 - π. Физический смысл коэффициента М1 заключается в том, что он учитывает уменьшение глубины модуляции скорости при конечном угле пролета по сравнению с идеальным случаем бесконечного малого угла.
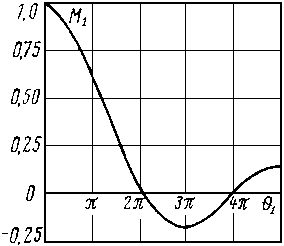
Рис. 3.2
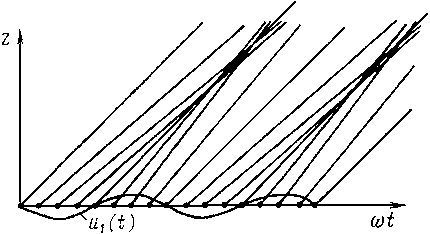 рис. 3.3
рис. 3.3
Группирование электронов. Рассмотрим пространственно-временную диаграмму электронов в двухрезонаторном клистроне, изображенную на рис. 3.3. По вертикальной оси отложено расстояние г в пространстве дрейфа, а по горизонтальной — время. В нижней части рисунка изображено переменное высокочастотное напряжение u1(t) на сетках входного резонатора. Будем считать движение электронов в пространстве дрейфа равномерным со скоростью, определяемой (3.3). Такой “кинематический” анализ группировки дает наглядное представление о механизме процессов и объясняет его основные закономерности. График движения каждого электрона определяется скоростью электрона. [Пространственно-временные диаграммы для электронов на пути от катода до резонатора (z<0) на рис. 3.3 не показаны.] Точки пересечения прямых с осью времени определяют входную фазу электронов в пространстве дрейфа относительно напряжения на зазоре первого резонатора. Считаем, что электроны скачкообразно изменяют свою скорость в момент прохождения центра зазора. Диаграмма наглядно показывает, что в потоке электронов образуются сгустки и разрежения. Для тех электронов, которые проходят высокочастотное поле, когда оно тормозящее, наклон прямых уменьшается, для других - увеличивается. В результате прямые расходятся или сходятся, чем объясняются группирование или фазовая фокусировка электронов. Последнее название объясняется аналогией с геометрической фокусировкой пучка света в оптике. В каждом периоде колебаний образуется один сгусток, в центре которого находится электрон, прошедший через зазор без изменения скорости, т. е. в момент перехода поля через нуль от тормозящего к ускоряющему полупериоду.
Группирование было бы идеальным, если бы все электроны, прошедшие через первый резонатор за полупериод, приходили ко второму резонатору одновременно. В этом случае конвекционный ток в сечении второго резонатора представлял бы периодическую последовательность δ-импульсов. Однако при синусоидальной скоростной модуляции группирование отличается от идеального. Рассмотрим, какая существует связь при синусоидальной скоростной модуляции между моментами прихода электронов t2 во второй резонатор и моментом t1 прохождения их через первый. Очевидно, что
![]() (3.4)
(3.4)
где l—длина пространства дрейфа (см. рис. 3.1).
Подставляя (3.3) в (3.4), получим
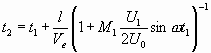 .
.
В усилительных клистронах амплитуда входного напряжения U1 много меньше U0(U1<<U0), поэтому, раскладывая в ряд по малому параметру MU1/2U0 и оставляя в нем два первых члена, получим
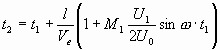 .
.
Умножая обе части уравнения на со, получим
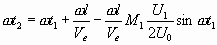 (3.5)
(3.5)
Введем обозначение
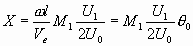 (3.6)
(3.6)
— параметр группирования; θ0=ω/Ve — средний угол пролета в пространстве дрейфа, равный углу пролета электрона, не изменившего своей скорости при прохождении первого резонатора (невозмущенный электрон). Угол пролета 6о называют также невозмущенным углом пролета.
Соотношение (3.5) можно с учетом (3.6) записать
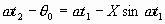 (3.7)
(3.7)
Это уравнение определяет фазу прибытия ωt2 электрона ко второму зазору. Если отсутствует модулирующее напряжение (U1=0), то X=0. В этом случае ωt2-θ0=ωt1 и фаза прибытия электрона во второй зазор линейно связана с фазой прохождения его через первый зазор. Электроны не группируются, и имеет место только одинаковое запаздывание всех электронов по фазе. Зависимость величины (ωt2-θ0 ω), характеризующей фазу появления электрона в зазоре второго резонатора, от фазы прохождения через зазор первого резонатора приведена на рис. 3.4.Чем больше параметр группирования, тем сильнее кривые отклоняются от прямой линии, соответствующей значению Х=0.
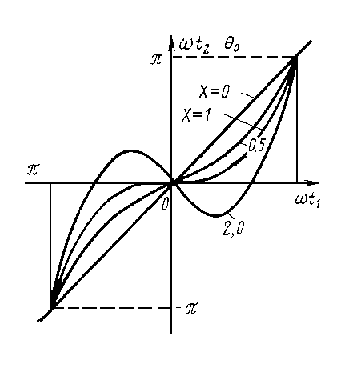 Рис. 3.4
Рис. 3.4
Идеальному группированию, т. е. одновременному приходу электронов на рис. 3.4 соответствует ступенчатая функция. Следовательно, группирование электронов в двухрезонаторном клистроне сильно отличается от идеального. Рассмотрим способ определения формы импульсов конвекционного тока.
Конвекционный ток. Пусть через входное сечение трубки дрейфа проходит группа электронов с зарядом Δq1 за время Δt1. В этом сечении конвекционный ток
i1= Δq1/ Δt1 (3.8)
Аналогично в выходном сечении трубки дрейфа конвекционный ток
i2= Δq2/ Δt2 (3.9)
где Δq2 - заряд группы электронов, пролетающих выходной резонатор за время Δt2.
Если рассматривается одна и та же группа электронов, а перехват электронов в трубке дрейфа отсутствует, то
Δq1=Δq2 (3.10)
Используя (3.8), (3.9) и (3.10), получим
![]() (3.11)
(3.11)
или
![]() (3.12)
(3.12)
Ток i1 равен постоянному току I0, так как в первом резонаторе еще не происходит группирования электронов. Производную в. (3.12) можно определить из (3.7):
dt2/dt1=1 - X cos ωt1 (3.13)
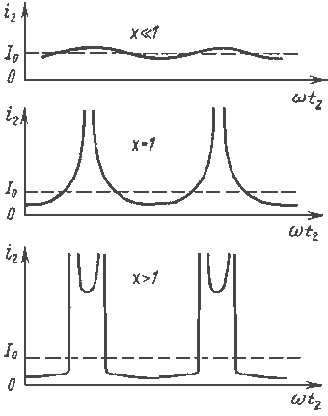 Рис. 3.5.
Рис. 3.5.
Зависимости конвекционного тока от времени t2 при нескольких значениях параметра группирования Х показаны на рис. 3.5. Ток i2 обращается в бесконечность при значениях t2, для которых производная (3.13) dt2/dt1=0. На рис. 3.4 при Х=1 нулевая производная имеется только в одной точке ωt1=0, а при Х >1 - в двух. С увеличением Х интервал времени и провал между бесконечными пиками тока увеличиваются.
Ток i2 является периодической несинусоидальной функцией времени и может быть представлен рядом Фурье [3]:
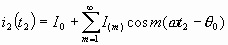 (3.14)
(3.14)
где амплитуда гармоники тока с номером m
![]() (3.15)
(3.15)
выражается через функции Бесселя первого рода т-го порядка. Выражения (3.14) и (3.15) справедливы при любых значениях параметра группирования.
Через зазор выходного резонатора проходит сгруппированный поток электронов и наводит в нем ток. Если выходной резонатор настроен на частоту модулирующего напряжения ц”, то мощность в нем будут создавать только колебания этой частоты и напряжение между его сетками будет практически синусоидальным. Следовательно, из членов ряда (3.14) можно взять только первую гармонику электронного тока, амплитуда которой
![]() (3.16)
(3.16)
Максимальное значение амплитуды первой гармоники соответствует максимуму функции Бесселя J1(X), т. е. получается при Х=1,84:
![]() (3.17)
(3.17)
Так как в клистроне длина пространства дрейфа l фиксирована, а напряжение питания U0 определено паспортными данными, то параметр группирования (3.6) можно регулировать изменением амплитуды входного сигнала U1.
Наведенный ток и электронная мощность. Вычисление амплитуды первой гармоники наведенного тока по
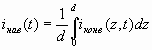
приводит к следующему результату:
Iнав(1)=M2I(1) (3.18)
где M2 — коэффициент электронного взаимодействия во втором резонаторе, аналогичный коэффициенту M1 в (3.3). В выходном резонаторе, настроенном на частоту сигнала, с учетом (3.18) и (3.16) электронная мощность
P= Iнав(1)U2/2=M2U2I0J1(X) (3.19)
Потребляемая клистроном мощность P0=I0U0, поэтому электронный КПД
ηэ=P/P0=M2J1(X)U2/U0 (3.20)
Электронная мощность (3.19) растет при увеличении тока I0 и напряжения на выходном резонаторе U2. Обычно для оценки максимальной мощности и электронного КПД принимают ![]() . Ограничение напряжения объясняется следующим образом. Средняя кинетическая энергия электронов, входящих в резонатор, определяется ускоряющим напряжением и равна eU0. Если предположить, что амплитуда напряжения U2>U0, то кинетическая энергия некоторых электронов будет недостаточна для преодоления тормозящего действия поля в зазоре резонатора. Эти электроны вернутся обратно в пространство дрейфа, что приведет к уменьшению мощности колебаний в резонаторе.
. Ограничение напряжения объясняется следующим образом. Средняя кинетическая энергия электронов, входящих в резонатор, определяется ускоряющим напряжением и равна eU0. Если предположить, что амплитуда напряжения U2>U0, то кинетическая энергия некоторых электронов будет недостаточна для преодоления тормозящего действия поля в зазоре резонатора. Эти электроны вернутся обратно в пространство дрейфа, что приведет к уменьшению мощности колебаний в резонаторе.
Определяемый из (3.20) при ![]() максимальный электронный КПД
максимальный электронный КПД
ηэ max=J1(X) (3.21)
Самое большое теоретическое значение ηэ будет при X=1,84:
ηэ пред=0,58.
Полный КПД клистрона, учитывающий потери в колебательной системе, потерю электронов на сетках резонаторов и другие факторы, гораздо меньше и составляет 15—20%.
Оптимальное значение параметра группирования X, обеспечивающее максимальный КПД клистрона, оказывается больше единицы, и оптимальная форма импульса конвекционного тока в двухрезонаторном клистроне при синусоидальной модуляции должна содержать два пика (рис. 3.5, снизу).
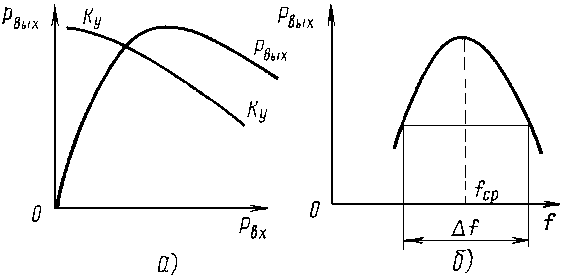
Рис. 3.6
Рассмотрим амплитудную (рис. З.6а) и амплитудно-частотную (рис. 3.6 б) характеристики пролетного клистрона. Выходная мощность вначале линейно растет с увеличением Рвх, а затем наступает насыщение. Максимальное значение выходной мощности достигается при X=1,84. Коэффициент усиления Ку максимален на линейном участке характеристики (при X<<1) и при увеличении Pвх уменьшается.
Увеличению коэффициента усиления в двухрезонаторном клистроне препятствует влияние пространственного заряда, мешающего группированию электронов. Расталкивание одноименно заряженных электронов в сгустке приводит к увеличению скорости электронов, летящих перед центральным электроном, и к уменьшению ее у остальных. Группирование в пролетном клистроне возможно, если спереди летят медленные, а сзади быстрые электроны (см.§3.1). Продольные силы расталкивания приводят на некотором расстоянии к выравниванию скоростей электронов сгустка, что эквивалентно уменьшению глубины скоростной модуляции и значения параметра группирования. Это ограничивает коэффициент усиления двухрезонаторного клистрона. При заданном режиме работы существует определенная длина трубки дрейфа, соответствующая максимальному коэффициенту усиления. Его значение мало и обычно составляет 10—15 дБ. Кроме того, двухрезонаторный клистрон — это узкополосный усилитель, так как в нем используются высокодобротные резонаторы. Относительная полоса пропускания обычно несколько десятых процента. По этим причинам двухрезонаторные усилительные клистроны практически не используются. Значительное расширение полосы пропускания, увеличение коэффициента усиления и КПД достигнуты в многорезонаторных клистронах, которые будут рассмотрены ниже.
3.2. Двухрезонаторные клистронные генераторы
Рассмотрим схему двухрезонаторного клистронного генератора (рис. 3.7).
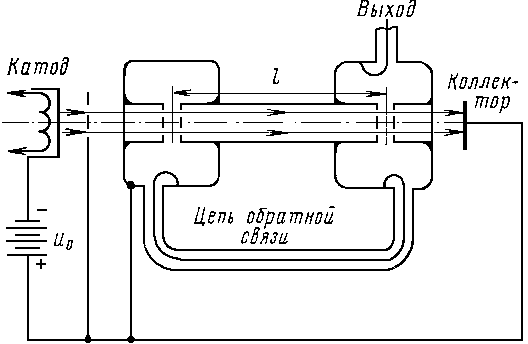 Рис. 3.7
Рис. 3.7
Между входным и выходным резонаторами клистронного генератора есть цепь обратной связи. Для самовозбуждения клистрона и поддержания стационарных колебаний необходимо выполнить баланс фаз и баланс амплитуд.
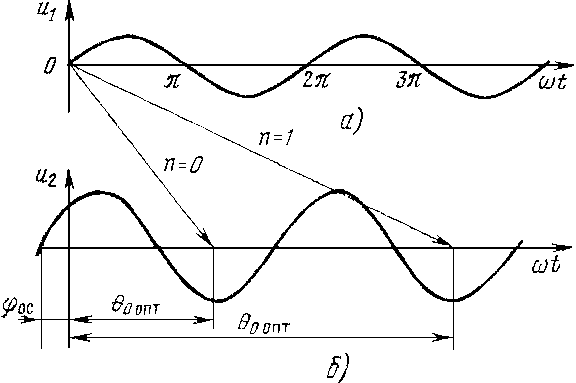 Рис. 3.8
Рис. 3.8
Рассмотрим кривые напряжений на зазоре входного (рис, 3.8а) и выходного (рис. 3.8б) резонаторов клистронного генератора. Сдвиг фазы в цепи обратной связи. Для отдачи максимальной энергии сгустки электронов должны проходить выходной резонатор в момент максимального тормозящего поля. Центром сгустка будет электрон, который проходит первый зазор в момент перехода от тормозящего поля к ускоряющему. Из рис. 3.8 видно, что в этом случае оптимальный угол пролета в пространстве дрейфа при наличии запаздывания на угол φо.с в линии обратной связи θ0 опт+φо.с=2π(n+3/4).
Так как угол пролета между резонаторами, введенный в (3.6),
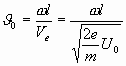 ,
,
то, считая 6о=0оопт, получим
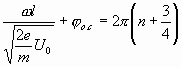 (3.22)
(3.22)
Существует множество дискретных областей значений U0, в которых возможны автоколебания. Эти области называются зонами генераций.
При вариациях ускоряющего напряжения U0 в пределах зоны для выполнения баланса фаз автоматически должна изменяться частота колебаний. Это явление называется электронной перестройкой частоты.
Вторым необходимым условием самовозбуждения двухрезонаторного клистрона является баланс амплитуд. Клистрон может генерировать колебания только в том случае, если ток электронного луча /о превосходит некоторое определенное значение, называемое пусковым током. При токе, меньшем пускового, электронный луч передает в выходной резонатор энергию, не достаточную для покрытия потерь во входном и выходном резонаторах.
Максимальная выходная мощность и КПД клистронных генераторов такие же, как в двухрезонаторных пролетных усилителях. В настоящее время они находят сравнительно узкое применение как генераторы средней мощности самой коротковолновой части сантиметрового диапазона и в миллиметровом диапазоне, где создание полупроводниковых генераторов соответствующей мощности затруднено. Основное назначение клистронных генераторов—получение колебаний высокой стабильности. Для повышения стабильности частоты в цепь обратной связи включают высокодобротную колебательную систему (один или несколько резонаторов). Клистронные генераторы используются в диапазоне частот 5,5—44 ГГц. Их выходная мощность лежит в пределах 0,2—200 Вт. Они применяются в системах связи, доплеровской радиолокации, радиомаяках, а также для накачки параметрических усилителей.
3.3. Многорезонаторные клистроны
Принцип работы. Двухрезонаторные клистроны не обеспечивают больших коэффициентов усиления и КПД. Для достижения большого усиления можно применять последовательное соединение нескольких клистронов, однако гораздо выгоднее использовать многорезонаторные клистроны, которые имеют большой коэффициент усиления и высокий КПД.
Рассмотрим особенности работы многорезонаторных клистронов на примере трехрезонаторногоМежду входным 1 и выходным 3 резонаторами располагается еще один промежуточный ненагруженный резонатор 2.
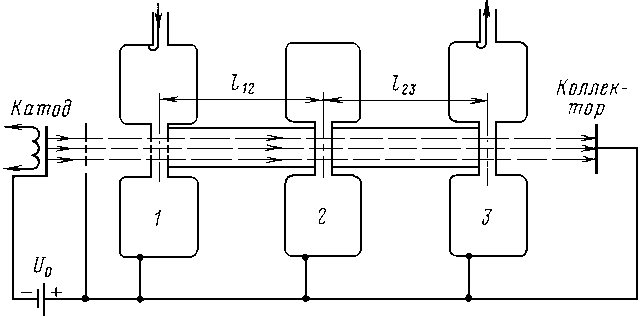
Рис. 3.9
Схема выгоднее, чем усилитель из двух двухрезонаторных клистронов, так как в ней необходим только один электронный пучок, что позволяет сократить мощность источников питания. Кроме того, из-за уменьшения числа резонаторов упрощается их настройка и снижаются потери.
Возможность увеличения коэффициента усиления удобно пояснить на пространственно-временной диаграмме
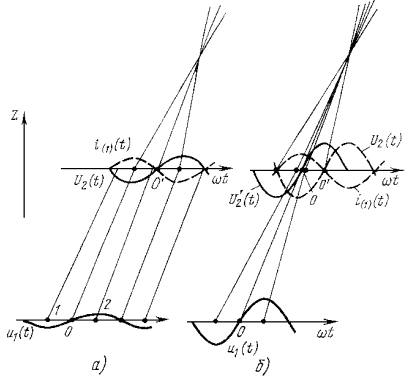
Рис. З.10а.
Рассмотрим случай, когда все резонаторы настроены на частоту сигнала (синхронная настройка). Как и в двухрезонаторном клистроне, во входном резонаторе многорезонаторного клистрона электроны модулируются по скорости. В пространстве дрейфа между входным и промежуточным резонаторами происходит группирование электронного потока, однако при слабом входном сигнале оно незначительно: электроны 1 и 2 (см. рис. З.10а) лишь немного смещаются по направлению к невозмущенному электрону О. Из-за малого параметра группирования амплитуда первой гармоники конвекционного тока i(1), Изображенного штрихпунктирной кривой, в сечении z2 промежуточного резонатора будет также небольшой. Так как промежуточный резонатор не нагружен и является высокодобротным, то даже при малой амплитуде конвекционного тока напряжение U2, создаваемое наведенным током, будет большим. Это напряжение вызывает сильную модуляцию скорости электронов, пролетающих через промежуточный резонатор. Следовательно, во втором пространстве дрейфа (между вторым и третьим резонаторами) произойдет основное группирование электронов. При синхронной настройке напряжение во втором резонаторе U2(t) противоположно по фазе первой гармонике конвекционного тока i(1). Для второго резонатора электрон О', приходящий позже электрона О, будет невозмущенным, около него должно происходить основное группирование. Поэтому распределение электронов в сгустке при слабом входном сигнале практически будет определяться этим резонатором и зависимость конвекционного тока в третьем резонаторе от времени будет примерно такой же, как в двухрезонаторном клистроне, образованном вторым и третьим резонаторами, но при модуляции скорости напряжением U2. Однако коэффициент усиления в трехрезонаторном клистроне сильно увеличивается, так как группирование электронов получается при существенно меньшей мощности сигнала, подводимой к входному резонатору.
Проведенное рассмотрение объясняет возможность получения большого коэффициента усиления в трехрезонаторном клистроне. Однако максимальное значение амплитуды первой гармоники конвекционного тока, а следовательно, максимальные выходная мощность и электронный КПД, получаемые в оптимальном режиме при синхронной настройке, остаются практически такими же, как в двухрезонаторном клистроне, и предельное теоретическое значение КПД составляет 58%.
Для увеличения КПД в многорезонаторных клистронах производится расстройка тех промежуточных резонаторов, на которых велико переменное напряжение, создаваемое наведенным током. Поясним это с помощью пространственно-временной диаграммы на рис. 3.10б. Входной сигнал u1(t) взят достаточно большим, чтобы обеспечить при синхронной настройке резонаторов хорошее группирование электронов. Первая гармоника конвекционного тока в сечении второго резонатора i(1)(t) проходит через амплитудное значение в момент прихода центрального электрона сгустка О. Существенно, что во втором резонаторе этот электрон перестает быть невозмущенным, так как таким становится электрон О', приходящий на четверть периода позже, когда u2(t)=0. Значительное смещение центра сгустка на рис. 3.10б относительно нового центра группирования О' не позволяет электронам сгустка эффективно сгруппироваться около электрона О', а следовательно, не позволяет получить возможные максимальные значения амплитуды первой гармоники тока и электронного КПД.
Если же центральный электрон сгустка О придет во второй резонатор в момент нулевого напряжения u2(t), то он останется невозмущенным. Тогда к пришедшему сгустку будут симметрично догруппировываться другие электроны, что вызовет увеличение числа сгруппированных электронов и амплитуды первой гармоники тока. Такое "совмещение" электронов О и О' можно получить, создавая между напряжением и током i(1)(t) сдвиг фазы 90°. На рис. 3.10б напряжение u2(t) соответствует синхронной настройке, когда U2{t) и i(1)(t) противоположны по фазе, a u'2{t) соответствует сдвигу фазы 90°. Такой сдвиг фазы возможен при очень большой расстройке второго резонатора относительно частоты сигнала в сторону более высоких частот. Однако при этом из-за уменьшения эквивалентного сопротивления резонатора напряжение между сетками станет настолько малым, что даже приведет к ухудшению группирования. Поэтому приходится создавать сдвиг фазы меньше 90°, а уменьшение напряжения компенсировать соответствующим увеличением амплитуды входного сигнала или введением дополнительных промежуточных резонаторов.
Теоретические расчеты показывают, что в трехрезонаторном клистроне по сравнению с двухрезонаторным можно увеличить амплитуду первой гармоники конвекционного тока до значения, при котором электронный КПД достигает 75%. Дальнейшее увеличение числа резонаторов не приводит к значительному росту электронного КПД, но увеличивает коэффициент усиления и изменяет амплитудно-частотную характеристику. Наиболее распространены четырех — шестирезонаторные клистроны.
Параметры и характеристики. Максимальный коэффициент усиления трехрезонаторного клистрона достигает примерно 35 дБ вместо 15 дБ в двухрезонаторном клистроне. Теоретически можно создать клистронный усилитель с любым коэффициентом усиления. Однако по мере возрастания числа резонаторов, т. е. увеличения числа каскадов усиления, труднее исключить самовозбуждение усилителя из-за наличия паразитной обратной связи. Коэффициент усиления N-резонаторного клистрона можно ориентировочно определить с помощью следующего эмпирического соотношения, в децибелах
Kу (P)=15+20(N-2). (3.23)
Амплитудные характеристики [зависимость Pвых=f(Pвх)] многорезонаторного клистрона приведены на рис. 3.11.
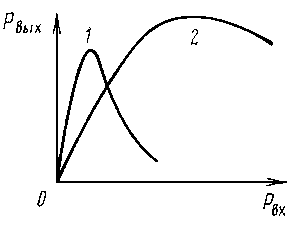 Рис. 3.11
Рис. 3.11
Вид характеристик изменяется в зависимости от настройки промежуточных резонаторов. Кривая 1 соответствует режиму синхронной настройки резонаторов, а кривая 2 режиму получения максимальных мощности и КПД. Начальный участок характеристики 1 имеет большую крутизну, и она достигает максимума при малой входной мощности Pвх. Затем при увеличении Рвх выходная мощность резко падает. Эта характеристика соответствует режиму максимального коэффициента усиления. Кривая 2 соответствует расстройке промежуточных резонаторов. Она имеет более пологий начальный участок, что свидетельствует о малом коэффициенте усиления клистрона. Область насыщения—более широкая. Благодаря лучшим условиям группирования в этом режиме достигается большая выходная мощность и выше значение электронного КПД.
Ширина полосы пропускания многорезонаторного клистрона в режиме синхронной настройки в основном определяется добротностью резонаторов. При расстройке резонаторов полоса пропускания увеличивается. Путем расстройки резонаторов относительно средней частоты полосы пропускания и подбора их добротностей удается синтезировать амплитудно-частотную характеристику и расширить полосу усиливаемых частот до нескольких процентов при уменьшении коэффициента усиления и выходной мощности.
На рис. 3.12 приведена частотная зависимость КПД мощного широкополосного четырехрезонаторного усилительного клистрона. Цифры 1—4 соответствуют собственным частотам резонаторов.
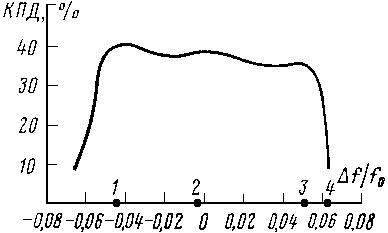 Рис. 3.12
Рис. 3.12
Для оценки искажений широкополосных сигналов, усиливаемых клистроном, необходимо знать также фазовые характеристики, определяющие зависимость разности фаз между колебаниями на входе и выходе от различных факторов, например от ускоряющего напряжения и амплитуды входного сигнала. Ускоряющее напряжение влияет на угол пролета электронов, а увеличение сигнала приводит к асимметрии формы сгустка и, следовательно, к изменению фазового сдвига первой гармоники тока, возбуждающей выходной резонатор.
3.4. Применение многорезонаторных клистронов
Многорезонаторные клистроны можно разделить на клистроны непрерывного действия и импульсные. Многорезонаторные клистроны широко применяются в выходных каскадах мощных передатчиков дециметровых и сантиметровых волн. Большое усиление, свойственное таким клистронам, позволяет использовать маломощные входные каскады, энергетические показатели которых незначительно влияют на общий КПД передатчика. Характеристики передатчика в основном определяются характеристиками оконечного каскада на клистроне.
Обычно клистроны в непрерывном режиме применяются в качестве передатчиков тропосферной связи с уровнями мощности 1—20 кВт и систем связи "Земля—спутник" с уровнями мощности до 50 кВт. Клистроны непрерывного режима работы мощностью от 50 до 500 кВт (сверхмощные) применяются для передатчиков радиолокационных станций и станций управления на межпланетных расстояниях. Клистроны для телевизионных передатчиков работают на уровнях мощности до 50 кВт*. В установках промышленного нагрева используются мощности от 1 до 50 кВт.
Многорезонаторные усилительные клистроны получили широкое распространение в качестве оконечных импульсных усилителей в передатчиках радиолокационных станций с мощностью в импульсе до 200 кВт. Сверхмощные импульсные клистроны (от 200 кВт до 30 МВт) применяются в ускорителях заряженных частиц и в системах сверхдальней локации. Коэффициент полезного действия мощных клистронов уже достигает 70 - 80% в дециметровом диапазоне. Поэтому все больший интерес приобретает проблема передачи энергии в свободном пространстве с помощью колебаний СВЧ диапазона.
В клистронных передатчиках практически возможны все виды модуляции. В многоканальных передатчиках для тропосферной связи используются как частотная, так и амплитудная модуляции. При передаче телевизионного сигнала по тропосферным радиорелейным линиям применяется частотная модуляция. В вещательных телевизионных передатчиках на клистроне используется амплитудная модуляция, а в радиолокационных — импульсная. В клистронных передатчиках модуляция может осуществляться либо в возбудителе до клистрона и тогда клистрон является только усилителем модулированных колебаний, либо непосредственно в самом клистроне. В последнем случае на вход клистрона подаются немодулированные колебания.
Для фокусировки электронного потока чаще всего используют постоянное магнитное поле соленоида. Однако фокусирующие системы такого типа громоздки и имеют большую массу. Например, клистрон непрерывного действия мощностью 50 кВт для телевизионного передатчика имеет длину примерно 1,8 м я массу 90 кг. Масса фокусирующей системы 270 кг. Перспективнее применять периодическую фокусировку с использованием как электростатических, так и магнитных линз, это позволяет уменьшить массу приборов. В настоящее время стали широко применяться для фокусировки постоянные магниты из высококоэрцитивных самарий- кобальтовых сплавов, что позволило существенно уменьшить массу и габариты клистронов.
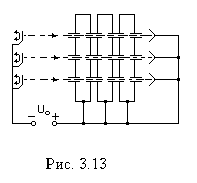
Для снижения ускоряющего напряжения были разработаны многолучевые клистроны (рис. 3.13). Каждый электронный поток взаимодействует с СВЧ полем общих резонаторов. Многолучевой клистрон может быть предназначен также для получения большой мощности при заданном рабочем напряжении.
В оконечных каскадах усилителей мощности в современном телевизионном передатчике ИЛЬМЕНЬ, работающем в дециметровом диапазоне с выходной мощностью 20 кВт, использованы мощные четырех резонаторные клистроны [II].
Большой интерес представляют клистроны с распределенным взаимодействием, конструкция которых отличается тем, что выходной резонатор многорезонаторного клистрона (а иногда и промежуточные резонаторы) заменен системой из двух или нескольких связанных резонаторов. Получается многозазорный резонатор, с полей которого взаимодействует электронный поток. Клистроны с распределенным взаимодействием имеют более высокий КПД, а также более высокое произведение коэффициента усиления на ширину полосы частот.
Развитие клистронов в ближайшие годы будет иметь некоторые особенности. Так, клистроны начинают оценивать не по выходным параметрам и характеристикам, а в совокупности с устройствами, необходимыми для эксплуатации. В связи с этим проводятся исследования по уменьшению массы магнитной фокусирующей системы, которая во многих случаях на порядок тяжелее клистрона - ведутся работы по снижению напряжения и тока управляющей сетки, вводимой в импульсный клистрон, так как это снижает габариты, массу и мощность модулятора, без которого не может работать импульсный клистрон. Большое внимание уделяется повышению надежности и долговечности. Разрабатываются устройства, предохраняющие мощные клистроны от случайного и преждевременного выхода из строя во время эксплуатации. Для систем тропосферной и космической связи создаются клистроны с программированной механической перестройкой резонаторов на ряд фиксированных частот при относительно узкой ширине полосы пропускания, но с большой выходной мощностью и КПД.
3.5. Отражательный клистрон
Принцип работы. Отражательные клистроны (рис. 3.14) предназначены для генерирования СВЧ колебаний малой мощности.
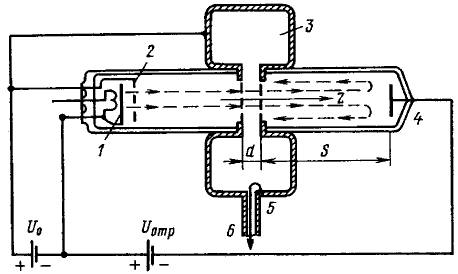 Рис. 3.14
Рис. 3.14
Клистрон имеет только один объемный резонатор 3, который должен выполнять две функции: модулировать скорость электронов и отбирать СВЧ энергию от модулированного по плотности электронного потока. За резонатором расположен отражатель 4 — электрод, на который относительно катода 1 подано отрицательное напряжение Uотр. Мощность колебаний, генерируемых клистроном, выводится из резонатора с помощью петли связи 5, переходящей в коаксиальную линию 6. Скорость электронов перед резонатором определяется напряжением U0 ускоряющего электрода 2.
Рассмотрим движение электронов с помощью пространственно-временной диаграммы (рис. 3.15).
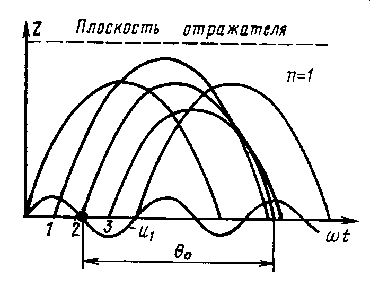 Рис. 3.15
Рис. 3.15
Пусть в режиме стационарных колебаний между сетками резонатора существует напряжение u1(t). Электроны, ускоренные напряжением U0, входят в зазор резонатора, модулируются по скорости электрическим полем этих колебаний и поступают в пространство между резонатором и отражателем. Так как на отражатель подано отрицательное постоянное напряжение, электроны попадают в тормозящее электростатическое поле. Когда скорость электронов уменьшится до нуля, они начнут обратное движение к резонатору под действи того же электростатического поля, которое для них теперь является ускоряющим.
В результате движения электронов от резонатора к отражателю и обратно происходит их группирование. Электронные сгyстки образуются относительно невозмущенных электронов 2, выходящих из резонатора в момент времени, когда u1=0 при переходе от ускоряющего к тормозящему полупериоду СВЧ напряжения. Электрон 1, вышедший раньше и имеющий большую скорость, проникает в тормозящее поле на большее расстояние z, т. е. летит большее время, чем электрон 2, и может вернуться в зазор почти одновременно с ним. Электрон 3, выйдя из зазора позже электрона 2 и с меньшей скоростью, проникает в тормозящее поле на меньшее расстояние. Из-за уменьшения времени пролета он может вернуться в резонатор почти одновременно с электроном 2. На этом различии времен пролета ускоренных и замедленных электрон основано группирование электронного потока в отражательно клистроне.
Сгруппированный электронный поток должен возвращаться в резонатор в пределах того полупериода СВЧ напряжения на зазоре, который оказывает тормозящее действие. Тогда он отдаст часть своей кинетической энергии высокочастотному полю резонатора и поддерживает колебания в резонаторе (положительная обратная связь). Следует заметить, что полупериод, названный ускоряющим для электронов, идущих от катода, одновременно будет тормозящим для электронов, возвращающихся в резонатор под действием напряжения на отражателе.
Если электрон возвращается в резонатор при амплитудном значении тормозящего поля, то отдаваемая им кинетическая энергия максимальна. Очевидно, что сгусток отдаст наибольшую энергию СВЧ полю, если центральный его электрон (невозмущенный) приходит в момент максимума поля. Следовательно, как видно из рис. 3.15, для обеспечения этого требования для невозмущенного электрода угол пролета
Оо опт=2πn+3/4), (3.24)
где n=0, 1, 2, ...— целое число, называемое номером зоны генерации, Оо опт — оптимальный угол пролета невозмущенного электрона в пространстве группирования.
Скорость электрона на выходе из зазора резонатора определяется уравнением скоростной модуляции:
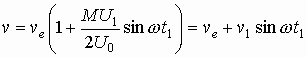 (3.25)
(3.25)
где v1=M1U1ve/2U0; t1 — момент прохождения электрона через центр зазора в “прямом” направлении; U1 — амплитуда синусоидального напряжения между сетками резонатора.
Электрон со скоростью и попадает в пространство между резонатором и отражателем, где на него действует электрическое поле напряженностью Е. Считая поле между сеткой резонатора и отражателем однородным, находим напряженность электрического поля
E=(U0-Uотр)/S (3.26)
где U0 — постоянное напряжение между катодом и резонатором; Uотр<0 — напряжение на отражателе; s — расстояние между второй сеткой резонатора и отражателем.
Под действием поля напряженностью Е электрон двигается равнозамедленно до определенной точки z=z', в которой скорость его станет равной нулю и начнется движение в обратном направлении. Уравнение движения электрона для данного случая (электрон движется вдоль силовых линий электрического поля по оси z) можно записать
m(d2z/dt2) = -eE. (3.27)
Поместим начало координат z=0 в плоскости второй сетки. Интегрируя (3.27) и используя начальные условия: t=t1, dz/dt=v, получим
Z = 0.5(eE/m)(t – t1)2+v(t – t1), (3.28)
где v — скорость электрона в плоскости второй сетки, которая определяется (3.25). Время пролета электрона в пространстве группирования от второй сетки до точки поворота и обратно можно найти из условий z=0, t=t2. Через t2, обозначим время возвращения электрона в плоскость рассматриваемой сетки. Применяя эти условия к (3.28), получаем два решения:
t2 – t1 = 0; (eE/2m)(t2 – t1) – v = 0
первое решение тривиально, а второе позволяет определить время пролета электронов
τ = (t2 – t1) = 2mv/eE (3.29)
Подставив в (3.29) значение Е из (3.26), получаем
τ = (2m/e)[sv/(U0-Uотр)] (3.30)
Так как скорость невозмущенного электрона, находящегося в центре сгустка, не изменяется при первом прохождении высокочастотного зазора, то вместо v можно в (3.30) подставить ve. Подставляя затем (3.30) в (3.24), получаем
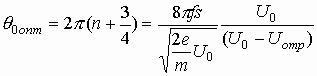 (3.31)
(3.31)
где f — частота генерируемых колебаний.
Формула (3.31) позволяет при данных f, s и U0 определить ряд значений Uотр, необходимых для получения оптимальных углов пролета, соответствующих различным номерам n. С ростом номера n необходимое абсолютное значение напряжения |Uотр| уменьшается. Этот вывод очевиден, так как, чем больше номер n, т.е. больше угол пролета θ0, тем слабее должно быть тормозят поле (3.26), создаваемое отражателем. На рис. 3.16, а показаны пространственно-временные диаграммы, соответствующие оптимальным углам пролета при n=3, 2 и 1.
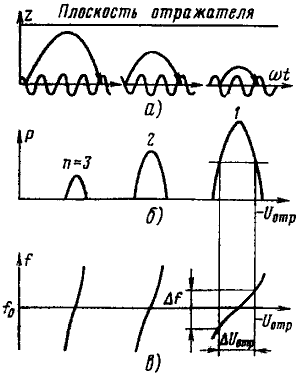 Рис. 3.16
Рис. 3.16
Передача энергии от электронного сгустка СВЧ полю резонатора должна ухудшаться, если угол пролета отличается от оптимального, и полностью прекратится, если невозмущенный электрон, являющийся центром сгустка, возвращается в резонатор в моменты нулевого поля, т. е. при θ0 опт —π/2 θ или θ0 опт+π/2. Β этих случаях половина электронов попадает в ускоряющее поле резонатора, а вторая половина — в тормозящее: в среднем, сколько энергии отбирается от поля, столько же передается ему потоком электронов.
Таким образом, вблизи каждого оптимального угла пролета имеется область значений ±π/2, в пределах которой возможна передача энергии от электронного тока СВЧ полю и генерация колебаний. Следовательно имеется ряд областей значений Uотр, соответствующих различным номерам n, в которых в возможна генерация колебаний. Поэтому зависимость мощности колебаний напряжения отражателя имеет зонный характер (рис. 3.16б), а номер n называется номером зоны генерации.
Параметры и характеристики. На рис. 3.16, б представлена зависимой генерируемой клистроном мощности от напряжения на отражателе. В центре каждой зоны мощность колебаний максимальна и соответствует прохождению сгустка электронов в момент максимального тормозящего поля между сутками резонатора. Из (3.31) можно получить выражение для напряжения отражателя, при котором выходная мощность максимальна (центры зон).
Вычислим разность фаз вылета электрона и его возвращения в центр зазора, воспользовавшись (3.29) и (3.26):
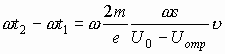 (3.32)
(3.32)
Подставляя в (3.32) значение v из (3.25), имеем
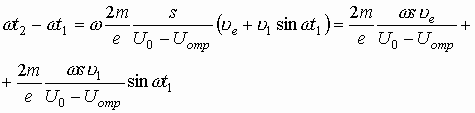 (3.33)
(3.33)
Первый член в правой части (3.33) — невозмущенный угод пролета θ0, соответствующий движению от второй сетки к отражателю и обратно. Тогда (3.33) можно представить в виде
![]() (3.34)
(3.34)
где параметр группирования с учетом v1 из (3.25)
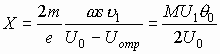 (3.35)
(3.35)
Соотношение (3.34) аналогично по форме (3.7), полученному для двухрезонаторного клистрона, но отличается от него знаком перед последним слагаемым.
Отличие в знаке объясняется тем, что группирование идет около невозмущенного электрона, смещенного на полпериода по сравнению с пролетным клистроном (см. рис. 3.3 и 3.15). Конвекционный ток отражательного клистрона рассчитывается, как в пролетном клистроне, и изменяется во времени так же, как показано на рис. 3.5. Спектр конвекционного тока аналогичен (3.14):
![]() (3.36)
(3.36)
Как и в теории пролетного клистрона, получаем выражение для амплитуды первой гармоники конвекционного тока
![]() (3.37)
(3.37)
амплитуда первой гармоники наведенного тока в выходном резонаторе
![]() (3.38)
(3.38)
где M1 — коэффициент электронного взаимодействия.
При оптимальном угле пролета (в центре зоны) максимальная мощность электронного взаимодействия
![]() (3.39)
(3.39)
Подставляя в (3.39) амплитуду (3.38), получим
![]() (3.40)
(3.40)
Используя (3.6), выразим U1 через параметр группирования:
![]() (3.41)
(3.41)
Подставляя в (3.40) величину (3.41) и принимая θ0= θ0 опт=2π(n+3/4), получим
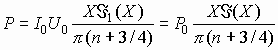 (3.42)
(3.42)
Соответственно в центре зоны максимальный электронный КПД
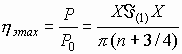 (3.43)
(3.43)
Однако (3.42) и (3.43) дают большую ошибку при малых номеpax зон (n=0; 1), так как принятое в теории предположение U1<<U0 в этом случае не выполняется.
Электронный КПД отражательных клистронов в различны зонах оказывается неодинаковым и уменьшается с ростом номера зоны n. Максимальный электронный КПД отражательны клистронов оказывается ниже, чем у пролетных клистронов. Реально достижимые значения полного коэффициента полезного действия отражательного клистрона не превышают нескольких процентов.
Одно из замечательных свойств отражательного клистрона, определивших широкое использование его в различных радиотехнических устройствах, — электронная перестройка частоты — явление изменения частоты генерируемых колебаний при изменения напряжения на отражателе или ускоряющего напряжения (рис 3.16 б).
Изменение напряжения на отражателе приводит к изменению угла пролета невозмущенного электрона и фазового сдвига между первой гармоникой конвекционного тока и напряжением на резонаторе, т.е. к изменению сдвига фазы между гармоникой, наведенного тока и напряжением. Последнее эквивалентно изменению активной и реактивной проводимостей, вносимых в резонатор электронным потоком.
Выше был рассмотрен случай, когда угол пролета был равен θ0=2πn+3/4). При этом первая гармоника наведенного тока совпадает по фазе с напряжением между сетками резонатора, реактивная составляющая электронной проводимости равна нулю и частота совпадает с собственной частотой резонатора. Таким образом в центре зон частота равна собственной частоте резонатора ω0
Очевидно, что изменение частоты ∆ω от значения в центре зоны ω0 определяется фазо-частотной характеристикой резонатора, который должен скомпенсировать фазовый сдвиг, вносимый электронным потоком; ФЧХ определяется нагруженной добротностью Qн. Чем больше Qн, тем при меньшем изменении ∆ω можно получить то же значение реактивной проводимости, вызванное изменением напряжения на отражателе. Расчет показывает, что зависимость ∆ω от добротности и изменения напряжения отражателя, а также от значения напряжения в центре зоны Uотр для различных номеров зоны n представляется формулой,
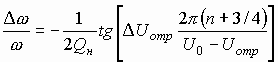 (3.44)
(3.44)
На практике используется только электронная перестройка частоты путем изменения напряжения на отражателе. Это объясняется тем, что ток в цепи отражателя равен нулю, и поэтому частотой клистрона можно управлять без затраты мощности.
Электронная перестройка характеризуется крутизной — отношением изменения частоты генерируемых колебаний к изменению напряжения на отражателе.
Из рис. 3.16 видно, что с увеличением номера зоны снижается максимальная электронная мощность в ней и возрастает крутизна кривой электронной перестройки. Электронная перестройка практически безынерционна, скорость изменения частоты ограничивается лишь переходными процессами в резонаторе и электронном потоке.
Важным параметром электронной перестройки является ее диапазон ∆f (т. е. область частот), в пределах которого электронная мощность изменяется на 3 дБ относительно максимального значения мощности в данной зоне (рис. З.16 б, в). Диапазон электронной перестройки отражательных клистронов обычно составляет около 0,5% средней частоты. Увеличить линейный участок характеристики электронной перестройки частоты около центра зоны можно путем введения дополнительного резонатора, связанного с основным.
Применение отражательных клистронов. Отражательные клистроны широко используются в различной аппаратуре в качестве маломощных генераторов. Основные преимущества их в сравнении с другими маломощными генераторами СВЧ заключаются в конструктивной простоте и наличии электронной перестройки частоты. Отражательные клистроны имеют также высокую надежность и не требуют применения фокусирующих систем.
Вследствие низкого КПД отражательные клистроны не используются для получения больших мощностей. Они применяются в качестве гетеродинов СВЧ приемников, в измерительной аппаратуре, в маломощных передатчиках, в радиорелейной, радионавигационной и телевизионной аппаратуре. В настоящее время отражательные клистроны вытесняются полупроводниковыми генераторами СВЧ, Для генераторов радиорелейных станций они имеют повышенную выходную мощность (1—10 Вт). Для диапазона волн от 60 до 4 см изготавливаются стеклянные клистроны с внешним резонатором с широким диапазоном перестройки частоты.
Для сантиметровых и миллиметровых волн выпускаются металлические клистроны с внутренним резонатором, диапазон перестройки которых не превышает ±10%. Некоторые металлические клистроны имеют устройство для быстрой механической перестройки частоты в виде кулачкового механизма, меняющего конфигурацию стенок резонатора. Внешний вид клистрона К-108 с внутренним резонатором и волноводным выводом энергии показан на рис. 3.17. Используется в передвижных маломощных телевизионных передатчиках.
Отражательные клистроны часто используются в режимах амплитудной или частотной модуляции. Наиболее распространенным и удобным способом модуляции в отражательных клистронах является изменение напряжения на отражателе, поскольку его цепь практически не потребляет мощности. При этом ускоряющее напряжение и ток пучка могут оставаться неизменными. Переменное модулирующее напряжение подается да отражатель клистрона. Получение только ЧМ при изменении напряжения на отражателе, как видно из рис. 3.16 — затруднительно. При изменении напряжения на отражателе наряду с частотой изменяется также и выходная мощность. Только при весьма неглубокой ЧМ в середине зоны, вблизи максимального значения выходной мощности, изменения амплитуд колебаний оказываются сравнительно небольшими. В противном случае необходим амплитудный ограничитель.

Рис. 3.17
Указанных трудностей можно избежать, если для управления амплитудой и частой колебаний одновременно использовать изменение напряжений на отражателе и резонаторе. Так как частота генерируемых, колебаний зависит не только от напряжения на отражателе Uотр, но и от ускоряющего напряжения на резонаторе U0, то представляется возможным при AM путем одновременного изменения по соответствующему закону напряжений резонатора и отражателя существенно снизить или даже практически устранить нежелательные изменения частоты. Однако это требует применения достаточно сложных схем.
Для повышения стабильности частоты отражательных клистронов используются стабилизирующие резонаторы с очень высокой добротностью, в том числе сверхпроводящие.
В настоящее время клистронов малой мощности коснулась тенденция миниатюризации. Реализация этого направления связана не только с решение конструктивно-технологических задач, но и с освоением новых режимов работы приборов. Миниатюризация — это не только уменьшение размеров прибора, но и снижение питающих напряжений, что позволяет уменьшить габариты и массу источников питания. Как показали исследования, для каждого значения подводимой к клистрону мощности питания Р0 существует низковольтная граница питающего напряжения U0 гр, за которой принципиально меняется характер процессов в электронных потоках клистронов. Величина U0 гр определяется формулой
U0 гр = 65,9 P02/5.
Физически это объясняется тем, что при заданной мощности снижение напряжения надо компенсировать увеличением тока, которое приведет к росту плотности пространственного заряда. При этом если не принять специальных мер, возникают специфические явления, связанные с недопустимо большим провисанием статического потенциала в потоке, нарушающим нормальную работу приборов.
Исследование природы этих ограничений позволило ученым разработать более совершенные конструкции миниатюрных пролетных и отражательных клистронов (последние получили название минитронов). Эти приборы имеют более высокие электрические параметры, чем их неминиатюрные аналоги, отличаются существенно меньшими габаритами и массой (единицы кубических сантиметров и грамм) и работают при существенно более низких напряжениях питания (десятки вольт при уровне выходной мощности в десятки милливатт).
Контрольные вопросы.
- Конструкция и принцип действия двухрезонаторного пролетного клистрона.
- Скоростная модуляция потока и ее превращения в модуляцию потока по плотности.
- Многорезонаторные клистроны – усилители, принцип действия, основные показатели и характеристики.
- Объяснить устройство и работу отражательного клистрона.
- Объяснить группирование электронов в сгустки при работе клистрона в различных зонах.
- Что такое электронная проводимость, и какую роль играет ее активная и реактивная составляющие?
4. Лампы бегущей волны типа О (ЛБВО)
4.1. Принцип работы лампы бегущей волны
В клистроне электроны отдают СВЧ полю часть кинетической энергии в течение короткого промежутка времени, поэтому для увеличения мощности взаимодействия в пролетных клистронах необходимо увеличивать амплитуду высокочастотного электрического поля в зазоре резонатора. Для этого следует увеличить добротность резонаторов, что сужает рабочую полосу частот. Узкополосность является одним из основных недостатков усилительных клистронов.
Для создания широкополосных приборов необходимо использовать принцип непрерывного длительного взаимодействия электронного потока с полем бегущей электромагнитной волны в нерезонансной колебательной системе. В приборах с длительным взаимодействием, так же как и в клистронах, используется модуляция скорости электронов и плотности электронного потока. При сравнительно слабом входном сигнале в результате длительного взаимодействия электронов с полем бегущей волны получается необходимое группирование электронов. Очевидно, что обмен энергией между электронами и полем происходит в результате взаимодействия электронов с составляющей напряженности электрического поля, совпадающей по направлению со скоростью электронов.
Для эффективного взаимодействия электронов с бегущей волной нужно, чтобы скорость электрона ve была приближенно равна фазовой скорости электромагнитной волны vф в направлении движения электронов. Это называется условием фазового синхронизма и записывается следующим образом:
ve – vф ≈ 0 (4.1)
Так как скорость электронов всегда меньше скорости света & свободном пространстве, то для выполнения (4.1) необходимо уменьшать фазовую скорость волны, взаимодействующей с электронами. Для этого используются специальные устройства, которые называются замедляющими системами.
Наглядное представление о группировании электронов дает пространственно-временная диаграмма, представленная на рис. 4.1. В системе координат, движущейся с фазовой скоростью волны, сплошными линиями показано смещение электронов ∆z относительно волны, а пунктирными — движение электронов в этой же системе координат при отсутствии поля волны. Процесс группирования зависит от соотношения скорости электронов ve скорости электромагнитной волны vф.
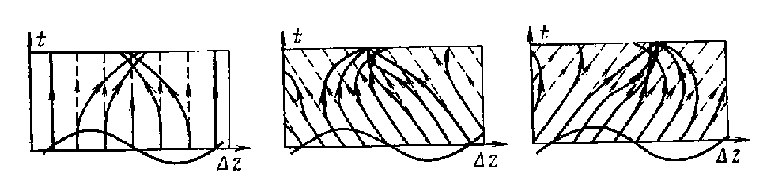 Рис. 4.1
Рис. 4.1
Если vе=vф, то электроны группируются в области нулевого значения высокочастотного поля (рис. 4.1 а) и электронный поток не обменивается энергией с бегущей волной. Если Vе<Vф, то электроны отстают от волны и группируются в области ускоряющего высокочастотного поля (рис. 4.1 б), которое сообщает электронам дополнительную скорость. В результате входной сигнал не усиливается, а ослабляется. Если Vе>Vф, то электроны, находящиеся в ускоряющем поле, приобретают ускорение и перемещаются в область тормозящего поля (рис. 4.1 в), где их движение, замедляется. Следовательно, электроны будут сосредоточены в тормозящем поле и передадут частично свою кинетическую энергию бегущей волне. Амплитуда электромагнитной волны по мере распространения вдоль замедляющей системы будет возрастать. Поэтому необходимым условием усиления ЛБВ является такое соотношение между скоростями Vе и Vф, при котором скорость электронов Vе немного превышает скорость электромагнитной волны.
Так как скорость электронов в процессе взаимодействия с полем будет уменьшаться, то по мере движения вдоль замедляющей системы сгустки электронов будут смещаться относительно бегущей волны. Необходимо такое различие в скоростях, чтобы за время движения сгустка вдоль всей длины замедляющей системы он не вышел из области тормозящего поля.
Принцип действия ламп бегущей волны (ЛБВ) основан на рассмотренном выше механизме длительного взаимодействия электронного потока с полем бегущей электромагнитной волны. На рис. 4.2 схематично представлено устройство ЛБВ. Электронная пушка формирует электронный пучок с определенным сечением и интенсивностью. Скорость электронов определяется ускоряющим напряжением. С помощью фокусирующей системы 3, создающей продольное магнитное поле, обеспечивается необходимое поперечное сечение пучка на всем пути вдоль замедляющей системы. В ЛБВ электронная пушка, спиральная замедляющая система 2 и коллектор 5 размещаются в металлостеклянном или металлокерамическом баллоне 7, а фокусирующий соленоид 3 располагается снаружи. Спираль крепится между диэлектрическими стержнями, которые должны обладать малыми потерями на СВЧ и хорошей теплопроводностью. Последнее требование важно для ламп средней и большой выходной мощности, когда спираль нагревается из-за оседания электронов и нужно отводить это тепло, чтобы не было прогорания спирали.
На входе и выходе замедляющей системы есть специальные устройства 4 для согласования ее с линиями передачи. Последние могут быть либо волноводными, либо коаксиальными. На вход поступает СВЧ сигнал, который усиливается в приборе и с выхода передается в нагрузку.
Трудно получить хорошее согласование во всей полосе усиления лампы. Поэтому есть опасность возникновения внутренней обратной связи из-за отражения электромагнитной волны на концах замедляющей системы, при этом ЛБВ может перестать выполнять свои функции усилителя. Для устранения самовозбуждения вводится поглотитель 6, который может быть выполнен в виде стержня из поглощающей керамики или в виде поглощающих пленок.
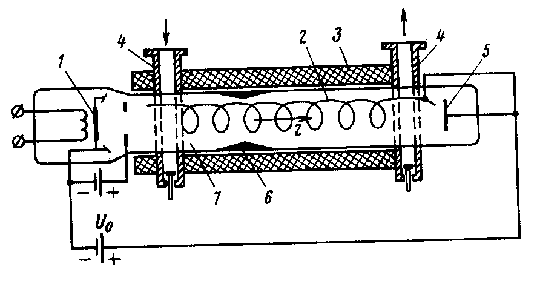
Рис. 4.2
4.2. Замедляющие системы
Наибольшее распространение в технике СВЧ получили замедляющие системы, представляющие собой линии передачи с периодически повторяющимися неоднородностями. Некоторые из них представлены на рис. 4.3, где 1 — спираль, 2 — гребенка, 3 —встречные штыри, 4 — сдвоенный меандр на диэлектрической подложке, 5 — диафрагмированный волновод, 6 —диафрагмированный волновод с индуктивными щелями связи, 7 — “лист клевера”, 8 — меандр на диэлектрической подложке.
Широко используется замедляющая система в виде цилиндрической спирали. Эта замедляющая система была использована Р. Компфнером в 1944 г. в первой ЛБВ, и сейчас большинство серийно выпускаемых ЛБВ тоже использует спиральную замедляющую систему, что объясняется многими ее достоинствами. Ни, одна из известных замедляющих систем не может конкурировать, со спиралью в отношении широкополосности. При упрощенном рассмотрении процессов в такой системе можно предполагать, что волна Т распространяется со скоростью света с вдоль спирального проводника. Пусть D будет средний диаметр спирали, a L – ее шаг. Тогда время, за которое волна обегает один виток,
![]()
![]()
![]()
Если шаг спирали много меньше диаметра, т. е. L<<πD, имеен t<<πD/c. Волна за то же время проходит вдоль оси спирали путь, равный L. Следовательно, фазовая скорость волны ve вдоль оси спирали равна L/t или vф=cL/πD.
Обычно замедляющую систему характеризуют коэффициентом замедления Кзам, равным отношению скорости света к фазовой скорости замедленной электромагнитной волны.
Рис. 4.3
Тогда Kзам=c/vф=πD/L (4.2)
Коэффициент замедления тем больше, чем больше отношение длины витка к шагу спирали. Изменяя диаметр спирали D и ее шаг L, можно в широких пределах изменять коэффициент замедления.
Более точный анализ распространения электромагнитных волн вдоль спирали показывает, что спираль обладает дисперсией, т. е. фазовая скорость волны в спирали зависит от частоты. Но на достаточно высоких частотах (4.2) дает хорошее приближение.
Рассмотрим некоторые общие закономерности распространения электромагнитных волн в замедляющих системах. Замедляющие системы представляют собой периодические структуры, имеющие свойства полосовых фильтров с бесконечным числом полос пропускания. В приборах используется чаще всего полоса, пропускающая самые низкие частоты, она называется основной. Остальные полосы называются высшими.
Поле в периодической структуре удовлетворяет теореме Флоке, которая утверждает, что среди решений уравнений Максвелла, удовлетворяющих граничным условиям, всегда найдется такое решение, при котором поля в соседних ячейках отличаются лишь постоянным множителем p=e-r, т. е. E(z+L)=e-r Е(г). В полосе пропускания для систем без потерь величина Г=iψ – мнимая. Это означает, что поле в соседних ячейках отличается лишь сдвигом по фазе на угол ψ. Введем обозначение ψ=β0L (β0—постоянная распространения волны) и умножив обе части равенства на ехрiβo(L+z), при этом заметим, что функция E0(z)=E(z)ехрiβoz=E(z)ехрiβo(z+L) — периодическая, а ее период совпадает с периодом структуры L. Отсюда следует, что поле в системе E(z) можно представить в виде произведения двух периодических функций: E0(z) и ехрiβoz. Учитывая и временной множитель ехрiωt, можно записать
E(z,t)=E0(z)ei(ωt-βoz) (4.3)
Функция E0(z) — периодическая, L — ее период. Разложение E0(z) в ряд Фурье дает
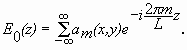 (4.4)
(4.4)
где
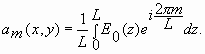
Подставляя (4.4) в (4.3), получим
![]() (4.5)
(4.5)
Распределение поля в системе представлено в виде суммы бесконечного числа бегущих волн с амплитудами am(x,у) и постоянными распространения
![]() (4.6)
(4.6)
Эти волны называются пространственными гармониками. Их совокупность удовлетворяет периодическим граничным условиям. Решение в виде одной пространственной гармоники не может удовлетворить граничным условиям. Все гармоники изменяются с одной и той же частотой. Каждой пространственной гармонике соответствует своя фазовая скорость, которая определяется соотношением
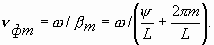 (4.7)
(4.7)
Групповая скорость всех пространственных гармоник одинакова:
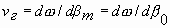 (4.8)
(4.8)
Зависимость фазовой скорости (или коэффициента замедления) от частоты в свободном пространстве называется дисперсией замедляющей системы, а графики этих зависимостей — дисперсионными характеристиками или кривыми дисперсии. Каждой пространственной гармонике соответствует определенная ветвь дисперсионной характеристики.
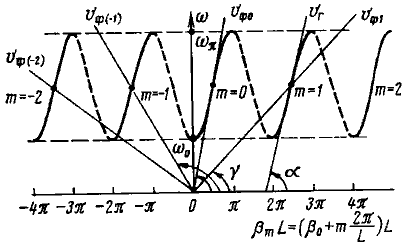
Рис. 4.4
Волна (или пространств венная гармоника), у которой направления групповой и фазовой скоростей одинаковые, называется прямой волной, волна с противоположными направлениями скоростей — обратной волной.
В зависимости от знака производной d|vфm|/dω дисперсия может быть нормальной (d|vфm|/dω<0) и аномальной (d|vфm|/dω >0). При увеличении частоты нормальная дисперсия характеризуется уменьшением абсолютного значения фазовой скорости, а аномальная — ростом. Для всех обратных гармоник дисперсия аномальная, прямые гармоники могут иметь как нормальную, так и аномальную дисперсию.
На рис 4.4. показана дисперсионная характеристика замедляющей системы. По оси абсцисс отложен фазовый сдвиг на один период замедляющей системы βmL, определяемый (4.6), а по оси ординат—частотаω. Сплошные кривые относятся к гармоникам т=0, ±1, ±2. Нулевая гармоника (m=0) соответствует изменению угла от 0 до π. Эти пределы в соответствии с теорией фильтров определяют полосу пропускания, заключенную между ω0 и ωπ. Сдвиг фазы для гармоники m=+1 по определению (4.6) на 2π больше, чем при т=0, поэтому кривая для т=+1 существует в пределах (2![]() 3)π.Соответственно смещаются на 2π вправо кривые при каждом увеличении на единицу номера т. Переход от т=0 к т=-1 эквивалентен смещению кривой в область фазы от -π до -2π и т. д. Полоса пропускания для всех пространственных гармоник одинакова и равна полосе пропускания замедляющей системы.
3)π.Соответственно смещаются на 2π вправо кривые при каждом увеличении на единицу номера т. Переход от т=0 к т=-1 эквивалентен смещению кривой в область фазы от -π до -2π и т. д. Полоса пропускания для всех пространственных гармоник одинакова и равна полосе пропускания замедляющей системы.
Фазовая скорость гармоники с учетом (4.7) пропорциональна тангенсу угла наклона у прямой, проведенной через начало координат и точку дисперсионной кривой для выбранной частоты <0. Групповая скорость гармоники пропорциональна производной в данной точке, т. е. tg a. Очевидно, что на границах полосы пропускания групповая скорость гармоник равна нулю (экстремальные точки кривых). Групповая скорость всех пространственных гармоник при данной частоте ω одинакова и положительна. Для варианта замедляющей системы, дисперсионная характеристика которой приведена на рис. 4.4, наибольшая фазовая скорость у нулевой гармоники. С увеличением положительного номера т фазовая скорость уменьшается, фазовые скорости гармоник m= -1, -2 отрицательны (противоположны направлению групповой скорости) и также уменьшаются с ростом номера. В рассматриваемом случае гармоники m=0, +1, +2 — прямые, а m= -1, -2 — обратные.
Используя дисперсионные кривые, можно выяснить зависимость фазовой скорости любой пространственной гармоники от частоты. В нашем примере прямая нулевая гармоника имеет нормальную дисперсию (фазовая скорость уменьшается с ростом частоты). Обратные гармоники (т= -1, -2) обладают аномальной дисперсией. Легко убедиться, что для прямой гармоники т=+2 вблизи границ пропускания дисперсия нормальная, а в остальной области аномальная.
Важной характеристикой замедляющей системы является сопротивление связи, которое характеризует эффективность взаимодействия электронного потока с полем в замедляющей системе. По определению сопротивление связи
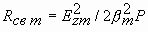 (4.9)
(4.9)
Чем больше продольная составляющая напряженности электрического поля Еzm в месте прохождения электронного пучка при данном потоке мощности Р в системе, тем больше сопротивление связи.
Если выразить поток мощности через запасенную энергию W на единицу длины системы и групповую скорость (P=vгW), то сопротивление связи
![]() (4.10)
(4.10)
Так как групповая скорость входит в выражение для сопротивления связи, то Rсв тем больше, чем меньше крутизна tg a дисперсионной характеристики (см. рис. 4.4).
Изменяя скорость электронов ve регулировкой ускоряющего напряжения, можно выполнить условия синхронизма для любой пространственной гармоники. Так как фазовая скорость нулевое пространственной гармоники наибольшая, то для взаимодействия с ней необходима наибольшая скорость электронов, что требует высокого ускоряющего напряжения. Для взаимодействия электронного потока с высшими гармониками замедляющей систем скорость электронов должна быть меньше и соответственно меньше будут ускоряющие напряжения. Однако взаимодействие с высшими пространственными гармониками для систем 1, 2, 6 рис. 4.3 получается неэффективным, поскольку они имеют малое сопротивление связи. Поэтому в приборах СВЧ используются в основном нулевая и плюс первая или минус первая гармоника. Прямые пространственные гармоники используются в ЛБВ, а обратные — в ЛОВ. Дисперсионная характеристика замедляющей системы определяют ширину полосы частот усилителя и диапазон электронной перестройки генератора.
Строгий метод расчета замедляющих систем основывается на решении уравнений Максвелла с учетом конкретных граничных условий. Однако сложность конфигурации большинства замедляющих систем затрудняет решение этой задачи. Часто применяются различные приближенные методы, среди которых широко распространен метод эквивалентных схем. Замедляющая система представляется эквивалентной схемой в виде цепочки ячеек фильтра с сосредоточенными постоянными. Этот метод позволяет оценить ширину полосы пропускания, а также качественно определить влияние отдельных элементов замедляющей системы на характеристики.
4.3. Элементы линейной теории ЛБВ
Обычно ЛБВ используются для усиления слабого сигнала. В этом случае приближенный анализ процесса взаимодействия электронного потока с полем бегущей волны возможен на основе линейной теории ЛБВ. При этом предполагается, что все переменные составляющие величин, характеризующих электронный ток, много меньше их постоянных составляющих.
Задачу взаимодействия электронного потока с полем бегущей волны рассматривают в три этапа. Сначала анализируется вопрос о возбуждении сгруппированным электронным потоком волн в замедляющей системе, которая заменена эквивалентной длинной линией с распределенными постоянными. Затем рассматривается процесс группирования электронов под действием бегуну волны в замедляющей системе. Полученные на предыдущих этапах уравнения решаются совместно, в результате чего находит так называемое дисперсионное уравнение ЛБВ [З]. Опуская математические выкладки, запишем это уравнение
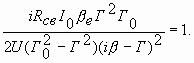 (4.11)
(4.11)
Г0 — постоянная распространения волн в замедляющей системе без электронного потока (холодная система); Г — постоянная распространения волн в замедляющей системе с электронным потоком (горячая система), βе=ω/ve.
Выражение (4.11) является уравнением четвертой степени относительно Г. Его решение определяет постоянные распространения для четырех волн в рассматриваемой системе. Из этих волн интерес представляют те, которые распространяются в направлении электронного пучка и имеют скорость, близкую к скорости электронов.
Предположим, что скорость электронов сделана равной скорости волны в линии без электронного потока, т. е. в (4.11)
Г0=iβe. (4.12)
Рассмотрим волны, скорость, которых близка к скорости электронов. В этом случае можно считать, что постоянная распространения Г отличается от βе на небольшую величину ξ. Тогда
Г=Г0 - ξ. (4.13)
Подставив (4.12) и (4.13) в (4.11), получаем
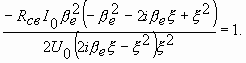 (4.14)
(4.14)
Если ξ<<βe, то в числителе можно пренебречь членами, содержащими βeξ и ξ2 по сравнению с β2e, а в знаменателе по сравнению с ξ2. В результате получаем
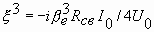 (4.15)
(4.15)
Обозначим
![]() (4.16)
(4.16)
и введем новую переменную ![]() . Тогда (4.15) примет вид
. Тогда (4.15) примет вид
![]() (4.17)
(4.17)
Это уравнение имеет три корня, соответствующие трем волнам, распространяющимся в направлении движения электронного потока и имеющим одинаковую структуру поля, но обладающим различными постоянными распространения. Корни уравнения:
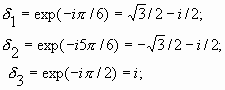
Четвертая волна не учитывается в (4.17), поскольку сделанные выше предположения справедливы только для первых трех волн, имеющих скорость, близкую к скорости электронов. Четвертая волна имеет постоянную распространения Г= -iβe(1 – C3/4).
Так как обычно C=0,01—0,1, то, следовательно, С3 очень мало. Таким образом, постоянная распространения четвертой волны в отсутствие электронов и при их наличии практически одинакова. Четвертая волна распространяется в обратном направлении (от коллектора к катоду), и ее постоянная распространения равна постоянной распространения в замедляющей системе без учета влияния электронного потока.
Решение (4.11) получено в предположении (4.12). Такое допущение не учитывает дисперсии замедляющей системы. Более строгий анализ процессов взаимодействия электронов с полем бегущей волны позволяет определить допустимое различие скоростей электронов и волны, при котором еще возможно усиление лампы. Это различие приближенно можно оценить по формуле [3,5]
|vф – vе| ≈ vеC.
Таким образом рабочая полоса частот ЛБВ тем шире, чем больше параметр С и чем меньше зависит от частоты фазовая скорость электромагнитной волны в замедляющей системе (чем слабее дисперсия).
Три волны изменяются с расстоянием по закону
![]() (4.18)
(4.18)
Подставляя полученные три значения δ в (4.18), можно убедится, что для первых двух волн постоянная распространения буде комплексной величиной. Это значит, что амплитуды данных волн будут изменяться вдоль замедляющей системы. Первая волна является нарастающей, фазовая скорость ее немного ниже скорости электронов. Амплитуда второй волны уменьшается, и она распространяется также несколько медленнее электронов. Третья волна — незатухающая, и распространяется быстрее электронов. Таким образом, наибольший интерес для усиления волн в ЛБВ представляет первая волна, амплитуда которой и, cлeдовательно, переносимая ею мощность экспоненциально возрастают вдоль замедляющей системы.
4.4. Параметры и характеристики ЛБВ
Коэффициент усиления. Можно доказать, что энергия на входе лампы равномерно распределяется между тремя волнами. Следовательно, амплитуда каждой волны равна Е(z=o)/3. Тогда напряженность электрического поля в конце замедляющей системы для нарастающей волны
![]()
Постоянная распространения в системе без электронного потока для пространственной гармоники с длиной волны Λ: Г0=2π/Λ,
поэтому с учетом (4.12)
![]()
где N=l/Λ — электрическая длина замедляющей системы.Используя величину βel ,получим
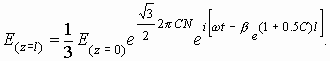 (4.19)
(4.19)
Зная амплитуды волн в начале и в конце замедляющей системы, можно определить коэффициент усиления ЛБВ по напряжению в децибелах
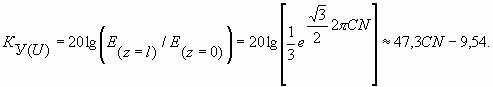 (4.20)
(4.20)
Значение K=9,54 дБ — это начальные потери, обусловленные тем, что амплитуда входного сигнала ЛБВ распределяется поровну между тремя волнами, т. e. напряженность поля нарастающей волны на входе ЛБВ в 3 раза меньше напряженности входного сигнала.
Формула (4.20) широко используется при расчетах ЛБВ для линейного режима (малого сигнала). Параметр С называется параметром усиления. Согласно (4.16) параметр С увеличивается при увеличении сопротивления связи замедляющей системы. Коэффициент усиления ЛБВ прямо пропорционален параметру усиления и электрической длине лампы, определяемой N.
Существуют пределы, ограничивающие рост коэффициента усиления. При большой длине ЛБВ линейная теория, из которой получена формула (4.20), оказывается несправедливой на конечном участке ЛБВ. Кроме того, существует опасность самовозбуждения вследствие возможного отражения сигнала от нагрузки. Для борьбы с самовозбуждением применяют поглотитель (элемент 6 на рис. 4.2), ослабляющий отраженную волну.
Реально достижимое значение коэффициента усиления ЛБВ обычно 25—40 дБ, т. e. несколько ниже, чем у многорезонаторных клистронов. В маломощных ЛБВ коэффициент усиления выше и может достигать 60 дБ.
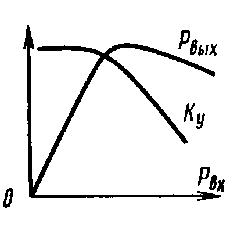 Рис. 4.5
Рис. 4.5
Амплитудная характеристика. Типичная зависимость выходной мощности и. коэффициента усиления от уровня входной мощности приведена на рис. 4.5. Начальный участок характеристик линеен. С увеличением входной мощности наступает насыщение, вызванное смещением сгустка в область нулевого поля волны вследствие торможения электронов при взаимодействии с волной. Коэффициент усиления ЛБВ имеет наибольшее значение Па линейном участке характеристики, а электронный КПД — в максимуме амплитудной характеристики. Поэтому при работе ЛБВ в качестве входного усилителя, когда важен высокий коэффициент усиления, используют линейный участок амплитудной характеристики. В мощных выходных усилителях передатчик ЛБВ работают в режиме максимального КПД.
Коэффициент полезного действия. Для определения максимального значения электронного КПД необходимо рассматривать работу ЛБВ в нелинейном режиме и учесть влияние пространств венного заряда. Кулоновские силы расталкивания, препятствуй группированию электронов, вызывают уменьшение коэффициента усиления и электронного КПД. Существует оптимальный режим при котором электронный КПД имеет максимальное значение ηэ max. При не очень больших параметрах усиления (С<0,1)
ηэ max=(2÷3)С. (4.21)
Параметр С определяет не только коэффициент усиления лампы (4.20), но и максимальный КПД. Следовательно, для увеличения КПД необходимо увеличивать С (4.16), т. е. повышать сопротивление связи замедляющей системы и увеличивать отношение I0/U0. Реальный КПД мощных ЛБВ меньше, чем у мощных многорезонаторных клистронов, и составляет примерно 25 – 30%.
Один из известных методов повышения КПД заключается, использовании замедляющих систем с переменным коэффициентом замедления (4.2) для сохранения синхронизма между скоростью электронов и фазовой скоростью электромагнитной волны. Дело в том, что электроны, отдавая энергию волне, постепенно замедляют свое движение и электронный сгусток смещается в область ускоряющей полуволны поля. Тем самым нарушается первоначальное условие синхронизма. Поэтому замедляющую систему конструируют так, чтобы было некоторое увеличение коэффициента замедления к выходному концу лампы. При спиральной замедляющей системе это достигается плавным уменьшением шага спирали. Такие ЛБВ называются изохронными.
Эффективен и широко распространен метод повышения КПД с помощью торможения электронов после замедляющей системы. При этом понижается потенциал коллектора по сравнению с потенциалом замедляющей системы. Пучок электронов после прохождения замедляющей системы поступает на коллектор, где рассеивается оставшаяся кинетическая энергия. Так как в ЛБВ весь ток пучка идет в цепи коллектора, потенциал которого обычно равен потенциалу замедляющей системы, то от источника питания коллектора потребляется мощность P0=I0U0. Если теперь потенциал замедляющей системы остался неизменным, а потенциал коллектора уменьшился, то выходная мощность ЛБВ останется прежней, а мощность, потребляемая от источника питания коллектора, снизится, что означает повышение КПД. Физически это объясняется тем, что электроны тормозятся в пространстве между замедляющей системой и коллектором и рассеивают на коллекторе меньшую кинетическую энергию. Торможение означает переход некоторой части кинетической энергии в энергию электростатического поля и возврат (рекуперация) энергии в источник питания.
Поскольку в пучке присутствуют электроны с различными энергиями, увеличение КПД достигается наиболее эффективно в секционированных коллекторах, в которых на секции подаются различные потенциалы. Степень допустимого понижения напряжения на коллекторе определяется распределением электронов по скоростям и ограничивается возможностью возникновения обратной связи за счет обратных электронов, летящих с коллектора, которые вызывают нагрев замедляющей системы.
Частотная характеристика ЛБВ — зависимость выходной мощности (или коэффициента усиления) от частоты при фиксированной входной мощности. Такая характеристика приведена на рис. 4.6. По ней можно определить ширину рабочей полосы частот ЛБВ, которая составляет от нескольких десятков до сотни процентов средней частоты диапазона. Широкополосность — особенно ценное свойство ЛБВ.
 Рис. 4.6
Рис. 4.6
Фазовые характеристики ЛБВ определяют зависимость разности фаз колебаний на входе и выходе от различных причин: частоты усиливаемых колебаний, изменения ускоряющего напряжения, тока пучка и т. д. Фазовые характеристики необходимы для оценки искажений широкополосных сигналов, усиливаемых ЛБВ.
Широкое применение ЛБВ в системах связи налагает определенные требования к характеристикам этих приборов. Это, прежде всего требование минимальных нелинейных искажений усиливаемых сигналов. В системах связи необходимо одновременно усиливать несколько сигналов с близкими частотами, поэтому в ЛБВ, как и в любом нелинейном элементе, возникают следующие искажения: изменение фазы сигнала на выходе в зависимости от уровня входного сигнала, появление в спектре выходного сигнала составляющих с частотами, кратными частотам усиливаемых сигналов, а также сигналов на суммарной частоте, появление комбинационных составляющих вида mf1±nf2. Степень зависимости фазы выходного сигнала от уровня входного сигнала называется коэффициентом преобразования амплитудной модуляции в фазовую и определяется в градусах на децибел.
При усилении многочастотного сигнала в ЛБВ наиболее существенны комбинационные составляющие, которые вызывают искажение полезной информации в соседних каналах связи. Теоретически и экспериментально показано, что формированием входного сигнала специальной формы можно существенно уменьшить уровень комбинационных составляющих третьего порядка на выходе. Оптимальным будет входной сигнал, содержащий составляющие удвоенной частоты усиливаемых сигналов.
Шумовые характеристики. Одной из важных характеристик маломощных ЛБВ является уровень собственных шумов, который определяет минимальный сигнал, подлежащий усилению.
Наиболее существенны собственные шумы электронного потока. Эмиссия с катода вызывает шумы в виде случайных изменений плотности конвекционного тока и скоростей электронов (дробовой эффект). Уровень шумов зависит от конструкции электронной пушки и режима ее работы. Шумы электронного потока, уменьшают, создавая определенные изменения потенциала между катодом и началом замедляющей системы, для чего применяют электронные пушки специальной многоанодной конструкции.
Другим источником шумов ЛБВ является шум, который возникает из-за оседания части электронов пучка на электродах пушки и на замедляющей системе. Влияние токораспределения на уровень шумов можно уменьшить хорошей фокусировкой пучка обеспечивающей практически прямолинейные траектории электронов. Возникновение собственных шумов в ЛБВ связано также тепловыми шумами замедляющей системы. Их мощность пропорциональна абсолютной температуре. Поэтому для снижения ypoвня шума наряду с улучшением шумовых свойств электронной пушки необходимо охлаждать ЛБВ, например, до температуря жидкого азота. Коэффициент шума современных промышленных ЛБВ 6—8 дБ на частоте 3 ГГц. Минимальный коэффициент шума, достижимый в настоящее время для ЛБВ, выше, чем у мазеров или полупроводниковых усилителей. Транзисторные усилители вытесняют малошумящие ЛБВ вплоть до частоты 12 ГГц с перспективой вытеснения до 18 ГГц. В этих условиях конкуренции идет совершенствование малошумящих ЛБВ с целью дальнейшего снижения массы при условии повышения выходной мощности и полосы пропускания на более высоких частотах. Разрабатывают малогабаритные малошумящие ЛБВ частотой до 40—60 ГГц, коэффициентом шума менее 18 дБ, усилением 35 дБ и выходной мощностью в режиме насыщения 20 мВт.
4.5. Особенности устройства и применения ЛБВ
Лампы бегущей волны в зависимости от уровня выходной мощности в режиме насыщения, как и другие электровакуумные приборы, подразделяются на следующие классы: маломощные (доли милливатта — 1 Вт), средней мощности (1—100 Вт), большой мощности (более 100 Вт) и сверхмощные (более 100 кBт). По режиму работы ЛБВ бывают импульсного и непрерывного действия. Для фокусировки электронного потока в первых разработанных ЛБВ применяли соленоиды, которые обычно громоздки и имеют большую массу. Существенно уменьшить габариты и массу ЛБВ удалось путем применения периодической фокусировки электронных потоков с использованием как электростатических, так и магнитных линз. Лампы с периодической магнитной фокусировкой называются пакетированными. В настоящее время для периодической магнитной фокусировки в ЛБВ (так же, как и для многорезонаторных клистронов) применяются магниты из самарий-кобальтового сплава, обладающего высокой коэрцитивной силой, которые имеют малые размеры.
В широкополосных ЛБВ малой и средней мощностей применяются спиральные замедляющие системы, характеризующиеся широкой полосой пропускания. Трудности теплоотвода от спирали сдерживают применение этой замедляющей системы для более мощных приборов. В настоящее время в ЛБВ со спиральной замедляющей системой достигнут уровень выходной мощности в непрерывном режиме примерно 1 кВт в диапазоне 5—10 ГГц. Однако работы по улучшению теплоотвода продолжаются, и в будущем возможно увеличение уровня выходной мощности.
В мощных ЛБВ в качестве замедляющих систем применяются цепочки связанных резонаторов (см. 6, 7 рис. 4.3). Полоса пропускания в таких ЛБВ меньше, но уровень мощности в непрерывном режиме достигает 15 кВт на частоте 10 ГГц.
Маломощные ЛБВ применяются для усиления входных сигналов в различных приемниках СВЧ, в частности во входных усилителях ретрансляционных станций радиорелейных линий связи. Как правило, такие ЛБВ являются малошумящими.
Средней мощности ЛБВ используются в качестве промежуточных усилителей, а также в качестве выходных усилителей мощности в маломощных передатчиках. На рис. 4.7 приведены ЛБВ средней мощности: 1 — УВ-7 вместе с фокусирующей системой в виде соленоида; 2 — УВ-229 без соленоида, 3 — ЛБВ с периодической фокусирующей системой из постоянных магнитов.
 Рис. 4.7
Рис. 4.7
Для ЛБВ средней мощности, используемых в системах связи, проводятся исследования по увеличению КПД и уменьшению нелинейных искажений. Эти две проблемы противоречивы. В радиорелейных линиях связи проблема повышения КПД не столь остра, как для ЛБВ, используемых в космосе, где для повышения КПД приходится мириться с увеличением нелинейных искажений. Коэффициент преобразования АМ/ФМ в космических ЛБВ обычно 4,5 — 6 град/дБ, в то время как для радиорелейных систем 1,5 — 4 град/дБ.
Приведем параметры ЛБВ средней мощности для систем космической связи ТН3525 (Франция), в которой успешно решены обе проблемы. Полоса пропускания этой ЛБВ 0,75 ГГц, а выходная мощность 20 Вт. Неравномерность частотной характеристики в полосе частот 125 МГц составляет ±0,2 дБ. Комбинационные составляющие третьего порядка при одинаковых уровнях двух несущих в режиме насыщения 11 дБ, коэффициент преобразования АМ/ФМ в односигнальном режиме не более 6 град/дБ, а в двухсигнальном — менее 4,5 град/дБ. Фазовый сдвиг при переходе от линейного режима к режиму насыщения 36°, а изменение времени задержки 0,5 нс. Общий уровень гармоник в режиме насыщения 15 дБ. В ЛБВ ТН3525 применена трехсекционная замедляющая система: первые две секции с постоянными, но различными для каждой секции шагом спирали, третья — с постоянно уменьшающимся шагом. Для повышения КПД применено понижение напряжения коллектора (рекуперация энергии). Общий КПД 40%.
Крупным техническим достижением в области космической связи стало так же создание ЛБВ средней мощности TL 12024 (ФРГ) с рекордным комплексом параметров: КПД 46% при выходной мощности 20 Вт, коэффициент преобразования 2,5 град/дБ, масса 0,65 кг, долговечность 500 тыс. ч.
Мощные и сверхмощные ЛБВ применяются в передатчиках радиолокационных станций различного назначения, в наземных станциях систем космической связи и т. д. Для мощных ЛБВ основное внимание уделяют получению максимально возможного КПД и выходной мощности.
Существующие ЛБВ перекрывают диапазон 0,5—100 ГГц. В последние годы (1978—1980 гг.) разработано много ЛБВ для систем космической связи на частотах выше 10 ГГц. Это ЛБВ средней мощности для спутников и мощные ЛБВ для наземных систем. В то же время промышленность почти прекратила выпуск малошумящих ЛБВ на частотах до 8 ГГц в связи с большими успехами в разработке малошумящих транзисторных усилителей и сократила производство некоторых мощных ЛБВ непрерывного действия в дециметровом диапазоне. Проводятся перспективные разработки ЛБВ для спутников в диапазонах частот 40 и 80 ГГц. Продолжаются работы по уменьшению габаритов и массы ЛБВ средней мощности. Созданы ЛБВ непрерывного действия с полосой частот в две октавы при выходной мощности 1 Вт и импульсные ЛБВ с полосой частот более октавы при выходной мощности 1 кВт и около октавы при 15 кВт.
Развитие систем радиопротиводействия вызвало необходимость разработок двухрежимных ЛБВ, которые в зависимости от режима питающих напряжений могут обеспечить попеременно импульсный или непрерывный режим работы. Применение таких ЛБВ приводит к существенному уменьшению массы и габаритов бортовой аппаратуры. Эти ЛБВ сложнее однорежимных, поэтому трудно получить хорошие КПД и высокое отношение импульсной мощности к непрерывной, которое составляет примерно 2,5 в диапазоне 6 — 15 ГГц и достигает 4 — 6 на частотах ниже 6 ГГц.
Одним из перспективных направлений развития ЛБВ является разработка ламп, замедляющая система которых и некоторые другие элементы выполняются путем напыления металлов на керамические платы. В будущем предполагается полный переход от объемных на планарные печатные элементы, которые изготавливаются технологическим процессом, аналогичным принятым в микроэлектронике для интегральных схем. Пленочная технология -обеспечивает высокую точность изготовления мелкоструктурных замедляющих систем с жесткими допусками, а также сложных замедляющих систем, которые трудно выполнить обычными методами.
Миниатюрные ЛБВ на печатных элементах характеризуются малыми размерами, низкой стоимостью и хорошей повторяемостью параметров от лампы к лампе. Это делает их перспективными для применения в фазированных антенных решетках, где вопросы стоимости и идентичности параметров ламп выступают на первое место. Параметры зарубежных приборов лежат в пределах: диапазон частот 3 — 6 ГГц, выходная мощность в непрерывном режиме 20 — 200 Вт, в импульсном — 200—2000 Вт, усиление 13 — 20 дБ, КПД 20 — 30%. Разрабатываются ЛБВ как для непрерывного, так и для импульсного режимов работы.
4.6. Лампа обратной волны
Устройство лампы обратной волны (ЛОВ) показано схематически на рис. 4.8, где 1 —электронная пушка, 2 —вывод энергии, 3 —замедляющая система, 4 —поглотитель, 5 —коллектор, 6 —фокусирующая система. В ней используется магнитная фокусировка электронного потока. В отличие от ЛБВ, электронный поток взаимодействует с одной из обратных пространственных гармоник бегущей волны, которая, как известно из § 4.2, характеризуется тем, что ее фазовая и групповая скорости имеют противоположные направления.
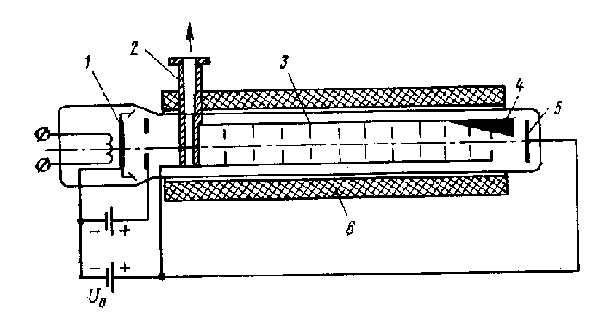 Рис. 4.8
Рис. 4.8
Так как сопротивление связи пространственных гармоник резко уменьшается с увеличением номера гармоники, то в ЛОВ используются обычно такие замедляющие системы, в которых обратная пространственная гармоника является основной гармоникой либо минус первой. Пусть в ЛОВ электронный поток взаимодействует с полем первой обратной пространственной гармоники, фазовая скорость которой совпадает с направлением движения электронов и из (4.6) и равна ![]() . Для эффективного взаимодействия, так же как и в ЛБВ, скорость электронного потока ve должна немного превышать скорость волны vф(-1). Будем считать ve ≈ vф(-1).
. Для эффективного взаимодействия, так же как и в ЛБВ, скорость электронного потока ve должна немного превышать скорость волны vф(-1). Будем считать ve ≈ vф(-1).
Электроны группируются в сгустки, которые расположены в области тормозящего поля, и отдают при торможении часть кинетической энергии электромагнитной волне. При этом энергия в замедляющей системе в соответствии с направлением групповой скорости распространяется навстречу электронному потоку, т. е. от коллектора к пушке. Поэтому в ЛОВ вывод энергии необходимо располагать возле электронной пушки. Поглотитель в ЛОВ необходим для предотвращения возбуждения на прямой гармонике, а также для устранения влияния отражений от нагрузки. Если ЛОВ на выходе плохо согласована с нагрузкой, то отраженная волна возвращается в пространство взаимодействия и двигается к коллектору взаимодействия с электронным потоком, так как не выполняется условие синхронизма. Затем она отражается от конца замедляющей системы у коллектора (если там нет поглотителя) двигается к выходу ЛОВ и взаимодействует с электронным потоком. На выходе суммируются мощности основной волны и отраженной. Если фазы этих волн совпадают, то выходная мощность возрастает, если противоположны — то уменьшается. Поэтому при отсутствии поглотителя наблюдаются колебания выходной мощности в рабочем диапазоне частот.
Распространение энергии в направлении, обратном направлению движения электронного потока, создает внутреннюю положительную обратную связь между полем волны и потоком электронов. Эта связь распределена во всем пространстве взаимодействия. Часть энергии волны возвращается электронному потоку, что способствует дальнейшему группированию потока и возникновению автоколебательного режима.
Частоту колебаний автоколебательной системы с внешней цепью обратной связи обычно находят из условия баланса фаз, т.е. из условия, что суммарный сдвиг фазы в замкнутом контуре, определяющем усиление и обратную связь, кратен 2π. Такой подход не возможен в ЛОВ с распределенной обратной связью, так как в ней много петель обратной связи, и обратная связь осуществляется на любом элементе длины замедляющей системы. Поэтому фазовое условие самовозбуждения колебаний свяжем с условием наилучшей передачи энергии от электронного потока СВЧ полю. Это условие состоит в том, что образовавшийся сгусток электронов не должен выходить из тормозящего поля электромагнитной волны. Другими словами, необходимо, чтобы относительный сдвиг фаз ∆φ волны и сгустка не превышал π т. е.
![]() (4.22)
(4.22)
где ![]() определяет сдвиг фаз, создаваемый волной обратно пространственной гармоники, a
определяет сдвиг фаз, создаваемый волной обратно пространственной гармоники, a ![]() — электронным потоком.
— электронным потоком.
Очевидно, что в общем случае ∆φ может быть равно нечетному числу π:
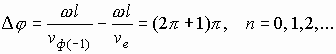 (4.23)
(4.23)
Число n называют порядком колебаний в ЛОВ или номером зоны колебаний. Например, для зоны n = 1, ∆φ=3π, поэтому 2/3 пути электронные сгустки проходят в тормозящем, а 1/3 — в ускоряющем полях, отбирая на этом участке энергию от поля волны.
В связи с этим результирующая энергия, передаваемая от электронного потока полю, становится меньше, чем в зоне n = 0, которую обычно называют основной. Если путем изменения ускоряющего напряжения U0 изменить скорость движения электронов ve, то (4.23) будет выполняться уже для другого значения фазовой скорости vф(-1) обратной пространственной гармоники. Например, с увеличением U0 скорость электронов ve возрастает и для выполнения (4.23) необходимо увеличение vф(-1). Так как дисперсия фазовой скорости обратных пространственных гармоник аномальная, то фазовая скорость vф(-1) возрастает при увеличении частоты. Таким образом, увеличение U0 приводит к увеличению частоты генерируемых колебаний. Этим и объясняется электронная перестройка частоты генерируемых колебаний.
Генерация колебаний в ЛОВ начинается при определенном минимальном значении анодного тока, который называется пусковым. При этом мощность возбуждаемых колебаний в ЛОВ превышает потери мощности в замедляющей системе (условие баланса амплитуд). Пусковой ток, требуемый для начала самовозбуждения, увеличивается с ростом номера n.
В [13] получены приближенные формулы для определения пускового тока ЛОВ и электронного КПД: Iп ≈ 0,124U0/RсвN3; ηэ ≈ 0,84C.
Пусковой ток уменьшается с увеличением сопротивления связи Rсв замедляющей системы, а также с увеличением электрической длины замедляющей системы. Параметр усиления С в ЛОВ мал, поэтому электронный КПД составляет примерно несколько процентов. На рис. 4.9 приведена зависимость КПД ЛОВ от отношения рабочего тока I0 к пусковому. По оси ординат отложено отношение нормированного значения КПД к параметру С. Данная зависимость получена в результате решения уравнений нелинейной теории ЛОВ.
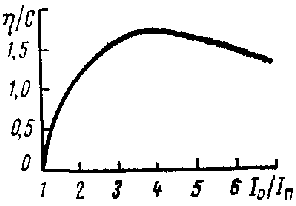 Рис. 4.9
Рис. 4.9
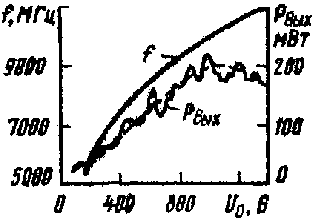 Рис. 4.10
Рис. 4.10
При увеличении рабочего тока увеличиваются входная мощность и соответственно КПД.
Максимальное значение КПД получается при отношении I0/Iп=3÷5. Затем при увеличении рабочего тока КПД и выходная мощность уменьшаются.
Важной характеристикой ЛОВ является зависимость выходной Мощности и частоты генерируемых колебаний от ускоряющего напряжения (рис. 4.10). С увеличением ускоряющего напряжения частота генерируемых колебаний увеличивается, т. е. имеет место электронная перестройка частоты генерируемых колебаний. Частотная характеристика ЛОВ является нелинейной. Закон изменения частоты обусловлен дисперсией замедляющей системы. Ширина рабочего диапазона электронной перестройки частоты генератора на ЛОВ определяется характеристиками замедляющей системы и допустимыми пределами изменения выходной мощности. При коаксиальном выводе энергии ЛОВ имеют коэффициент перекрытия диапазона δп ≈ 2, а с волноводным выводом — δп ≈ 1,5÷1,6.
Для характеристики зависимости частоты от напряжения удобно пользоваться понятием крутизны электронной перестройки частоты: S=df/dU0. Для ЛОВ сантиметрового диапазона крутизна —- не больше нескольких мегагерц на вольт, а для миллиметрового — десятки мегагерц на вольт.
Рассмотрим теперь зависимость выходной мощности от ускоряющего напряжения. Сначала Рвых растет, так как увеличивается подводимая в ЛОВ мощность постоянного тока P0=I0U0, а затем в связи с увеличением Iп рост Рвых замедляется, возможно наступление насыщения и даже спада. Кривая выходной мощности весьма изрезана вследствие отражений от поглотителя и недостаточного согласования замедляющей системы с выходным волноводом.
Лампа обратной волны может быть использована также как усилитель. В этом случае рабочий ток лампы должен быть меньше пускового. Процесс усиления в ЛОВ аналогичен процессу усиления в ЛБВ, только сигналы усиливаются в направлении, противоположном направлению движения электронов. Поэтому вход лампы расположен возле коллектора, а выход, как и в генераторе, — около электронной пушки. Такой усилитель является регенеративным. Кривая усиления имеет вид узкой резонансной кривой, центр которой определяется условием синхронизма. При изменении ускоряющего напряжения условие синхронизма будет выполняться для другой частоты, и кривая усиления смещается по оси частот. Такое свойство усилительной ЛОВ позволяет использовать ее в качестве селективного усилителя с высокой избирательностью по частоте и электронной перестройкой резонансной частоты в широких пределах. Однако усилительные ЛОВ применяются мало.
Лампы обратной волны применяются в качестве гетеродинов радиолокационных и связных приемников, в задающих генератоpaх передатчиков РЛС с быстрой перестройкой частоты и широкополосных ЧМ системах передачи данных, в свипгенераторах измерительной аппаратуры. Разработаны ЛОВ для диапазона часто от 0,5 до 870 ГГц. Основное достоинство ЛОВ, как уже было сказано, заключается в возможности электронной перестройки частот ты в широкой полосе. Однако ев последние годы в связи с крупными достижениями в области полупроводниковых приборов СВЧ начался процесс замены ЛОВ во вновь разрабатываемой аппаратуре на частотах до 10—12 ГГц на полупроводниковые генератору СВЧ. На более высоких частотах вместо ЛОВ все чаще используются генераторы на диодах Ганна. Полупроводниковые генераторы на диодах Ганна уже имеют предельную частоту 94 ГГц, а на ЛПД — 110 ГГц. Проводятся также, разработки этих приборов для более высоких частот.
В настоящее время выпускаются ЛОВ в основном для замены вышедших из строя в уже существующей аппаратуре. Максимальная выходная мощность ЛОВ составляет 100 Вт на частоте 30 ГГц, 1 Вт на частоте 70 ГГц и 10 мВт на частоте 400 ГГц. Новые типы ЛОВ разрабатываются только в субмиллиметровом диапазоне. Так, недавно закончилась разработка ЛОВ в полосе частот 340— 400 ГГц с выходной мощностью, превышающей 10 мВт, рабочее напряжение изменяется от 4 до 8 кВ. Эта ЛОВ предназначена для применения в космической аппаратуре. В приборе использован магнит из сплава самарий-кобальт, масса прибора 10 кг.
Контрольные вопросы.
- Объясните принцип длительного взаимодействия электронного потока с волной.
- При каком соотношении скорости электронов и фазовой скорости возможен отбор энергии у электронного потока?
- Что такое дисперсия. Перечислите основные виды дисперсии?
- Что такое пространственные гармоники? Какими параметрами они отличаются?
- Объяснить схематическое устройство и принцип действия ЛБВ.
- Объяснить назначение и работу основных узлов ЛБВ (электронной пушки, замедляющей системы, фокусирующей системы, коллектора, поглотителя СВЧ энергии).
- Каким образом устраняется самовозбуждение ЛБВ?
- Объясните зависимость РВЫХ от тока луча, ускоряющего напряжения.
- От каких факторов зависит рабочая полоса частот усилительной ЛБВ?
- Объясните амплитудную и амплитудно-частотную характеристики ЛБВ.
- Какие методы используются для повышения КПД?
- Каковы причины шумов ЛБВ? Какие меры предпринимаются для ослабления шумов?
- Перечислите преимущества и недостатки фокусирующих систем различного типа.
5. Полупроводниковые диоды и транзисторы СВЧ
5.1. Классификация полупроводниковых СВЧ диодов. Особенности работы полупроводниковых диодов в диапазоне СВЧ
Сверхчастотный полупроводниковый диод (СВЧ-диод) – это полупроводниковый диод, предназначенный для преобразования и обработки сверхчастотного сигнала.
Полупроводниковые СВЧ-диоды уже длительное время применяют в различной радиоэлектронной аппаратуре и измерительной технике СВЧ-диапазона, т.е. на частотах более 300 МГц. Сначала СВЧ-диоды использовали для детектирования и смещения сигналов. Для этих целей применяли точечные диоды, выпрямляющий электрический переход в которых возникал между кристаллом полупроводника и прижимным металлическим электродом в виде заостренной пружинки. Созданные в последнее время новые типы СВЧ-диодов практически целиком заменили точечные детекторные и смесительные диоды. Они дают возможность решать задачи генерации и усиления электромагнитных колебаний СВЧ-диапазона, умножения частоты, модуляции, регулирования, ограничения сигналов и т.п.
На сверхвысоких частотах могут работать такие СВЧ-диоды как детекторные, смесительные, параметрические, настроечные, переключательные, лавинно-пролетные, генераторы Ганна и др.
5.2. Детекторные диоды СВЧ
Детекторный полупроводниковый диод – это полупроводниковый диод, предназначенный для детектирования сигнала.
При детектировании используется выпрямляющее свойство диода для выделения из модулированных по амплитуде ВЧ- или СВЧ-колебаний сигнала более низкой частоты, который потом поступает на вход усилителя (рисунок).
Одним из основных параметров детекторных СВЧ-диодов является чувствительность по току b 1 – отношение приращения выпрямленного тока при заданной нагрузке в выходной цепи диода к мощности СВЧ-сигнала, подводимой ко входу диодной камеры с детекторным диодом в рабочем режиме и вызвавшей это приращение. Чувствительность по току детекторного диода зависит от постоянного прямого тока смещения. Наибольшие значения чувствительности по току обычно получаются при прямом токе смещения в несколько десятков микроампер, но при выборе тока смещения необходимо учитывать его влияние и на другие параметры.
Обобщенным параметром детекторного диода, учитывающим различные свойства диода и следующего за ним усилителя (видеоусилителя), является коэффициент качества детекторного диода, который характеризует чувствительность приемного устройства с детекторным диодом и определяется по формуле: 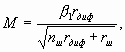 где rдиф – дифференциальное сопротивление диода при определенном положительном смещении; nш – шумовое отношение СВЧ-диода; rш – эквивалентное шумовое сопротивление видеоусилителя, которое обычно принимают при расчетах равным 1 кОм.
где rдиф – дифференциальное сопротивление диода при определенном положительном смещении; nш – шумовое отношение СВЧ-диода; rш – эквивалентное шумовое сопротивление видеоусилителя, которое обычно принимают при расчетах равным 1 кОм.
Лучшие детекторные СВЧ-диоды имеют коэффициент качества более 100 Вт –1/2. К таким диодам можно отнести, например, диоды Шоттки с планарно-эпитаксиальной структурой на основе арсенида галлия АА204А…АА204В, предназначенные для детектирования в сантиметровом диапазоне длин волн.
5.3. Смесительные диоды СВЧ
Смесительный полупроводниковый диод – это полупроводниковый диод, предназначенный для преобразования высокочастотных сигналов в сигнал промежуточной частоты.
К смесительному диоду подводится сигнал и напряжение от специального генератора – гетеродина. В связи с нелинейностью ВАХ диода происходит образование сигнала разностной (промежуточной) частоты. Дальнейшее усиление входного сигнала осуществляется на этой промежуточной частоте, которая должна быть выше частот, соответствующим низкочастотным шумам, обратно пропорциональным частоте.
![]() Основным параметром смесительных диодов, определяющим эффективность преобразования входных сигналов высокой частоты в сигналы промежуточной частоты, является параметр Lпрб называемый потери преобразования смесительного диода и равный отношению мощности СВЧ-сигнала на входе диодной камеры к мощности сигнала промежуточной частоты, выделяемой в нагрузке смесительного диода в рабочем режиме:
Основным параметром смесительных диодов, определяющим эффективность преобразования входных сигналов высокой частоты в сигналы промежуточной частоты, является параметр Lпрб называемый потери преобразования смесительного диода и равный отношению мощности СВЧ-сигнала на входе диодной камеры к мощности сигнала промежуточной частоты, выделяемой в нагрузке смесительного диода в рабочем режиме:
В большинстве приемных устройств СВЧ-диапазона отсутствуют усилители перед смесителем. Поэтому чувствительность всего приемного устройства, возможность различить полезный сигнал на фоне шумов зависят от уровня шумов смесительного диода. Уровень шумов смесительного диода (и других приборов) оценивают шумовым отношением nш – отношением номинальной мощности шумов диода в рабочем режиме к номинальной мощности тепловых шумов соответствующего активного сопротивления при той же температуре и одинаковой полосе частот.
Другим параметром, характеризующим шумы смесительного диода и других приборов и систем, является коэффициент шума – отношение мощности шумов на выходе к той ее части, которая вызвана тепловыми шумами источника сигнала:
![]()
![]() Обобщенным параметром приемного устройства, в смесителе которого использован диод с определенными потерями преобразования и шумовым соотношением, является нормированный коэффициент шума – значение коэффициента шума приемного устройства со смесительным диодом на входе при коэффициенте шума усилителя промежуточной частоты Fупч, равном 1,5 дБ:
Обобщенным параметром приемного устройства, в смесителе которого использован диод с определенными потерями преобразования и шумовым соотношением, является нормированный коэффициент шума – значение коэффициента шума приемного устройства со смесительным диодом на входе при коэффициенте шума усилителя промежуточной частоты Fупч, равном 1,5 дБ:
Одним из вспомогательных параметров смесительных диодов служит выпрямительный ток Iвп – постоянная составляющая тока, протекающая в выходной цепи диода в рабочем режиме. Этот параметр используется для контроля исправности смесительного диода и гетеродина приемника, от которого на смесительный диод подается определенная мощность СВЧ-колебаний с определенной длинной волны.
Другим вспомогательным параметром является коэффициент стоячей волны по напряжению СВЧ-диода Kст U – коэффициент стоячей волны по напряжению в передающей линии СВЧ, когда она нагружена на определенную диодную камеру с СВЧ-диодом в рабочем режиме. Чем лучше согласовано входное сопротивление камеры (с диодом) с волновым сопротивлением тракта, тем меньше коэффициент стоячей волны по напряжению и потери принимаемого сигнала.
5.4. Переключательные диоды СВЧ
Переключательный полупроводниковый диод – это полупроводниковый диод, предназначенный для применения в устройствах управления уровнем сверхвысокочастотной мощности.
Принцип действия переключательного диода основан на большом различии полного сопротивления СВЧ-сигналу при прямом постоянном токе через диод и при обратном постоянном напряжении на диоде. Именно поэтому СВЧ-тракт (волноводная, коаксиальная или полосковая линия), следующий за переключательным устройством с диодом, может быть либо открыт, либо закрыт для СВЧ0сигнала. Например, в радиолокационных станциях с фазированными решетками, содержащими тысячи идентичных антенных элементов, переключательные диоды должны обеспечить подачу мощного СВЧ-импульса на каждый элемент в определенные моменты времени. При этом мощные импульсы передатчика не должны попадать в канал чувствительного приемника.
Отсюда ясны основные требования к переключательным СВЧ-диодам. Они должны с минимальными потерями пропускать СВЧ-мощность в состоянии пропускания и не пропускать – в состоянии запирания, обладать большой допустимой мощностью рассеяния, большим пробивным напряжением, малой собственной емкостью и достаточно большой скоростью переключения.
Обобщенным параметром переключательного диода является критическая частота fкр, которая характеризует эффективность переключательного диода и определяется по формуле: ![]() где Сстр – емкость структуры; rпр – прямое сопротивление потерь (активная составляющая полного сопротивления диода) при определенном прямом токе смещения; rобр – обратное сопротивление потерь при определенном обратном напряжении смещения.
где Сстр – емкость структуры; rпр – прямое сопротивление потерь (активная составляющая полного сопротивления диода) при определенном прямом токе смещения; rобр – обратное сопротивление потерь при определенном обратном напряжении смещения.
Для увеличения допустимой мощности рассеяния диода необходимо увеличивать площадь выпрямляющего электрического перехода, что влечет за собой увеличение барьерной емкости. Поэтому большинство переключательных СВЧ-диодов имеет p-i-n-структуру, толщина p-n-перехода которой существенно увеличена из-за наличия между p- и n-областями слоя высокоомного полупроводника с собственной электропроводимостью (рисунок).
Практически p-i-n-структуру для переключательных СВЧ-диодов формируют на исходном кристалле кремния с проводимостью, близкой к собственной, т.е. либо с небольшой концентрацией акцепторов (p -слой), либо с небольшой концентрацией доноров (n -слой). Энергетическая диаграмма, распределение примесей, плотность объемного заряда и электрического поля в p-i-n- и p-p -n-структурах показаны на рисунке. Методы формирования этих структур различны: вплавление и диффузия примесей, эпитаксиальное наращивание, ионное легирование.
Диоды с p-i-n-структурой отличаются меньшей барьерной емкостью, которая к тому же очень слабо зависят от напряжения (особенно при больших концентрациях примесей в p- и n-областях). Практическая независимость емкости структуры от напряжения оказывается важным свойством переключательных диодов, так как изменение емкости с напряжением может вызвать дополнительные частотные искажения полезного сигнала.
Пробивное напряжение диодов с p-i-n-структурой достигает нескольких сотен вольт, что существенно превышает пробивное напряжение диодов с обычным p-n-переходом и с таким же уровнем легирования прилегающих областей.
Для переключательных СВЧ-диодов некоторых марок (2А523А-4 и др.) максимально допустимая мощность, которую может рассеять диод в непрерывном режиме, равна 20 Вт. Такие диоды представляют собой бескорпусные приборы с жесткими выводами – кристаллодержателями – и защитным покрытием. Диаметр их 2 мм, длина 3,6 мм.
Переключательный СВЧ-диод может работать при последовательном и при параллельном включении с линией передачи. В параллельной схеме при прямом смещении диод имеет небольшое сопротивление, шунтирующее линию, и большая часть СВЧ-мощности отражается обратно. Таким образом, при параллельной схеме для переключения СВЧ-тракта используют разницу в отражении, а не в поглощении. В самом диоде при этом поглощается незначительная часть падающей на него СВЧ-мощности, что позволяет относительно маломощному прибору управлять десятками и сотнями киловатт импульсной СВЧ-мощности.
Недостатками переключательных СВЧ-диодов с p-i-n-структурой является инерционность процесса рассасывания носителей заряда (электронов и дырок) из i-слоя при переключении диода с прямого направления на обратное, так как толщина i-слоя может составлять несколько десятков микрометров, а скорость движения носителей заряда ограничена.
Значительно большую скорость переключения можно получить при использовании диодов Шоттки, изготовленных на основе арсенида галлия. Однако уровень переключаемой СВЧ-мощности при этом на несколько порядков ниже, чем при применении переключательных СВЧ-диодов с p-i-n-структурой.
5.5. Биполярные СВЧ транзисторы
Граничная частота. Частотные свойства транзисторов обычно характеризуются граничной частотой fгр, которая связана со временем задержки сигнала τ от эмиттера до коллектора:
fгр =1/2πτ (5.1)
Время задержки
τ = τэ.п+ τб + τк.п+ τк, (5.2)
где τэ.п — время зарядки емкости эмиттерного перехода; τб — время пролета носителей заряда через базовую область; τк.п — время задержки в коллекторном переходе, связанное с временем пролета; τк — время зарядки емкости коллекторного перехода.
Уменьшение ширины базовой области примерно до 0,1 мкм снижает τб до единиц пикосекунд. В этом случае граничная частота в основном будет определяться τэ.п и τк.п, которые примерно равны 10 пс. Поэтому для увеличения fгр необходимо выдвигать дополнительные требования: уменьшение емкости эмиттерното перехода Сэ.п, ширины коллекторного перехода dк и сопротивления коллекторной области rк, влияющего на значение τ к.
Однако требования, предъявляемые к СВЧ транзисторам, противоречивы. Например, повышение концентрации примеси, необходимое для уменьшения ширины коллекторного перехода (уменьшения dк), приводит к росту емкости этого перехода. Уменьшение площади перехода для снижения его емкости будет сопровождаться падением мощности транзистора. Необходимого уменьшения величин rк и dк можно добиться повышением концентрации примеси, но при это τ м произойдет сужение коллекторного перехода, увеличится емкость, а кроме того, снизится напряжение пробоя и выходная мощность. Таким образом, повышение граничной частоты биполярного транзистора сопровождается падением мощности и важнейшим ограничением является напряжение пробоя коллекторного перехода, которое зависит и от выбора полупроводникового материала.
Рассмотрим предельный случай, когда граничная частота определяется только временем задержки сигнала в коллекторном переходе τк.п, т. е.
fгр =1/2π τк.п (5.3)
Доказано, что τк.п примерно равно половине времени пролета носителей в коллекторном переходе (τк.п ≈ τпр/2).
Дрейфовая скорость при увеличении напряженности поля сначала возрастает линейно, а затем стремится к предельному значению, называемому скоростью насыщения vн. Эта зависимость скорости от напряженности доля объясняется в § 7.1. Скорость vн определяется материалом полупроводника и типом носителей заряда (электрон, дырка). Так как дрейфовая скорость носителей в переходе не может превышать значения vн, то минимальное время пролета τпр=dк /vн а максимальная граничная частота (5.3)
fгр = vн /π dк (5.4)
Предположим, что поле Е в переходе однородное, а его значение, соответствующее началу пробоя, Епpoб. Тогда напряжение на переходе в начале пробоя Uпpoб ≈ Епpoб dк и (6.4) преобразуете к виду
fгр Uпpoб ≈ Епpoб vн /π (5.5)
Максимальная напряженность поля Епpoб и Uпpoб, связанные между собой, зависят от концентрации примеси и формы перехода. С ростом концентрации Епpoб увеличивается, а Uпpoб уменьшается. При увеличении концентрации примеси в резком переходе от 1014 до 1017 см -3 Епpoб изменяется в следующих пределах: у германия (1,5 — 3,1)•106 В/см, у кремния (3 — 6)•106 В/см, а у арсенида галлия (3,5—6,5)•106 В/см. Таким образом, Епpoб и Uпpoб у Si и GaAs почти одинаково и в 1,5 — 2 раза больше, чем у Ge. Скорость насыщения vн для электронов и дырок соответственно в Ge 6•106 и 8•106 см/с, в Si примерно равны 107 см/с, в GaAs — около 9•106 см/с. Произведение (5.5) составит для Ge, Si и GaAs примерно 200, 400 и 450 ГГц•B соответственно. Эти результаты можно заменить одним условием, ограничивающим частоту fгр:
fгрUпpoб ≤ 200ГГц•В.
При минимальном напряжении пробоя 2 В частота fгр ≈ 100 ГГц. Однако этот результат не может быть получен, так как в переходе значение поля не постоянно, а скорость не везде равна скорости насыщения. Кроме того, существуют конструктивные и технологические ограничения. Поэтому считают, что fгр. max ≈ 20 ГГц.
Влияние уровня инжекции на граничную частоту. На пути создания транзисторов с узкой базой имеются ограничения, связанные с большой плотностью тока в мощных транзисторах.
Одно из них состоит в том, что при большой плотности тока эмиттера возрастает напряжение, создаваемое базовым током на сопротивлении узкой базовой области (рис. 5.4). Если базовый электрод окружает эмиттер, то прямое напряжение на переходе в центре эмиттера, расстояние I от которого до базового электрода наибольшее (базовое сопротивление максимально), оказывается меньше, чем на периферии эмиттера. Поэтому ток в переходе будет существовать по периметру (эффект оттеснения тока эмиттера к периферии эмиттера). В этом случае площадь эмиттера используется неэффективно, в то время как емкость перехода определяется полной площадью. Таким образом, в мощных транзисторах целесообразно использовать очень узкие эмиттеры с большим общим периметром. Ширина эмиттерных полосок при плотности тока примерно 1000 А/см2 выбирается порядка нескольких микрометров.
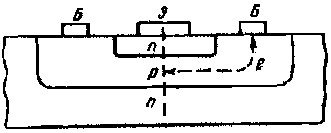 Рис. 5.4
Рис. 5.4
 Рис. 5.5
Рис. 5.5
Еще одним ограничением при создании узкой базы в транзисторах с большой плотностью тока является смещение границы базовой области в сторону коллекторной области. При большой плотности тока в pnp-транзисторе концентрация дырок в коллекторном переходе становится сравнимой с концентрациями донорной и акцепторной примесей. В сечении, где распределение объемного заряда в переходе проходило ранее через нуль, теперь будет существовать положительный заряд дырок. Это означает, что весь коллекторный 'переход сместился в сторону коллекторной области, т. е. увеличилась ширина базовой области. Последнее приводит к росту рекомбинации инжектированных дырок в базовой области, снижению коэффициента передачи тока и уменьшению граничной частоты fгр вследствие роста времени пролета носителей в базовой области.
При большой плотности тока приходится также учитывать влияние сопротивления коллекторной области, так как обычно последняя является высокоомной и изготавливается путем эпитаксиального наращивания n-слоя на низкоомной подложке (n+-область). На рис. 6.5 показано типичное распределение концентрации основных носителей заряда в транзисторе с высокоомной коллекторной областью, которая необходима для уменьшения емкости коллекторного перехода и повышения напряжения пробоя. Однако с ростом коллекторного тока увеличивается падение напряжения на сопротивлении эпитаксиальной коллекторной n-области и напряжение на самом переходе уменьшается. Это вызовет уменьшение ширины коллекторного перехода, т. е. нежелательное расширение базовой области. При некотором токе коллектора напряжение на переходе пройдет через нулевое значение и транзистор из активного (усилительного) режима перейдет в режим насыщения.
Технологические ограничения. Формула (5.5) устанавливает для граничной частоты теоретический предел, который пока не достигнут. При выборе полупроводникового материала предпочтение отдается кремнию по технологическим соображениям. Главное преимущество кремния состоит в том, что появляющаяся на нем двуокись кремния может использоваться как маска в процессе диффузии примесей или как изолирующее диэлектрическое покрытие. Окислы германия и арсенида галлия менее стабильны, чем двуокись кремния.
Важными электрофизическими свойствами полупроводников, определяющими параметры транзистора, являются подвижность электронов и дырок, диэлектрическая постоянная и теплопроводность. Подвижность определяет время пролета носителей, в базе и сопротивления областей базы и коллектора. Чем меньше эти величины, тем выше коэффициент усиления и меньше коэффициент шума транзистора на СВЧ.
В GaAs подвижность электродов примерно в 4 раза больше, чем в кремнии, и поэтому GaAs является более предпочтительным материалом. Однако из-за технологических трудностей он не получил применения в биполярных транзисторах.
Диэлектрическая постоянная, влияющая на емкость переходов составляет для кремния, арсенида галлия и германия 11,7; 11,1 и 16 соответственно. Но по теплопроводности кремний в 2 раза превосходит GaAs и поэтому обычно используется для изготовления мощных транзисторов.
Сравнивая же кремний и германий, следует отметить такие преимущества кремния, как более высокая скорость насыщения электронов и большая напряженность поля пробоя.
Технология изготовления приборов на основе кремния хорошо разработана и позволяет создавать СВЧ транзисторы с высоким процентом выхода годных и с хорошей надежностью. Глубину диффузии примесей (мышьяка, фосфора и бора) в кремнии можно контролировать при планарной технологии с точностью 0,1 мкм, а достижимые на практике уровни легирования оказались особенно удобными для создания кремниевых nрn -транзисторов.
Выполняются СВЧ транзисторы по планарной технологии таким образом, чтобы отношение периметра эмиттера к его площади было наибольшим. Последнее достигается в транзисторе с гребенчатой и многоэмиттерной структурами и в многоструктурных транзисторах. В гребенчатой структуре (рис. 6.6 а) чередуются эмиттерные и базовые области, имеющие форму узких полосок. В многоэмиттерной структуре (ряс. 5.6 б) вместо каждой эмиттерной полосковой области используется ряд небольших прямоугольных эмиттеров, соединенных металлическими полосками. Между эмиттерами находятся полосковые выводы от общей базовой области. Применяются также многоструктурные транзисторы, которые по существу являются объединением ряда многоэмиттерных или гребенчатыхсекций.
а) б)
Рис. 5.6
Отношение периметра к площади эмиттера с гребенчатой структурой доходит до 250 мм/мм2. Дальнейшее увеличение отношения требует изготовления полосок с шириной менее 1 мкм.
Для СВЧ транзисторов большое значение имеет точность воспроизведения элементов — ширины эмиттерных полосок, расстояния между эмиттерными и базовыми полосками, коллекторных площадок. Максимальная разрешающая способность при фотолитографии соответствует получению ширины эмиттерных полосок 1 мкм. Для воспроизведения меньших размеров следует применять электронно-лучевую литографию. Вследствие меньшей длины волны электронного излучения можно получить полоски и промежутки с разрешением 0,1 мкм, что позволяет повысить рабочую частоту транзистора.
Для мощных СВЧ транзисторов важной является задача равномерного распределения тока и теплоотвода. В этих транзисторах наблюдается вторичный пробой (первичным называют пробой коллекторного перехода при обратном напряжении эмиттерного перехода) - Вторичный пробой может следовать за первичным, но может возникать самостоятельно при прямом включении эмиттерного перехода.
Вторичный пробой коллекторного перехода связан с перераспределением тока в сечении прибора и его концентрацией в локальных областях. Вторичный пробой характеризуется резким увеличением коллекторного тока и, как правило, приводит к выходу прибора из строя из-за образования локальных областей перегрева. В случае прямого включения эмиттерного перехода перераспределение тока может быть связано с оттеснением тока эмиттера к периферии, с неравномерностью инжекции, вызванной неодинаковостью падения напряжения на различных эмиттерных полосках или наличием дефектов структуры.
Применение гребенчатой и многоэмиттерной структур обеспечивает и равномерность распределения тока. Однако для улучшения равномерности последовательно с полосковыми эмиттерами в гребенчатой структуре или полосками в многоэмиттерной структуре включаются резисторы, ограничивающие ток при прямом включении эмиттерного перехода. Для борьбы со вторичным пробоем при обратном включении эмиттерного перехода следует затруднить развитие первичного (лавинного) пробоя коллекторного перехода. С этой целью эпитаксиальный высокоомный слой коллекторной области делают достаточно толстым. Следует также снижать тепловое сопротивление участка коллекторный переход – корпус.
Параметры биполярных СВЧ транзисторов. Основными параметрами являются рабочая частота, коэффициент усиления по мощности, выходная мощность, КПД и коэффициент шума. При этом коэффициент шума важен только для маломощных (малошумящих) транзисторов, а КПД — для мощных СВЧ транзисторов.
На граничной частоте fгр, при которой коэффициент передач по току в схеме с общим эмиттером равен единице, имеется еще значительное усиление по мощности. Поэтому дополнительно используется характеристическая частота fmax — максимальная частота генерации, на которой коэффициент усиления по мощности равен единице при условии компенсации действия внутренней обратной связи (без внесения потерь) и согласования на входе и выходе. В этом случае:
![]() (5.6)
(5.6)
где r'б — объемное сопротивление базы; Ск — емкость коллекторного перехода; α0 — коэффициент передачи тока эмиттера(h21б).
Если ширины эмиттерных, базбвых полосок и промежутков между ними одинаковы и равны s, длина l, а удельные (на единицу площади) сопротивление базы r0 и емкость коллектора С0, то r'Б ≈ r0s/l, Cк ≈ С0sl. Поэтому (5.6) приводится к виду:
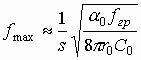
Следовательно, fmax увеличивается с уменьшением размера s. Это подтверждает необходимость уменьшения ширины полосок и зазоров в транзисторных структурах.
Зависимость коэффициента шума от частоты показана рис. 5.7 горизонтальный участок кривой объясняется в основном тепловыми шумами объемного сопротивления базы r'б. Чем выше граничная частота транзистора fгр, тем протяженней участок кривой с наименьшим коэффициентом шума. Коэффициент шума зависит также от сопротивления источника сигнала, при этом существует оптимальное сопротивление при котором Kш достигает минимального значения. Существует также оптимальное значение тока эмиттера. Следует отметить, что условия, при которых коэффициент шума имеет минимальное значение, могут не совпадать с условиями получения максимального коэффициента усиления.
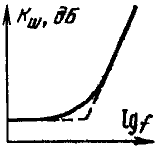
Рис. 5.7
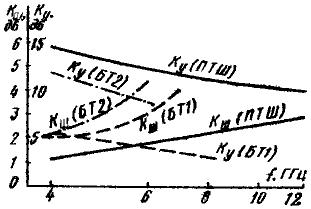
Рис. 5.8
На рис. 5.8 приведены для различных частот значения коэффициентов усиления Ку и шума Кш маломощных биполярных транзисторов с минимальным коэффициентом шума (БТ1) и с максимальным коэффициентом усиления (БТ2). В диапазоне частот 4 — 8 ГГц Кш min=2÷4 дБ, а Ку max = 5 ÷ 3 дБ. Усилители на малошумящих биполярных транзисторах конкурируют с малошумящими ЛБВ и превосходят последние по шумовым свойствам, габаритам, массе и долговечности.
Выходная мощность мощных биполярных транзисторов при переходе от 1 до 4 ГГц падает от 35 — 40 до 5 Вт. Коэффициенты усиления в этом диапазоне составляют 10 — 5 дБ.
Применение в транзисторных СВЧ генераторах варикапов или ферритовых элементов для электрической перестройки частоты позволяет заменять ими лампы обратной волны. Генераторы с варикапами обладают большой скоростью, но малой линейностью перестройки, например ±10%. Если в качестве феррита используется железо-иттриевый гранат (ЖИГ), то линейность перестройки высокая (примерно ±0,3%), но скорость перестройки мала. Диапазон электрической перестройки частоты транзисторных СВЧ генераторов достигает октавы.
5.6. Полевые СВЧ транзисторы
В последние годы возросла роль полевых транзисторов в СВЧ диапазоне, но сравнению с биполярными транзисторами в связи с разработкой полевых транзисторов с барьером Шотки на арсениде галлия. Устройство такого, транзистора показано на рис. 5.9. Затвор представляет собой барьер Шотки, изготовленный на эпитаксиальной пленке из арсенида галлия n-типа. Пленка выращивается на полуизолирующей подложке из того же материала. Затвор, расположенный между истоком и стоком, имеет обычно конфигурацию замкнутого кольца или квадрата. Характерные размеры: ширина затвора 0,2 – 2 мм, длина затвора 0,5 – 2 мкм, толщина эпитаксиальной пленки 0,15 – 0,5 мкм.
Для получения омических контактов истока и стока используются сплавы на основе золота и серебра с соответствующими легирующими добавками. Барьер Шотки получают нанесением металлов (платина, хром, никель, молибден и др.) или сплавов.
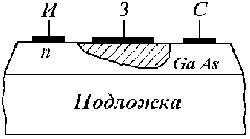
Рис. 5.9
Резкое улучшение частотных свойств полевых транзисторов произошло благодаря применению арсенида галлия с высокой подвижностью электронов, уменьшению длины затвора до 1 мкм и использованию более тонких и более высоколегированных эпитаксиальных пленок арсенида галлия.
Для транзисторов с малой длиной канала частота fmax, на которой коэффициент усиления по мощности равен единице, определяется минимально возможным значением времени пролета τmin, т. е.
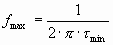 (5.7) Значение τmin соответствует максимальной скорости носителей – скорости насыщения υн , поэтому при длине канала L τ= L/υн , а из (5.6)
(5.7) Значение τmin соответствует максимальной скорости носителей – скорости насыщения υн , поэтому при длине канала L τ= L/υн , а из (5.6) 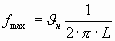 (5.8)
(5.8)
Следовательно, GaAs, имеющий большее значение υн, чем у кремния и германия, является предпочтительным материалом для изготовления полевых транзисторов.
Уменьшение длины затвора приводит к уменьшению времени пролета электронов в канале и к снижению емкости затвора. Эта емкость может быть также уменьшена изготовлением полуизолирующего слоя между затвором и эпитаксиальной пленкой арсенида галлия (каналом).
Важным направлением в разработке маломощных полевых транзисторов с барьером Шотки на арсениде галлия является снижение коэффициента шума. Основные источники шума в этом транзисторе — тепловой шум в канале, индуцированный шум затвора и шум паразитных (пассивных) элементов. Тепловой шум в канале — это тепловой шум сопротивления проводящей части канала. Индуцированный шум затвора является следствием шума в канале, так как любая флуктуация потенциала в канале вызывает флуктуацию напряжения между затвором и каналом. Эти шумы при коротких каналах сильно коррелированны (коэффициент корреляции близок к единице). Шумы пассивных элементов связаны с сопротивлением затвора и истока и по своей природе тепловые. Так как шумы в активной области полевых транзисторов с барьером Шотки очень малы, то шумы пассивных элементов дают больший относительный вклад в общий шум, чем в биполярных транзисторах.
Особенностью полевых транзисторов является большое различие сопротивлений источника сигнала, необходимых для получения максимального коэффициента усиления и минимального коэффициента шума. Это приводит к тому, что при минимальном коэффициенте шума коэффициент усиления примерно в 2 раза меньше максимально возможного. Однако в этом случае коэффициент усиления еще достаточно велик (8 – 15 дБ). Необходимо отметить, что существует также трудность согласования полевого транзистора со стандартным СВЧ трактом, особенно на частотах ниже 1 – 2 ГГц. В связи с этим приходится увеличивать ширину затвора, хотя последнее и приводит к увеличению емкости и сопротивления металлизации затвора.
Существуют полевые транзисторы с коэффициентом шума Кш=З,7 дБ и усиления Ку=12,8 дБ на частоте 10 ГГц. Длина затвора этих транзисторов 0,5 мкм, а ширина 200 мкм. Имеются приборы, у которых Кш=2,6 дБ на частоте 4 ГГц (длина затвора 1,5 мкм, ширина – 1,8 мм).
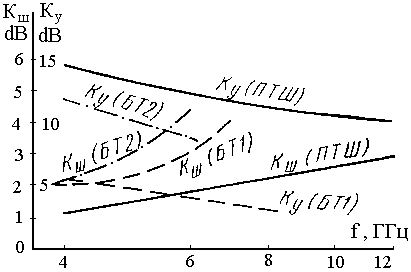
Рис. 5.10
На рис. 5.10 сравниваются коэффициенты усиления Ку и шума Кш полевых транзисторов с барьером Шотки (ПТБШ) и биполярных транзисторов с минимальным коэффициентом шума (БТ1) и максимальным коэффициентом усиления (БТ2).
Для мощных полевых транзисторов требование низкого уровня шума не существенно. Применение арсенида галлия с большой шириной запрещенной зоны (1,4 эВ) позволяет повысить рабочую температуру вплоть до 350°С.
В мощных полевых транзисторах необходимо обеспечить высокое напряжение пробоя затвора, низкоомные контакты истока и стока, а также возможно большее значение периметра истока.
Повышение напряжения пробоя достигается использованием умеренного легирования области канала: 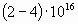 см –3, а также созданием области повышенного сопротивления между затвором и стоком без ухудшения крутизны транзистора. Низкоомные контакты истока и стока получаются путем вплавления пленок золото–германий или созданием низкоомных эпитаксиальных областей (n+-области). Увеличение периметра истока возможно в результате изготовления многоканальных структур с несколькими контактными площадками затвора, так как обычное увеличение длины истока и затвора ухудшает параметры полевого транзистора из-за роста сопротивления металлизации контактов. Существуют сетчатые и гребенчатые затворы, подобно тому, как это делается в биполярных СВЧ транзисторах.
см –3, а также созданием области повышенного сопротивления между затвором и стоком без ухудшения крутизны транзистора. Низкоомные контакты истока и стока получаются путем вплавления пленок золото–германий или созданием низкоомных эпитаксиальных областей (n+-области). Увеличение периметра истока возможно в результате изготовления многоканальных структур с несколькими контактными площадками затвора, так как обычное увеличение длины истока и затвора ухудшает параметры полевого транзистора из-за роста сопротивления металлизации контактов. Существуют сетчатые и гребенчатые затворы, подобно тому, как это делается в биполярных СВЧ транзисторах.
Применение многоканальных структур обеспечивает повышение мощности полевых транзисторов. Созданы варианты мощных многоканальных полевых транзисторов с управляемым p–n–переходом с горизонтальной и вертикальной структурами. В транзисторах с горизонтальной структурой каналы располагаются параллельно полупроводниковой подложке, как на рис. 1, а в транзисторах с вертикальной структурой они перпендикулярны плоскости подложки.
Мощность полевых транзисторов на арсениде галлия с барьером Шотки уже превышает мощность биполярных транзисторов: 1,6 Вт и КПД 45% на частоте 8 ГГц. Ожидается, что в трехсантиметровом диапазоне волн будет получена мощность 10 Вт. Эти транзисторы становятся конкурентами с ЛБВ, имея перед последними преимущество в габаритах, КПД и простоте источников питания.
Наибольшее применение полевые транзисторы на GaAs с барьером Шотки нашли в малошумящих СВЧ усилителях. В диапазоне 4 – 20 ГГц они являются лучшими по шумовым и усилительным характеристикам, чем другие приборы того же назначения. Большой динамический диапазон и хорошие шумовые характеристики позволяют использовать их в смесителях. В последнее время наметилась тенденция к широкому внедрению полевых транзисторов с барьером Шотки в усилителях, предназначенных для замены ламп бегущей волны и в параметрических усилителях. Низкий коэффициент шума, малая пульсация коэффициента усиления (0,05 дБ на 10 МГц), небольшие изменения групповой задержки этих транзисторов позволяют произвести замену ЛБВ в телевизионной системе с частотной модуляцией.
В последнее время значительный интерес проявляется к охлаждаемым усилителям на полевых транзисторах из GaAs с барьером Шотки. Так как шумы в этих приборах в основном имеют тепловую природу, то охлаждение приводит к существенному уменьшению коэффициента шума. При этом, в отличие от биполярных транзисторов, коэффициент усиления увеличивается. Трехкаскадный усилитель для спутниковой связи США в диапазоне 11,7–12,2 ГГц имеет при комнатной температуре коэффициент шума 5,3 дБ, а коэффициент усиления 18 дБ. Охлаждение усилителя до 40 К снижает Кш до 1,6 дБ и увеличивает Ку до 31 дБ, что сравнимо с параметрами неохлаждаемых параметрических усилителей.
Малошумящие усилители на полевых транзисторах из GaAs с барьером Шотки по сравнению с параметрическими усилителями характеризуются простотой настройки, высоким постоянством усиления, большой мощностью насыщения.
Контрольные вопросы.
- Конструктивные особенности полупроводниковых диодов СВЧ.
- Особенности работы полупроводниковых диодов в диапазоне СВЧ.
- Особенности устройства СВЧ биполярных транзисторов (БТ).
- Особенности устройства СВЧ полевых транзисторов (ПТ).
- Факторы, ограничивающие рабочие частоты БТ.
- Факторы, ограничивающие рабочие частоты ПТ.
- Пути улучшения частотных свойств ПТ и БТ.
- Пути повышения выходной мощности БТ и ПТ на СВЧ.
6. Лавинно-пролетные диоды (ЛПД)
6.1. Лавинное умножение носителей заряда
Зависимость дрейфовой скорости от поля. Для последующего рассмотрения полупроводниковых приборов необходимо знать зависимость направленной скорости носителей (дрейфовой скорости) от напряженности электрического поля для кремния и германия. Эта зависимость vдр(Е) показана на рис. 6.1.
Дрейфовая скорость связана с напряженностью поля Е соотношением
vдр(Е) = µЕ (6.1)
где µ — подвижность носителей, пропорциональная среднему времени пробега, носителей между двумя последовательными соударениями с атомами кристаллической решетки.
Чем больше время пробега τ, тем большую скорость направленного движения приобретет носитель в том же электрическом поле. В слабых электрических полях скорость направленного движения много меньше тепловой скорости, поэтому среднее время пробега определяется тепловой скоростью и от напряженности поля практически не зависит. В этом приближении подвижность носителей также не зависит Е, т.е. в (6.1) дрейфовая скорость пропорциональна Е (начальный участок на рис. 6.1). Напряженность Е определяет прибавку энергии носителя к тепловой энергии при термодинамическом равновесии, когда поле отсутствует. Поэтому линейный начальный участок означает также, что дрейфовая скорость пропорциональна разности полной энергии при наличии поля и тепловой энергии носителей при его отсутствии.
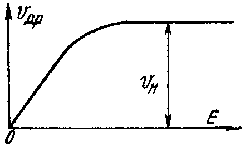
Рис. 6.1
Когда с ростом Е скорость vдр станет сравнимой с тепловой скоростью, время пробега заметно уменьшается, так как длина побега определяется кристаллической решеткой и остается неизменной. Это означает уменьшение подвижности носителей и нарушение в (6.1) пропорциональности между скоростью и напряженностью поля. При больших полях на кривой vдр(Е) появляется участок насыщения. Для объяснения насыщения скорости предполагают, что в сильном поле независимо от его величины носитель заряда при любом соударении с кристаллической решеткой теряет одну и ту же энергию ∆Е. Тогда за 1 с, в течение которой происходит 1/τ соударений, потеря энергии составит ∆Е/τ. Так как рассматривается стационарное состояние, то эта потеря энергии должна восполняться за счет работы силы электрического поля Fэл = еЕ на пути, который за 1 с численно равен дрейфовой скорости, т. е.
∆Е/τ = еЕvдр. (6.2)
кроме этого должен выполняться закон сохранения импульса (количества движения)
Fэл τ = m vдр (6.3)
Из (7.2) и (7.3) следует, что
![]()
Таким образом, если в сильном поле ∆Е от поля не зависит, то дрейфовая скорость также не зависит от него. Это предельное значение дрейфовой скорости называют скоростью насыщения vн. Значение vн зависит от полупроводникового материала и типа носителя (электрон, дырка) и составляет примерно 107 см/с.
Ударная ионизация. Если энергия движущихся в электрическом поле носителей заряда превысит некоторое определенное значение, начнется ударная ионизация: соударение носителя с нейтральным атомом кристаллической структуры приводит к образованию пары новых носителей — электрона и дырки.
Для количественной характеристики этого процесса вводят коэффициенты ионизации an и aр для электронов и дырок — число электронно-дырочных пар, создаваемых на единице пути (1 см) электроном и дыркой соответственно. Коэффициенты an и aр сильно зависят от напряженности поля. Ударная ионизация наблюдается при большой напряженности электрического поля (Е>105 В/см). Зависимость an и aр от напряженности поля для германия, кремния и арсенида галлия показана на рис. 6.2. Увеличение напряженности поля в 2—3 раза может привести к росту коэффициентов ионизации на четыре-пять порядков. В рассматриваемой области значений напряженности поля зависимость an и aр от Е может быть представлена степенной функцией с показателем, лежащим в пределах от 3 до 9 в зависимости от материала и типа носителей. Для арсенида галлия коэффициенты примерно одинаковы (an ≈ aр). У кремния и германия an ≠ aр В дальнейшем для упрощения рассмотрения будем принимать их равными (an =aр =a).
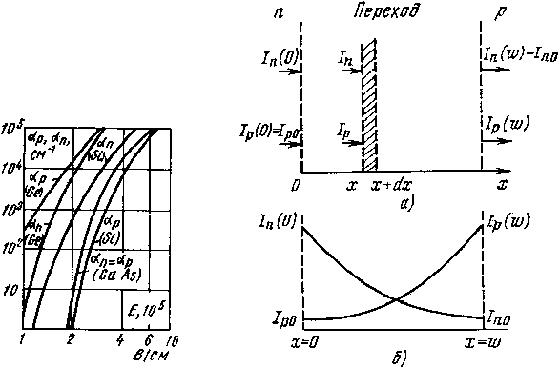
Рис. 6.2 Рис. 6.3
Лавинное умножение носителей в p-n-переходе. В полупроводниковых диодах ударная ионизация может происходить в области p-n-перехода, если в ней создана достаточно большая напряженность поля. С этим явлением связан резкий рост обратного тока перехода, называемый лавинным пробоем.
Ток через переход при обратном напряжении вызван движением неосновных носителей. Дырки, экстрагированные из n-области, двигаются в переходе по направлению к р-области, а электроны, экстрагированные из р-области, перемещаются через переход в n-область. Пусть начальный дырочный ток на левой границе перехода (х = 0) Ip0, а начальный электронный ток на правой границе (x = ω) In0 (рис. 6.3, a). Вследствие ударной ионизации число двигающихся дырок растет слева направо, а электронов — в противоположном направлении. Соответственно в этих направлениях возрастают дырочная и электронные составляющие тока.
Пусть Ip и In дырочный и электронный токи в произвольном сечении х. В слой dx в этом сечении за 1 с слева входит Ip/е дырок, а справа In/е электронов (е —заряд электрона). Каждый носитель, проходя слой dx, создает adx пар носителей (электрон—дырка), если считать коэффициенты ионизации электронов и дырок равными. Поэтому прирост числа дырок на длине dx
d Ip/е = (Ip/е) α dx + (In/e) α dx = (I/e) α dx. (6.4)
где
I =Ip +In (6.5)
— суммарный (полный) ток в переходе, не зависящий от координаты. Тогда из (6.4) приращение дырочного тока в слое
dIp=α Idx. (6.6) Аналогично прирост электронного тока с уменьшением координаты х
dIn = – α Idx. (6.7)
Рассмотрим несимметричный p-n-переход, в котором концентрация акцепторов много меньше концентрации доноров. Концентрация неосновных носителей обратно пропорциональна концентрации примеси, поэтому начальный дырочный ток будет много больше начального электронного тока (Ip0>>In0). В этом случае можно считать, что лавинное умножение вызвано дырками, приходящими из n-области. Интегрируя (6.6) в пределах от х=0 До x=ω θ используя граничные значения токов Ip0 и Ip(ω) получим
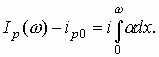 (6.8)
(6.8)
Полный ток I вынесен за знак интеграла, так как он не зависит от координаты. Вследствие лавинного умножения Ip(ω) > Ip0.
В рассматриваемом случае Ip0 >> In0, поэтому Ip(ω) >> In0 и найденный в сечении x=ω οолный ток
I = Ip(ω) + In0 ≈ Ip(ω)
Подставляя в (6.8) I вместо Ip(ω), получим
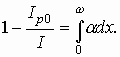
или
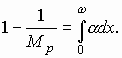 (6.9)
(6.9)
где
Mp= I /Ip (6.10)
—коэффициент лавинного умножения, если процесс умножения в переходе начинается дырками.
Аналогично можно ввести Mn = I / In, если процесс умножения начинают электроны (случай In0 >> Ip0).
Лавинный пробой. Принято считать, что лавинный пробой наступает при таком обратном напряжении на переходе, когда коэффициент лавинного умножения обращается в бесконечность. Если начало лавинного умножения вызвано дырками (Ip0 >> In0), то условие лавинного пробоя можно найти из (6.9), считая, Мр→ ∞. Это возможно при
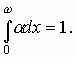 (6.11)
(6.11)
Условие (6.11) имеет простой физический смысл: для возникновения лавинного пробоя необходимо, чтобы каждый электрон и каждая дырка, вошедшие в переход и возникающие в переходе создавали в среднем по одной электронно-дырочной паре. Если aр ≠ an, то носители, имеющие больший коэффициент ионизации должны создавать при прохождении перехода в среднем более одной пары, чтобы скомпенсировать уменьшение коэффициента ионизации носителей другого типа.
Коэффициент α зависит от напряженности поля, распределение которого в переходе можно найти из решения уравнения Пуассона, считая напряженность поля на границах перехода нулевой. Тогда в (6.11) неизвестным будет только ширина перехода ω. Следовательно, можно определить ширину перехода, при которой наступит лавинный пробой, а затем по известному pacпределению напряженности пробоя вычислить напряжение пробоя.
6.2. Пролетный режим работы ЛПД
Принцип работы ЛПД с n+-р-i-р+-структурой. Этот режим работы диода основан на использовании лавинного пробоя и пролетного эффекта носителей в обедненной области различных полупроводниковых структур. Распределение поля в этой области, определяющее физические процессы в диоде, зависит от структуры и закона распределения концентрации примесей в областях структуры. Ниже будет рассмотрена n+-р-i-р+-структурой (диод Рида), так как физические процессы в этом диоде наиболее четко разделены (рис. 6.4, а).
Распределение концентрации примесей в областях структуры показано на рис. 6.4, б. Концентрация примеси в крайних областях р+ и n+ много больше, чем в р-области; по концентрации носителей i-область близка к собственному полупроводнику. Напряженность Е – линейно уменьшается в p-области и остается постоянной в i-области (рис. 6.4, в).
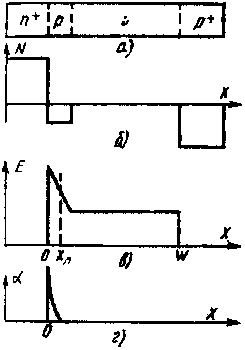 Рис. 6.4
Рис. 6.4
 Рис. 6.5
Рис. 6.5
Вследствие сильной зависимости от напряженности поля коэффициенты ионизации an и aр будут изменяться по направлению х более резко, чем Е (рис. 6.4 г). Зависимость а(х) располагается в пределах р-области. Для упрощения принято an=aр=a. Условие лавинного пробоя (6.11) означает равенство единице площади кривой а(х). Слой умножения, где возможно лавинное умножение носителей, очень узкий и находится в основном справа от сечения х=0, в котором напряженность поля максимальна. Левая граница слоя приблизительно совпадает с сечением x=0. За правую границу условно примем координату xл так, чтобы на участке 0 – xл практически закончилось лавинное умножение. Часть структуры от xл до границы р+-области называют слоем дрейфа. В этой части прибора нет лавинного умножения, но напряженность поля еще достаточно велика, чтобы дрейфовая скорость носителей была равна скорости насыщения vн (см. рис. 6.1)
В условиях генерации или усиления колебаний на ЛПД кроме постоянного напряжения имеется синусоидальное. Поэтому к напряженности поля Е в статическом режиме, показанной на рис. 6.4, в добавляется синусоидально изменяющаяся во времени напряженность ноля Е(t). Если пренебречь влиянием объема заряда, то напряженность переменного поля будет одинаковой во всех точках слоев умножения и дрейфа. В этом случае в данный момент времени отклонение от статического значения поля не будет зависеть в этих слоях от координаты х. На рис. 6.5 сплошная линия 1 показывает распределение напряженности поля в статическом режиме (или когда переменное поле проходит через нулевое значение), а пунктирные линии соответствуют максимальным 2 и минимальным 3 значениям результирующей напряженности поля, наступающим при амплитудных значениях синусоидальной напряженности поля E(t).
Возможность усиления в ЛПД объясним с помощью пространственно-временной диаграммы (рис. 6.6).
 Рис. 6.6
Рис. 6.6
Напряженность синусоидального во времени поля E(t) существует во всем пространстве от х=0 до x=ω, но на рисунке она изображена при х=xл, соответствующем началу слоя дрейфа. Позже будет объяснено, что при большой амплитуде напряженности поля лавинный процесс приводит к образованию короткого сгустка носителей, запаздывающего на четверть периода от максимума поля. Этому сгустку соответствует короткий импульс лавинного тока iл(t) на границе х=xл между слоями умножения и дрейфа. Далее носители сгустка двигаются в электрическом поле слоя дрейфа, пока на достигнут его гратгцы x=ω при угле пролета θдр. Пространственно-временная диаграмма для слоя дрейфа изображена на 7.6 прямыми литиями, так как дрейфовая скорость носителей постоянна.
Угол пролета при выбранной ширине слоя ω зависит от частоты. Если θдр<π, ςо носители все время пролета находятся в тормозящем полупериоде поля и отдают свою энергию полю, вызывая его увеличение. При θдр>π οоследнюю часть пути в области дрейфа носители летят в ускоряющем полупериоде поля, что ослабляет эффект предыдущего взаимодействия и приводит в целом к снижению энергии, передаваемой носителями полю за все время пролета. Если θдр=2π, ςо эффект взаимодействия носителей и поля исчезает.
На рис. 6.6 при х=ω показана зависимость дрейфового тока от времени iдр(t) в виде узкого импульса, повторяющего импульс iл(t). Изображена также кривая наведенного тока iнав(t), созданного движением короткого сгустка на пути от х=xл до x=ω. В случае короткого сгустка форма кривой наведенного iнав(t) созданного движением короткого сгустка на пути от х=xл тока близка к прямоугольной. Разложением в ряд Фурье может быть определена первая гармоника iнав(1) этого тока. В идеальном случае она находится в противофазе с полем, если θдр=π. Οо амплитуде первой гармоники наведенного тока и амплитуде поля можно найти мощность, передаваемую потоком носителей электрическому нолю.
Ток проводимости в слое умножения. Систему уравнений непрерывности для слоя умножения можно записать в виде
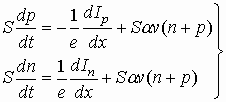 (6.12)
(6.12)
где v—скорость электронов и дырок (для упрощения приняты равными); S—площадь сечения структуры.
Левая часть каждого уравнения есть изменение числа носители в слое длиной 1 см и сечением S за 1с. Первые слагаемые в правой части учитывают изменение числа носителей за 1 с вследствие прохождения тока. Вторые слагаемые показывают, сколько пар носителей в рассматриваемом объеме образуется за 1 с электронами (Sαvn) и дырками (Sαvp). В (6.12) не учтена рекомбинация носителей в слое умножения, так как обычно время пролета носителей в этом слое много меньше времени жизни.
В слое умножения ток вызван дрейфовым движением носителей. При пренебрежении диффузией носителей дырочная и электронная составляющие тока
Ip = Sеvр, In = Sеvn, (6.13)
а весь ток
I = Ip+In = Sеv(n+p). (6.14)
При большой напряженности поля, характерной для лавинного пробоя, скорость носителей равна так называемой скорое, насыщения—максимально возможной скорости носителей в полупроводниках (vн = 107 см/с). Поэтому время пролета носителей слоя лавинного умножения
![]() (6.15)
(6.15)
Из (6.13) следует, что
![]()
![]()
Подставляя эти величины в (6.12) и учитывая (6.14), получим
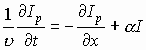
![]()
Складывая эти уравнения, получим
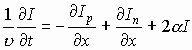 (6.16)
(6.16)
Для решения (6.16) принимается допущение, что полный ток I равный сумме Ip и In, не зависит от координаты х, как в статическом режиме. Тогда I(х) = const. а вместо частной производной dI /dt можно записать dI/dt.
Умножим (6.16) на dx и проинтегрируем по координате x от 0 до xл:
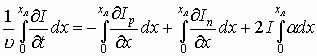
Это уравнение с учетом (6.15) приводится к виду
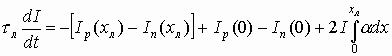 (6.17)
(6.17)
Вычислим разности токов, входящие в правую часть (6.17), Полный ток в сечении х=xл I=Ip(xл)+In(xл), поэтому
![]() (6.18)
(6.18)
Полный ток в сечении х=0 I=Ip(0)+In(0). Подставляя эту разность в (6.17), получим
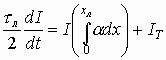 (6.19)
(6.19)
где
Iт=Ip(0)+In(xл) (6.20)
Очевидно, что Ip(0)=Iр0, где Iр0 — ток, создаваемый дырками, приходящими в слой умножения слева из n-области, а In(0)=In0, где In0 — ток, создаваемый электронами, входящими в слой умножения справа. Таким образом, (6.20) определяет тепловой ток перехода Iт, (или ток насыщения), которым при большом коэффициенте лавинного умножения можно пренебречь.
Токи в слое умножения при малой амплитуде поля. Обычно вводят среднее значение коэффициента ионизации по слою умножения
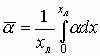 (6.21)
(6.21)
Тогда вместо (6.19) можно написать
![]() (6.22)
(6.22)
Пренебрегая в последнем уравнении Iт получаем
![]() (6.23)
(6.23)
Используем (6.23) для определения переменного тока, появляющегося при приложении к диоду переменного напряжения. Рассмотрим режим, когда амплитуда переменной составляющей напряженности поля Ел в слое умножения много меньше постоянной составляющей (режим малых амплитуд). Постоянную составляющую примем равной критическому, значению Екр, удовлетворяющему условию лавинного пробоя (6.11). Тогда мгновенное значение напряженности поля
![]() ,
, ![]() (6.24)
(6.24)
Максимальные и минимальные значения Е в структуре показаны на рис. 6.5
Будем также предполагать в режиме малых амплитуд изменения коэффициента ионизации α и тока I малыми, т. е.
![]() ,
, ![]() (6.25)
(6.25)
![]() ,
, ![]() (6.26)
(6.26)
где — комплексные амплитуды соответствующих величин. В первом приближении можно записать
![]() (6.27)
(6.27)
Используя (6.25) и (6.27), получаем
![]() (6.28)
(6.28)
Определим величину ![]() , входящую в(6.23). На основании (6.28)
, входящую в(6.23). На основании (6.28)
![]()
По условию пробоя (6.11) и (6.21) ![]() = 1 поэтому
= 1 поэтому
![]() (6.29)
(6.29)
Подставляя (6.26) и (6.29) в (6.23) и пренебрегая членами второго порядка малости, получаем
![]() (6.30)
(6.30)
Если ширина слоя умножения xл сравнительно небольшая, то мал и переменный заряд в этом слое. Поэтому напряженность переменного поля практически одинаковая по всему слою, так что падение напряженности на слое умножения
Uл=Eлxл (6.31)
Используя (6.30) и (6.31), получаем
Iл=Uл/iωLл (6.32)
где
Lл=τл/2I0α’ (6.33)
эквивалентна индуктивности, так как ток отстает от напряжения на 90°, и названа индуктивностью лавины.
Полученный результат является следствием инерционности процесса образования лавины носителей. Когда поле пройдет максимальное значение и начнет уменьшаться, концентрация носителей еще продолжает возрастать. Максимумы концентрации носителей и тока в линейной теории достигаются к моменту времени, когда переменная составляющая поля, уменьшаясь, проходит через нулевое значение (отставание по фазе на 90°, рис. 6.7).
 Рис. 6.7
Рис. 6.7
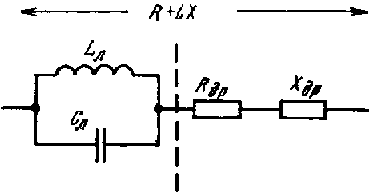 Рис. 6.8
Рис. 6.8
С увеличением переменного напряжения на слое умножена Uл (рис. 6.7, а) предположение о малости сигнала перестанет вы подняться. Изменение тока во времени будет все сильнее отличаться от синусоидального закона (6.26) и начнет приобретав импульсный характер. Как показывает специальное решение (6.23), положение максимума импульса тока (пунктир на рис. 6.7, б) практически совпадает с максимальным значением тока при слабом сигнале. Поэтому слой умножения приближенно можно рассматривать как источник импульсов тока, запаздывающих по отношению к максимальному значению напряжения на четверть периода.
Ток смещения в слое умножения с учетом (6.24) и (6.31)
![]() (6.34)
(6.34)
где
![]() (6.35)
(6.35)
эквивалентная емкость слоя умножения, а S — площадь сечения.
Полный ток слоя равен сумме тока проводимости (6.32) и тока смещения (6.34), но последний при пренебрежении влиянием переменного заряда совпадает с емкостным током. Поэтому
![]() (6.36)
(6.36)
Соответственно полная проводимость слоя умножения
![]() (6.37)
(6.37)
Эквивалентная схема слоя умножения при малой амплитуде поля. В соответствии с (6.37) слой умножения может быть представлен эквивалентной схемой — параллельным колебательным контуром, содержащим индуктивность Lл ,и емкость Сл (рис. 6.8). Полное сопротивление слоя из (6.37)
![]() (6.38)
(6.38)
где
![]() (6.39)
(6.39)
— собственная резонансная частота контура, называемая лавинной частотой. С учетом (6.15), (6.33) и (6.35)
![]() (6.40)
(6.40)
где i0=I0/S — плотность тока, а vн—скорость насыщения.
Лавинная частота fл пропорциональна корню 'квадратному из плотности тока и производной от коэффициента ионизации по напряженности поля α'.
Токи в слое дрейфа при малой амплитуде поля. Рассмотрим теперь составляющие полного тока слоя дрейфа и его полное сопротивление. В этом слое постоянная составляющая напряженности поля меньше критического значения Екр, но достаточно велика, чтобы скорость носителей оставалась практически равной скорости насыщения vн. При постоянстве скорости ток проводимости в любом сечении х в момент временя t равен тому току, который был в начале слоя дрейфа в более ранний момент временя t – τx, где τx — время пролета от начала слоя до данного сечения. Для удобства рассмотрения поместим начало координат на границе слоев умножения и дрейфа, тогда τx=x/vн. Теперь в области дрейфа ток проводимости
Iдр (x,t)= I0 (0,t – τx) (6.41)
где I0(0,t – τx) – ток проводимости в начале слоя дрейфа (x=0),
в момент времени t – τx можно определить по (6.26). Переменная составляющая тока проводимости
![]() (6.42)
(6.42)
Определим наведенный ток, создаваемый переменным зарядом в слое дрейфа в момент времени t.
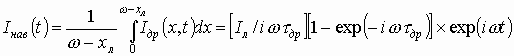 (6.43)
(6.43)
где
![]() (6.44)
(6.44)
— время пролета в слое дрейфа.
Комплексная амплитуда наведенного тока в (6.43)
![]() (6.45)
(6.45)
Емкостный ток слоя дрейфа
![]() (6.46)
(6.46)
где емкость слоя дрейфа
![]() (6.47)
(6.47)
С учетом (6.45) и (6.46) полный ток
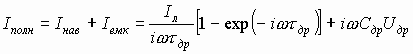 (6.48)
(6.48)
Из (6.36) можно найти связь Iл с полным током
![]() (6.49)
(6.49)
Следовательно, из (6.48) можно записать полное сопротивление слоя дрейфа
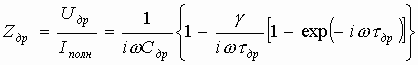 (6.50)
(6.50)
Эквивалентная схема слоя дрейфа при малой амплитуде поля. После преобразований (6.50) сводится к виду
![]() (6.51)
(6.51)
где активное сопротивление дрейфового слоя
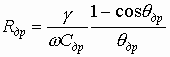 (6.52)
(6.52)
реактивное сопротивление дрейфового слоя
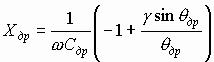 (6.53)
(6.53)
В (6.52) и (6.53) использовано обозначение для угла пролета
![]() (6.54)
(6.54)
Эквивалентная схема слоя дрейфа показана на рис. 6.8.
Рис. 6.9 Рис. 6.10
Из (6.52) следует, что активное сопротивление слоя отрицательно на всех частотах ω>ωл (γ<0), κроме частот, на которых Rдр=0 (при θдр=2πn, n=1, 2,....). Зависимость Rдр от угла пролета θдр показана на рис. 6.9. Максимум отрицательного сопротивления наблюдается вблизи θдр=π. При дальнейшем увеличении θдр до 2π, Rдр уменьшается до нуля.
Таким образом, диапазон частот, в котором может быть обеспечено отрицательное сопротивление, велик. Однако, обычно считают, что ЛПД хорошо работает лишь на частотах, соответствующих углу пролета θдр=ωτдр=π. Θз этого условия с учетом (7.44) для узкого слоя умножения (xл<<ω) можно определять пролетную частоту
fпр = ωпр/2π = 1/2τдр = vн/2ω. (6.55)
Если ω = 5 мкм и vн ≈107 м/с, то fпр=20 ГГц.
Эквивалентная схема ЛПД в пролетном режиме работы для малого сигнала показана на рис. 6.8. Контур LлСл характеризует процессы в слое умножения, а Rдр и Хдр — процессы в слое дрейфа. Полное сопротивление ЛПД Z=R+iX. Примерная зависимость активного R и реактивного Х сопротивлений от частоты показана на рис. 6.10. На частотах ниже лавинной fл активное сопротивление ЛПД положительное, а реактивное имеет индуктивный характер. На частотах выше fл активное сопротивление отрицательное, а реактивное становится емкостным. Наличие отрицательного сопротивления и позволяет использовать ЛПД для создания генераторов и усилителей СВЧ.
6.3. Параметры и характеристики генераторов и усилителей на ЛПД в пролетном режиме
Режимы генерации и усиления. На основе ЛПД можно создать СВЧ генераторы (ГЛПД) и усилители (УЛПД). В обоих случаях ЛПД включен в колебательную систему. Генерацию или усиление объясняют наличием при определенном режиме работа ЛПД отрицательного сопротивления R (см. pис. 6.10).
Отрицательное сопротивление зависит от тока ЛПД, поэтов в ГЛПД с заданным сопротивлением потерь (сопротивления нагрузки, резонатора и областей диода) существует минимальный пусковой ток, начиная с которого возможна генерация. При токе менее пускового обеспечивается усилительный режим. Простейшая схема ГЛПД показала на рис. 6.11. Схема содержит коаксиальный резонатор 1, перестраиваемый с помощью поршня 2 (плунжера), и ЛПД, помещенного между центральным проводником резонатора и его торцом (ЛПД находится в пучности напряжения).
Простейшим вариантом УЛПД является регенеративный усилитель отражательного типа (рис. 6.12). Источник сигнала и нагрузка включены в два плеча волноводного циркулятора. К третьему плечу присоединена колебательная система с ЛПД. Усиление сигнала происходят в результате его взаимодействия с колебательной системой, имеющей отрицательную добротность, и может рассматриваться как поступление в нагрузку через циркулятор отраженного усиленного сигнала.
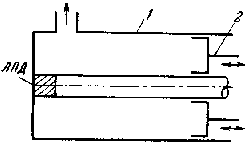
Рис. 6.11
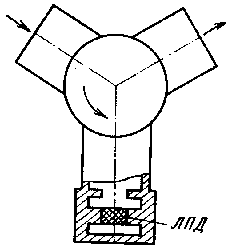
Рис. 6.12
Выходная мощность и электронный КПД ГЛПД. Будем считать, что напряжение на ЛПД синусоидальной, импульсы лавинного тока короткие и сдвинуты относительно максимумов СВЧ напряжения на четверть периода (см. рис. 6.7б), а угол пролета в слое дрейфа оптимальный (180°), как показано на рис. 6.6. В этом случае импульсы наведенного тока гнав практически можно считать прямоугольными с длительностью, равной полупериоду. Если I0 — среднее значение наведенного тока, то амплитуда импульсов наведенного тока составит примерно 2I0, а амплитуда его первой гармоники при разложении в ряд Фурье
I1 ≈ 4I0/π.
Мощность СВЧ колебаний в дрейфовом слое
P=0.5 I1Uдр1(6.56)
гае Uдр1 — амплитуда синусоидального напряжения на слое дрейфа. Для грубой оценки обычно считают, что Uдр1 не превышает половины постоянного напряжения U0 на диоде (Uдр1 ≈ U0/2), чтобы мгновенное напряжение на диоде не стало прямым (положительным). Тогда из (6.56) P ≈ I0U0/π = P0/π, ΰ электронный КПД
ηэ=P/P0≈1/π (6.67)
составит примерно 30%, что весьма близко к лучшим экспериментальным результатам, полученным для ЛПД из арсенида галлия.
Выходная мощность не может превышать потребляемой. Поэтому обычно для оценки максимальной выходной мощности определяют максимальную потребляемую диодом мощность Р0mах, где U0mах и I0mах — максимальное допустимое напряжение на диоде и соответствующий ему максимальный ток.
Очевидно, что самое большое значение U0mах будет в том случае, когда по всей длине перехода w поле будет одинаковым и равным критическому, т. е. U0mах = Eкрw. По теореме Гаусса заряд в переходе q=εSEкр, а максимальный ток при времени пролета τдр=w/vн составит I0mах = q/τдр = εSEкрvн/w. Следовательно,
Р0mах = εSvнЕ2кр (6.58)
Обычно это условие записывают в ином виде, вводя емкостное сопротивление прибора Хс = l/ωC=w/ωεS. С учетом этого (7.58) приводится к виду
Р0mах f2= v2нЕ2кр/8πXc. (6.59)
Условие (7.59) означает, что при постоянном емкостном сопротивлении прибора Xc потребляемая мощность обратно пропорциональна квадрату частоты:
Р0mах f2 = const. (6.60)
На более низких частотах ограничение связано не с процессами в переходе, а с теплоотводом, и вместо (7.60) получено условие
Р0mах f = const. (6.61)
На рис. 6.13 показаны расчетные зависимости мощности от частоты, соответствующие (6.60) и (6.61).
Ограничение полезной мощности связано также с влиянием объемного заряда при больших плотностях тока, необходимых для получения значительной мощности. Учет объемного заряда приводит к тому, что перед движущимся электронным сгустком поле увеличивается, а за ним уменьшается по сравнению с полем, котoрoе было до появления электронов. Снижение поля за сгустком вызовет уменьшение коэффициентов умножения, а следовательно и лавинного тока, который пройдет через максимальное значение ранее, чем показано на рис. 6.6. С ростом объемного заряда отставание импульса тока от СВЧ напряжения уменьшается. Последнее приведет к уменьшению амплитуды СВЧ колебаний, так как образовавшийся сгусток, войдя в слой дрейфа, некоторое время двигается в ускоряющем поле и отбирает энергию от СВЧ поля. Кроме того, чем больше исходный ток I0, тем меньший коэффициент лавинного умножения требуется для получения заданного лавинного тока и меньшее время необходимо для достижения максимума лавинного тока. Это также уменьшает запаздывание лавинного тока относительно максимума переменного напряжения.
Рис. 6.13
У самых высокочастотных ЛПД с малой шириной обедненной области w для получения ударной ионизации необходима напряженность поля Е>106 В/см. Однако при таком поле уже возможен туннельный пробой. Появляющийся туннельный ток синфазен с переменным напряжением, поэтому исчезает запаздывание, необходимое для получения отрицательного сопротивления. Кроме того, при Е>106 В/см коэффициенты ионизации слабо зависят от поля. Это приводит к расширению лавинного импульса, изменению формы наведенного тока уменьшению полезной мощности и КПД.
Шумы. Уровень шумов в ЛПД в основном определяется флуктуациями лавинного тока, выходящего из слоя умножения. Эти флуктуации объясняются, во-первых, статистическим разбросом моментов поступления неосновных носителей в слой умножения, а во-вторых, флуктуацией числа частиц в лавинах, образованных каждым пришедшим носителем заряда. Флуктуации, связанные с первой причиной, подобны дробовому шуму и растут с увеличением тока. Исследования показывают, что флуктуации тока, вызванные второй причиной, значительно больше дробовых флуктуации исходного тока и растут с увеличением среднего числа носителей в лавине. При приближении к лавинной частоте уровень шума резко возрастает. Установлено также, что шум возрастает при увеличении амплитуды СВЧ напряжения или выходной мощности.
Расчетно и экспериментально найдено, что в пролетном режиме работы минимальные шумы у ЛПД из арсенида галлия, а максимальные — у ЛПД из кремния. Меньший коэффициент шума в случае, арсенида галлия объясняют равенством коэффициентов ионизации электронов и дырок (αn=αp). Коэффициент, шума ЛПД по сравнению с другими полупроводниковыми и электровакуумными, приборами высок, что является существенным недостатком. Минимальный коэффициент шума усилителей на ЛПД составляет около 20дБ.
6.4. Особенности устройства и применения ЛПД
Для изготовления ЛПД используют кремний, германий и арсенид галлия. Требуемую структуру получают методами эпитаксиального наращивания, диффузии и ионного легирования.
Для создания ЛПД миллиметрового диапазона применяют метод ионного легирования — получение необходимого закона распределения примесей бомбардировкой полупроводника ионами, ускоренными до высокой энергии (десятки-сотни килоэлектронвольт). Этот метод позволяет легко контролировать закон распределения и концентрацию примеси и создавать очень узкие переходы (десятые доли микрометра). При этом появляется возможность получения при очень узких переходах так называемых двухпролетных ЛПД миллиметрового диапазона. Одновременное использование эффекта пролета электронов и дырок возникающих в общем слое умножения, приводит к росту выходной мощности и КПД примерно в 2 раза.
В непрерывном режиме мощность ЛПД в трехсантиметровом диапазоне составляет 1—3,5 Вт при КПД до 20%, а в двухсантиметровом 1—2,5 Вт при КПД до 17%. В лабораторном образце достигнута мощность 5 Вт на частоте 12,4 ГГц при КПД 20%. В импульсном режиме при λ=3 см получены мощность от 15 до 50 Вт и КПД 10%, на частотах 33—36 ГГц соответственно 5 Вт и 7%, а в диапазоне 93—96 ГГц 1 Вт и 5%.
В последнее время ЛПД широко применяются для создания СВЧ усилителей. Диод является активным двухполюсником, т. е. двухполюсником с отрицательным дифференциальным (динамическим) сопротивлением. Поэтому в усилителе применяется циркулятор, обеспечивающий разделение входного и выходного сигналов (см. рис. 6.12).
В пролетном режиме ЛПД отрицательное сопротивление существует в широкой области рабочих частот. Поэтому частоту генерации в генераторах на ЛПД можно изменять в пределах более октавы механической перестройкой колебательной системы. Широко используют также электрическую перестройку частоты, включая в колебательную систему СВЧ варикап или ферритовые элементы. В первом случае диапазон перестройки обычно невелик, а во втором — достигает 10%. Температурный коэффициент частоты генератора зависит от изменения как параметров диода, так и колебательной системы. Для одноконтурного генератора ТКЧ ≈ ±104 1/0С может быть снижен в результате принятия специальных мер.
Высокий уровень шума ЛПД позволяет использовать их для создания генераторов шума СВЧ диапазона. Эти генераторы очень просты, имеют большую спектральную плотность мощности шума, низкую потребляемую мощность, малые массу и габариты, т. е. выгодно отличаются от электровакуумных генераторов шума.
Усилители на ЛПД вследствие значительного коэффициента шума (20-30 дБ) не используются во входных усилителях. По коэффициенту преобразования амплитудной модуляции в фазовую (АМ/ФМ) усилители на ЛПД сравниваются с лампами бегущей волны. Так, для кремниевого ЛПД на частоте примерно 11 ГГц при выходной мощности около 0,5 Вт этот коэффициент 3.5 град/дБ.
В заключение, следует отметить существование аномального режима ЛПД— режима с захваченной плазмой или ткаррат — режима (сокращение от слов ТРApped Plasma Avalanche Triggered Trarbit — захваченная плазма, пробег области лавинного умножения). В электронно-дырочном переходе в этом режиме создаются условия для движения фронта лавинного умножения со скоростью в несколько раз большей максимальной скорости носителей (скорости насыщения, см. рис. 6.1). Поэтому в переходе очень быстро образуется электронно-дырочная плазма, что приводит к резкому снижению напряжения на переходе, следовательно, к уменьшению скорости электронов и- дырок в плазме (захваченная плазма). Увеличение времени пролета носителей в переходе вызывает снижение частоты генерации в несколько раз по сравнению с пролетным режимом работы ЛПД. Однако достоинством ЛПД с захваченной плазмой является снижение потребляемой мощности, вследствие понижения напряжения на диоде после возникновения плазмы; КПД в этих приборах увеличивается (30—50%). В импульсном режиме на частоте 3,2 ГГц получена мощность 150 Вт и КПД 21%, а на частоте 1,1 ГГц при пяти последовательно включенных диодах — 1,2 кВт и КПД около 26%. В непрерывном режиме работы мощность ЛПД с захваченной плазмой не превышает 5—10 Вт.
Контрольные вопросы.
- Принцип действия и структура лавинно-пролетных диодов.
- Объясните процесс лавинного нарастания тока в ЛПД и его тормажение высокочастотным полем.
- Основные параметры генераторов на ЛПД.
- Характеристики генераторов и усилителей на ЛПД.
- Применение ЛПД.
7. Эффект Ганна и приборы на его основе
7.1. Диод Ганна
Диод Ганна представляет собой полупроводниковый кристалл с двумя омическими контактами для внешних выводов (рис. 7.1, а). В качестве полупроводникового материала используется арсенид галлия GaAs или другой материал, в которых проявляется эффект Ганна (см. ниже) . Полупроводник имеет донорную примесь с концентрацией n =1014 ¸ 1016 1/см3. Так как полупроводники, в которых проявляется эффект Ганна, при контакте с металлами обычно образуют барьер Шоттки, то для организации нормального омического контакта формируются дополнительные слои n+ с концентрацией 1018 - 1019 1/см3 (рис. 7.1, б). Активная часть диода Ганна (n- слой) имеет длину 1¸ 100 мкм, диаметр 50¸ 250 мкм и более.
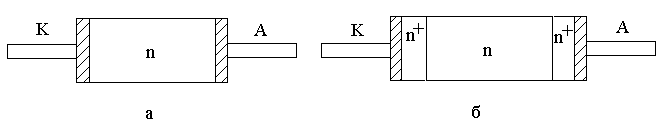 Рис. 7.1
Рис. 7.1
Омические контакты с соответствующими выводами называются, как и у остальных диодов, катодом и анодом, но принципиально они не имеют особого различия.
При работе катод соединяется с отрицательным, а анод с положительным выводом источника питания. Так как основная масса зарядов - это электроны, то при наличии тока на анодном выводе выделяется тепловая энергия и поэтому вывод анода должен иметь хороший теплоотвод. По этой причине он выполняется более массивным и обычно соединяется с корпусом устройства.
7.2. Эффект Ганна
Для некоторых полупроводников (например, арсенид галлия GaAs, фосфид индия InP и др.) энергетическая диаграмма в зоне проводимости имеет сложную структуру. Если изобразить зависимость энергии электрона от волнового вектора, то для указанных выше полупроводников имеются один основной и один или несколько побочных минимумов в зоне проводимости (рис. 7.2). Благодаря этому электроны в зоне проводимости могут находиться в различных энергетических состояниях - либо в основном минимуме (долине), или в побочном, отстоящем для GaAs от основного примерно на величину D W = 0,36 эВ. Таким образом зона проводимости как бы состоит из нескольких подзон. Электроны, находящиеся в нижней подзоне, имеют меньшую энергию (“холодные” электроны), а в верхней подзоне - большую (“горячие” электроны).
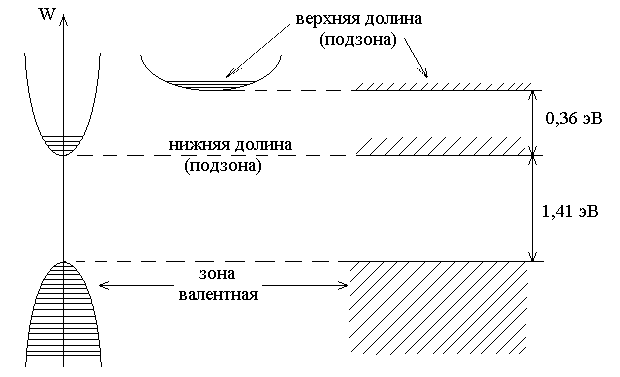
Рис. 7.2
На движение электронов, а также на их энергетическое состояние влияет как внешнее электрическое поле Е0, создаваемое источником питания, так и внутреннее кристаллическое поле.
Для оценки суммарного влияния внутреннего и внешнего электрических полей вводится понятие эффективной массы электронов. В нижней долине (основном минимуме) m1эфф = 007 m0 (“легкие”, но “холодные” электроны), а в верхней (боковом минимуме) m2эфф = 1,2 m0 (“тяжелые”, но “горячие” электроны), где m0 - масса свободного электрона. Подвижности электронов также резко отличаются. Для “холодных” электронов m 1=5000 см2/В*с, а для “горячих” - m 2=100 см2/В*с.
Обозначим концентрацию “легких” электронов n1 , а “тяжелых” n2; тогда n0 = n1 + n2 . При слабом внешнем электрическом поле почти все электроны зоны проводимости находятся в нижней подзоне, то есть n2=0, n1= n0. Дрейфовая скорость электронов Vдр 1 = m 1*Е , то есть изменяется линейно с ростом Е (рис. 7.3, а).
Плотность тока: J = e (m 1*n1+m 2*n 2)E = e*m 1*n0*E=e*n0*Vдр 1, то есть так же растет линейно с ростом напряженности поля (рис. 6.3,б).
При возрастании внешнего поля до величины Е > Е1 (для арсенида галлия Е1 = 3*103 В/см, для фосфида индия Е1 = 6*103 В/см) одновременно с некоторым увеличением скорости электронов начинают сказываться различные эффекты, связанные со столкновениями электронов с узлами кристаллической решетки, из-за чего повышается температура электронного “газа” и электроны получают возможность перейти в верхнюю долину. При значении внешнего поля Е ³ E2 (обычно E2 » 2E1) практически все электроны окажутся в верхней долине (n1» 0 ). Дрейфовая скорость электронов соответственно равна: V др 2 = m 2 Е, а плотность тока - J = e m 2 n2 E = e m 2 n0 E = e n0 Vдр 2 .
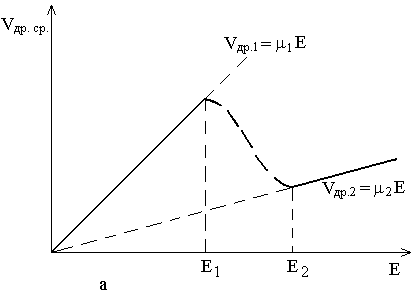
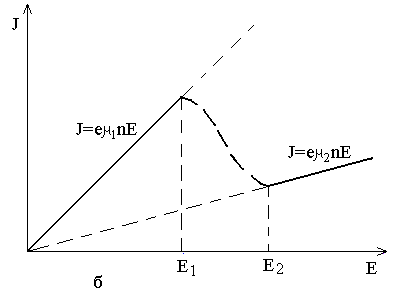
Рис. 7.3
Совершенно очевидно, что на участке E1< E< E2 должны наблюдаться уменьшение средней дрейфовой скорости и спад плотности тока при росте напряженности внешнего поля (отрицательная дифференциальная подвижность и отрицательное дифференциальное сопротивление) (рис. 7.3, а, б).
Следует отметить, что такой вид графиков будет наблюдаться, если переход электронов из нижней энергетической подзоны в верхнюю будет происходить одновременно по всему объему полупроводника.
Экспериментальное исследование образцов из указанных выше полупроводников с примесью n - типа показало, что интенсивный междолинный переход электронов происходит не по всему объему образца, а в некоторых областях, в первую очередь там, где имеются неоднородности. Даже в химически однородных образцах из-за наличия омических контактов (анода и катода - рис. 7.4) будут возникать области с повышенными значениями напряженности поля, и, следовательно, вблизи контактов в первую очередь возникает междолинный переход электронов.
Из-за малого времени взаимодействия электронов с полем неоднородность вблизи анодного контакта практически не влияет на процессы в образце и ниже мы будем учитывать влияние неоднородности только вблизи катода.
Итак, при увеличении электрического поля именно вблизи катода (рис. 7.4, а, б, в) создаются благоприятные условия для перехода электронов в верхнюю подзону (долину) с одновременным резким уменьшением дрейфовой скорости. Переход некоторого количества электронов в верхнюю подзону приведет к увеличению сопротивления этого участка образца, что в свою очередь ведет к дальнейшему увеличению электрического поля на этом участке и уменьшению поля слева и справа от участка. Увеличение поля на “горячем участке” ведет к увеличению числа “горячих” электронов.
Независимо от того, являются ли электроны “горячими” или “холодными”, все они движутся к аноду. При движении к аноду в участок с “горячими”, но медленными электронами будут вливаться слева догоняющие их быстрые электроны, увеличивая концентрацию электронов на “горячем участке”. А “холодные” электроны, двигавшиеся справа от слоя горячих, быстро уходят в отрыв, обеспечивая преобладание положительных зарядов кристалла (донорных ионов) непосредственно перед слоем “горячих” электронов (рис. 7.4, г).
Таким образом, движение “горячих” и “холодных” электронов приводит к формированию подвижного двойного электрического слоя зарядов - домена.
Появление двойного электрического слоя дополнительно увеличивает напряженность поля в доменной области и еще более способствует переходу электронов в верхнюю долину.
Этот процесс продолжается до тех пор, пока с одной стороны, практически все электроны в этой области не станут “горячими”, а с другой - произойдет выравнивание дрейфовых скоростей электронов, движущихся в составе домена и вне его (Vдр 1= m Е1= Vдр 2= m 2 Е2 ). Выравнивание происходит за счет значительного ослабления электрического поля за пределами домена. После выравнивания скоростей концентрация электронов, а также дрейфовая скорость не изменяются, то есть формирование домена закончилось. Время формирования домена t ф = 10-12 ¸ 10-13 с.
Ток в цепи полупроводникового образца в течении всего времени движения домена от катода к аноду остается практически постоянным. При достижении анода домен рассасывается, общее сопротивление образца уменьшается и ток возрастает, однако рассасывание домена у анода создает возможность для формирования нового домена у катода и процесс повторяется. В результате ток через образец будет претерпевать периодические изменения (рис. 7.4) с частотой:
![]() ; где: l - длина образца, Vдр - средняя дрейфовая скорость, f пр - пролетная частота.
; где: l - длина образца, Vдр - средняя дрейфовая скорость, f пр - пролетная частота.
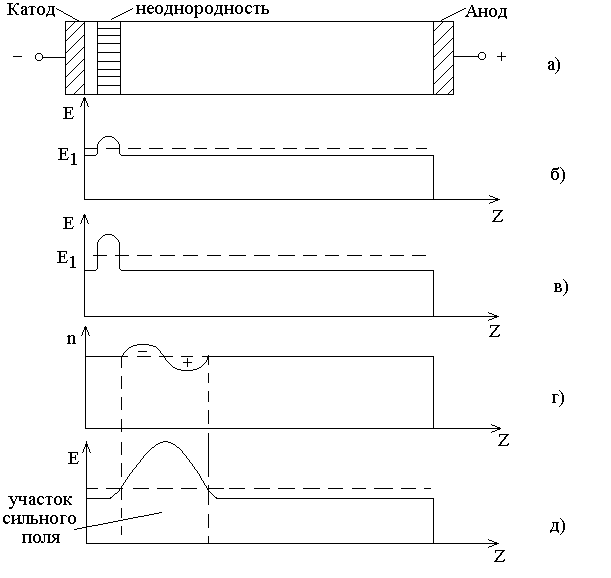
Рис. 7.4
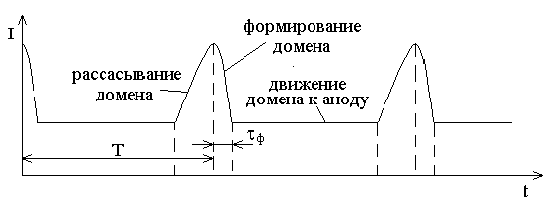
Рис. 7.5
Разумеется все эти процессы протекают при условии, что внешняя цепь полупроводникового образца не влияет на законы изменения тока, в частности, источник питания не стабилизирован по току.
Обобщая вышесказанное, можно сделать следующие выводы:
а) участки образца вне домена ведут себя как обычная среда, проводимость которой подчиняется закону Ома;
б) участок образца внутри домена обладает отрицательным дифференциальным сопротивлением, что позволяет использовать образцы в качестве активных элементов усилителей и генераторов СВЧ.
Для реального диода при работе в динамическом режиме зависимость Vдр.ср. от напряжения и ВАХ (рис. 7.6) отличаются от идеализированных (рис. 7.3, а, б).
В динамическом режиме и Vдр.ср., и ток через образец при U > Uп уменьшаются, а затем остаются практически постоянным. Это объясняется тем, что резкое увеличение поля наблюдается только в относительно узкой полоске образца, а за пределами домена поле остается относительно слабым. При этом рост напряжения приводит к расширению участка с сильным полем, а участки со слабым полем слева и справа от домена соответственно уменьшаются. Электрическое поле и скорость движения электронов на участках вне домена остаются неизменными.
При значительном увеличении приложенного напряжения температура кристалла увеличивается, что может привести к перегреву (прожиганию) кристалла.
Аналогичный вид будет иметь график зависимости Vдр. ср.= F(U) (рис. 7.6, б).
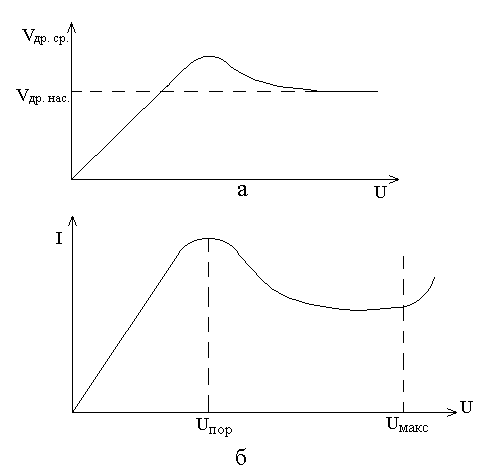
Рис. 7.6
7.3. Влияние внешней цепи
Выше предлагалось, что внешняя цепь состоит только из источника питания и соединительных проводов, представляющих собой чисто активные (омические) элементы. В действительности на СВЧ как элементы внешней цепи (обычно это колебательная система), так и элементы самого диода Ганна будут иметь реактивные сопротивления и поэтому внешняя цепь вместе с диодом будет представлять довольно сложную колебательную систему с определенными резонансными частотами. Возбуждение на этих частотах неминуемо приведет к тому, что диод Ганна окажется под воздействием не только постоянного, но и переменного напряжений (и, соответственно, полей), что может существенно повлиять на физические процессы в диоде Ганна.
При достаточно большой амплитуде колебаний во время положительного полупериода могут возникнуть условия для формирования домена, а при отрицательном - для рассасывания домена или задержки его образования. Таким образом, внешняя цепь существенно влияет на режим работы диодов Ганна.
7.4. Режимы работы диодов Ганна
В зависимости от амплитуды колебаний, а также от соотношения времени пролета домена и периода колебаний возможны следующие режимы работы диодов Ганна.
Пролетный режим.
Этот режим полностью соответствует описанному выше эффекту Ганна. Он возможен при работе диода на колебательную систему с низкой добротностью. При этом U~ << U0, а генерируемая частота приблизительно равна пролетной частоте:
![]() , то есть генерируемая частота определяется геометрическими размерами образца. Так как Vдр.нас.=107 см/сек, то
, то есть генерируемая частота определяется геометрическими размерами образца. Так как Vдр.нас.=107 см/сек, то ![]() .
.
График изменения тока (см. рис. 7.5) во внешней цепи имеет явно выраженный несинусоидальный характер, амплитуда первой гармоники тока при такой форме импульсов относительно невелика, поэтому этот режим характерен низким КПД (не более 10%, чаще всего 2 ¸ 5%).
Режим с задержкой образования домена.
Этот режим реализуется при использовании колебательной системы с невысокой и средней добротностью и частотой настройки f < f пр. Для объяснения этого режима на рис. 7.7 показаны временные диаграммы напряжения и тока диода.
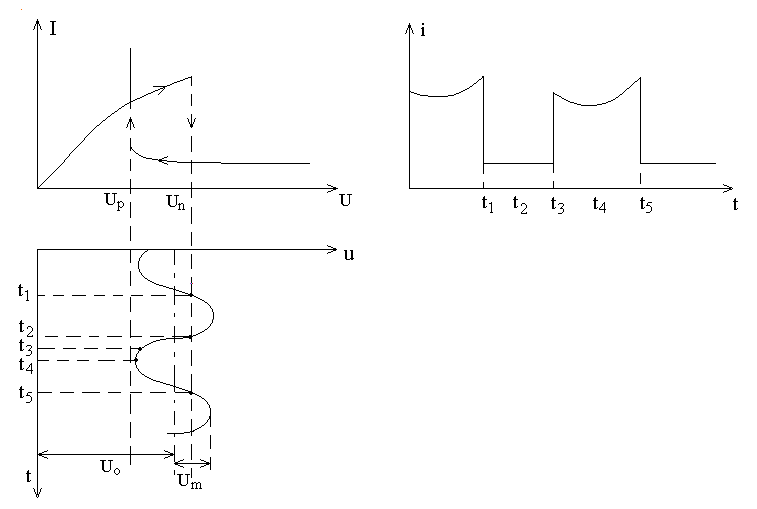 Рис. 7.7 Введем обозначения: U0 - постоянное напряжение, приложенное к диоду Ганна; Um- амплитуда переменного напряжения; Uп- пороговое напряжение, при котором возникает домен; Uр- напряжение, при котором рассасывается домен;
Рис. 7.7 Введем обозначения: U0 - постоянное напряжение, приложенное к диоду Ганна; Um- амплитуда переменного напряжения; Uп- пороговое напряжение, при котором возникает домен; Uр- напряжение, при котором рассасывается домен;
Uп >Uр, так как до образования домена поле внутри “горячего” участка создается в основном внешним напряжением, а когда домен сформирован львиная доля электрического поля в горячем участке создается доменом и домен будет еще существовать даже при уменьшении внешнего напряжения ниже порогового.
Для этого режима U0 - Um>Uр, то-есть после возникновения домен может исчезнуть только при достижении анодного контакта. В момент t1 U ³ Uп и, следовательно, домен образуется и начинает двигаться к аноду. Ток в этот момент падает до минимального значения и остается практически постоянным в течение всего времени движения домена. Рассасывание домена происходит при достижении доменом анодного контакта (предположим, это момент t3 ).
Отрицательное дифференциальное сопротивление диода будет обеспечиваться, если момент прихода домена на анод и, следовательно, момент рассасывания домена лежит в пределах t2 - t4. Это объясняется тем, что с одной стороны в момент рассасывания напряжение должно быть меньше порогового, а с другой - напряжение в момент рассасывания домена должно уменьшаться. Так как при рассасывании домена ток увеличивается, то диод Ганна в этот момент представляет собой устройство с отрицательным дифференциальным сопротивлением. После рассасывания домена новый домен образуется не сразу, а в момент t5, когда U ³ Uп. В этот момент диод также ведет себя как устройство с отрицательным сопротивлением, так как напряжение увеличивается, а ток при образовании домена уменьшается.
В этом режиме время движения домена должно быть меньше периода колебаний. Обычно Т/2 £ t £ Т, или 0,5 fпр £ fраб £ fпр .Форма импульсов тока в этом режиме близка к прямоугольной, что обеспечивает наибольшую амплитуду первой гармоники и, следовательно, повышенное значение КПД (до 27%).
Режим с подавлением (гашением) домена.
В этом режиме в течение части периода U0- Um< Uр и поэтому домен может расформировываться (рассасываться), не доходя до анода. В момент t1 (U ³ Uп) домен возникает и существует до времени t2, когда U = Uр (рис. 7.8). Время пролета домена от катода до анода должно быть больше той части периода, когда напряжение меняется от Uп до Uр (t > t2 - t1), то-есть домен еще не доходит до анода, когда напряжение уменьшается до Uр.
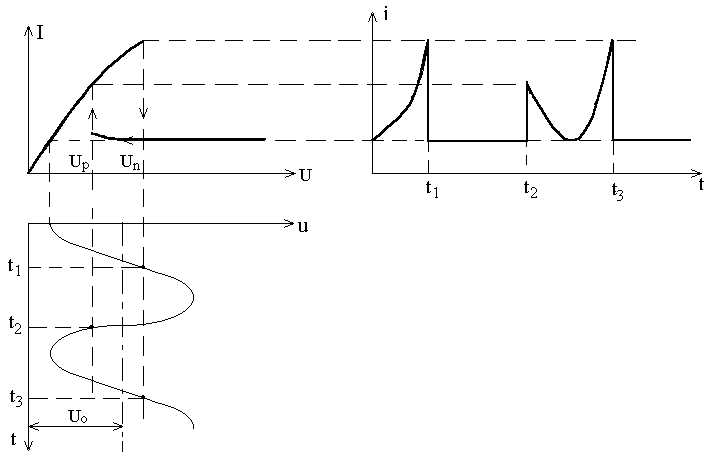 Рис. 7.8
Рис. 7.8
Новый домен возникает в момент t3 и далее процесс повторяется. Рабочая частота в этом случае может изменяться в пределах:
0,75 f пр £ f раб £ (2 ¸ 3)f пр.
КПД генератора при работе в этом режиме меньше, чем в режиме с задержкой образования домена, но больше, чем в пролетном. Обычно КПД составляет 8 ¸ 12 %.
Режим с ограниченным накоплением объемного заряда (ОНОЗ).
Этот режим возможен при настройке высокодобротной колебательной системы на частоту, много больше пролетной (fраб >> fпр). При большой добротности системы амплитуда колебаний достигает значительной величины и во время отрицательного полупериода при U< Uп (промежуток t 1), происходит рассасывание накопленного заряда (рис. 7.3).
При достаточно высокой частоте колебаний домен не успевает сформироваться, однако ток через образец периодически изменяется, уменьшаясь при увеличении U свыше Un и увеличиваясь при уменьшении U ниже Un.
Таким образом, и в этом режиме диод Ганна ведет себя как устройство с отрицательным сопротивлением.
Для обеспечения режима ОНОЗ необходимо обеспечить условия, при которых формирование домена было бы затруднено. Это обеспечивается технологически путем максимального исключения возможных неоднородностей, то есть использования сверхчистых однородных кристаллов.
Ограничение накопления объемного заряда позволяет использовать для этого режима образцы с большим пролетным промежутком, а также использовать повышенные рабочие напряжения, что ведет к увеличению выходной мощности устройств. Однако серьезной проблемой остается обеспечение высокой добротности колебательной системы, а также высокой однородности кристалла.
Гибридные режимы.
Эти режимы характеризуются тем, что в различные части периода могут существовать различные режимы (сначала доменный, а потом ОНОЗ).
Независимо от типа режима, во всех случаях диод Ганна представляет собой устройство с отрицательным дифференциальным сопротивлением и может быть использован для создания генераторов и регенеративных усилителей СВЧ диапазона.
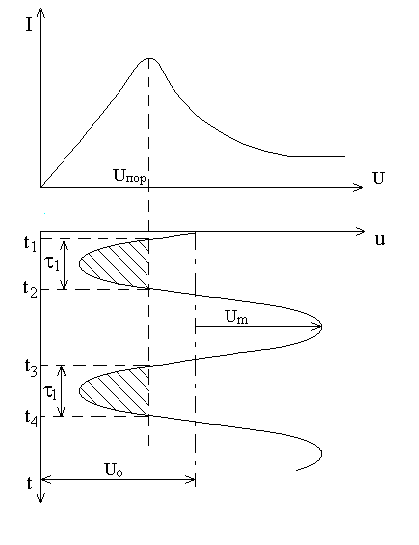
Рис. 7.9
7.5. Конструктивное оформление и основные параметры диодов Ганна
Любые СВЧ диоды, в том числе и диоды Ганна, могут иметь патронную, таблеточную, волноводную, коаксиальную, полосковую и прочие варианты конструкций, в том числе бескорпусную [3, 4, 6] . Кроме этого диоды Ганна могут быть сформированы в кристаллической подложке полупроводниковых ИМС.
В настоящее время промышленностью выпускаются различные типы диодов Ганна, предназначенные для усиления и генерации на частотах от 1 ¸ 2 ГГц до 150 ГГц и более. При этом отдельный тип диодов способен работать в диапазоне частот не более 20 - 30% от средней частоты. Выходные мощности в непрерывном режиме от единиц милливатт в верхней части СВЧ диапазона до единиц ватт в дециметровом и метровом диапазоне. Повышенные значения выходной мощности для всех режимов, кроме ОНОЗ, получают путем увеличение рабочего тока диода, что в свою очередь требует увеличения площади поперечного сечения кристалла и улучшения теплоотвода.
Для частот ниже 1 ГГц диоды Ганна не выпускаются, так как для работы на этих частотах промышленность освоила выпуск СВЧ транзисторов с хорошими показателями и гораздо лучшими функциональными возможностями.
7.6. Эквивалентные схемы генераторов на диодах Ганна
Генератор на диоде Ганна представляет собой колебательную систему (резонатор) с установленным в ней диодом Ганна. Эквивалентная схема генератора должна включать эквивалентные схемы диода, колебательной системы и нагрузки.
Диод Ганна может быть представлен обычной эквивалентной схемой СВЧ диода (рис. 7.10, а). На этой схеме последовательное сопротивление r, индуктивность выводов L и емкость корпуса Ск зависят от конструкции элементов структуры и ее свойств, а отрицательное активное сопротивление диода - R и емкость Сд зависят еще и от режима питания диода.
При известных параметрах эквивалентной схемы диода и частоте эта схема может быть пересчитана в простую двухэлементную последовательную цепочку (рис. 7.10, б) или параллельную цепочку (рис. 7.10, в).
Эквивалентная схема генератора может быть представлена в двух вариантах - в виде последовательной эквивалентной схемы или параллельной.
В последовательной эквивалентной схеме (рис. 7.11, а):
-Rд , Xд - элементы эквивалентной схемы диода Ганна (рис. 7.10, б);
L, C, R - элементы колебательной системы;
R¢ н - эквивалентное (с учетом связи) сопротивление нагрузки.
Генерация возможна, если |-Rд | ³ R + R¢ н
В параллельной эквивалентной схеме (рис. 7.11, б):
-Gд, Вд - элементы эквивалентной схемы диода Ганна (рис. 7.10, в);
L, C, G - элементы колебательной системы;
G¢ н - эквивалентная проводимость нагрузки.
Генерация возможна, если |-Gд | ³ G + G¢ н.
Приведенные эквивалентные схемы являются упрощенными и могут использоваться для частот не свыше 10 ¸ 11 ГГц.
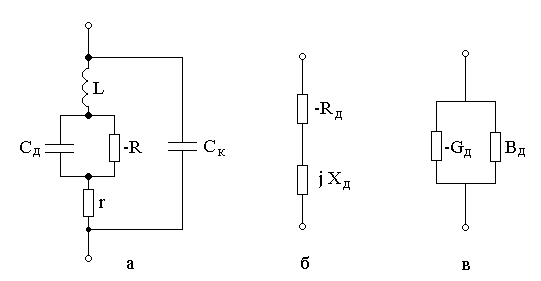
Рис. 7.10
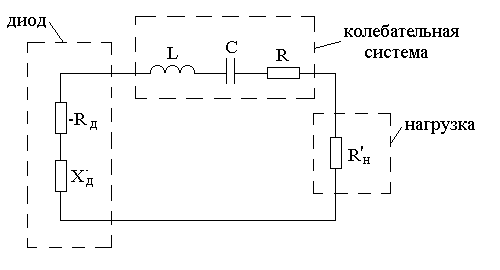
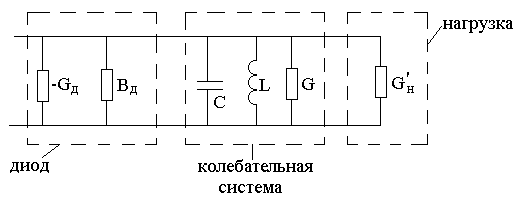
Рис. 7.11
Контрольные вопросы.
- Объяснить эффект Ганна на основе двухдолинной модели энергетических состояний полупроводника.
- Пояснить возникновение и исчезновений домена в полупроводниках.
- Пояснить устройство диода Ганна.
- Объяснить работу диодов Ганна в различных режимах.
- Эквивалентная схема диода Ганна и ее элементы.
- Конструктивные особенности диодов Ганна различных типов.
- Основные области применения диодов.
- Пояснить устройство генераторов на диодах Ганна.
- Пояснить методы перестройки частоты генераторов.
8. Физические основы квантовых приборов
8.1. Энергетические уровни
Квантовая система, состоящая из микрочастиц, электронов, ядер, атомов и так далее, отличаются тем, что ее внутренняя энергия может принимать только дискретные значения. Возможные дискретные значения энергии называют энергетическими уровнями.
В свободных атомах квантуется энергия электронов и имеется система энергетических уровней электронов. Наблюдаются следующие движения частиц: движение электронов в атоме, колебания атомов в молекуле, вращение и поступательное движение молекул. Квантование энергии приводит к образованию сложной системы энергетических уровней. Основной системой являются электронные уровни ЭУ, отстоящие друг друга на 1 – 10 эВ. Между электронными уровнями располагаются колебательные уровни КУ с расстоянием примерно 0,1 эВ, а между колебательными уровнями находятся вращательные уровни ВУ с интервалом 10ֿ³ эВ и менее.
Переходы между электронными уровнями соответствуют излучению в видимом и ультрафиолетовом диапазонах, между колебательными уровнями - инфракрасному, а между вращательными - СВЧ диапазону.
В твёрдых телах взаимодействие частиц становится настолько сильным, что образуются зоны с очень близко расположенными уровнями, между этими зонами имеются зоны запрещённых значений энергии (запрещённые зоны).
В атомах осуществляются только те переходы между энергетическими уровнями, которые удовлетворяют правилам отбора, устанавливающим допустимые различия квантовых чисел. Переходы, удовлетворяющие правила отбора, называются разрешёнными, а остальные - запрещёнными. Переходы с излучением или поглощением квантов электромагнитной энергии (фотонов) называют излучательными, а переходы, в которых квант энергии выделяется в виде тепла в среде,- безызлучательными. Состояние, из которого запрещены все излучательные переходы в более низкие энергитические состояния, называется метастабильными.
8.2. Квантовые переходы
Спонтанные переходы – самопроизвольные квантовые переходы из верхнего энергетического состояния в нижнее. Уровень, соответствующий наименьшей возможной энергии, называется основным, а остальные – возбуждёнными. Частота излучения определяется из постулата Бора
![]() ,
,
где энергия верхнего (εj ) и нижнего (εi ) уровней; h- постоянная Планка. Частота ![]() называется частотой квантового перехода. Число частиц с одинаковой энергией в единице объёма называется населённостью уровня. Пусть номер верхнего уровня j=2, а нижнего i=1. Обозначим населённости этих уровней N2 и N1. При спонтанных переходах происходят изменение населённости уровней, уменьшение верхнего 2 и увеличение нижнего 1.
называется частотой квантового перехода. Число частиц с одинаковой энергией в единице объёма называется населённостью уровня. Пусть номер верхнего уровня j=2, а нижнего i=1. Обозначим населённости этих уровней N2 и N1. При спонтанных переходах происходят изменение населённости уровней, уменьшение верхнего 2 и увеличение нижнего 1.
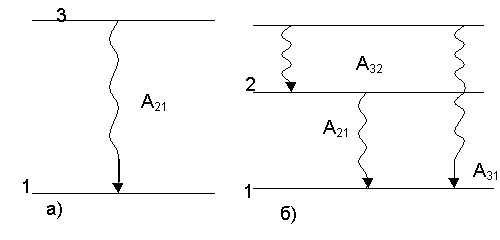
Рис. 8.2
Уменьшение населённости уровня 2 в результате только спонтанных переходов за время dt пропорционально населённости этого уровня N2 и времени dt: dN2= -A21N2dt, где A21_- коэффициент Эйнштейна для спонтанных переходов, определяющий вероятность спонтанного перехода в 1 с. Решив, получить экспоненциальный закон уменьшения населённости уровня 2 во времени:
N2(t)=N2(0)exp(A21t),
где N2(0) – населённость в момент времени t = 0.
Насколько уменьшится населённость N2 настолько же возрастёт населённость N1 так как общее число частиц в объёме остаётся неизменным. Из этого следует, что через время t=1/A21 населённость N2 уменьшится в е = 2,718 раза по сравнению с начальным значением N2(0). Величина τ²=1/A21 характеризует время жизни в возбуждённом состоянии 2 и называется временем жизни на уровне. Коэффициент Эйнштейна объёма в 1с, или среднее число частиц, совершивших самопроизвольный переход из верхнего состояния в нижнее, т. е. имеет размерность и может быть любым, в отличии от математической вероятности, меняющейся от 0 до 1.
За 1 с в единице объёма число спонтанных переходов
N21(c)=A21N2.
При каждом спонтанном переходе частицы выделяется квант энергии, поэтому за 1 с с учётом излучается энергия
P21(c)=n21(c)hν21=A21N2hν21.
Случайность спонтанных переходов означает, что различные частицы излучают неодновременно и независимо, т. е., фазы электромагнитных волн, излучаемых отдельными частицами, не согласованы друг с другом. Излучение обычных источников света есть результат спонтанных переходов.
В системе частиц, имеющих несколько энергетических уровней возможны спонтанные переходы частиц с данного уровня на нижние. Полная вероятность Ај спонтанного перехода с уровня ј на все нижние уровни ί πавна сумме вероятностей отдельных переходов А јί:
A ј= Σ A јі = A ј1+Aј2+...+A ј(ј-1).
Уровни, для которых вероятность спонтанных переходов очень мала, называют метастабильными.
Время жизни на уровне j в многоуровневой системе определяется аналогично с учётом.
τ j=1/A j.
Вынужденные переходы – это квантовые переходы частиц под действием внешнего электромагнитного поля, частота которого совпадает или близка к частоте перехода. При этом возможны переходы с верхнего уровня 2 на нижний 1 и с нижнего на верхний. В первом случае под действием внешнего электромагнитного поля с частотой ν21 происходит вынужденное испускание кванта энергии hν21. Особенность вынужденного испускания состоит в том, что появившийся фотон полностью идентичен фотону внешнего поля. Вынужденное излучение имеет такие же частоту, фазу, направление распространения и поляризацию, как и вынуждающее излучение. Поэтому вынужденное излучение увеличивает энергию электромагнитного поля с частотой перехода ν21. Это служит предпосылкой для создания квантовых усилителей и генераторов.
В противоположность этому для перевода частицы из нижнего энергетического состояния 1 в верхнее 2 необходимо затратить энергию внешнего поля, равную разности энергии верхнего и нижнего уровней.
Таким образом, при каждом вынужденном переходе снизу вверх затрачивается квант энергии внешнего поля hν21.
Вынужденные переходы, так же как и спонтанные, имеют статистический характер. Поэтому вводится вероятностные коэффициенты: W21 - вероятность вынужденного перехода сверху вниз и W12 - снизу вверх в 1с. Эти вероятности определяются соотношениями,
W21=B21uν, W12=B12uν,
где В21 и В12 - коэффициенты Эйнштейна для вынужденных переходов с излучением и поглощением энергии соответственно.
Число вынужденных переходов сверху вниз с излучением энергии в единицу времени в единицу объёма пропорционально вероятности W21 и населённости верхнего уровня N2.
n21(в)=W21N2=B21uνN2.
Аналогично при тех же условиях число вынужденных переходов снизу вверх с поглощением энергии:
n12(в)=W12N1=B12uνN1
Соотношение между коэффициентами Эйнштейна.
Связь между коэффициентами Эйнштейна А21, В21 и В21 можно установить, предполагая, что внутри полости, представляющей абсолютно чёрное тело, находится система атомов при температуре Т.
Пусть система атомов имеет два уровня энергии ε2 и ε1 , при переходах между которыми излучается или поглощается квант энергии hν21. При термодинамическом равновесии в системе не происходит изменения энергии, поэтому число излучённых квантов должно быть равно числу поглощённых.
Следовательно, в единицу времени во всей системе общее число переходов из верхнего энергетического состояния в нижнее должно быть равно общему числу переходов из нижнего в верхнее:
n21=n12.
В состоянии равновесия в системе имеется равновесная плотность поля излучения uν, которая определяет число вынужденных переходов в системе.
Полное число переходов сверху вниз n21в состоянии равновесия определяется суммой числа спонтанных переходов n21(с) и вынужденных переходов с излучением энергии n21(в),
n21=n21(с)+n21(в)=(A21+B21uν)N2.
Число переходов n12 снизу вверх определяется только вынужденными переходами с поглощением.
n12=n12(в)=B12uνN1.
Приравнивая на основании n21 и n12 получаем
B12uνΝ1=(A21+B21uν)N2
Из этого найдём равновесную плотность энергии поля
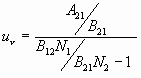
Соотношение населенностей уровней в состоянии термодинамического равновесия определяется законом Больцмана.
N2б/N1б=(g2/g1)exp[-(ε2-ε1)/κΤ],
где g1 и g2 -статистический вес уровней; κ - постоянная Больцмана; Т- абсолютная температура.
Для невырожденных уровней (g¹=g²=1) закон Больцмана принимает более простую форму записи
N2б/N1б=exp[-(ε2-ε1)/κΤ],
которая будет далее использоваться. Учитывая, что ε2 - ε1 = hν21, получаем
![]()
Эйнштейн постулировал, что равновесная спектральная плотность энергии поля должна быть равна её значению, рассчитанному по формуле Планка для равновесного излучения абсолютно чёрного тела:
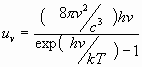
если вместо hν подставить hν21.
Сравнивая с учётом этого, получаем условия тождественности этих формул:
B12=B21,
A21=(8πhν³21/c³)B21.
Таким образом, если квантовая система и поле излучения находятся в состоянии термодинамического равновесия, то вероятности вынужденных переходов в единицу времени при единичной плотности полей В12и В21 должны быть одинаковы. Вероятность спонтанных переходов пропорциональна третьей степени частоты перехода, поэтому спонтанное излучение сильнее всего проявляется в оптическом диапазоне волн.
Безызлучательные переходы. Атомы и молекулы газа в результате неупругих соударений друг с другом или с электронами теряют или приобретают энергию. При этом энергия электромагнитного поля не излучается, не поглощается. Такие энергетические переходы принято называть безызлучательными. В твёрдом теле безызлучательные переходы происходят вследствие колебательного движения кристаллической решетки.
Безызлучательные переходы характеризуются также вероятностью перехода между уровнями j и i сверху вниз ωјі и снизу вверх ωіј соответственно с потерей и получением порции энергии
В соответствии с принципами детального равновесия в состоянии термодинамического равновесия подобно число безызлучательных переходов с уровня ј на уровень і в 1 с равно числу обратных безызлучательных переходов с уровня і на уровень ј:
ωјіΝј=ωіјΝі.
В состоянии термодинамического равновесия распределение населённостей определяется законом Больцмана.
ωјі/ωіј = exp (hνјі/κΤ),
Из чего следует, что вероятность безызлучательных переходов сверху вниз больше, чем снизу вверх, т.е. ωјі>ωіј ј>і, в отличие от вероятностей вынужденных переходов, которые одинаковы ( Wji = Wij). Если hνјі<<κΤ, что обычно справедливо для квантовых приборов СВЧ диапазона, то можно заменить выражением
ωјі/ωіј=1+hνјі/κΤ.
Релаксационные переходы. Изолированная система, в которой распределение частиц по энергии отличается от равновесного, называется неравновесной. Неравновесное состояние наблюдается при внешнем воздействии, после прекращения которого система возвращается в равновесное состояние. Процесс установления равновесия в системе называется релаксацией, а переходы частиц с одного уровня на другой в процессе релаксации - релаксационными переходами. В основе процесса релаксации лежит взаимодействие частиц (электронов, атомов, молекул, ионов) между собой и со стенками объёма. Рассмотренные безызлучательные переходы являются релаксационными. К релаксационным переходам следует отнести и спонтанные, роль которых в оптическом диапазоне. Рекласационные переходы приходится учитывать при рассмотрении процессов, выводящих систему из равновесного состояния. При постоянном внешнем воздействии возможна компенсация релаксационных процессов, тогда система будет находится в стационарном неравновесном состоянии. Релаксационные переходы влияют также на ширину спектральной линии.
8.3. Ширина спектральной линии
Естественная ширина спектральной линии. До сих пор предполагалось, что энергетические уровни бесконечно узкие. Однако даже в идеализированном случае, когда на частицу не действуют внешние силы, ширина энергетических уровней кончена. Другими словами, изучение для данного перехода не монохроматическое, а имеет некоторый спектр частот. Зависимость интенсивности излучения от частоты называют спектральной линией излучения, а графическое изображение её – контуром спектральной линии.
Минимальная ширина уровней, а, следовательно, и минимальная ширина спектральной линии определяется соотношением неопределённостей Гейзенберга, которое в данном случае лучше записать в виде
∆ε ∆t≥h
где ∆ε и ∆t - неопределённости энергии и времени.
Предположим, что необходимо определить частоту излучения при переходе с уровня 2 на основной уровень 1. Время жизни частиц в возбуждённом состоянии определяется τ2=1/A21. Следует считать, что неопределённость времени равна времени жизни частиц, т.е. Δt=τ2. Подставляя Δt, получаем неопределённость энергии уровня 2 Δε2>h/τ2. Неопределённость энергии любого уровня j
Δ εј>h/τј,
где τј – время жизни частицы на уровне ј, определяемое по вероятностям спонтанных переходов с него на нижние уровни.
Соотношение определяет зависимость ширины любого энергетического уровня от среднего времени жизни частиц на этом уровне. Если последнее бесконечно велико, то неопределённость энергии, или ширина уровня, бесконечно мала.
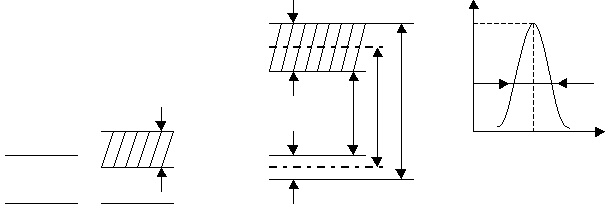
Рис. 8.3
Такими будут основной энергетический уровень, нижний уровень системы. Наиболее широкими оказываются уровни с малым временем жизни. Неопределённость частоты перехода между “размытыми” уровнями и с ширинами и находятся из соотношения и определяется суммой неопределённостей энергии обоих уровней. Ширина спектральной линии изолированного и неподвижного атома, определяемая только временем жизни естественной шириной спектральной линии. Ширину контура спектральной линии принято определять как разность частот, на которых интенсивность равна половине максимального значения. Частотой перехода называют частоту, соответствуюшую максимуму спектральной линии. Форма спектральной линии может быть представлена так называемой лоренцевой кривой совпадающей с резонансной кривой колебательного контура. Реальные наблюдаемые спектральные линии имеют ширину больше естественной.
Уширение спектральной линии из-за столкновений. В газе происходят упругие и неупругие столкновения частиц. При упругих столкновениях суммарная кинетическая энергия сталкивающихся частиц не изменяется: частицы не обмениваются внутренней энергией и не переходят на другие энергетические уровни. При неупругих столкновениях суммарная кинетическая энергия сталкивающихся частиц либо возрастает, либо убывает. В этом случае изменяется внутренняя энергия сталкивающихся частиц, связанная с электронными, колебательными и вращательными уровнями.
В результате неупругих столкновений происходит сокращение времени жизни рассматриваемых частиц в данном энергетическом состоянии до времени среднего пробега между двумя столкновениями, что эквивалентно увеличению ширины спектральной линии.
Вероятность столкновений частиц, следовательно, вероятность квантовых переходов одинаковы для частиц газа. Поэтому форма и ширина спектральной линии всего газа и каждой частицы одинаковы, при этом ширина линии газа и частиц стала больше естественной спектральной линии. Такой процесс называют уширением спектральной линии.
Однородное уширение наблюдается также в случае столкновения частиц газа со стенками, ограничивающими объём газа. Влияние этих столкновений на ширину спектральной линии становится основным при малом давлении газа, когда вероятность столкновений частиц мала.
Доплеровское уширение спектральной линии. Это уширение связано с эффектом Доплера, т. е. с зависимостью наблюдаемой частоты излучения от скорости движения излучателя. Если источник, создающий в неподвижном состоянии монохроматическое излучение с частотой, движется со скоростью в сторону к наблюдателю так, что проэкция скорости на направление наблюдения составляет, то наблюдатель регистрирует более высокую частоту излучения.
![]()
где с - фазовая скорость распространения волны; 0 - угол между направлениями скорости излучателя и наблюдения.
В квантовых системах источниками излучения являются атомы или молекулы. В газообразной среде при термодинамическом равновесии скорости частиц распределены по закону Максвелла- Больцмана. Поэтому и форма спектральной линии всего вещества – будет связана с этим распределением. В спектре, регистрируемом наблюдателем, должен быть непрерывный набор частиц, так как разные атомы движутся с разными скоростями относительно наблюдателя. Учитывая лишь проекции скорости в распределении Максвелла- Больцмана, можно получить следующее выражение для формы доплеровской спектральной линии:
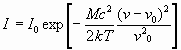
Эта зависимость является гауссовой функцией. Соответствующая значению ширина линии.
![]()
С увеличением массы частиц М и понижением температуры Т ширина линии уменьшается.
Вследствие эффекта Доплера спектральная линия всего вещества не совпадает со спектральной линией отдельной частицы. Наблюдаемая спектральная линия вещества представляет собой суперпозицию спектральных линий всех частиц вещества, т. е. линий с различными центральными частотами. Для лёгких частиц при обычной температуре ширина доплеровской линии в оптическом диапазоне может превышать естественную ширину линии на несколько порядков и достигать значения более1ГГц.
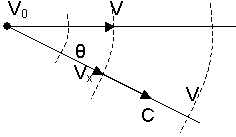
Процесс, при котором форма спектральной линии всего вещества не совпадает с формой спектральной линии каждой частицы, называют неоднородным уширением спектральной линии. В рассмотренном случае причиной неоднородного уширения был эффект Доплера. Форма доплеровской спектральной линии описывается гауссовой функцией. Если распределение скоростей частиц отличается от максвелловского, то и форма доплеровской спектральной линии будет отличаться от гауссовой функции, но уширение останется неоднородным.
Другие причины уширения спектральной линии. В квантовых приборах широко используют твёрдые вещества с примесными ионами, квантовые переходы которых являются рабочими. Колебания кристаллической решетки модулируют электрическое поле в том месте, где находится ион, и, следовательно, модулируют положение его энергетических уровней и увеличивает ширину спектральной линии. Кроме того, ширина линии увеличивается вследствие тепловых колебаний самих ионов. Причиной уширения спектральной линии твёрдого тела может быть пространственная неоднородность физических параметров среды или неоднородности электрического и магнитного полей. Эти неоднородности будут вызывать неоднородное уширение спектральной линии. Причиной уширения может быть также электромагнитное излучение, вызывающее вынужденные переходы между рассматриваемыми уровнями и приводящее к изменению времени жизни частицы. Поэтому, например, процесс генерации излучения в квантовых приборах будут приводить к изменению ширины линии
Спектральные коэффициенты Эйнштейна. Введённые ранее коэффициенты Эйнштейна определяют мощность, излучаемую или поглощаемую во всём спектральном диапазоне данного перехода между ними. Поэтому их называют интегральными коэффициентами Эйнштейна. Если их необходимо учитывать частотное распределение излучаемой или поглощаемой мощности, то используют спектральные коэффициенты Эйнштейна aji, bji, bij, которые связаны с Аji, Вji и Вij соотношениями
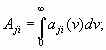
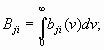
Частотная зависимость всех спектральных коэффициентов одинакова и совпадает с формой контура спектральной линии данного перехода – лоренцевой или гауссовой кривыми. Однако с введением коэффициентов а, и следует уточнить также понятие населённости уровней. Под населённостью любого уровня следует понимать частиц в единице объёма, энергия которых попадает в пределы размытости уровня по энергии. Таким образом, число спонтанных и вынужденных переходов в единичном частном интервале вблизи частоты в единицу времени можно записать с использованием дифференциальных коэффициентов Эйнштейна в виде.
8.4. Возможность усиления и генерации в квантовых системах
Возможность усиления и генерации в квантовых приборах связана с наличием вынужденного излучения в среде, на которую воздействует электромагнитное поле. Однако при этом происходят вынужденные переходы с поглощением энергии и релаксационные переходы. Вынужденные переходы с излучением и поглощением энергии имеют резонансный характер, так как происходят при совпадении частоты поля с частотой квантового перехода, точнее, когда частота поля находятся в пределах спектральной линии вещества.
Рассмотрим обмен энергии между полем и веществом. Будем предполагать, что вещество имеет два энергетических уровня с населённостями N1 и N2, а частота внешнего поля равна частоте квантового перехода v21 . При объёмной плотности энергии число вынужденных переходов в единицу времени в единицу объёма с выделением энергии с учётом
n12 = BuvN2,
а выделяемая при этих переходах энергия в единице объёма в единицу времени, т. е. мощность,
Pвыд = n21hv21 = BuvN2hv21.
Аналогично число вынужденных переходов с поглощением энергии и поглощаемая от внешнего поля мощность в единице объёма соответственно равны:
n12 = BuvN1
Pпогл = n12hv21 = BuvN1hv21
С учётом изменение мощности электромагнитного поля. Назовём эту величину мощностью взаимодействия. P = Pвыд - Pпогл
Если Р>0, т. е. выделяемая мощность превышает поглощаемую, то в системе происходит увеличение энергии поля, или усиление электромагнитного поля. При Р<0 преобладает поглащение энергии энергия внешнего поля убывает.
В обычном состоянии термодинамического равновесия населенность верхнего уровня меньше, чем нижнего N2<N1, в соответствии с законом Больцмана. Поэтому вещество в этом состоянии поглощает энергию внешнего поля (Р < 0), так как число квантовых переходов снизу вверх (1→2) с поглощением энергии больше числа квантовых переходов сверху вниз (2→1) с выделением энергии.
Соотношение N2>N1 является обратным по отношению к состоянию термодинамического равновесия, когда N2<N1. Поэтому состояние, при котором N2>N1, т. е. возможно усиление, называют состоянием с инверсией населённостей уровней.
Закон Больцмана справедливый только для термодинамического равновесия, можно записать
![]()
Величину Тп называют температурой перехода. В состоянии термодинамического равновесия N1>N2, т.е. Тп>0. Если формально воспользоваться N2>N1, то получится отрицательная температура перехода
Тп<0. Только в состоянии термодинамического равновесия температура перехода совпадёт с истинной температурой вещества Т. Условия усиления N2>N1 эквивалентно отрицательной температуре перехода Тп<0. Поэтому состояние с инверсией населённостей уровней иногда называют состоянием с отрицательной температурой, а неравенство Тп<0 - условием усиления в квантовых системах. Среда, в которой имеется состояние с инверсией населённостей, называется также активной средой, так как в ней возможно усиление электрического поля.
8.5. Взаимодействие бегущих электромагнитных волн с активной средой
Предположим, что электромагнитная волна падает на активную среду и распространяется в ней в виде плоской волны по направлению оси. Пусть S - поток энергии через единичное поперечное сечение – изменяется при прохождении излучения через вещество, так как в нём происходят вынужденные переходы с выделением и поглощением энергии. Изменения в слое за 1 с, т. е. изменение мощности.
Рис. 8.4
Поток энергии связан с объёмной плотностью энергии и групповой скоростью соотношением.
Исключая uv , получаем:
![]()
![]()
или
![]()
где![]() , χ- коэффициентом поглощения. Сначала будем считать, что объемная плотность энергии в веществе на столько мала, что можно пренебречь изменением населенности уровней N1 и N2. Тогда (N1- N2) не зависит от координаты z, т.е. не зависит от z коэффициент χ и интегрирование приводит к формуле:
, χ- коэффициентом поглощения. Сначала будем считать, что объемная плотность энергии в веществе на столько мала, что можно пренебречь изменением населенности уровней N1 и N2. Тогда (N1- N2) не зависит от координаты z, т.е. не зависит от z коэффициент χ и интегрирование приводит к формуле:
S(z)=S(0)exp(-χz),
где S(0)- плотность потока энергии в начале образца (z = 0).
Полученная формула называется интегральным законом Бугера.
Из уравнения коэффициента поглощения следует, что при N1>N2 (нет инверсии населенностей) и закон описывает поглощение энергии внешнего поля в веществе, а χ имеет смысл коэффициента (показателя) поглощения, показывающего, на кокой длинне энергия волны убывает в е = 2,72 раза.
При N2>N1 (инверсия населенностей) χ<0, поэтому отражает усиление поля в веществе. В этом случае говорят об отрицательном коэффициенте поглощения или вводят понятие показатель усиления активной среды:
χ а = - χ = Bhυ(N2-N1)/υг.
Тогда закон Бугера можно записать
S(z)=S(0)exp (χaz)
Проведенное рассмотрение не учитывало потерь энергии в среде, пропорциональных проходящей мощности S. Будем считать, что эти потери распределены равномерно по координате z. Тогда дифференциальный закон Бугера можно записать в более общем виде:
dS(z)/dz=[χа (υ0)-α]S(z)
Потери в активной среде ослабляют усилительный эффект и вызывают ограничение проходящей мощности. С учетом потерь интегральный закон Бугера выглядит так:
S(z)=S(0) exp (χa-α)z
При увеличении проходящей мощности необходимо учитывать зависимость χа от z. При небольших потерях в активной среде χа=α переходит в χа. В этом случае предельная мощность получается практически при наступлении насыщения перехода. Впред не зависит от входной мощности S(0). На рисунке показана зависимость S(z) при различных значениях S(0):
Контрольные вопросы.
- Виды квантовых переходов. Правило Бора.
- Понятие о населенностях уровней. Закон Больцмана.
- Вынужденные переходы частиц между уровнями. Излучательные и безызлучательные переходы. Вероятность перехода и их число.
- Закон Бугера. Возможность усиления электромагнитных волн веществом. Инверсия населенности уровней.
9. Лазеры
Лазером называют генератор электромагнитного излучения оптического диапазона, основанный на использовании вынужденного излучения. В лазерах используется вещество, в котором в процессе накачки может быть создана активная лазерная среда, обладающая способностью усиления электромагнитного излучения на частоте квантового перехода. В зависимости от агрегатного состояния лазерного вещества различают газовые, твердотельные, полупрозрачные и жидкостные. Система накачки лазера должна обеспечивать передачу энергии от внешних источников питания к активному веществу для создания инверсии населенностей уровней. Положительная обратная связь в лазере создаётся с помощью оптического резонатора 1.
Полупроводниковые лазеры отличаются от газовых и твердотельных тем, что излучающие переходы происходят в полупроводниковом материале не между дискретными энергетическими состояниями электрона, а между парой широких энергетических зон. Поэтому переход электрона из зоны проводимости в валентную зону с последующей рекомбинацией приводит к излучению, лежащему в относительно широком спектральном интервале и составляющему несколько десятков нанометров, что намного шире полосы излучения газовых или твердотельных лазеров.
9.1. Создание инверсной населенности в полупроводниках
Рассмотрим собственный полупроводник. В условиях термодинамического равновесия валентная зона полупроводника полностью заполнена электронами, а зона проводимости пуста. Предположим, что на полупроводник падает поток квантов электромагнитного излучения, энергия которых превышает ширину запрещенной зоны hv>Eg. Падающее излучение поглощается в веществе, так как образуются электронно-дырочные пары. Одновременно с процессом образования электронно-дырочных пар протекает процесс их рекомбинации, сопровождающийся образованием кванта электромагнитного излучения. Согласно правилу Стокса - Люммля энергия излученного кванта меньше по сравнению с энергией генерирующего кванта. Разница между этими энергиями преобразуется в энергию колебательного движения атомов кристаллической решетки. В условиях термодинамического равновесия вероятность перехода с поглощением фотона (валентная зона - зона проводимости) равна вероятности излучательного перехода (зона проводимости - валентная зона).
Предположим, что в результате какого-то внешнего воздействия полупроводник выведен из состояния термодинамического равновесия, причем в нем созданы одновременно высокие концентрации электронов в зоне проводимости и дырок в валентной зоне. Электроны переходят в состояние с некоторой энергией Fn вблизи потолка валентной зоны. Рассматриваемая ситуация иллюстрируется диаграммами, приведенными на рис. 9.1. Так как все состояния вблизи дна зоны проводимости заполнены электронами, а все состояния с энергиями вблизи потолка валентной зоны заполнены дырками, то переходы с поглощением фотонов, сопровождающиеся увеличением энергии электронов становятся невозможными. Единственно возможными переходами электронов в полупроводнике в рассматриваемых условиях являются переходы зона проводимости - валентная зона, сопровождающиеся рекомбинацией электронно-дырочных пар и испусканием электромагнитного излучения. В полупроводнике создаются условия, при которых происходит усиление электромагнитной волны. Иными словами, коэффициент поглощения получается отрицательным, а рассматриваемая ситуация отвечает состоянию с инверсной плотностью населенности.
Рис. 9.1
Поток квантов излучения, энергия которых находится в пределах от hv=Ec-Ev до hv=Fn-Fp, распространяется через возбужденный полупроводник беспрепятственно.
Для реализации процесса излучательной рекомбинации необходимо выполнить два условия. Во-первых, электрон и дырка должны локализоваться в одной и той же точке координатного пространства. Во-вторых, электрон и дырка должны иметь одинаковые по значению и противоположно направленные скорости. Иными словами, электрон и дырка должны быть локализованы в одной и той же точке k-пространства. Так как импульс образующегося в результате рекомбинации электронно-дырочной пары фотона значительно меньше по сравнению с квазиимпульсими электрона и дырки, то для выполнения закона сохранения квазиимпульса требуется обеспечить равенство квазиимпульсов электрона и дырки, участвующих в акте излучательной рекомбинации.
Оптическим переходам с сохранением квазиимпульса соответствуют вертикальные в k-пространстве (прямые) переходы. Сохранение квазиимпульса в процессе излучательного перехода может рассматриваться как квантомеханическое правило отбора (в том случае, когда в акте излучательной рекомбинации не принимают участие третьи частицы, например, фононы или атомы примесей). Невертикальные в k-пространстве (непрямые) переходы имеют значительно меньшую вероятность по сравнению с прямыми переходами, так как в этом случая требуется сбалансировать некоторый разностный квазиимпульс dk (рис. 9.2).
Таким образом, для получения излучательной рекомбинации необходим прямозонный полупроводник, например, GaAs. Вообще, придерживаясь строгой теории можно доказать, что инверсная населенность возможна лишь при условии Ec-Eg<Fn-Fp.
Широко используемыми на практике способами создания инверсной населенности являются: 1) возбуждение за счет инжекции неосновных носителей через p-n - переход; 2) возбуждение электронным лучом; 3) возбуждение в сильном электрическом поле.
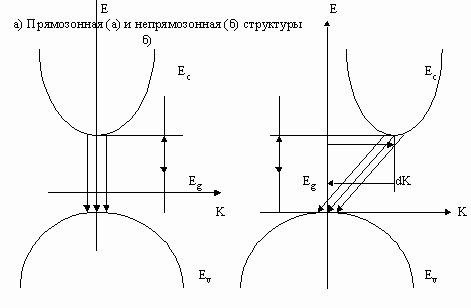
Рис. 9.2
9.2. Лазеры на гетеропереходах
Наиболее легко и эффективно инверсия населенности достигается в p-n-переходах за счет инжекции электронов.
Известно, что в сильнолегированных (вырожденных) полупроводниках, когда одному и тому же значению энергии соответствуют различные электронные или дырочные состояния, в p- и n-областях уровни Ферми находятся в пределах разрешенных зон и при тепловом равновесии эти уровни для электронов и дырок совпадают (рис. 9.3, а).
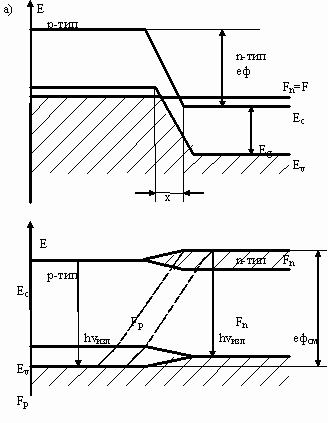
Рис. 9.3,а
В области p—n-перехода образуется потенциальный барьер, не позволяющий переходить основным носителям из зоны в зону. Если же к переходу приложить напряжение U в прямом направлении, то потенциальный барьер в области p—n-перехода уменьшается на значение энергии, соответствующей этому напряжению. Как правило, это напряжение оказывается приложенным к переходу, вследствие чего равновесие носителей тока нарушается. Если при тепловом равновесии распределение электронов и дырок можно было описать с помощью квазиуровня Ферми, то при наличии приложенного электрического поля заполнение состояний нужно рассматривать отдельно для зоны проводимости и отдельно для валентной зоны. При включении прямого смещения возникает диффузионный поток электронов через p—n-переход, который стремится поднять квазиуровень Ферми Fn для электронов в p—n-области до его уровня в n-области. Инжектированные электроны после диффундирования на небольшое расстояние, определяемое диффузионной длинной, рекомбинируют с дырками; в результате возникает стационарное состояние, при котором скорость рекомбинации электронов в точности сбалансирована скоростью их инжекции. Совершенно аналогичны рассуждения и для дырок в валентной зоне. При наличии стационарного состояния положение квазиуровней Ферми для двух типов носителей в области перехода меняется (рис. 9.3, б).
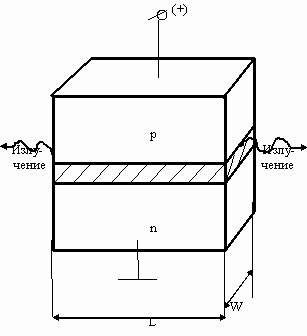
Рис. 9.3,б
Основные носители вытягиваются из контакта, чтобы обеспечить условие нейтральности. В настоящее время лазерные диоды в основном изготовляют из GaAs или Ga1-xAlxAs. Структура лазерного диода на p—n-переходе представлена на Обычно p—n-переход формируется путем эпитоксиального выращивания слоя p-типа на подложке n-типа. Электрический ток является источником энергии накачки, необходимой для создания инверсии населенности в активной зоне, примыкающей к p—n-переходу. Две параллельные торцевые поверхности изготавливаются путем скола по кристаллографической оси для работы в качестве зеркал резонатора и создания положительной оптической обратной связи, необходимой для генерации излучения. В силу большого показателя преломления полупроводникового материала коэффициент отражения от граней составляет 30—35%. Боковые грани лазерного кристалла имеют неровности, для того чтобы подавить поперечное нежелательное распространение света.
К основным параметрам лазерного диода относятся спектр частот излучения (оптические моды), пороговый ток, выходная мощность излучения и эффективность работы. Когда ток проходит через лазерный диод , то свет генерируется за счет инверсии населенности посредством спонтанного и стимулированного излучений. Вследствие отражения от торцов свет многократно проходит через активную область и преимущественно усиливается стимулированным излучением. Внутри лазерного диода устанавливается стоячая волна с целым числом полуволн между торцевыми поверхностями. Модовое число m задается числом полуволн
m = 2Ln/Lw ,
где L — расстояние между торцами; n — показатель преломления; Lw —длинна волны излучения в вакууме. Модовое разделение можно установить, взяв производную dm/dLw . Тогда
dm/dLw=-2Ln/ Lw2+(2L/ Lw)(dn/ dLw).
При dm=-1, что соответствует потере одной полуволны в резонаторе, получим выражение для модового разделения:
dLw= dLw2/{2L[n- Lw(dn/ dLw)]}.
Спектр излучения лазерного диода показан на рис. 8.4. Обычно существует несколько продольных мод, имеющих длины волн вблизи пика спонтанной эмиссии.
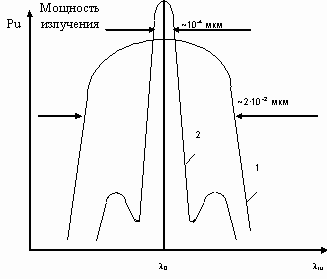
Рис. 9.4
Модовое разделение для полупроводникового лазера на основе GaAs составляет dLw = 0.3 нм. Для того чтобы лазер работал в одномодовом режиме, необходимо каким-либо способом подавить нежелательные боковые моды, оставив основную центральную.
Лазерный диод не сразу начинает излучать при приложении к нему напряжения от внешнего источника. При малом токе имеет место спонтанное излучение (рис. 9.4) с шириной спектра излучения в несколько сот микрометра. По мере нарастания тока накачки в области p—n-перехода создается высокая степень инверсии населенности и излучается больше света. Отдельные фотоны многократно проходят строго в плоскости p—n-перехода и перпендикулярно к торцам диода усиливаются. С возрастанием тока накачки испускаемое диодом излучение существенно сужается одновременно по ширине спектра и по пространственной расходимости. Когда возникает индуцированное излучение, интенсивность излучения увеличивается за счет образования большого количества электронно-дырочных пар в единицу времени. Спонтанное излучение подавляется вследствие того, что образовавшиеся первоначально фотоны повторяют себя при прохождении через активную область. Излучение лазерного диода, полученное при плотностях тока выше порогового, являются когерентными. При этом форма кривой спектрального распределения резко изменяется от широкой кривой распределения спонтанной эмиссии 1 к кривой с несколькими узкими модами 2 (рис. 9.5).
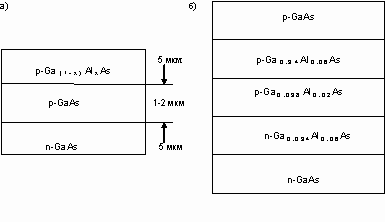 Рис. 9.5
Рис. 9.5
Значение порогового тока в зависимости от природы материала и геометрических параметров можно получить из следующих рассуждений. Пусть в области p—n-перехода существует светоизлучающий слой толщины D, который больше толщины d слоя с инверсной населенностью. Тогда можно предположить, что из всех существующих электронно-дырочных пар только часть d/D остается в активной области и может участвовать в индуцированном излучении.
Положим, что световая волна распространяется в кристалле и на каждую торцевую поверхность падает световой поток мощностью Ps , а коэффициент отражении от торца p. При наличии лазерного излучения произведение pPs экспоненциально увеличивается в зависимости от длины активной зоны L. Существующие потери световой волны значительно перекрываются лазерным усилением за счет индуцированного излучения. Каждый торец диода излучает свет мощностью Pвых/2=(1-p)Ps.. Если µ [см-1[см-1] — коэффициент потерь для волны при ее распространении в кристалле, а H [см-1] — коэффициент усиления, то мощность в зависимости от пройденного волной расстояния вдоль активной области будет
P=pPsexp[H(d/D)-µ]z.
Усиление волны происходит только в области с инверсной населенностью, поэтому величину Н необходимо умножить на d/D, в то время как потери имеют место по всему объему и поэтому коэффициент µ не имеет такого множителя. Тогда при прохождении кристалла длинной L будем иметь:
P=pPsexp[H(d/D)-µ]L;
ln(1/p)=[H(d/d)-µ]L.
Таким образом, условие лазерного излучения имеет вид
H(d/D)=µ+(1/L) ln(1/p). (9.1)
Коэффициент усиления H связан с плотностью инжектированного тока. Выражение для величины Н будет
H=gLw2 I/(8en2dV), (9.2)
где для GaAs при комнатной температуре квантовая эффективность g=0.7, длина волны излучения в вакууме Lw=9.0·10-6 см, показатель преломления n=3.34 при Lw; V — ширина полосы спонтанного излучения, V=1.5·1013 c-1; e — заряд электрона; d —толщина активной области, d=10-4 см; I — плотность инжектируемого тока.
Выражение (9.2) справедливо для допорогового тока. Подставляя (9.2) в (9.1), поучим
(gLw2I)/(8en2VD)=µ+(1/L) ln(1/p). (9.3)
Левая часть в выражении (9.3) описывает усиление волны за один проход, а правая часть — потери. Из (9.3) нейдем значение порогового тока, достаточное для покрытия потерь:
I=(8en2VD)/(gLw2I)(µ+(1/L) ln(1/p)). (9.4)
Слагаемое (1/L) ln(1/p) определяет потери на излучение. Коэффициент отражения может быть выражен через коэффициент пропускания T=1-p, и тогда разложение ln[1/(1-T)] в ряд имеет вид
(1/L) ln(1/p)=(1/L) ln[1/(1-T)]=(1/L) [T-(T2/2)+ (T3/3)- (T4/4)+...].
Пренебрегая членами высокого порядка по Т, найдем
(1/L) ln(1/p)=T/L.
Тогда выражение (9.4) представим в виде
I=(8en2VD)/(gLw2I)(µ+T/L). (9.5)
Формула (9.5) справедлива для приближенных расчетов. Из формулы (9.5) также следует, что для уменьшения I необходимо уменьшать D и наиболее оптимальным условием будет D=d. Но практически это условие трудно осуществить на обычном лазерном диоде, так как генерируемая в окрестности p—n-перехода световая волна распространяется не только в активной области, но и за ее пределами, где не выполняются условия инверсности населенности. Еще одной причиной является то, что часть инжектируемых электронов, обладая большой длиной свободного пробега, протаскивает активную часть p—n-перехода и не участвует в образовании электронно-дырочных пар. По этим причинам необходимо ограничить зону распространения генерируемого света и инжектируемых электронов и обеспечить условия, чтобы эти процессы протекали только в активной области. Желаемые свойства оптического ограничения могут быть получены на гетеропереходных структурах. Самым простым из них является лазер с одинарным гетеропереходом (ОГ), представленный на рис. 9.6,a. Излучающий p—n-переход образуется между GaAS и Ga(1-x)AlxAs посредством специальной технологической обработки. Если концентрации примесей примерно одинаковы на обеих сторонах p—n-перехода, то инжекционный ток будет существовать за счет электронов, инжектируемых в слой p-типа, поскольку эффективная масса электронов почти на порядок меньше эффективной массы дырок. Поэтому слой с инверсной населенностью будет находится в p-GaAs, толщина которого соизмерима с длинной диффузии инжектирумых электронов. Таким образом, область инверсии населенности ограниченна толщиной, где в основном и происходит рекомбинация электронов с последующим излучением.
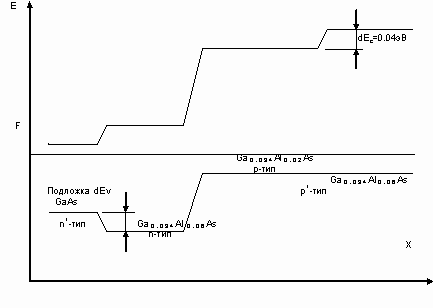 Рис. 9.6, а
Рис. 9.6, а
В ОГ-лезере оптическое ограничение происходит с одной стороны, отсюда желаемый результат т. е. повышение эффективности работы гетеролазера, реализуется частично, а поэтому у ОГ-лазера значение порогового тока выше, чем у лазера с двойной гетероструктурой (рис. 9.6, б). Поскольку удалось уменьшить значение порогового тока у ОГ-лазера, это дало возможность использовать его работу пи комнатной температуре, но только в импульсном режиме накачки. В непрерывном режиме накачки при комнатной температуре работают лазеры с двойной гетероструктурой (ДГ).
Толщина активного слоя ДГ-лазера составляет не менее 1 мкм. При этом по всему слою создается инверсная населенность. Если в ОГ-лазерах толщина активного слоя соизмерима с длинной диффузии инжектируемого электрона, то в ДГ-лазерах толщина меньше этой длины. Кроме того, в ДГ-лазерах обеспечивается оптическое ограничение с двух сторон активной зоны. Эти обстоятельства приводят к тому, что ДГ-лазеры являются высокоэффективными приборами и характеризуются минимальным пороговым током, что позволяет осуществлять непрерывную накачку электрическим током при комнатной температуре.
Для улучшения выходных характеристик гетероструктурного лазера в процессе получения гетероструктуры создают условия, обеспечивающие ограничение носителей заряда в активной области. Для структуры, изображенной на рис. 9.6, б, диаграмма энергитических зон приведена на рис. 9.7. Из-за того, что ширина запрещенной зоны у полупроводника больше в области с увеличением концентрацией атомов Al, возникают смешения в зоне проводимости на p—p+ переходе (dEc) и в валентной зоне на n—p- и n+—p-переходах (dEv).
Когда к такой структуре прикладывается прямое напряжение смещения, электроны инжектируются из n- в p-область. Скачок зоны проводимости на p—p+-границе раздела на dEc обеспечивает энергетический барьер для инжектируемых электронов, производя тем самым ограничение их в p-области и увеличивая вероятность их рекомбинации с дырками. Скачок валентной зоны на n—p-переходе dEc повышает уже существующий потенциальный барьер, препятствующий инжекции дырок в n-область, улучшая тем самым инжекционную эффективность. Таким образом, у двойной гетероструктуры имеет место тенденция ограничения как основных, так и инжектируемых неосновных носителей в активной зоне. Это обеспечивает хорошие условия для получения более эффективной инверсной населенности. Значит ДГ-лазеры обеспечивают более высокие выходные характеристики по сравнению с ОГ-лазерами, и тем более по сравнению с гомопереходными лазерами. Сравнение технических характеристик показывает, что если у гомостктурного лазера пороговая плотность тока равна 104 А/см2 при квантовой эффективности 10%, то у ОГ-лазеров пороговая плотность тока равна 103 А/см2 при квантовой эффективности 40%. Эти лазеры работают только в импульсном режиме. У ДГ-лазеров пороговая плотность тока равна 700— 800 А/см2 , а квантовой эффективность составляет 55%. Эти лазеры работают в непрерывном режиме.
Однако у ДГ-лазеров большая угловая расходимость луча (20— 40°) в плоскости, перпендикулярной к плоскости перехода, из-за дифракции света в тонком активном слое, в то время как у гомоструктурных и ОГ-лазеров угловая расходимость составляет 15— 20°. У всех рассмотренных типов лазеров угловая расходимость луча в плоскости перехода составляет не более 10°.
9.3. Открытый оптический резонатор
Открытым оптическим резонатором называют систему, состоящую из двух обращённых друг к другу отражающих поверхностей, в которой могут возбуждаться электромагнитные колебания оптического диапазона. Отражающими поверхностями могут быть зеркала различной формы (плоские, сферические, параболические), грани призм полного внутреннего отражения, границы раздела сред с различными показателями преломления. Простейшим открытым оптическим резонатором является система из двух параллельных зеркал, находящихся на определённом расстоянии друг от друга. Эффективное взаимодействие электромагнитного поля с активной средой осуществляется при помещении её в резонатор, который должен быть таким, чтобы можно было разместить внутри него достаточное количество активного вещества. Активное вещество может заполнять рабочий объём резонатора частично или полностью.
Задача резонатора лазера – обеспечить, чтобы возникающее внутри него вынужденное излучение многократно проходило через активную среду, способную усиливать проходящее через неё излучение. Таким образом, с помощью резонатора получается положительная обратная связь. Для вывода полезного излучения из резонатора его зеркала делаются частично прозрачными (полупрозрачными).
Резонатор во многом определяет основные свойства выходного излучения: степени монохроматичности и когерентности, направленность и мощность. Нормальные типы колебаний (моды) резонатора можно рассматривать как результат интерференции плоских волн, распространяющихся от одного зеркала к другому. В результате в резонаторе образуются стоячие волны.
Нормальные типы колебаний открытого резонатора обозначают Тmnq, чтобы показать, что векторы электрического и магнитного полей в большинстве случаев перпендикулярны продольной оси резонатора. Индексы m,n,q – целые числа; q равно числу полуволн, укладывающихся вдоль оси резонатора между его зеркалами.
Типы колебаний с различными m и n называют поперечными. Они отличаются друг от друга распределением амплитуды и фазы поля на поверхностях зеркал, а также дифракционными потерями. Типы колебаний, имеющие одни и те же значения m и n, но разное q, называют продольными. Они отличаются друг от друга резонансной частотой. Интервал между частотами двух соседних, различающихся по величине q на единицу, продольных колебаний в резонаторе с плоскими параллельными бесконечно протяженными зеркалами, составляет
![]()
где c – скорость света; L – расстояние между зеркалами.
В лазерах сначала применялись резонаторы с плоскими зеркалами. В настоящее время такие резонаторы используются в твердотельных и полупроводниковых лазерах. Одним из достоинств резонаторов с плоскими зеркалами является максимальная направленность выходного излучения.
Резонаторы, образованные двумя сферическими зеркалами с равной кривизной, находящимися друг от друга на расстоянии радиуса кривизны, называются конфокальными резонаторами.
Часто используются полусферические резонаторы, у которых одно зеркало плоское, а второе – сферическое. Длина такого резонатора равна половине радиуса кривизны сферического зеркала. Резонатор имеет низкие потери и мало критичен к изменению расстояния между зеркалами. Открытые резонаторы по сравнению с закрытыми тех же размеров имеют значительно более разряжённый спектр собственных частот.
Условия самовозбуждения, как обычно, включают в себя баланс фаз и баланс мощностей.
Рассмотрим резонатор на рис.9.7, полностью активной средой. Обозначим через Г1 и Г2 комплексные коэффициенты отражения от зеркал, L – расстояние между зеркалами. Предположим, что в некоторый момент времени вблизи зеркала 1 возникло спонтанное излучение, которое распространяется к зеркалу 2. Поле А 1 при движении внутри резонатора взаимодействует с веществом и у зеркала 2 будет иметь вид где ixp = ik - постоянная распространения; xа – показатель усиления активной среды; k – фазовая постоянная; аа – показатель потерь активной среды, учитывающий потери вследствие рассеяния излучения на неоднородностях после отражения от зеркала 2.
![]() .
.
Здесь коэффициент x учитывает дифракционные потери при отражении от зеркала. После А¢ 2 при обратном распространении к зеркалу 1 вновь усиливается в активной среде и после отражения от зеркала 1 можно записать
![]() (9.6)
(9.6)
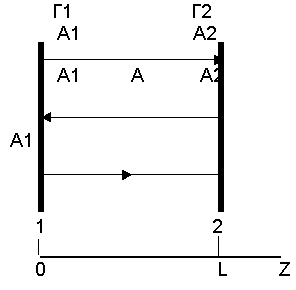
Рис. 9.7
Из (1) получаем условие стационарности колебаний
![]() (9.7)
(9.7)
комплексные коэффициенты отражения представим в виде, где Г1, Г2 – модули коэффициентов отражения; D j и D j 2 - изменение фазы волны при отражении от зеркал. Подставляя Г1, Г2 и Xp в (9.7) и учитывая, что k = 2 P / l , после разделения действительной и мнимой частей (9.7) получаем соответственно условия баланса фаз и амплитуд:
![]()
![]() (9.8)
(9.8)
![]() (9.9)
(9.9)
Условие (9.8) означает, что волны, пройдя путь 2L в резонаторе и дважды отразившись от зеркал, получают фазовый сдвиг, кратный целому числу периодов. В генераторе создаётся положительная обратная связь. Условие баланса фаз определяет частоту лазерного излучения. Так как (9.8) выполняется на любой резонансной частоте оптического резонатора, то на каждой из этих частот может быть генерация, если будет выполнено условие баланса амплитуд.
Согласно (9.9) колебания в лазере будут существовать лишь в том случае, если усиление в активной среде компенсирует все потери в резонаторе. Логарифмируя (9.9) , получаем
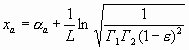 (9.10)
(9.10)
Второе слагаемое в (9.10) учитывает потери в зеркалах, в том числе на полезное излучение. Мощность генерации Рген в стационарном режиме, определяемая из баланса мощностей, равна сумме мощностей потерь в среде и зеркалах и пропорциональна (аа + а3). Если пренебречь рассеянием и поглощением в зеркалах, то мощность потерь будет равна мощности излучения, выходящего из резонатора через зеркало. Последнюю назовём мощностью излучения Ризл.
Pизл/ Pген= a 3 / ( a а+ a 3 ) .
Выходящая из резонатора мощность Ризл зависит от коэффициентов пропускания зеркал и при увеличении а3 растёт, достигая максимума, а затем уменьшается до нуля, когда потери станут настолько большими, что условие самовозбуждения не выполняется. Таким образом, можно подобрать оптимальный режим работы лазера.
9.4. Характеристики излучения в оптическом диапазоне
Одной из характеристик оптического излучения является ширина спектра, т.е. область частот, в которой происходит излучение. Ширину спектра можно оценить с помощью понятия степени монохроматичности излучения
m =D v/ v0 (9.11)
где v0 - центральная частота; D v - ширина спектра, взятая на уровне половинной мощности. Гармоническое колебание называется монохроматическим, если оно определяется выражением
a(t)= A sin(2P v0t+j ),
где амплитуда А, круговая частота 2P v0 и начальная фаза j 0 не зависят от времени.
Монохроматическое излучение характеризуется значением m =0, если даже m < < 1 , то излучение почти монохроматическое или, иначе, квазимонохроматическое.
Уточним теперь понятие когерентности излучения. Различают пространственную и временную когерентность. Если существует согласованность между фазами колебаний, излучаемых одним и тем же источников различные моменты времени в одной и той же точке, то говорят о временной когерентности этих колебаний. Пространственная когерентность - это наличие связи между фазами колебаний в разных точках пространства в один и тот же момент времени.
При сложении когерентных колебаний возникает устойчивая интерференция, если колебания некогерентны, то разность фаз двух колебаний непрерывно меняется, причём за достаточно большое время принимает равновероятно всевозможные значения от 0 до 2П и интерференция не наблюдается. В общем случае связь (корреляция) колебаний в точке пространства будет наблюдаться только в некотором интервале времени, называемом временем когерентности. Расстояние, проходимое светом за время когерентности, называют длиной когерентности.
Длина когерентности в лазерах из-за большого времени когерентности на много порядков больше, чем в обычных источниках света. Пространственная когерентность характеризует форму волнового фронта излучения. В лазерах излучение имеет высокую направленность, определяемую свойствами оптического резонатора.
Высокая степень временной когерентности излучения определяет применение лазеров в системах передачи информации, измерения расстояний и угловых скоростей и в квантовых стандартах частоты. Высокая степень пространственной когерентности (направленности) позволяет эффективно передавать световую энергию и фокусировать световой пучок в пятно очень малого размера.
9.5. Газовые лазеры
Газовыми лазерами называются оптические квантовые генераторы, в которых активной средой является газ, смесь нескольких газов или смесь газа с парами металла. В зависимости от того, состояния каких частиц используются для получения инверсии населённостей, различают атомные, ионные и молекулярные лазеры.
Газовые лазеры являются наиболее распространенным в настоящее время типом лазеров. Они излучают на волнах от ультрафиолетового до инфракрасного диапазона (0,15 – 699, 5 мкм) и обладают самой высокой степенью когерентности выходного излучения по сравнению со всеми остальными источниками света. Газовая среда обладает хорошей оптической однородностью, поэтому можно получить наименьший угол расхождения пучка.
9.6. Гелий-неоновый атомный лазер
Активной средой является смесь двух газов – гелия Не и неона Ne, а лазерными уровнями – энергетические уровни возбуждённых атомов неона. Для создания инверсии населенностей используют электрическую накачку путём создания тлеющего разряда в газоразрядной трубке. При разряде вследствие неупругих соударений со свободными электронами происходит возбуждение атомов гелия. Энергия возбуждённых атомов Не передаётся далее атомам неона. Атомы гелия являются посредниками при передаче энергии от быстрых электронов к атомам неона. Поэтому гелий можно назвать вспомогательным, а неон – основным, или рабочим, газом. С ростом общего давления в смеси увеличивается концентрация атомов гелия и неона и растут населенность возбуждённых уровней и выходная мощность. Однако при высоком давлении, когда концентрация частиц в разряде становится большой, уменьшается длина свободного пробега электрона и соответственно уменьшается энергия, приобретаемая электроном на этом пути в электрическое поле. Последнее приводит к уменьшению энергии, передаваемой атомам гелия, и к снижению мощности излучения. Оптимальное давление примерно 100 Па.
9.7. Ионные лазеры
В этих лазерах используются энергетические переходы между уровнями возбуждённых ионов. Применяются чистые инертные ионы: аргон, криптон, ксенон, неон, а также ионизированные пары различных химических элементов (селена, цинка, йода). Энергетические уровни основного и возбуждённого состояний иона расположены гораздо выше уровней возбуждённых состояний нейтральных атомов, поэтому вероятность прямого возбуждения этих уровней очень мала. Наиболее распространенным из ионных лазеров является аргоновый лазер, работающий на квантовых переходах между возбуждёнными состояниями иона Ar + в видимой части спектра.
Мощность излучения ионных лазеров выше, чем лазеров, работающих на атомных переходах.
9.8. Молекулярные лазеры
Недостатком атомных и ионных лазеров является их низкий КПД, который объясняется тем, что верхний рабочий уровень расположен очень высоко над основным состоянием и поэтому в процессе возбуждения принимает участие лишь малая доля общего числа электронов. Для повышения КПД можно использовать колебательные возбужденные состояния молекул, энергетические уровни которых расположены значительно ближе друг к другу, чем электронные. Это облегчает генерацию колебаний и позволяет получить излучение в инфракрасном диапазоне. Для возбуждения молекулярных лазеров используются различные способы накачки: электрический разряд, химическая, оптическая и тепловая накачки. Наиболее распространенным молекулярным лазером является лазер на углекислом газе СО2, который имеет очень хорошие параметры: высокие выходную мощность и КПД как в непрерывном, так и в импульсном режимах. Используется смесь рабочего углекислого газа с азотом N2, в которую добавлен гелий. Гелий добавляют для увеличения теплопроводности смеси и улучшения отвода тепла от центра к стенкам газоразрядной трубки, что способствует уменьшению населенности нижних рабочих уровней и повышению мощности лазера.
Особенностью лазера на СО2 является необходимость постоянного движения газа через газоразрядную трубку, так как число молекул постоянно уменьшается в результате диссоциации на кислород и окись углерода: 2СО2 2СО+О2. Если не восполнить убыль СО2, мощность лазера через некоторое время заметно уменьшится. Конструкции лазеров на СО2 и гелий-неоновой смеси имеют много общего. Дополнительные требования связаны с большей выходной мощностью лазеров на СО2 – это необходимость охлаждения и повышенная термостойкость окон и зеркал. Наибольшая мощность излучения получена в лазере с прокачкой газовой смеси вдоль оптической оси резонатора. Достигнута максимальная мощность 8,8 кВт в непрерывном режиме работы, при этом КПД составил 15 –20% . импульсный режим работы лазера облегчает решение проблемы теплоотвода. В импульсном лазере при длине трубки 3м и длительности импульса 90нс достигнута максимальная импульсная мощность излучения около 100 Мвт.
9.9. Газодинамический лазер
Советскими учёными В.К. Конюховым и А.М. Прохоровым в 1966 году был предложен инфракрасный газодинамический лазер на углекислом газе в смеси с азотом, с охлаждением в сверхзвуковом сопле. Такой лазер был создан в 1970 году. Инверсия населённостей уровней возникает в газодинамическом лазере при быстром (сверхзвуковом) расширении предварительно нагретой газовой смеси. При сжигании топлива в камере сгорания получается углекислый газ, который здесь же смешивается в определённой пропорции с азотом и водяным паром, образуя высокотемпературную плазму. Газовая смесь под давлением 1700Па со сверхзвуковой скоростью проходит через сопло 1(2, 3-полупрозрачное и отражающее зеркала резонатора) и за ним расширяется и охлаждается.
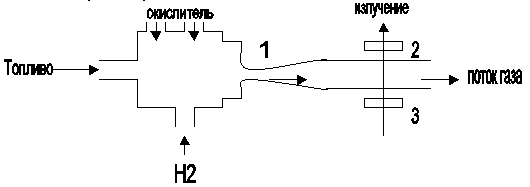
Рис. 9.8
Вследствие относительно большого времени жизни верхнего уровня молекулы СО2 и малого времени прохождения газа через сопло населённость возбужденного при нагреве газа верхнего уровня сохраняется за время движения молекул от камеры сгорания до оптического резонатора. Значительно меньше время жизни частицы на нижнем уровне приводит к тому, что населённость нижнего уровня оказывается много меньше населённости верхнего уровня уже на расстоянии нескольких сантиметров от сопла. Таким образом, создаётся инверсия населённостей уровней, и газ поступает в резонатор, состоящий из двух зеркал, параллельных потоку. Мощность излучения газодинамического лазера определяется расходом вещества и энергией, запасённой при нагревании газа. В газодинамическом лазере тепловая энергия газа в форме колебательного движения молекул непосредственно превращается в направленное когерентное электромагнитное излучение. В непрерывном режиме получена мощность излучения несколько сотен киловатт (500 кВт) при пока малом КПД (0, 5 – 1%).
9.10. Лазеры на твёрдом теле
Твердотельными называют лазеры, в которых активной средой являются кристаллические и аморфные диэлектрики (стёкла), легированные ионами хрома или редкоземельных элементов. Концентрация активных частиц в твёрдом материале намного превышает концентрацию частиц в газовых средах. Поэтому можно получить большую населённость уровней, а, следовательно, и большую мощность излучения на единицу объёма, чем в газовых лазерах, или ту же мощность при малой длине активной среды. Однако длина активных элементов твердотельных лазеров ограничивается имеющимися оптическими неоднородностями вещества, приводящими к рассеиванию излучения и понижению добротности резонаторов. Обычно длина активных элементов несколько десятков элементов.
В первом твердотельном лазере (1960 год) использовался рубин. Рубин – это корунд Al2O3, в кристаллической решётке которого часть ионов алюминия замещена ионами Cr с зарядом 3+. в зависимости от процентного содержания примеси корунд окрашивается от розового до тёмно-красного. В твёрдых телах сильное взаимодействие частиц приводит к существенному увеличению ширины энергетических уровней. Инверсия населённостей создаётся по трёхуровневой схеме.
Рис. 9.9
Производится оптическая накачка путём облучения мощной ксеноновой лампой. Ионы хрома поглощают излучение и переходят из основного состояния 1 на два широких уровня 3. Подуровни 2 являются метастабильными (время жизни около 3·10 с). Время жизни уровней 3 определяется безызлучательными релаксационными переходами на подуровни 2. Это много больше времени жизни, связанного со спонтанными излучательными переходами. Вследствие безызлучательных переходов происходит быстрое уменьшение населенности подуровней 3 и заселение метастабильных подуровней 2. Поэтому населенность подуровней 2 может стать больше населенности основного уровня 1. Так как разрешены переходы в основное состояние с верхнего и с нижнего подуровней 2 , то возможна генерация в красной области спектра с длинами волн l = 0 , 6 9 3 и 0 , 6 9 2 9 мкм.
Рубиновые лазеры могут работать как в импульсном, так и в непрерывном режимах. Система оптической накачки содержит лампу и элементы, обеспечивающие концентрацию светового потока на активный стержень.
Импульсный режим работы ламп обеспечивается разрядом конденсаторов, предварительно заряжаемых от источника напряжением до нескольких киловольт. Для работы в непрерывном режиме используются специальные дуговые капиллярные лампы и лампы накаливания.
При использовании в качестве активных частиц ионов редкоземельных элементов (неодима, диспрзия, самария, эрбия, гольмия и празеодима) инверсия населенностей создаётся по четырёхуровневой схеме. Здесь нижний уровень лазерного перехода находится на достаточно большом расстоянии от основного уровня. В этом случае населенность нижнего уровня оказывается небольшой даже при комнатной температуре. Наиболее распространенным лазером такого типа является лазер на стекле, активированном неодимом. Длина излучения такого лазера l = 1 , 0 6 мкм.
Рассмотрим ещё один лазер, перспективный для использования в оптических системах связи. Это лазер на иттрий-алюминиевом гранате (YAG) Y3Al5O12. Инверсия населённостей создаётся по четырёхуровневой системе. Иттрий-алюминиевый гранат с примесью неодима является уникальным материалом, обладающим хорошей теплопроводностью, большой твёрдостью и удовлетворительными оптическими свойствами.
Стержень Nd: YAG 1 c длинной 5 мм и толщиной 0, 5 мм накачивается с торца GaAlAs- светодиодом 2(3- пластина для теплоотвода).
Для лазера используются кристаллы неодим-пентафосфат NdP5O14. Накачка осуществляется светодиодом при l = 1 , 0 5 мкм. Лазер имеет низкий порог накачки – примерно 1 мВт. Малые размеры лазера позволяют его называть микролазером.
Рис. 9.10
9.11. Жидкостные и химические лазеры
Жидкостные лазеры. Жидкостным называют лазер с жидкостной активной средой. В этих лазерах можно обеспечить примерно такую же концентрацию активных частиц, как в твёрдотельных, и, следовательно, получить высокий энергосъём с единицы объёма активной средой. Важным преимуществом жидкой активной среды является отсутствие потерь излучения из-за неоднородности структуры активного вещества. Нет технологических трудностей, связанных с изготовлением стержней, необходимых для твердотельных лазеров. Легко решается проблема отвода тепла: для этого достаточно применить циркуляцию жидкости в резонаторе.
В лазерах на неорганических соединениях используются растворы солей неодима Nd в окислохлориде селена SeOCl2, свойства иона неодима в растворе подобны свойствам этого иона в кристаллической решётке. Используются те же уровни, что и в твердотельных лазерах на стёклах с примесью неодима. Недостатком раствора на основе SeOCl2 является его токсичность и высокая коррозионная активность.
Конструкция жидкостного лазера подобна конструкции твердотельного с тем отличием, что вместо стержня в резонатор помещается кювета с раствором. Инверсия, как и в твердотельном лазере, осуществляется с помощью оптической накачки от импульсных ламп. Лазеры на основе неорганических сред работают только в импульсном режиме. Средняя мощность излучения достигает 380Вт, а импульсная 50 МВт (в режиме модуляции добротности). В лазерах на основе органических красителей используются растворы родамина, пиронина, трипафламина. Растворителями служат вода, спирты, глицерин и т.д. Лазеры на красителях обладают большим коэффициентом усиления и невысоким порогом накачки. Это позволяет создавать малогабаритные лазеры с перестраиваемой длиной волны.
Химические лазеры. Химическими называют лазеры, в которых инверсия создаётся во время химической реакции, приводящей к образованию атомов или молекул в возбуждённом состоянии. Химические лазеры можно разделить на три группы в зависимости от способа осуществления химической реакции. Это либо фотодиссоциация молекул, либо диссоциация молекул при электрическом разряде в газе, либо взаимодействие соответствующих молекул и атомов и их соединений.
В первой группе при достаточно высокой энергии фотонов внешнего излучения молекула распадается на атомы, при этом один из атомов распавшейся молекулы может оказаться в возбуждённом состоянии, пригодном для получения инверсии населенностей.
Рассмотрим теперь лазеры второй группы. Здесь диссоциация молекул происходит при электрическом разряде в газе. Например в смеси неона и кислорода Ne-O2 путём передачи энергии от метастабильных атомов неона к молекуламО2 происходит возбуждение молекул кислорода, которые, будучи энергетически неустойчивыми, диссоциируют на атомы кислорода, один из которых будет находиться в возбужденном состоянии. Происходит излучение с длиной волны l = 0 , 8 4 4 6 мкм.
Интересны химические лазеры, работающие на прямом преобразовании энергии химических реакций в энергию когерентного оптического излучения. Желательно, чтобы при этом не требовались дополнительные внешние источники света. Лазер состоит из камеры предварительного смешивания реагентов, зоны химической реакции, которая может одновременно являться и активной зоной генерации вынужденного излучения.
9.12. Полупроводниковые лазеры
Рис. 9.11
Общие сведения. В полупроводниковых лазерах используется инверсия населённостей, получаемая в полупроводниках с одним или с различными типами проводимости (p-n-переход).
Идеальным было бы состояние (рис. 9.11), когда верхние уровни в области 2 полностью была бы заполнены электронами проводимости, а нижние в области 1 полностью свободны от валентных электронов, т.е. полностью заполнены дырками. В этом случае инверсия населённости была бы наибольшей.
Формально полупроводник, в котором большинство уровней в области 2 зоны проводимости занято электронами, а в области 1 валентной зоны – дырками, можно назвать вырожденным одновременно для электронов и дырок, в то время как обычно удаётся создать либо электронные, либо дырочные вырожденные полупроводники. Предположим, что в такой полупроводник попадает фотон с энергией hv, большей ширины запрещённой зоны D x , соответствующей границам областей 2 и 1, заполненных электронами и дырками:
D x 0< hv < D x . (9.12)
При этом условии будут происходить вынужденные переходы из области 2 в область 1 с испусканием новых фотонов. Если энергия падающего фотона hv> D x , то начнётся поглощение квантов и возникнут переходы из области 3 валентной зоны, где есть валентные электроны, на свободные уровни области 4 зоны проводимости.
В вырожденном электронном полупроводнике верхняя граница заполненной электронами области 2 в зоне проводимости приблизительно совпадает с уровнем Ферми для электронов x Fт, а в вырожденном дырочном нижняя граница заполненной дырками области 1 в валентной зоне – с уровнем Ферми для дырок x Fp.
Поэтому
D x = x F n- x Fp (9.13)
и условие (11.12) дла получения вынужденного излучения запишем
D x 0< hv< ( x Fn- x Fp) .
Вынужденное излучение будет появляться при воздействии фотонов с энергией, заключенной в пределах hvmin=D x 0 до hvmax=D x =x Fn-x Fp. Такие фотоны всегда есть в полупроводнике вследствие процесса рекомбинации электронов и дырок. Рекомбинационное излучение имеет спонтанный характер, т. е. фотоны распределены хаотически по времени, направлению и поляризации. “Спонтанные” фотоны вызывают вынужденное излучение, однако для получения самовозбуждения необходимо обеспечить многократное прохождение излучения через среду с инверсией населенности. Достигается это созданием отражающих поверхностей на торцах полупроводника.
В полупроводниковых лазерах можно получить очень большие инверсию населенностей и усиление на единицу длины вследствие высокой концентрации частиц в твердом теле. Поэтому длину образца полупроводника можно уменьшить до долей миллиметра, а требования к коэффициенту отражения зеркал снизить.
В полупроводниках возможны следующие методы получения инверсии населенностей: инжекция носителей через p-n переход (инжекционные лазеры), электронная накачка и оптическая накачка. Наибольшее распространение получил метод инжекции носителей.
9.13. Инжекционный лазер
Рис. 9.12
В инжекционных лазерах используется p-n переход, образованный вырожденными полупроводниками с разным типом проводимости. На рис. 9.12, а показана энергетическая диаграмма такого p-n перехода в состоянии равновесия, т. е. при отсутствии внешнего напряжения, а следовательно, и тока через переход. Уровни Ферми x Fn и x Fp в обеих областях совпадают. Приближенно можно считать, что в n-области электроны проводимости располагаются на уровнях между “дном” зоны проводимости x пр и уровнем Ферми x Fn, а в p-области дырки – между “потолком” валентной зоны x в и уровнем Ферми x Fn. Энергетическая диаграммы для случая, когда к p-n переходу приложено прямое напряжение U0, показано на рисунке 9.12 б. Понижение потенциального барьера на величину U0 увеличивает поток электронов из n-области и поток дырок из p-области через переход. Через p-n переход течет ток, и вблизи перехода установится некоторое распределение концентрации неравновесных носителей заряда.
Известно, что при неравновесном состоянии теряет смысл понятие уровня Ферми. Однако для определения полной концентрации носителей в неравновесном состоянии можно воспользоваться прежними формулами, если вместо уровней Ферми ввести квазиуровни Ферми для электронов и дырок. Вдали от перехода (рис. 9.12, б), где сохраняется равновесное состояние, применимы обычные уровни Ферми x Fn и x Fp. В области перехода, где имеются неравновесные носители, существуют два квазиуровня Ферми – для электронов x ’Fn и для дырок x ’Fp. Обычно предполагают, что в пределах перехода до пересечения линии x Fn с границей зоны проводимости величины x Fn и x ’Fn мало отличаются.
Аналогичное предположение дают и для уровней x Fp и x ’Fp. Далее кривая квазиуровня электронов x ’Fn опускается и сливается с уровнем Ферми x Fp. Соответственно, кривая квазиуровня для дырок x ’Fp поднимается и сливается с уровнем Ферми x Fn.
В некоторой области перехода с шириной d одновременно велико число электронов проводимости в группе уровней D x пр и дырок в группе уровней D x в. Поэтому в области d распределение носителей зарядов подобно распределению их на рисунке 9.12, и в ней можно получить инверсию населенностей. В этой области перехода наблюдается наиболее интенсивная рекомбинация электронов и дырок, так как скорость рекомбинации пропорциональна произведению концентраций электронов и дырок, а они в рассматриваемой области велики. Рекомбинация электронов и дырок в переходе сопровождается спонтанным излучением с энергии, большей ширины запрещенной зоны hn > D x 0.
С увеличением внешнего напряжения U0 растут концентрации электронов и дырок в области d перехода, увеличивается инверсия населенности. При некотором пороговом напряжении, когда вынужденное излучение, вызванное спонтанным излучением, достаточно для компенсации потерь света в материале полупроводника и в отражающих поверхностях, наступит генерация. Таким образом, p-n переход при малых токах является источником спонтанного (рекомбинационного) излучения (светодиод), а при токах более порогового – источником когерентного излучения (лазер).
Пороговый ток сильно зависит от температуры и концентрации примесей. Понижение температуры облегчает вырождение полупроводника и, следовательно, уменьшает пороговый ток. Лазеры на арсениде галлия работают при температуре жидкого гелия 4,2 К или жидкого азота 77 К. В настоящее время появились инжекционные лазеры, работающие при комнатной температуре. Экспериментально установлено, что измерение температуры от 4,2 К до комнатной может привести к увеличению плотности порогового тока до 100 раз. При комнатной температуре необходима плотность порогового тока 105 А/см2.
Распространение получил инжекционный лазер на основе вырожденного арсенида галлия GaAs, конструкция которого показана на рисунке 9.13. Две грани полупроводника перпендикулярны плоскости p-n перехода, чтобы не создавать в этом направлении условий для самовозбуждения. Размеры сторон полупроводника – порядка нескольких десятых долей миллиметра. Излучение выходит из узкой области p-n перехода перпендикулярно параллельным граням полупроводника.
Рис. 9.13
Изучение инжекционного лазера имеет большую угловую расходимость вследствие дифракционных явлений в резонаторе. Пусть толщина области p-n перехода, в которой происходит генерация, d = 1 мкм, а расстояние между зеркалами L = 0,1 мм. Тогда число Френеля при l = 1 мкм N = 10-2. При таком малом числе Френеля потери велики, а угловая расходимость составляет 5-6 градусов. Однако в другой плоскости (плоскости p-n перехода) угловая расходимость меньше (примерно 1 градус), т. к область излучения здесь примерно на порядок больше.
Спектр излучения инжекционного лазера зависит от выходной мощности, которая, в свою очередь, определяется плотностью тока через р-n переход. Когда плотность тока незначительно превышает пороговую плотность тока, имеется только одна мода с шириной линии излучения около 0.5 А, и длинной волны λ=0.84 мкм (8400А),
Соответствующий ИК-диапазону. С ростом плотности тока число мод увеличивается. Частота генерируемых мод зависит от температуры, так как последняя влияет на коэффициент преломления кристалла и ширину запрещенной зоны. При измерении температуры возможен перескок от одной моды к другой. Поэтому долговременная стабильность частоты оказывается гораздо меньше, чем у газовых лазеров. Следует отметить, что излучение инжекционных лазеров поляризовано.
Обычно инжекционные лазеры работают в импульсном режиме, при этом максимальная мощность в импульсе ограничивается перегревом кристалла и зависит от рабочей температуры, и длительности импульса. Наибольшая импульсная мощность при температуре жидкого азота в лазерах на GaAs составила 100 Вт, при длительности импульсов примерно несколько микросекунд и частоте следования до 10 кГц. Основным достоинством инжекционных лазеров является возможность модуляции излучения изменением напряжения на p-n переходе.
Коэффициент полезного действия инжекционных лазеров ограничивается в основном следующими причинами. Во-первых ,часть электронов, двигающихся в p-n переходе вследствие большой длинны свободного пробега проходит активную область, не участвуя в создании вынужденного излучения. Во-вторых, генерируемое световое излучение распространяется не только в активной области, но и рядом с ней, где отсутствует инверсия населённости, и, следовательно, происходит поглощение излучения. Кроме этих причин имеется потеря мощности источника питания, связанная с прохождением тока, через области и контакты. Поэтому КПД инжекционных лазеров, на основе GaAs обычно составляет несколько процентов, хотя при оптимальных условиях может достигать десятки процентов.
Советскими учёными Ж. И. Алфёровым и другими предложены инжекционные лазеры на основе гетеропереходов (гетеролазеры), имеющие высокий КПД. В этих лазерах используют полупроводниковые материалы, с различной шириной запрещённой зоны.
Полупроводниковая структура гетеролазеров (рис. 9.14, а) состоит из области GaAs n-типа, узкой областью GaAs p-типа, области тройного соединения AlxGa1-xAs p-типа. Активной является средняя область, где создается инверсия населённости. На границе средней и правой области создаётся потенциальный барьер, который ограничивает длину свободного пробега электронов, инжектируемых из левой области, и повышает эффективность образования вынужденного излучения.
Рис. 9.14
Кроме этого, одновременно уменьшается поглощение света в правой неактивной области, так как из-за различия в коэффициентах преломления в средней и правой областях (рис.9.14, б) наблюдается полное внутреннее отражение света на их границе (волноводный эффект). В СССР разработаны гетеролазеры, с полным внутренним отражением света с обеих сторон от активного слоя, лазеры с двойной гетероструктурой, или ДГС-лазеры. В этих лазерах удалось существенно понизить плотность порогового тока, и получить большой КПД, что позволило при комнатной температуре осуществить режим непрерывного излучения, который был ранее возможен,только при температуре жидкого азота. В ДГС-лазерах, на основе GаAlAs при комнатной температуре получена плотность порогового тока не менее 1кА/см2.
Отличительными особенностями гетеролазеров является высокий КПД, удобство возбуждения, малые габариты. Путём изменения концентрации примесного алюминия от 0 до 30 % в AlxGa1-xAs можно изготовлять лазеры с различной длинной волны излучения в пределах 0,9-0,68 мкм. Преимущества полупроводниковых лазеров заключается в простоте модуляции излучения, осуществляемого изменением тока накачки.
Недостаток полупроводниковых лазеров – невысокая степень когерентности излучения, плохая температурная и радиационная устойчивость и пока ещё низкая долговечность: так, в лабораторных условиях получена долговечность 104 ч., однако в промышленных образцах она на порядок ниже.
Крупным достижением лазерной техники последних лет явилось создания гетеролазера с распределённой обратной связью. В таком полупроводниковом лазере торцевые зеркальные поверхности, образующие оптический резонатор, заменены дифракционной решеткой, которая, как известно на определённых частотах полностью отражает падающее на неё излучение.
Повышение мощности излучения инжекционных лазеров добиваются изготовлением набора (решёток) лазерных диодов. Например, при комнатной температуре получена импульсная мощность от 10 до 1000 Вт при частоте следования импульсов до 1кГц и длительностью импульсов 70-200 нс. При этом число лазерных диодов в решётке колеблется от 10 до 60.
При температуре жидкого азота в решётке из 1000 лазерных диодов получена средняя мощность 30-40 Вт. Вследствие низкой температуры КПД оказывается высоким (около нескольких десятков процентов). Импульсная мощность решётки составляла 1.5-2.5 кВт для длительности импульсов 2мкс, при частоте следования 10 кГц.
9.14. Применение лазеров в технике связи
Изобретение лазеров создало предпосылки для создания оптических линий связи очень большой информационной емкости, так как частота его колебаний лежит примерно в области 5× 108 МГц, что в 100 тыс. раз выше, чем частота существующих в настоящее время высокочастотных систем связи. Однако в скоре после первых экспериментов стало ясно, что открытая атмосфера является далеко не оптимальной средой для передачи излучения. Линия связи должна быть защищена от воздействия различного рода осадков и температурных изменений, так как наличие дождя, тумана, снега, пыли значительно увеличивает затухание и связь прекращается.
Наиболее перспективной направляющей системой для оптической связи оказались диэлектрические волноводы или волокна, как их называют из-за малых размеров и метода получения. В 1972 г. Затухание в волоконных световодах было 20 дБ/км, а в 1979 г. Его удалось снизить до 0,2 дБ/км. Успехи в технологии получения световодов с малыми потерями стимулировали работу по созданию волоконно-оптических линий связи ВОЛС, которые обладают рядом преимуществ по сравнению с обычными кабельными линиями:
- высокая помехоустойчивость, нечувствительность к внешним электромагнитным полям и практически отсутствие перекрестных помех между отдельными волокнами, уложенными вместе в кабель;
- значительно большая широкополосность;
- малая масса и габариты; ожидается уменьшение массы и габаритов примерно в 10 раз по сравнению с существующими кабельными системами связи при одинаковом числе каналов связи. Это приведет к уменьшению стоимости и времени прокладки оптического кабеля;
- полная электрическая изоляция между входом и выходом системы связи, поэтому не требуется общее заземление передатчика и приемника. Можно производить ремонт оптического кабеля, не выключая оборудования;
- отсутствие коротких замыканий; волокна могут быть использованы для пересечения зон с горючими и легковоспламеняющимися средами без боязни коротких замыканий, являющихся причиной пожара;
- потенциально низкая стоимость; хотя волокна изготавливаются из сверхчистого стекла, имеющего примеси меньше чем несколько частей на миллион, при массовом производстве их стоимость должна быть невелика. Кроме того, в производстве волокон не используются такие дорогостоящие цветные металлы, как медь и свинец, запасы которых на земле ограничены.
Оптические волокна должны иметь малое затухание в тех участках спектра, где существуют источники излучения. Для ВОЛС в качестве источников изучения используются лазеры и светодиоды. Передатчики ВОЛС должны работать при комнатной температуре, не требовать специальной системы охлаждения, быть компактными и удобными в обслуживании, иметь большую надежность. Наиболее перспективным лазером является полупроводниковый лазер с двойной гетероструктурой. В таких лазерах путем изменения тока можно осуществлять модуляцию излучения до 1 ГГц.
Для ВОЛС на короткие расстояния в качестве источника излучения используются световоды. Излучение световода из арсенида галлия соответствует инфракрасной области спектра (l » 0,9 мкм), где волокна обладают малыми потерями. Эти световоды имеют большой КПД, компактны, просты в изготовлении, неприхотливы в работе.
Достигнутые успехи в разработке и испытаниях ВОЛС позволяют считать, что они уже в ближайшее время займут значительное место в технике связи. Область их применения весьма широка – от линий внутригородской связи и бортовых комплексов до систем связи не большие расстояния с высокой информационной емкостью. На основе оптической волоконной связи могут быть созданы принципиально новые ситемы передачи информации, а также существенно улучшены и удешевлены существующие системы.
Разрабатываются ВОЛС для диапазона длин волн 0,8-1,06 мкм, где вначале были достигнуты малые потери в волокнах. Однако последние испытания показали, что наиболее обещающей областью длин волн для ВОЛС является 1,2-1,5 мкм. Здесь получены минимальные потери в волокнах и низкая дисперсия материала волокон. Однако на этих длинах волн пока отсутствуют достаточно эффективные и надежные излучатели и фотоприемники.
Широкополосные ВОЛС сделают в будущем видеотелефонную связь такой обычной, как в настоящее время обыкновенная телефонная связь.
Развитие кабельного телевидения также связанно с использованием оптических кабелей, так как только в этом случае можно обеспечить высокое качество изображения в массовых системах этого типа, рассчитанных на индивидуальных абонентов. Кабельное телевидение приведет к качественному расширению возможностей информационного обслуживания. Речь идет о передаче через абонентский телевизор изображений газетных, журнальных и книжных страниц из библиотек и специальных информационных или учебных центров.
В ВОЛС будет использоваться преобразование речевых сигналов в оптические непосредственно с помощью акустооптических преобразователей. Для передачи изображений будут применять аппаратуру с непосредственным сканированием и разложением оптического изображения и последующей передачей его без применения электронных схем. Все это дает возможность значительного упрощения оконечного оборудования системы и улучшения их технико-экономических показателей.
Типичный оптический ретранслятор или передатчик, включающий лазер, модулятор, детектор, линзы и т.д., выполненный на оптической скамье, имеет много недостатков. Традиционные оптические приборы должны быть юстированы с чрезвычайно высокой точностью, и, следовательно, они чувствительны к изменениям температуры и малейшим вибрациям раздельно установленных частей. Решение этих проблем состоит в том, чтобы объединить оптические компоненты на одной подложке, соединив их миниатюрными оптическими волноводами.
Интегральная оптика является оптическим аналогом интегральной электроники. Она дает возможность выполнить сложные оптические устройства в виде одного блока подобно интегральным схемам более низкочастотного диапазона. Она базируется на факте, что световые волны благодаря явлению полного внутреннего отражения могут распространяться в тонких пленках из прозрачных материалов, которые нанесены на подложки с коэффициентом преломления меньше, чем у пленки. Физические системы интегральной оптики отличаются от обычных оптических систем тем, что световые волны распространяются как направляемые волны внутри диэлектрических тонких пленок, а не как дифракционно ограниченные пучки в свободном пространстве. Тонкопленочные диэлектрические волноводы являются основой почти всех устройств интегральной оптики. Если оптические волноводы создать в электрооптическом материале, то фазовые скорости распространения света в световодах можно менять путем приложения электрического поля к электрооптическому материалу, приводящему к изменению его коэффициента преломления.
Так как на оптических частотах длина волны очень мала, то вся система будет очень компактной и будет иметь высокую концентрацию компонентов. Интегральные оптические системы будут потреблять незначительную мощность, обладать большой скоростью обработки информации, высокой помехозащищенностью. Иметь большую надежность, лучшую механическую и температурную стабильность.
Весьма перспективно применение лазеров для голографии, так как получение голограмм возможно только при использовании источников света, обладающих временной и пространственной когерентностью. Примером использования голограмм является и получение периодических структур для лазеров с распределенной обратной связью, изготовление амплитудно-фазовых фильтров для оптической обработки информации и т.д. Близкие к практической реализации быстродействующие голографические запоминающие устройства большой емкости, обеспечивающие хранение информации с высокой плотностью и надежное ее воспроизведение. Указывается, что на стандартной фотографической пластинке размером 9х12 см2 может быть записана информация, достигающая 108 бит.
Интересным применением голографии является цветное трехмерное телевидение.
Лазеры применяются в системах космической связи, на линиях “Спутник-Земля”, в оптической локации, в системах записи и обработки информации, в метрологии, медицине, для обработки материалов.
Ионные лазеры используются в системах подводной связи, так как в воде наилучшим образом распространяется сине-зеленый свет, который соответствует длине волны излучения аргонового лазера (l =0,5 мкм). Лазеры на СО2 являются перспективными для наземных установок, так как их излучение (l =10,6 мкм) находится в полосе прозрачности атмосферы.
Контрольные вопросы.
- Квантовые генераторы света (лазеры). Твердотельный лазер с оптической накачкой.
- Открытые оптические резонаторы и их свойства.
- Гелий-неоновый газовый лазер: устройство и принцип действия.
- Полупроводниковый инжекционный лазер: устройство и принцип действия.
- Применение лазеров в технике связи.
Список литературы
1. Андрушко Л.М., Федоров Н.Д. “Электронные и квантовые приборы СВЧ”, 1981г.
2. Лебедев И.В. “Техника и приборы СВЧ”, ч. 2, 1972 г.
3. Гасанов Л.Г. и др. “Твердотельные устройства СВЧ в технике связи”, 1988 г.
4. Гусятинер М.С., Горбачев А.Н. “Полупроводниковые сверхчастотные диоды”, 1983 г.
5. “Электронные квантовые приборы и микроэлектроника” под ред. Федорова Н.Д., 1998 г.

