Рассмотрим некоторую электрическую цепь – четырехполюсник (рис. 3.1), имеющую амплитудно-частотную характеристику (АЧХ), изображенную на рис. 3.2, а, а ослабление – на рис. 3.2, б. Пусть для упрощения входной сигнал 
состоит из суммы всего двух гармоник с частотами 
и 2
(рис. 3.3, а). Форма входного сигнала показана на этом рисунке жирной линией.
Рис. 3.1
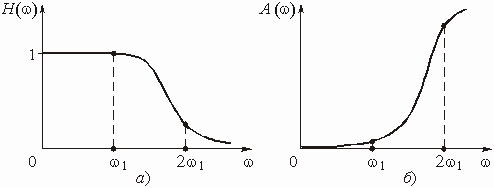
Рис. 3.2
Из анализа графиков АЧХ и ослабления цепи следует, что амплитуда первой гармоники при прохождении сигнала через цепь останется практически неизменной, а амплитуда второй гармоники уменьшится в несколько раз.
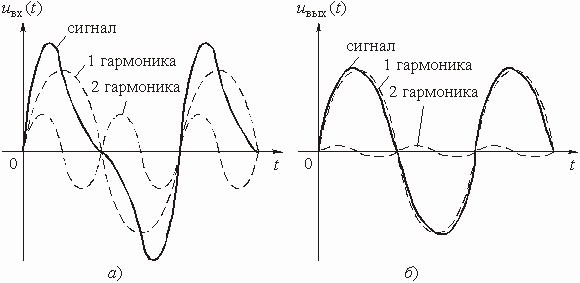
Рис. 3.3
Результат сложения гармоник на выходе цепи дает форму сигнала, отличающуюся от входной (рис. 3.3, б).
Изменение формы сигнала на выходе цепи по сравнению с формой сигнала на ее входе называется искажением сигнала. Когда искажения формы сигнала связаны с непостоянством амплитудно-частотной характеристики цепи, они носят название амплитудно-частотных искажений.
Таким образом, условием отсутствия амплитудно-частотных искажений в цепи следует считать постоянство ее АЧХ (ослабления) на всех частотах:
; 
. (3.1)
На практике условие (3.1) часто не выполняется, т. е. АЧХ и ослабление цепей аппаратуры и линий связи не являются постоянными. Эти цепи практически всегда вносят амплитудно-частотные искажения в передаваемый сигнал. Устранить подобные искажения полностью не удается, но их можно уменьшить до величин, допустимых соответствующими нормами. Для этих цепей применяются амплитудные корректоры.
Амплитудный корректор – это четырехполюсник, который включается каскадно с цепью. Его задача заключается в том, чтобы дополнить АЧХ цепи или ее рабочее ослабление до постоянной величины на всех частотах рабочего диапазона. Вне рабочего диапазона АЧХ цепи может иметь любую форму.
На рис. 3.4 изображена цепь, работающая между генератором с внутренним сопротивлением 
и нагрузкой 
. Рабочий коэффициент передачи этой цепи в соответствии с (1.3) равен
.
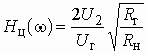Рис. 3.4
Для достижения условий безискаженной передачи между цепью и нагрузкой включен корректор (рис. 3.5). Чтобы режим работы цепи не нарушался, входное сопротивление корректора должно равняться сопротивлению нагрузки. Очевидно, только при этом условии напряжение на выходе цепи будет равно 
, как и в схеме рис. 3.4 до включения корректора.
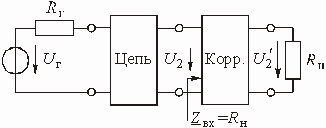
Рис. 3.5
Если обозначить напряжение на выходе каскадного соединения цепи и корректора 
, то рабочий коэффициент передачи такого соединения запишется в виде
.
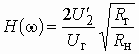Разделим и умножим это выражение на 
и представим его в виде произведения двух сомножителей
.
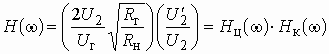Первый сомножитель представляет рабочий коэффициент передачи цепи (см. рис. 3.4), а второй – коэффициент передачи по напряжению корректора.
Ослабление, вносимое каскадным соединением цепи и корректора,
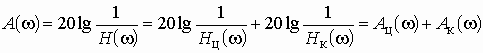
вычисляется путем сложения ослаблений цепи и корректора.
Из рис. 3.6 видно, что корректор должен вносить ослабление, дополняющее ослабление цепи в рабочей полосе частот 
до постоянной величины 
.
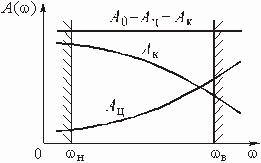
Рис. 3.6
Симметричный Т-перекрытый четырехполюсник приведен на рис. 3.7. Сопротивления 
и 
выбираются обратными, т. е. 
. Если такой четырехполюсник нагрузить на сопротивление 
, то его входное сопротивление окажется равным также .
Рис. 3.7
Комплексная передаточная функция по напряжению схемы рис. 3.7 может быть вычислена по формуле
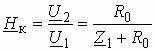или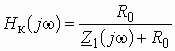 
.
Операторная передаточная функция по напряжению имеет вид:
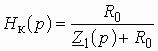. (3.2)
Вычислим ослабление, вносимое корректором:
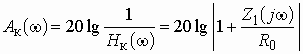. (3.3)
Данная формула показывает, что зная поведение 
на разных частотах, можно определить частотную зависимость ослабления 
.
Пример 3.1
Схема двухполюсника 
в продольном плече корректора изображена на рис. 3.8, а. Построить график частотной зависимости ослабления корректора 
.
Построим вначале график частотной зависимости сопротивления реактивного двухполюсника 
, образованного элементами 
, 
, 
и 
. На нулевой частоте индуктивное сопротивление равно нулю, а емкостное – бесконечности, поэтому 
. Двухполюсник имеет три резонанса, причем первый – резонанс напряжений, на частоте 
, второй – резонанс токов на частоте 
, третий – снова резонанс напряжений на частоте 
. Это значит, что 
, 
. При 
сопротивление также бесконечно большое (рис. 3.8, б).
Сопротивление 
, стоящее в продольном плече корректора, содержит помимо реактивных элементов активное сопротивление 
(рис. 3.8, а). Поэтому на частотах, равных 0, 
и Ґ , на которых реактивное сопротивление стремится к Ґ , полное сопротивление 
двухплюсника ограничено величиной 
(рис. 3.8, в).
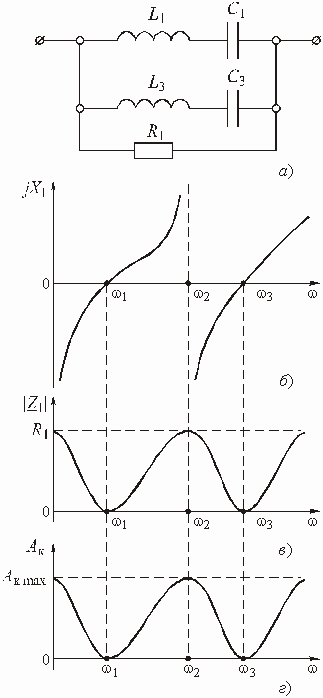
Рис. 3.8
Ослабление корректора 
рассчитывается по формуле (3.3) и зависит от значений 
. График повторяет по форме график 
. На частоте резонанса токов , а также на частотах 
и ослабление корректора достигает своего максимального значения
.
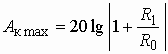На частотах резонанса напряжений 
и 
значение равно 0 (рис. 3.8, г).
Пример 3.2
Задано ослабление 
цепи, подлежащей коррекции (рис. 3.9, а). Привести схему корректора, выравнивающего характеристику этой цепи до значения 
.
Находим требуемую характеристику ослабления 
корректора из условия = – . График приведен на этом же рис. 3.9, а.
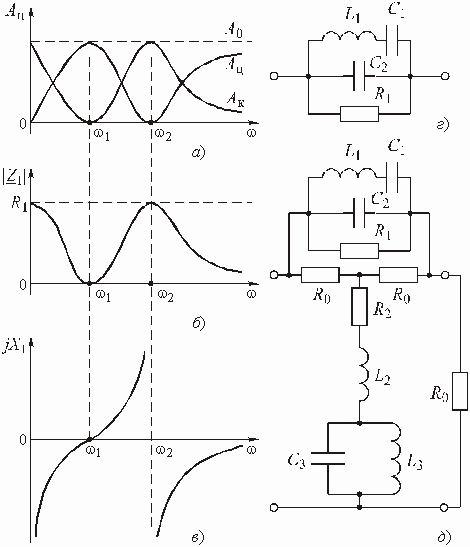
Рис. 3.9
По характеристике строим графики частотной зависимости полного сопротивления 
и реактивного сопротивления 
продольного плеча корректора (рис. 3.9, б и 3.9, в).
Из графиков рис. 3.9, в и 3.9, б следует, что двухполюсник 
имеет три реактивных элемента и одно активное сопротивление. В схеме два резонанса: первым наступает резонанс напряжений на частоте 
, вторым – резонанс токов на частоте 
. Таким условиям удовлетворяет двухполюсник , изображенный на рис. 3.9, г. Двухполюсник 
в поперечном плече корректора является обратным двухполюснику .
Схема корректора приведена на рис. 3.9, д.
Звенья 1-го порядка содержат по одному реактивному элементу в двухполюсниках и . На рис. 3.10, а изображено такое звено с двухполюсником , состоящим из параллельного соединения элементов 
и 
.
Операторное сопротивление двухполюсника :
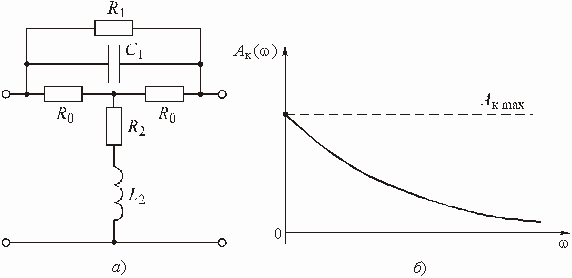
Рис. 3.10
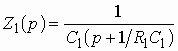. (3.4)
Если подставить выражение (3.4) в формулу (3.2), то получим операторную передаточную функцию звена:
,
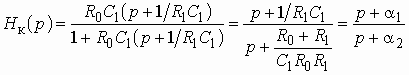где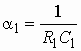 
и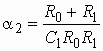 
.
Частотная характеристика ослабления данного звена
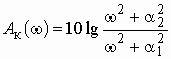; (3.5)
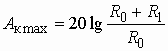
показана на рис. 3.10, б.
На рис. 3.11, а изображено звено 1-го порядка с двухполюсником 
, состоящим из параллельного соединения 
и 
. Операторная передаточная функция этого звена
,
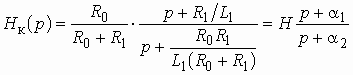где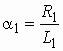 
и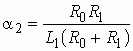 
, 
.
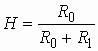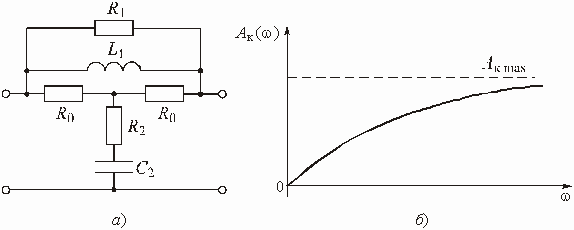
Рис. 3.11
Частотная характеристика ослабления звена
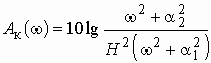
показана на рис. 3.11, б.
Максимальное значение ослабления корректора
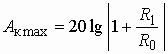. (3.6)
Звенья 2-го порядка содержат по два реактивных элемента в двухполюсниках и 
. На рис. 3.12, а изображено звено, содержащее последовательный колебательный контур и сопротивление 
в продольной ветви корректора. Операторная передаточная функция такого звена
,
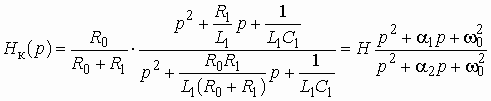где ,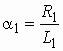 
, , 
.
Частотная характеристика ослабления звена
показана на рис. 3.12, б.
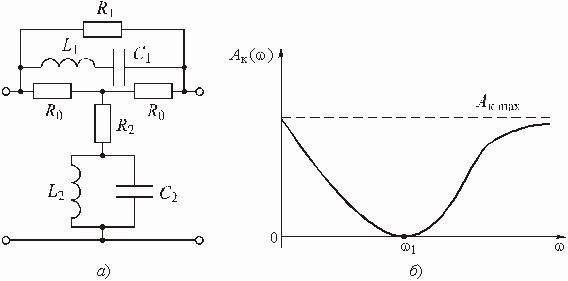
Рис. 3.12
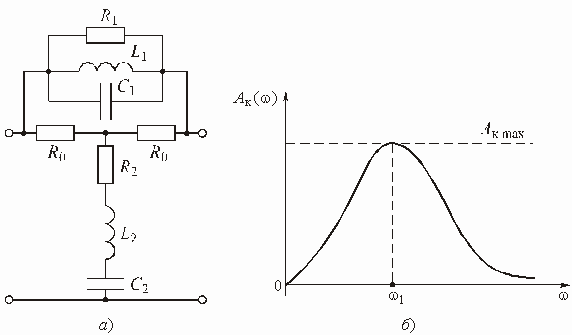
Рис. 3.13
Максимальное значение 
по-прежнему рассчитывается по формуле (3.6).
На рис. 3.13, а изображено еще одно звено 2-го порядка с двухполюсником , представляющим собой параллельный колебательный контур. Операторная передаточная функция звена и частотная характеристика ослабления (рис. 3.13, б) имеют вид
,
,
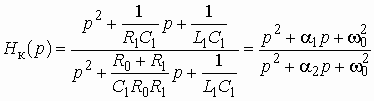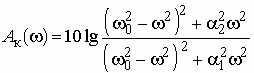где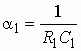 
, 
, .
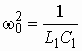Значение на графике рис. 3.12, б рассчитывается по формуле (3.6).
Пример 3.3
Определить элементы в поперечном плече корректора (рис. 3.10, а), имеющего элементы 
= 600 Ом, 
= = 2400 Ом, 
= 60 нФ. Рассчитать и построить частотную зависимость ослабления корректора 
в диапазоне частот 0 ё 8 кГц.
Элементы сопротивления 
в поперечной ветви должны быть обратны сопротивлению 
.
Из теории двухполюсников известно, что для обратных двухполюсников 
. Отсюда
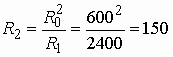Ом,
мГн.
Значения 
рассчитываем по формуле (3.5) или по общей формуле (3.3), применимой для корректора любого типа. Например, на частоте f = 0 получаем
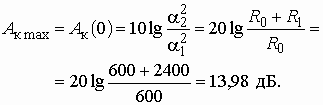
Остальные значения 
рассчитываются аналогично. По результатам расчета простроен график , изображенный на рис. 3.14.
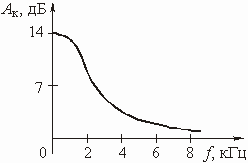
Рис. 3.14
Помимо Т-перекрытой схемы корректора (рис. 3.7) применяются также другие схемы, изображенные на рис. 3.15.
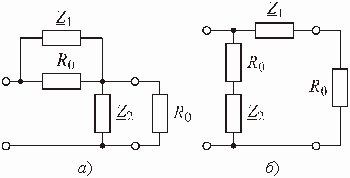
Рис. 3.15
Рис. 3.16
Передаточные функции, которые реализуются Т-перекрытым корректором, можно реализовать и элементарными четырехполюсниками, схемы которых приведены на рис. 3.16. Например, для четырехполюсника на рис. 3.16, а операторная передаточная функция
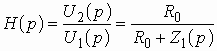
рассчитывается также, как и для корректора, построенного по Т-перекрытой схеме (см. формулу (3.2)). Цепи с элементарными четырехполюсниками применяются в случаях, когда не требуется согласование между генератором, корректором и нагрузкой.
Кроме пассивных схем амплитудных корректоров применяют активные схемы. Активные амплитудные корректоры строятся в общем случае с применением RC- и RLC-элементов, которые называют ARZ-цепями. Существует большое количество разновидностей активных звеньев эквивалентных по передаточной функции пассивным амплитудным корректорам. Две схемы таких активных звеньев изображены на рис. 3.17. Их передаточные функции выражаются соответствующими формулами (см. Примеры 1.5 и 1.4):
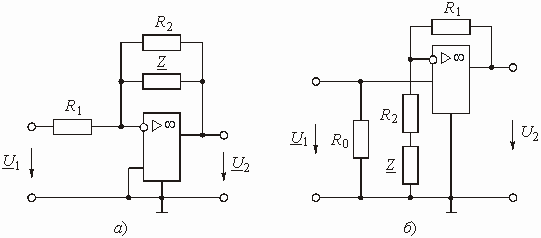
Рис. 3.17
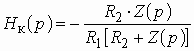, (3.7)
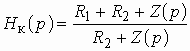. (3.8)
Если в схеме рис. 3.17, а в качестве двухполюсника Z выбрать последовательное соединение резистора R и емкости C, то передаточная функция (3.7) звена принимает вид
,
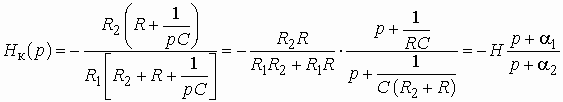где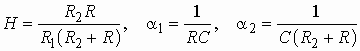 
.
Частотная характеристика ослабления данного звена, также как и у пассивного звена 1-го порядка, вычисляется по формуле
.
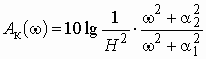Данная функция при увеличении частоты имеет монотонно возрастающий характер от величины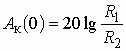 
до величины 
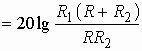. Если выбрать 
и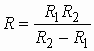 
, то ослабление будет изменяться от 
до нуля, оставаясь отрицательным (рис. 3.18, кривая 1).
Выберем в схеме 3.17, б в качестве двухполюсника Z емкость С. Тогда передаточная функция (3.8) этого звена принимает вид
,
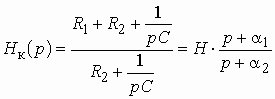где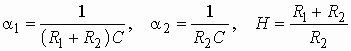 
.
Частотная характеристика ослабления
.
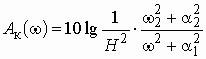При увеличении частоты данная функция имеет монотонно убывающий характер от 
до 
(рис. 3.18, кривая 2).
Если в качестве двухполюсника Z выбрать последовательный LC-контур, то частотная характеристика ослабления будет иметь вид, показанный на рис. 3.19, кривая 1. При выборе в качестве двухполюсника Z параллельного LC-контура частотная характеристика ослабления будет иметь обратный характер, как показано на рис. 3.19, кривая 2.
Рис. 3.18 Рис. 3.19
Несмотря на то, что рассмотренные схемы могут содержать индуктивности, они имеют ряд преимуществ по сравнению с пассивными амплитудными корректорами. Так, число реактивных элементов вдвое меньше, а ослабление, вносимое каскадным соединением цепи и корректора, близко к нулю. Последнее важно также потому, что дополнительное ослабление за счет применения пассивного корректора, как правило, приходится компенсировать с помощью усилителя, т. е. общая схема все равно оказывается активной.
Пример 3.4
Определить передаточную функцию амплитудного корректора, построенного по схеме рис. 3.17, б, в которой в качестве двухполюсника Z выбран последовательный колебательный LC-контур. Рассчитать и построить частотную характеристику ослабления 
корректора в диапазоне частот от 0 до 
= 100 кГц для элементов контура 
= 10 кОм, 
= 20 кОм, L = 200 мГн, С = 1,268 нФ.
Операционный усилитель в схеме рис. 3.17, б включен по неинвертирующей схеме, поэтому передаточная функция корректора определяется по формуле (3.8), в которой 
:
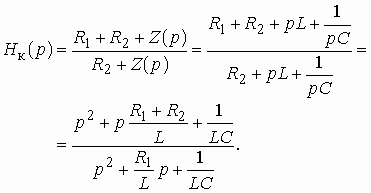
Частотная характеристика ослабления
.
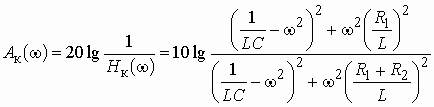В формулах 
и 
величина 
– это квадрат резонансной частоты 
LC-контура. Для заданных значений L и С имеем
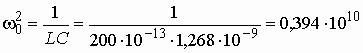(рад/с)2.
Резонансная частота 
= 10 кГц. Рассчитаем значения 
на частотах, равных нулю, 
= 10 кГц и 
= 100 кГц.
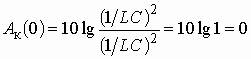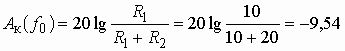дБ,
дБ,
дБ.
Аналогичным образом можно рассчитать ослабление на любой частоте в рабочем диапазоне. График изображен на рис. 3.20.
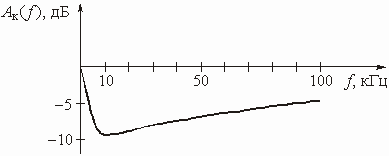
Рис. 3.20
При расчете пассивного амплитудного корректора исходными данными являются: частотная характеристика ослабления цепи 
, подлежащая коррекции в диапазоне частот 
... 
; точность коррекции D A в этом же диапазоне частот; сопротивление нагрузки 
.
Вначале определяют частотную характеристику амплитудного корректора 
. Для этого необходимо задать характеристику ослабления 
каскадного соединения цепи и корректора. Эта характеристика должна быть постоянной, не зависящей от частоты, причем ее величину принимают несколько большей, чем максимальное ослабление цепи:
, (3.9)
где 
= 1 ... 2 дБ.
Частотная характеристика ослабления амплитудного корректора вычисляется по формуле
. (3.10)
На рис. 3.6 в качестве примера показаны характеристики ослабления цепи 
, ослабления каскадного соединения цепи и корректора, а также ослабления корректора.
Следующим этапом расчета амплитудного корректора является выбор схемы корректора. Выбирают такую схему, которая в диапазоне частот ... имеет нужный характер частотной зависимости ослабления. Например, для реализации частотной зависимости , приведенной на рис. 3.6, можно использовать амплитудный корректор, в котором двухполюсник 
состоит из параллельного соединения емкости 
и резистора 
(рис. 3.10).
Выбрав схему корректора, приступают к ее расчету. При этом часто используется метод интерполирования. Согласно этому методу задаемся числом точек интерполирования, равным числу элементов в двухполюснике . С учетом формулы (3.3) составляется система уравнений вида
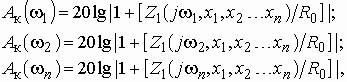
где 
значения параметров элементов двухполюсника . Решение данной системы и дает значения 
, которые являются параметрами индуктивностей, емкостей и резисторов.
Особенностями расчета является то, что во-первых, параметры элементов могут быть отрицательными, а во-вторых – точность коррекции может не удовлетворять заданным требованиям. Обычно приходится данный расчет повторять. Если параметры элементов получились отрицательными, то следует либо изменить величину 
в формуле (3.9), либо положение точек интерполяции. Если параметры элементов получились в конце концов положительными, то проверяется точность аппроксимации (коррекции). Для этого по формуле (3.3) рассчитывается ослабление корректора 
и проверяется выполнение неравенства
Ф D А.
При выполнении неравенства расчет на этом заканчивается. В противном случае необходимо снова повторить расчет, меняя точки интерполяции, до получения равноволновой характеристики погрешности. Если при равноволновом характере погрешности требования к точности не выполняются, то необходимо либо увеличить число элементов в двухполюснике, либо поделить 
пополам и построить корректор в виде каскадного соединения двух четырехполюсников.
Методика синтеза активных ARZ-корректоров такая же, как и описанная выше методика расчета пассивных амплитудных корректоров. Отличие заключается в том, что характеристика ослабления 
каскадного соединения цепи и корректора выбирается близкой к нулю.
Пример 3.5
В таблице 3.1 задана частотная характеристика ослабления цепи 
. Рассчитать элементы амплитудного корректора, если 
= 12 дБ и 
= 200 Ом.
Воспользуемся формулой (3.10) и рассчитаем ослабление корректора 
в диапазоне частот от 0 до 50 кГц.
Таблица 3.1
|
f, кГц |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
|
0,1 |
1,0 |
2,0 |
3,5 |
4,8 |
6,2 |
7,7 |
8,6 |
9,5 |
10,2 |
10,9 |
, дБ
Результаты расчета 
приведены в таблице 3.2, а на рисунке 3.21 изображены графики ослаблений , и .
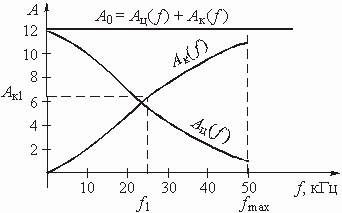
Рис. 3.21
Таблица 3.2
|
f, кГц |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
|
11,9 |
11,0 |
10,0 |
8,5 |
7,2 |
5,8 |
4,3 |
3,4 |
2,5 |
1,8 |
1,1 |
, дБ
Частотная характеристика ослабления на рис. 3.21 может быть получена с помощью корректора, реализованного по схеме рис. 3.11, в которой двухполюсник 
состоит из параллельного соединения элементов 
и 
.
Найдем из формулы (3.6):
.
Значение 
= 10,9 дБ на частоте f = 50 кГц берем из таблицы 3.2. Получаем
= 500 Ом.
Для расчета выбираем узел интерполяции: 
= 25 кГц, 
= 6,2 дБ. Подставляем эти данные в формулу (3.3) или
,
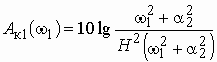где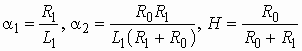 
, 
.
Получаем значение 
= 2 мГн.
Значения параметров элементов 
и 
, образующих обратный двухполюсник 
, рассчитываем по формулам
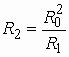и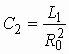 
.
Получаем = 80 Ом и = 0,05 мкФ. Расчетная характеристика ослабления корректора, вычисляемая по формуле (3.3), точно совпадает с требуемой только на частотах = 25 кГц и 
= 50 кГц.
Используя каскадное соединение различных типовых звеньев корректоров, можно получить частотные зависимости ослабления 
любой сложности. На рис. 3.22 изображена схема сложного корректора, построенного на основе типовых схем (рис. 3.13), и его рабочее ослабление. Изменением характеристик типовых схем добиваются получения требуемой характеристики амплитудного корректора.
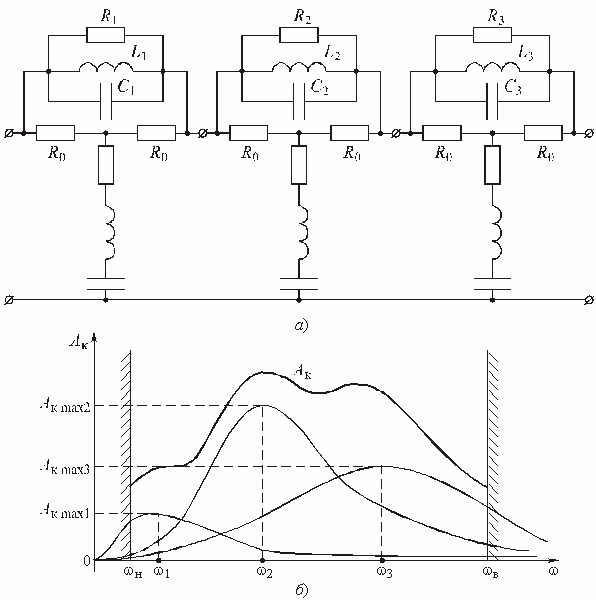
Рис. 3.22
Вопросы и задания для самопроверки
1. Почему происходят искажения сигнала на выходе цепи?
2. Сформулировать условие отсутствия амплитудно-частотных искажений в цепи.
3. Каким образом корректируются частотные характеристики цепей?
4. По какой схеме можно построить пассивный амплитудный корректор?
5. Как рассчитывается передаточная функция Т-перекрытого корректора и вносимое им ослабление?
6. Схема двухполюсника 
в корректоре приведена на рис. 3.8, а. Получить схему двухполюсника 
. Построить график частотной зависимости ослабления 
корректора.
7. Какие схемы типовых звеньев пассивных корректоров известны? Какой вид имеют частотные характеристики вносимого ими ослабления?
8. Доказать, что частотная характеристика ослабления 
звена, изображенного на рис. 3.10, имеет вид (3.5), а максимальное значение ослабления рассчитывается по формуле 
.
9. Доказать, что операторная передаточная функция элементарного четырехполюсника, изображенного на рис. 3.16, б, соответствует передаточной функции корректора (формула (3.2)).
10. Какие амплитудные корректоры называются активными?
11. Получить передаточную функцию и частотную характеристику ослабления активного звена корректора, изображенного на рис. 3.17, б, в котором в качестве двухполюсника Z выбран параллельный LC-контур. Подтвердить, что график рабочего ослабления 
такого корректора – это кривая 2 на рис. 3.19.
Ответ: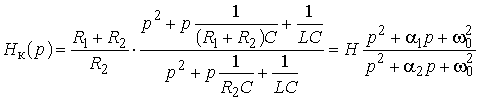 
.
12. Каков порядок расчета пассивного амплитудного корректора? 13. Рассчитать элементы, образующие двухполюсник 
амплитудного корректора, частотная зависимость ослабления 
которого приведена в таблице 3.3, а значение 
= 200 Ом.
Таблица 3.3
| f, кГц | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
 , дБ |
15,6 | 10,5 | 6,3 | 4,0 | 2,7 | 1,9 | 1,4 | 1,1 | 0,9 | 0,7 | 0,6 |
Ответ: 
= 1 кОм, 
= 51 нФ. 14. Зачем применяют каскадное соединение типовых звеньев корректоров?