2.4.2. Взаимодействие оптической волны со средой
2.4.1. Основные понятия
Строгое решение задач распространения электромагнитной энергии по оптическим кабелям требует применения классической электродинамики и уравнений Максвелла. На основе электродинамики можно рассмотреть практически все вопросы передачи, излучения, влияния и поглощения в ОК. Правда, во многих случаях очень сложно искать точные решения на базе электродинамики. Для практики в свое время были разработаны приближенные методы решения задач различных классов. Таким наиболее характерным методом является метод теории геометрической оптики, когда (квазиоптический режим) совершается переход от волновых электродинамических процессов к лучевым процессам (λ→0). При λ→0 области очень высоких частот (свыше 1013 Гц) справедливы уравнения геометрической оптики. Однако квазиоптический режим передачи по ОВ является предельным случаем строгих уравнений электродинамики.
Носителем электромагнитной энергии, широко используемой в современной радиоэлектронике, электросвязи и высоковольтной технике, является электромагнитное поле. Электромагнитное поле — это особый вид материи, оказывающий силовое воздействие на заряженные частицы и обладающий энергией, массой, скоростью, т.е. всеми свойствами материи. Поле отличается непрерывным распределением в пространстве (электромагнитные волны) и обнаруживает дискретность структуры (фотоны). Электромагнитное поле представляет собой единство двух составляющих — электрического и магнитного полей. Электрическое поле (Е) характеризуется силовым взаимодействием как с неподвижными, так и с движущимися зарядами. Магнитное поле (Н) характеризуется силовым взаимодействием лишь с движущимися зарядами. Электрические и магнитные поля связаны с определенными количествами электромагнитной энергии. В различных случаях может преобладать тот или иной вид энергии (электрической или магнитной).
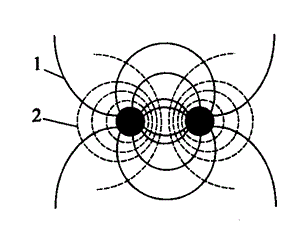
Рис. 2.17. Линии полей: 1-потенциальные; 2-вихревые
Различают два основных типа полей: потенциальное и вихревое. Потенциальное поле тесно связано со своим источником. Линии поля имеют начало и конец. Линии вихревого поля замыкаются по соленоиду, всегда непрерывны и не имеют начала и конца (рис. 2.17). Электростатическое поле является чисто потенциальным, а магнитное — чисто вихревым. Переменное электромагнитное поле в общем случае является суперпозицией потенциального поля электрических зарядов и вихревого поля индукции.
Электрические и магнитные свойства среды характеризуются тремя параметрами: диэлектрической проницаемостью (ε), магнитной проницаемостью (μ) и электрической проводимостью (σ).
Оптическая мощность сигнала, передаваемая по ОВ, описывается векторами напряженности (E ) и индукции (D ) электрического поля, а также векторами напряженности (Н) и индукции (В) магнитного поля. Последние связаны между собой и параметрами среды распространения следующими уравнениями Максвелла, при условии, что проводимость среды σ = 0:
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
![]() (2.21)
(2.21)
Диэлектрическая и магнитная проницаемости описывают материалы, используемые в ВОСП, которые могут быть линейными и нелинейными, изотропными и анизотропными, однородными и неоднородными, дисперсионными и недисперсионными. У абсолютного большинства материалов, используемых в ВОСП, μ=μ0 - магнитная проницаемость вакуума.
В зависимости от свойств параметров ε, μ и σ различают следующие среды:
- линейные, в которых параметры ε, μ и σ не зависят от величины электрического и магнитного полей;
- нелинейные, в которых параметры ε, μ и σ (или хотя бы один из них) зависят от величины электрического или магнитного полей.
Все реальные среды, по существу, являются нелинейными. Однако при не очень сильных полях во многих случаях можно пренебречь зависимостью с, и и ч от величины электрического и магнитного полей и считать, что рассматриваемая среда линейна.(В дальнейшем будут рассматриваться только линейные среды.) Линейные среды делятся на однородные и неоднородные, изотропные и анизотропные.
Однородными называют среды, параметры ε, μ и σ которых не зависят от координат, т.е. свойства среды одинаковы во всех ее точках. Среды, у которых хотя бы один из параметров ε, μ или σ является функцией координат, называют неоднородными. Несмотря на то, что кварц является однородной средой, оптическое волокно неоднородно из-за того, что показатели преломления сердцевины и оболочки различны. Поэтому области сердцевины и оболочки в волокне со ступенчато изменяющимся показателем преломления могут рассматриваться раздельно как однородные среды, в то время как в градиентном волокне это допущение неприемлемо, ввиду его неоднородной сердцевины.
Если свойства среды одинаковы по разным направлениям, то среду называют изотропной. Соответственно среды, свойства которых различны по разным направлениям, называют анизотропными. В изотропных средах вектор электрической поляризации ( р) и вектор (E), векторы (D) и (Е), а также векторы магнитной поляризации (М) и (Н), векторы (В ) и (Н ) параллельны, в анизотропных средах они могут быть непараллельными. В изотропных средах параметры ε, μ и σ — скалярные величины. В анизотропных средах, по крайней мере, один из этих параметров является тензором.
В кристаллическом диэлектрике тензором является диэлектрическая проницаемость ε. В общем случае ее записывают в виде матрицы:
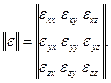
![]() (2.22)
(2.22)
При этом форма уравнения (2.18) остается прежней:
![]() (2.23)
(2.23)
Для того чтобы записать уравнение (2.23) в проекциях на оси прямоугольной системы координат х, у, z, нужно раскрыть правую часть уравнения (2.23) по обычным правилам умножения матрицы. В результате получим
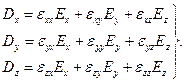 (2.24)
(2.24)
Непараллельность векторов D и Е (а также р и Е) в анизотропной среде объясняется тем, что в общем случае направление возникающего в результате поляризации анизотропной среды вторичного электрического поля, созданного связанными зарядами вещества, составляет некоторый угол (отличной от 0 и π) с направлением первичного электрического поля.
Таким образом, в изотропной среде электромагнитные свойства, такие как показатель преломления, одинаковы во всех направлениях, а Е и р являются векторами одинаковой ориентации, и так как кварц представляет собой изотропную среду, идеально цилиндрическое оптическое волокно также является изотропным.
Среда, показатели преломления которой вдоль двух разных направлений соответствующей системы координат, например вдоль осей х и у, различны, называется двулучепреломляющей, поэтому оптическое волокно, не обладающее цилиндрической системой, также является двулучепреломляющим. Двулучепреломление ряда материалов, например ниобата лития, используется в таких волоконно-оптических компонентах, как модуляторы, изоляторы и настраиваемые фильтры.
Среда, в которой ε=const, т.е. однородная по координатам пространства и не зависящая от частоты, называется однородной недисперсионной средой. В ней все частотные составляющие сигнала распространяются с одной и той же фазовой скоростью. Следовательно, сигнал не претерпевает дисперсии. Большинство оптических сред характеризуется тем, что ε = ε (ω) и ν= ν(ω) являются функциями от частоты. Это значит, что косинусоидальные волны
![]() (2.25)
(2.25)
разных частот распространяются с различными фазовыми скоростями, что приводит к расширению сигнала, т.е. к появлению дисперсии.
В выражении (2.25): А — амплитуда волны; ω — круговая частота; n — единичный вектор, нормальный к плоскости, в которой находится плоская волна; r — координата точки наблюдения.
2.4.2. Взаимодействие оптической волны со средой
До сих пор мы говорили о средах без учета распространения в них света, представляющего собой электромагнитную волну. Что происходит, когда оптическая волна распространяется в изотропной среде (материале)?
Как известно, электроны в атоме заряжены отрицательно, а ядро несет положительный заряд. Электрическое поле синусоидальной оптической волны, распространяющейся через материал, воздействует на него. Под действием силы внешнего электрического поля в материале изменяются колебания заряженных частиц атома. В результате такого взаимодействия мощность световой волны уменьшается, т.е. происходит поглощение света. Колеблющиеся заряды атома переизлучают полученную от световой волны мощность на собственных частотах ω0. Таким образом, синусоидальная оптическая волна частотой в создает систему осцилляторов (диполей). Средняя во времени излучаемая осциллятором мощность в соответствии с законом Рэлея [7] представляется в виде:
![]() (2.26)
(2.26)
где q — заряд частицы, колеблющейся по синусоидальному закону с частотой ω, с — скорость света в вакууме; ε — диэлектрическая проницаемость среды (материала); ![]()
Комплексная амплитуда вынужденных колебаний частицы с частотой ω
![]() (2.27)
(2.27)
где m, a, ω0 — соответственно масса покоя, коэффициент «трения» и резонансная частота частицы.
Поэтому при взаимодействии оптического поля со средой возникают электрические диполь. На микроскопическом уровне плотность дипольных моментов характеризуется вектором поляризации среды. Если в единице объема имеется N одинаковых атомов, каждый из которых содержит, например, η электронов, то вектор поляризации
![]() (2.28)
(2.28)
Таким образом, индуцированная электрическая поляризация материала, или просто поляризация, может быть описана при помощи вектора р, который зависит как от особенностей материала, так и от прилагаемого поля. Индуцированная поляризация рассматривается как отклик среды на прилагаемое электрическое поле. Рассмотрим связь р и Е более подробно, определив вначале вектор D, называемый электрической индукцией:
![]() (2.29)
(2.29)
где εст — постоянная, называемая статической диэлектрической проницаемостью среды, в нашем случае ОВ.
Исходя из (2.28) и (2.29), комплексную диэлектрическую проницаемость можно представить в виде суммы статической и динамической составляющих:
![]() (2.30)
(2.30)
Откуда
![]() (2.31)
(2.31)
Для чистого стекла (плавленого кварца без примесей, химическая формула которого SiO2) резонансная частота электрона ω0 расположена в ультрафиолетовой области спектра.
Следовательно, в видимой и ближней инфракрасной областях спектра (ω<<ω0) диэлектрическая проницаемость практически постоянна:
![]() (2.32)
(2.32)
В реальных стеклах, кроме атомов Si и О, в единице объема содержатся и ионы примесей (ионы — ОН, Fe, Cu, Cr и др.), а также молекулы. Таким образом, для реального стекла в выражение (2.31) необходимо добавить столько членов вида второго члена, сколько имеется диполей, обусловленных примесями. Молекула массивна, поэтому ее ω0 находится вне спектра частот, используемого в ВОСП. Связь р и E в оптическом волокне определяется свойствами среды (кварца) и является причиной двух важных явлений, относящихся к распространению в нем света, — дисперсии и нелинейным эффектам, которые налагают ограничения на функционирование современных систем ВОСП.
2.4.3. Волновые уравнения
Для математического анализа распространения электромагнитных волн в диэлектрических волноводах (оптических волокнах) методом волновой оптики необходимо воспользоваться уравнениями Максвелла (2.16) — (2.21). Из этих уравнений можно получить более удобное для практики уравнение, взяв операцию ротора от уравнения (2.17) с учетом (2.19),
![]() (2.33)
(2.33)
Подставив (2.16) и (2.18) в (2.33), получим уравнение, содержащее только один вектор Е:
![]() (2.34)
(2.34)
Это уравнение справедливо и в том случае, когда ε изменяется в пространстве, т.е. для неоднородной среды. Первый член выражения (2.34), исходя из векторной алгебры, можно представить в виде:
![]() , (2.35)
, (2.35)
где ![]() — оператор Лапласа.
— оператор Лапласа.
Заменив в этом уравнении вектор Е на D/ε, можно получить выражение первого члена правой части в виде:
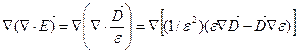 . (2.36)
. (2.36)
Поскольку ![]() то
то
![]() (2.37)
(2.37)
Тогда с учетом (2.35), (2.36) и (2.37) уравнение (2.34) принимает вид:
![]() (2.38)
(2.38)
Аналогично можно получить волновое уравнение для вектора Н, взяв операцию ротора от уравнения (2.16),
![]() (2.39)
(2.39)
Рассмотрим решение уравнения (2.38) в разных средах.
В частном случае, когда среда однородна по координатам пространства ε=const и не зависит от частоты, уравнение (2.38) принимает вид:
![]() (2.40)
(2.40)
Такой же вид в данной среде принимает и уравнение (2.39). Уравнение (2.40) справедливо для любой компоненты поля в декартовой системе координат. В цилиндрической системе координат оно справедливо только для составляющей Ez. Величина ![]() имеет физический смысл скорости в среде с диэлектрической и магнитной проницаемостями ε/ε0 и μ/μ0, где ε0, μ0 — диэлектрическая и магнитная проницаемости вакуума. Как отмечалось ранее, в оптических средах везде считается, что μ/μ0=1.
имеет физический смысл скорости в среде с диэлектрической и магнитной проницаемостями ε/ε0 и μ/μ0, где ε0, μ0 — диэлектрическая и магнитная проницаемости вакуума. Как отмечалось ранее, в оптических средах везде считается, что μ/μ0=1.
Решение уравнения (2.40) может удовлетворяться любой функцией [8]:
![]() , (2.41)
, (2.41)
если существует вторая производная от ψ. Это решение представляет плоскую волну. В выражении (2.41) компоненты r являются координатами точки наблюдения, n — единичный вектор, номальный к плоскости, а v не зависит от частоты. Действительно, при фиксированном значении времени t и заданном значении аргумента этой функции
![]() (2.42)
(2.42)
функция ψ (u) имеет соответствующее фиксированное значение. Поэтому ψ (u) имеет одно и то же значение на этой бесконечной плоскости. Каждому приращению Δt соответствует приращение Δr, так что величина (2.42) остается неизменной, т.е.
![]() . (2.43)
. (2.43)
Вектор n является нормалью как к первоначальной, так и к смещенной плоскости. Из (2.42) следует, что плоскость движется в пространстве со скоростью v. Частным случаем являются такие решения уравнения (2.40), которые в каждой точке пространства изменяются во времени по косинусоиде
![]() . (2.44)
. (2.44)
Вектор ![]() называется волновым вектором. Все частотные составляющие сигнала распространяются с одной и той же фазовой скоростью. Следовательно, сигнал не претерпевает дисперсии.
называется волновым вектором. Все частотные составляющие сигнала распространяются с одной и той же фазовой скоростью. Следовательно, сигнал не претерпевает дисперсии.
В однородной дисперсионной среде при ε=ε(ω) и v=v(ω) решение (2.41) является приближенным, если дисперсия слабо выражена. В компонентах ВОСП это условие обычно выполняется.
Рассмотрим два случая: возбуждение сигнала ψ(t) некоторой светящейся плоскостью и некоторой светящейся поверхностью неплоской структуры.
Пример первый. Если некоторый сигнал ψ(t) возбуждается некоторой светящейся плоскостью, на которой этот сигнал можно представить в виде суперпозиции синусоидальных колебаний с помощью преобразования Фурье, то каждое гармоническое колебание (2.44) распространяется через дисперсионную среду как плоская волна. Такого типа волну ψ(t) можно представить в виде комплексного интеграла Фурье, располагая систему координат для удобства таким образом, чтобы она распространялась вдоль оси z. Тогда
![]() (2.45)
(2.45)
Амплитудная функция φ(ω) определяется через известную форму сигнала при z=0:
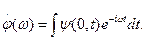 (2.46)
(2.46)
Таким образом, сигнал в пространстве дисперсионной среды представляется совокупностью волн, каждая из которых находится в своей плоскости и движется со своей скоростью.
Пространственная длительность сигнала (Δz), представленная на рис. 2.18, определяется расстоянием между плоскостью 1 с гармоническим колебанием сигнала частотой и плоскостью N с гармоническим колебанием ω2.
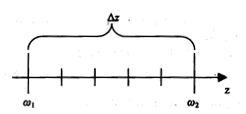
Рис. 2.18. Пространственная длительность сигнала, ?z в однородной дисперсионной среде
Напомним, что эти представления пригодны для случая, когда v слабо зависит от частоты или функция ψ(z,t) описывается узким спектром частот по сравнению с оптической несущей. Последнее условие в ВОСП также выполняется.
Фазовая скорость не имеет смысла для функции (2.45), однако эта функция правильно описывает распространение плоской волны общего вида в дисперсионной среде.
Изложенные выше представления полей, распространяющихся в дисперсионной среде, можно использовать и в случае возбуждения сигнала ψ(t) некоторой светящейся поверхностью неплоской структуры.
Пример второй. Криволинейную поверхность представим в виде совокупности плоских волн. На выходе реальных источников излучения, которыми являются лазеры, колебания сферические. Поэтому на малом расстоянии от лазера излучение представляется совокупностью плоских волн.
Используя суперпозицию плоских синусоидальных волн со всевозможными частотами, бегущих во всевозможных направлениях, можно составить общее выражение для волны, распространяющейся в дисперсионной среде:
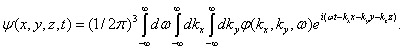 (247)
(247)
Здесь kz или любая другая составляющая волнового вектора должна удовлетворять условию:
![]() . (2.48)
. (2.48)
Составляющая kz, может быть мнимой, когда подкоренное выражение отрицательно. В этом случае вместо плоской волны имеем дело с нераспространяющейся (локальной) волной. Такие волны также являются решениями волнового уравнения (2.40).
Интегральное представление (2.47) более общей волны состоит из плоских волн всевозможных направлений распространения и всевозможных частот, а также и из нераспространяющихся (локальных) волн. При гармоническом (синусоидальном) сигнале интегрирование по частоте можно исключить.
2.4.4. Граничные условия
Уравнения Максвелла в дифференциальной форме (2.16), (2.17) справедливы для линейных сред, параметр ε которых либо не зависит от координат, либо является непрерывной функцией координат. На практике, часто рассматриваемая область состоит из двух (или более) разнородных сред. При анализе макроскопических свойств поля в этих случаях обычно приходится считать, что параметр ε на границе раздела сред меняется скачком. Операция дифференцирования в точках, принадлежащих границе раздела, незаконна, и уравнения Максвелла в дифференциальной форме в этих точках теряют смысл. Поэтому для изучения поведения векторов электромагнитного поля при переходе из одной среды в другую нужно исходить из уравнений Максвелла в интегральной форме, которые остаются справедливыми и в этих случаях. Соотношения, показывающие связь между значениями векторов электромагнитного поля в разных средах у поверхности раздела, называются граничными условиями. Уравнения Максвелла не определяют электромагнитное поле полностью без задания граничных условий.
В задачах о неоднородных структурах без скачкообразного изменения граничным условием обычно является требование исчезновения поля в бесконечности и ограниченность поля внутри любой конечной области пространства. Требование отсутствия поля в бесконечности приводит к направляемым модам (типам волн), поле которых ограничено направляющей структурой (системой), при этом не теряется их мощность на излучение.
Наиболее общий тип граничных условий в световодных устройствах соответствует кусочно-однородному распределению ε. Представляют интерес граничные условия для переменных во времени полей. Искомые граничные условия получаются из уравнений Максвелла путем интегрирования их по объему, выбираемому на границе раздела сред. Стягивая объем в точку, в пределе получаем равенство тангенциальных составляющих электрического и магнитного полей на границе раздела сред:
Нt1=Ht2, Et1=Et2 (2.49)
Физический смысл этих соотношений состоит в том, что тангенцианальные составляющие полей Н и Е непрерывны на границе раздела сред. Граничные условия совместно с условиями на бесконечности определяют конкретные решения уравнений Максвелла для конкретной задачи. При этом поля представляются в виде некоторых функций координат, частот и времени. В этом состоит волновой метод решения задач.
2.4.5. Волновой анализ распространения мод
Проведем волновой анализ распространения мод на примере ОВ со ступенчатым ППП. Для этого рассмотрим ОВ без потерь двухслойной конструкции (рис. 2.19).
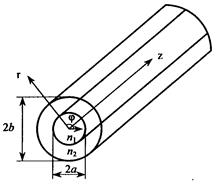
Рис. 2.19. Конструкция ОВ двухслойной структуры
Лучевой метод расчета волоконных световодов не дает полной картины распространения волн в ступенчатом ОВ. Поэтому необходимо обращаться и к волновому методу решения уравнений Максвелла или волнового уравнения.
Волновое уравнение (2.40) в цилиндрической системе координат r, φ, z относительно компонентов электрического поля или магнитного поля Нz изменяющихся во времени t и вдоль оси z волокна, в виде
![]() (2.50)
(2.50)
переходит в уравнение Гельмгольца:
![]() (2.51)
(2.51)
где 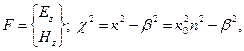 (2.52)
(2.52)
χ - поперечное волновое число, или собственное значение; β— фазовая постоянная.
Для описания поведения электромагнитного поля в сердцевине (0<r<a) и в оболочке (а<r<b) необходимо использовать различные функции. Исходя из физической сущности процессов, функции сердцевины при r = 0 должны быть конечными, а в оболочке должны описывать спадающее поле. Используем цилиндрическую систему координат, ось которой совместима с осью цилиндра. Поверхностные составляющие напряженности электрического и магнитного полей могут быть выражены через продольные составляющие Еz и Нz. Для простоты решения уравнения (2.51) предположим, что оболочка ОВ с n2 на рис. 2.19 простирается до бесконечности (d=∞). Такое упрощение модели является оправданным и приводит к адекватным характеристикам мод реального ступенчатого ОВ, имеющего защитное покрытие, обеспечивающее механическую защиту ОВ. В таком случае n в формуле (2.52) равно или n1 в середине ОВ, или п2 во внешней среде. Для нахождения бегущих вдоль оси z волн необходимо для внешней среды положить
![]() (2.53)
(2.53)
чтобы поле в радиальном направлении в среде п2 убывало. Тогда решение уравнения (2.51) можно записать:
для сердцевины ОВ с показателем преломления n1 в виде:
![]() (2.54)
(2.54)
![]() (2.55)
(2.55)
Зависимость всех полей от координат φ в виде cosnφ и sinnφ свидетельствует о том, что в волокнах круглого сечения моды на равных могут существовать в виде двух взаимно ортогональных поляризаций. Это значит, что моды в ступенчатом ОВ являются попарно вырожденными по поляризации, что особенно важно для передачи сигналов в одномодовом ОВ. Таким образом, решения (2.54) и (2.55) дают возможность изучить условия распространения волн в ступенчатом ОВ. В решениях (2.54) и (2.55) Аm, Вm, Сm и Dm — постоянные интегрирования; Jn, Nn — функции Бесселя первого и второго рода n-го порядка, соответственно; In и Kn –видоизмененные (модифицированные) функции Бесселя первого и второго рода п-го порядка, соответственно. Качественные характеристики функции в зависимости от собственных значений χ1r и a2r приведены на рис. 2.20.
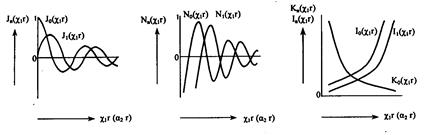
Рис. 2.20. Качественные зависимости функций Jn (χ1r),
Nn(χ1r), In(χ1r) и Kn(χ1r) от аргумента χ1r(а2r)
При r→0 значение Nn →-∞. Но так как поле на оси сердцевины не может приобретать бесконечные значения, то необходимо положить Вm =0. Поле за пределами сердцевины должно убывать в радиальном направлении и при r→∞ должно стремиться к нулю. Однако In при этом стремится к бесконечности, что противоречит условию Зоммерфельда. Следовательно, надо положить Cm = 0, так как нас интересуют только направляемые моды вдоль оси z. Таким образом, функция Jn(χ1r) описывает распределение поля внутри сердцевины ОВ, а функция Kn(а2r) описывает изменение поля за ее пределами (в среде с п2) и ведет себя при больших значениях а2r как exp( - а2r). Тогда уравнения (2.54) и (2.55) перепишутся в виде:
![]() (2.56)
(2.56)
![]() (2.57)
(2.57)
Постоянные интегрирования Ат и Dт могут быть определены на основании граничных условий, как отмечалось ранее. Поперечные составляющие электрических (Еr, Еφ) и магнитных (Нr, Нφ)полей могут быть выражены с помощью известных соотношений между поперечными и продольными (Еz, Нz) составляющими. Тогда, используя условие равенства тангенцианальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердцевина — оболочка (при r =a):
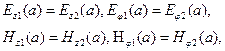 (2.58)
(2.58)
найдем постоянные интегрирования. Подставим их в уравнения типа (2.56) и (2.57), и после соответствующих преобразований получим следующее характеристическое уравнение:
![]() (2.59)
(2.59)
Это уравнение позволяет определить структуру поля, параметры волн и характеристики ОВ. В общем случае оно имеет ряд решений, каждому из которых соответствует определенная структура поля, называемая типом волны, или модой. Обычно в ступенчатых ОВ, применяемых для линий передачи сигналов, n1≈n2. Тогда уравнение (2.59) можно переписать в виде:
![]() (2.60)
(2.60)
В ступенчатом ОВ отсечка моды (критические условия) наступает при равенстве поперечного волнового числа в оболочке -α2=0, это возможно при β=k2. При этом условии из (2.60) следует, что
![]() (2.61)
(2.61)
Отсюда видно, что низшая (основная) мода (п=0) имеет отсечку, определяемую из уравнения:
![]()
Первый корень этого характеристического уравнения χ1а= 0, и он соответствует моде НЕ11. В соответствии с решением (2.54) и (2.55) эта волна существует в виде двух взаимных ортогональных поляризаций НЕ11r и НЕ11B соответствующих cosφ и sinφ (рис. 2.21). Распределение плотности поперечного поля в поперечном сечении сердцевины подчиняется закону J0(χ1r), приближающемуся к Гауссовому закону exp(–r2/ω02) распределения поля в лазерном световом пучке. Вторая в порядке возбуждения мода для n=0 отсекается, когда функция J1(χ1r) второй раз становится равной нулю, т.е. когда χ1а= 3,83 (рис. 2.22). Эта мода обозначается НЕ12. Аналогично для n=0 следуют моды НЕ13, НЕ14…
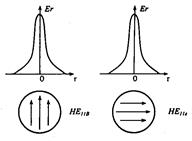
Рис. 2.21. Пример двух взаимноортогональных поляризаций моды НЕ11
В приведенных обозначениях мод первый индекс учитывает порядок функции, второй—номер корня (порядок решения), удовлетворяющего граничным условиям для данного порядка функции Бесселя.
Следующая совокупность мод соответствует n=1 или характеристическому уравнению:
![]()
![]() . (2.62)
. (2.62)
Первым корнем этого уравнения является χ1а=2,405. Ему соответствуют две волны Н01 и E01. Второму корню уравнения (2.62) соответствует следующая пара мод Н02 и Е02 и т.д.
В качестве примера значения части корней бесселевых функций Pпт = χ1а в зависимости от порядка функций и корня бесселевой функции, приведены в табл. 2.3.
Таблица 2.3. Значения корней бесселевых функций Pпт
|
Тип волны |
Порядок функций, n |
Pnm для номера корня функции, m |
||
|
1 |
2 |
3 |
||
|
Eom, Hom |
0 |
2,405 |
5,520 |
8,654 |
|
HE11 |
1 |
0,000 |
3,832 |
7,016 |
|
EH1m |
1 |
3,832 |
7,016 |
10,173 |
|
HE2m |
2 |
3,05 |
5,538 |
8,665 |
|
EH2m |
2 |
5,136 |
8,417 |
11,620 |
Таким образом, функции Бесселя первого рода п-гo порядка дают бесконечное число корней. Причем корни функции J0(χ1а) определяют структуру поля симметричных волн (Eom,Hom), а Jп(χ1а) при п≠0 структуру несимметричных гибридных волн (EНom,HЕom). В индексе моды п — число изменений поля по диаметру, а т — число изменений поля по периметру сердцевины ОВ.
Симметричные волны электрические Eom и магнитные Hom имеют круговую симметрию (n=0). Раздельное распространение по световоду несимметричных волн типа Епт и Нпт невозмоно. В ОВ они существуют только совместно, т.е. имеются продольные составляющие Е и Н. Эти волны называются гибридными, дипольными и обозначаются через НЕпт, если поле в поперечном сечении напоминает поле Н, или Eпт, если поле в поперечном сечении ближе к волнам Е.
2.4.6. Глоговское группирование мод
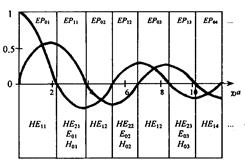
Рис. 2.22. Группирование мод по областям значений между соседними корнями функции J0(χ1а) и J1(χ1а)
Когерентные источники оптического излучения чаще всего создают линейно-поляризованный свет, и поэтому первично в волокне возбуждаются волны, не похожие на НЕ и ЕН волны. Это даже поставило под сомнение правильность индексации указанных волн. Впервые эту трудность разрешил Глог, сгруппировав моды по областям значений χ1а между соседними корнями функций J0(χ1а) и J1(χ1а), как указано на рис. 2.22 и приведено в табл. 2.4.
Суммы полей указанных групп волн дают соответствующие линейно-поляризованные моды, обозначаемые LPпт, или моды поляризации, обозначаемые ЕРпт.
На рис. 2.23 а, б представлены, например, суммы полей волн Н01 с собственным значением χ1а=2,405 и НЕ21 с собственным значением χ21а =3,05, образующих поля двух волн LР11 единой линейной в поперечном сечении ОВ поляризации, указанных стрелками. Аналогично суммы полей волн Е01 и НЕ21 (рис. 2.23 в, г) дают еще две линейные поляризации волны LPпт. Волны LPпт с единой линейной поляризацией представляют собой лишь приближение действительных собственных НЕпт и ЕНпт волн сердечника. Вообще, любая LP1т, волна состоит из Н0т и НЕ2т, волн при одной поляризации и из E0т и НЕ2т волн при другой поляризации. Волна LPпт более высокого порядка и по окружности состоит из волн ЕНп-1,т и НЕп+1,т. Более точно, конечно, использовать спектр волн ЕНпт и НЕпт. Но для слабонаправляюших ОВ с n1≈n2 удобнее использовать LP волны. Только тогда, когда LP волны проходят по ОВ большое расстояние, они расщепляются на собственные НЕ и ЕН волны вследствие различия их собственных значений (фазовых скоростей).
Таблица 2.4. Группирование мод по Глогу
|
Интервал между значениями корней χ1а |
Мода |
Интервал между значениями корней χ1а |
Мода |
|
|
0 – 2,405 |
НЕ11 |
5,520 – 6,380 |
Н02, Е02, НЕ22 |
|
|
2,405 – 3,832 |
Н01, Е01, НЕ21 |
6,380 – 7,016 |
ЕН31, НЕ51 |
|
|
3,832 – 5,136 |
НЕ12, ЕН11, НЕ31 |
7,016 – 7,588 |
НЕ13, ЕН12, НЕ32 |
|
|
5,136 – 5,520 |
ЕН21, НЕ41 |
7,588 – 8,417 |
ЕН41, НЕ61 |
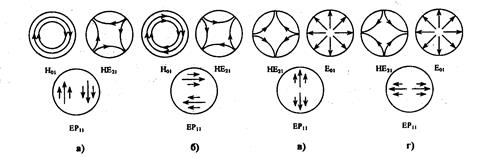
Рис. 2.23. Суммы полей волн Н01 и НЕ21 (Е21 и НЕ21)
Таким образом, при вводе из лазера линейно-поляризованного излучения в ступенчатое оптическое волокно, поддерживающее собственные моды НЕпт и ЕНпт наблюдается их несогласованность как по структуре полей, так и по поляризации. Это приводит к сильному преобразованию волн на начальном участке ОВ и, как следствие, к большим потерям сигналов за счет излучения части их мощности в открытое пространство в виде вытекающих мод. Длина установления равновесного состояния мод может быть определена по приближенной формуле:
![]() (2.63)
(2.63)
и может достигать значений от единиц сантиметров до сотен метров. Например, в случае типичного многомодового ОВ с радиусом сердцевины а=25 мкм, θкр=0,14 и v=30, Ly =300 м.
Картина высвечивания вытекающих мод на участке установления равновесного состояния мод представлена на рис. 2.24. Под Lу понимается длина ОВ, на которой излучается 0,9 мощности всех вытекающих мод.
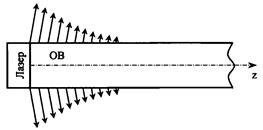
Рис. 2.24. Высвечивание вытекающих мод из МОВ на участке Ly

