В настоящее время практическая радиотехника использует множество различных сигналов. Прежде, чем приступать к их изучению, необходимо определить понятие «сигнал» и охарактеризовать его общие свойства.
Назовём сигналом изменяющуюся физическую величину, отображающую передаваемое сообщение. В качестве таких величин могут выступать ток, напряжение, электромагнитное поле, световой поток и др. Иными словами, сигнал выступает как материальный носитель информации.
При теоретических исследованиях используют математические модели сигналов. В самом общем виде математическая модель сигнала представляет собой функцию ![]() аргумента времени
аргумента времени ![]() . Следует отметить, что математическая модель не учитывает конкретную физическую природу сигнала. Одной и той же математической моделью может быть описано изменение во времени и напряжения, и интенсивности светового потока, и напряжённости электромагнитного поля.
. Следует отметить, что математическая модель не учитывает конкретную физическую природу сигнала. Одной и той же математической моделью может быть описано изменение во времени и напряжения, и интенсивности светового потока, и напряжённости электромагнитного поля.
Все сигналы как физические процессы являются материальными и описываются вещественными функциями. Вместе с тем, при теоретических исследованиях часто удобно описывать сигналы комплексными функциями.
Вид функции ![]() определяет форму сигнала.
определяет форму сигнала.
Как функция времени сигнал может быть определён как на конечном, так и на бесконечном интервале времени. Реальные сигналы всегда конечны. Если сигнал ![]() определён на интервале
определён на интервале ![]() , то величина
, то величина ![]() называется длительностью сигнала. Такие сигналы получили название финитных сигналов. При теоретическом анализе сигнал может быть определён как на бесконечном
называется длительностью сигнала. Такие сигналы получили название финитных сигналов. При теоретическом анализе сигнал может быть определён как на бесконечном ![]() , так и на полубесконечном
, так и на полубесконечном ![]() интервале времени.
интервале времени.
Т.к. сигнал является материальным носителем информации, он обладает энергетическими характеристиками. К основным энергетическим характеристикам относится энергия сигнала
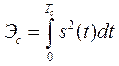 , (1.6)
, (1.6)
и средняя мощность
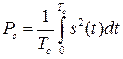 . (1.7)
. (1.7)
Отметим, что если ![]() представляет собой изменение напряжения во времени, энергия сигнала, выделяемая при нагрузке в 1 Ом имеет размерность
представляет собой изменение напряжения во времени, энергия сигнала, выделяемая при нагрузке в 1 Ом имеет размерность ![]() , а средняя мощность в
, а средняя мощность в ![]() .
.
Таким образом, в общем случае сигнал характеризуется формой, длительностью, энергией и средней мощностью.
Изменение сигнала во времени может происходить неслучайным (детерминированным), либо случайным образом. В соответствии с этим сигналы подразделяются на детерминированные и случайные.
К детерминированным сигналам относятся сигналы, значения которых в любой момент времени ![]() полностью известны. Детерминированным сигналом, например, является гармоническое колебание с постоянными на интервале
полностью известны. Детерминированным сигналом, например, является гармоническое колебание с постоянными на интервале ![]() амплитудой, частотой и начальной фазой. Детерминированные сигналы не переносят информации и являются вспомогательными при различных преобразованиях сигналов. С другой стороны, детерминированные сигналы являются удобной моделью при анализе радиотехнических систем.
амплитудой, частотой и начальной фазой. Детерминированные сигналы не переносят информации и являются вспомогательными при различных преобразованиях сигналов. С другой стороны, детерминированные сигналы являются удобной моделью при анализе радиотехнических систем.
Случайные сигналы – это сигналы, значения которых в любой момент времени точно предсказать невозможно. Математическими моделями случайных сигналов являются случайные процессы. Собственно говоря, информация содержится в случайных изменениях физических величин. С другой стороны, моделями случайных процессов описываются и помехи в линии связи. Всё это определяет важность изучения случайных сигналов.
Сигнал ![]() , как уже подчёркивалось выше, представляет собой изменяющуюся во времени величину и с этой точки зрения характеризуется множеством
, как уже подчёркивалось выше, представляет собой изменяющуюся во времени величину и с этой точки зрения характеризуется множеством ![]() значений и множеством моментов времени
значений и множеством моментов времени ![]() , которые она может принимать эти значения. Как множество
, которые она может принимать эти значения. Как множество ![]() , так и множество
, так и множество ![]() может быть непрерывным (континуальным) или дискретным (счётным). Положим эти два признака в основу классификации сигналов.
может быть непрерывным (континуальным) или дискретным (счётным). Положим эти два признака в основу классификации сигналов.
На рис. 1.2 представлены графики изменения величины ![]() в зависимости от моментов времени
в зависимости от моментов времени ![]() в координатах
в координатах ![]()
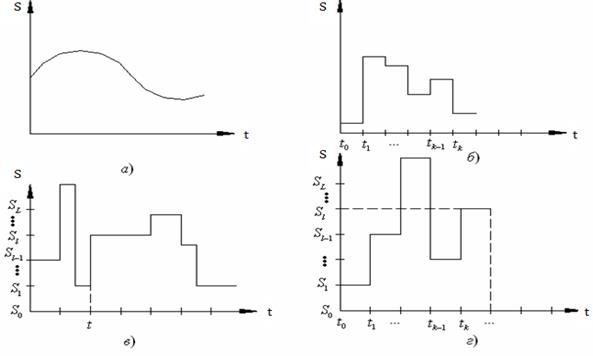
Рис. 1.2
Если множества ![]() и
и ![]() являются непрерывными множествами, т.е. в любой момент времени
являются непрерывными множествами, т.е. в любой момент времени ![]() сигнал может принимать любое значение из множества
сигнал может принимать любое значение из множества ![]() , то такие сигналы называют аналоговыми (непрерывными) сигналами (рис. 1.2, а). Аналоговые сигналы имеют место на выходе микрофона, датчика температуры или давления и т.д.
, то такие сигналы называют аналоговыми (непрерывными) сигналами (рис. 1.2, а). Аналоговые сигналы имеют место на выходе микрофона, датчика температуры или давления и т.д.
Если множество ![]() непрерывно, а множество
непрерывно, а множество ![]() дискретно, т.е. сигнал может принимать любое значение из множества
дискретно, т.е. сигнал может принимать любое значение из множества ![]() но в строго фиксированные моменты времени
но в строго фиксированные моменты времени ![]() , или
, или ![]() , то такие сигналы называются дискретными (рис 1.2, б). Здесь черта обозначает, что
, то такие сигналы называются дискретными (рис 1.2, б). Здесь черта обозначает, что ![]() принимает значения от
принимает значения от ![]() до
до ![]() . Примером дискретного сигнала может служить отражённый от цели сигнал на входе приёмника радиолокационной станции. Действительно, моменты времени
. Примером дискретного сигнала может служить отражённый от цели сигнал на входе приёмника радиолокационной станции. Действительно, моменты времени ![]() определяются временем оборота антенны, а значения
определяются временем оборота антенны, а значения ![]() сигнал может принимать любые, т.к. цель может иметь произвольное положение в пространстве.
сигнал может принимать любые, т.к. цель может иметь произвольное положение в пространстве.
Если множество значений ![]() дискретно, а множество моментов времени
дискретно, а множество моментов времени ![]() непрерывно, т.е. сигнал принимает строго фиксированные значения
непрерывно, т.е. сигнал принимает строго фиксированные значения ![]() в любой произвольный момент времени
в любой произвольный момент времени ![]() , или
, или ![]() , то такие сигналы называются квантованными (рис. 1.2, в). К квантованным сигналам можно отнести сигнал на выходе контролёра-автомата метрополитена. Число пассажиров, которые проходят через контролёр - автомат всегда принимает целые значения, а значения моментов времени произвольные.
, то такие сигналы называются квантованными (рис. 1.2, в). К квантованным сигналам можно отнести сигнал на выходе контролёра-автомата метрополитена. Число пассажиров, которые проходят через контролёр - автомат всегда принимает целые значения, а значения моментов времени произвольные.
И, наконец, если множества ![]() и
и ![]() дискретны, то такие сигналы
дискретны, то такие сигналы ![]() называются цифровыми (рис. 1.2, г). Своё название такие сигналы получили ввиду того, что значения
называются цифровыми (рис. 1.2, г). Своё название такие сигналы получили ввиду того, что значения ![]() сигнала и моменты
сигнала и моменты ![]() времени изменений значений могут быть представлены числами натурального ряда. Примерами цифровых сигналов могут служить сигналы, которыми обмениваются устройства ЭВМ, сигналы телексной связи и другие.
времени изменений значений могут быть представлены числами натурального ряда. Примерами цифровых сигналов могут служить сигналы, которыми обмениваются устройства ЭВМ, сигналы телексной связи и другие.
Отметим, что в дискретном и цифровом сигналах значения ![]() сохраняются в течение интервала времени
сохраняются в течение интервала времени ![]() неизменным. Если значения сигнала фиксировать в моменты времени
неизменным. Если значения сигнала фиксировать в моменты времени ![]() короткими импульсами
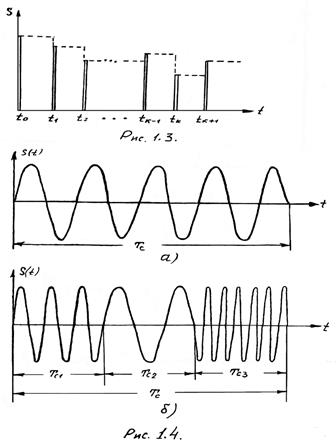
короткими импульсами ![]() , то такие сигналы называются импульсными (рис. 1.3).
, то такие сигналы называются импульсными (рис. 1.3).
Для сравнений на рисунке пунктирными линиями показан дискретный сигнал, соответствующий импульсному сигналу. В ряде случаев значения импульсного сигнала называют отсчётами.
Продолжим классификацию сигналов. Если на интервале времени ![]() сигнал описывается одной элементарной функцией времени, то такой сигнал называется простым (элементарным) сигналом (рис. 1.4,а).
сигнал описывается одной элементарной функцией времени, то такой сигнал называется простым (элементарным) сигналом (рис. 1.4,а).
Если же на этом интервале времени сигнал описывается совокупностью простых сигналов, например,
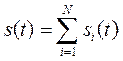 ,
,
где ![]() имеет длительность
имеет длительность ![]() , то такие сигналы называют составными (или сложными).
, то такие сигналы называют составными (или сложными).
На рис. 1.4, б изображён составной сигнал, образованный совокупностью трёх простых сигналов описываемых гармоническими функциями.
И, наконец, в связи с широким использованием цифровых сигналов в современных РТИС, остановимся на понятии ансамбля сигналов. Ввиду того, что в цифровых РТИС число значений первичных сигналов ![]() ограничено, для их передачи можно использовать конечное число сигналов
ограничено, для их передачи можно использовать конечное число сигналов ![]() . Совокупность таких сигналов образуют ансамбль сигналов. Важнейшей характеристикой ансамбля сигналов является его объем
. Совокупность таких сигналов образуют ансамбль сигналов. Важнейшей характеристикой ансамбля сигналов является его объем ![]() , т.е. число сигналов, входящих в ансамбль. От этого показателя зависит информативность каждого сигнала в отдельности и ансамбля в целом, способность противостоять помехам, время доведения сообщений до получателя т.е. все то, что определяет эффективность радиотехнической информационной системы.
, т.е. число сигналов, входящих в ансамбль. От этого показателя зависит информативность каждого сигнала в отдельности и ансамбля в целом, способность противостоять помехам, время доведения сообщений до получателя т.е. все то, что определяет эффективность радиотехнической информационной системы.
И в заключение отметим, что понятие ансамбля сигналов может быть распространенно и на совокупность ансамбля сигналов.

