Рассмотрим применение классического метода к расчету переходных процессов в цепях первого порядка. Это цепи, содержащие только однотипные реактивные элементы (емкости или индуктивности), процессы, в которых описываются дифференциальными уравнениями первого порядка (6.10)

Примером цепей первого порядка являются простейшие RL и RC цепи.

Переходные процессы в RL-цепях

Рассмотрим включение RL-цепи к источнику напряжения u(t) (рис. 6.1).

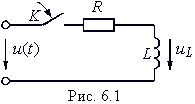
Из рис. 6.1 следует, что до коммутации ключ К разомкнут, поэтому ток i_L(0_–) = 0 и цепь находится при нулевых начальных условиях. В момент t = 0 ключом К замыкаем (осуществим коммутацию) цепь, подключив ее к источнику напряжения u(t). После замыкания ключа К в цепи начнется переходный процесс. Для его математического описания выберем в качестве независимой переменной i_L = i и составим относительно нее дифференциальное уравнение по ЗНК: (6.11)

Уравнение (6.11) относится к линейным неоднородным дифференциальным уравнениям первого порядка типа (6.3), решение которого можно записать согласно (6.5) в форме (6.12) где i_св — свободная составляющая тока, обусловленная свободными процессами, протекающими в цепи без участия источника u(t); i_np — принужденная составляющая тока, обусловленная действием источника напряжения u(t).

Свободная составляющая тока i_св есть общее решение однородного дифференциального уравнения (6.13) и согласно (6.7) (6.14) где А — постоянная интегрирования; р — корень характеристического уравнения типа (6.6); (6.15)

Отсюда p = —R/L. Величина 1/|р| носит название постоянной времени цепи. В неразветвленной RL-цепи = L/R.

Принужденная составляющая i_пp может быть определена как частное решение уравнения (6.11). Однако, как было указано выше, i_пp можно найти более просто методами расчета установившегося режима цепи. Рассмотрим два частных случая:

В первом случае принужденная составляющая может быть определена из установившегося режима: i_пp = U/R. Для нахождения постоянной интегрирования A перепишем (6.12) в форме i = Ае^{–t /} + U/R и учтем начальные условия для i, а также первый закон коммутации (6.1):

Отсюда А = —U/R. Таким образом, закон изменения тока в RL-цепи определяется уравнением (6.16)

Напряжение на индуктивности согласно (1.9) (6.17)

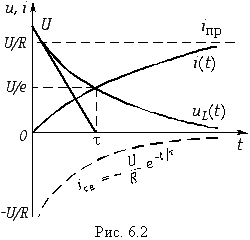
На рис. 6.2 изображены графики зависимости i(t) и u_L(t). Анализ полученных уравнений (6.16) и (6.17) показывает, что чем больше постоянная времени цепи , тем медленнее затухает переходной процесс. На практике принято считать переходной процесс законченным при t = (3...5), при t = 3 ток достигает 95% своего установившегося значения, а при t = 5 — более 99%. Графически постоянная времени может определиться как интервал времени на оси t от t = 0 до точки пересечения касательной к u_L (рис. 6.2), в указанный момент напряжение на u_L уменьшается в е раз по сравнению с начальным.

Анализ полученных результатов показывает, что при нулевых начальных условиях в момент t = 0₊ индуктивность ведет себя как бесконечно большое сопротивление (разрыв цепи), а при t = как бесконечно малое сопротивление (короткое замыкание цепи).

Для второго случая принужденная составляющая тока где , = arctg(L/R). Постоянная интегрирования определяется из уравнения

Откуда . Следовательно, закон изменения тока в цепи в этом случае будет (6.18)

На рис. 6.3 изображена временная зависимость тока (6.18). Напряжение на индуктивности 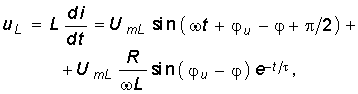(6.19) где U_mL = LI_m.

Анализ уравнения (6.18) показывает, что в случае подключения цепи к источнику u(t) в момент, когда _u = ± /2 в последней могут возникать сверхтоки. Если постоянная времени цепи достаточно велика, то скачок тока в начальный период может достигать i_max 2I_m. Напротив, при включении цепи в момент, когда _u = , в ней сразу наступает установившийся режим. Аналогичная картина наблюдается и с напряжением на индуктивности (6.19).

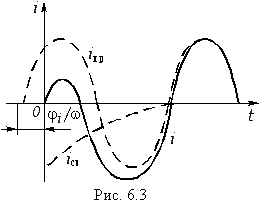
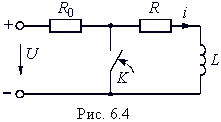
В качестве второго примера расчета рассмотрим случай ненулевых начальных условий в RL-цепи (рис. 6.4). К моменту коммутации в данной цепи была запасена энергия магнитного поля, равная W_L = Li²(0_– )/2, где i(0_– ) = U/(R₀ + R). После коммутации в RL-цепи возникает переходный процесс, описываемый уравнением: (6.20) т. е. i_пp = 0. Решая уравнение (6.20), находим с учетом (6.13) – (6.15):

Постоянную А находим из начального условия i(0_– ) и закона коммутации (6.1):

Окончательно закон изменения тока в переходном режиме описывается уравнением 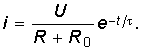(6.21)

Напряжение u_L определяется как 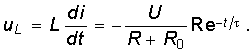(6.22)

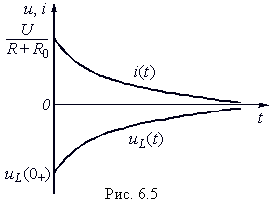
На рис. 6.5 изображены графики i и u_L. Следует отметить, что вся энергия W_L, запасенная в индуктивности с течением времени, расходуется на тепловые потери в R. При ненулевых начальных условиях L ведет себя как источник тока.

Переходные процессы в RС-цепях

При расчете переходных процессов в RС-цепях в качестве независимой переменной выбирают u_C. Затем также составляют дифференциальное уравнение для заданной RС-цепи, решение которого с учетом начальных условий для u_C(0) и определяет закон изменения напряжения на емкости.

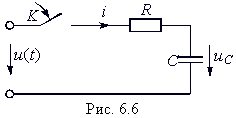
Рассмотрим вначале RC-цепь при нулевых начальных условиях (рис. 6.6), которая подключается в момент t = 0 к источнику постоянного и(t) = U или синусоидального и(t) = U_msin(t + _u ) напряжения. Переходный процесс в данной цепи описывается дифференциальным уравнением (6.23) решение которого ищем также в форме суммы общего и частного решений, определяющих свободную и принужденную составляющие: (6.24)

Свободная составляющая является решением однородного дифференциального уравнения 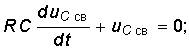(6.25) (6.26) где р определяется из характеристического уравнения

Величина RC носит название постоянной времени RC-цепи и обозначается через .

Определим принужденную составляющую u_{C пp} для случая, когда u(t) = U = const. Из рис. 6.6 следует, что в установившемся режиме u_{C пp} = U. Следовательно, с учетом (6.24) и (6.26) уравнение для и_C примет вид и_C = Ae^{–t /} + U. Для нахождения постоянной интегрирования А учтем нулевые начальные условия для u_C(0_–) и второй закон коммутации (6.2): u_C(0_–) = u_C(0₊) = 0 = A + U, откуда А = —U. Таким образом, получаем окончательно: (6.27)

Ток в цепи определяется согласно (1.12): (6.28)

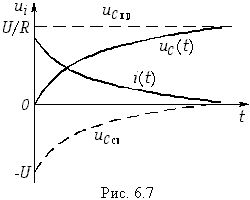
На рис. 6.7 изображены графические зависимости u_С(t) и i(t).

Анализ полученных результатов показывает, что в момент t = 0₊ емкость С (при нулевых начальных условиях) ведет себя как короткозамкнутый участок. Напротив, при t = емкость представляет собой бесконечно большое сопротивление (разрыв цепи для постоянного тока).

Рассмотрим случай гармонического воздействия. Нетрудно видеть что при этом (6.29) где 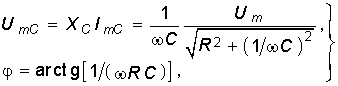(6.30) а напряжение

Постоянная А находится из начальных условий для u_C(0₊) при t = 0₊:

Окончательно закон изменения напряжения 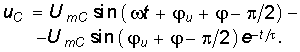(6.31)

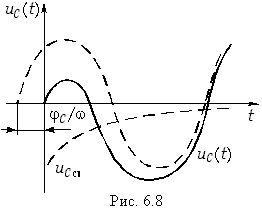
На рис. 6.8 изображен график зависимости u_C(t). Анализ уравнения (6.31) показывает, что в случае неудачного включения при _u = – и большой в цепи могут возникать перенапряжения, достигающие на емкости величины u_Cmax 2U_mC. В случае удачного включения, когда _u = /2 – , в цепи сразу наступает установившийся режим.

Ток в цепи 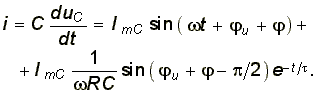(6.32)

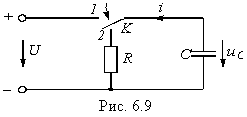
Рассмотрим теперь случай ненулевых начальных условий, когда емкость С, заряженная до напряжения U, разряжается на сопротивление R (рис. 6.9). К моменту коммутации в емкости была запасена энергия W_C = CU²/2. После коммутации возникает переходный процесс, определяемый уравнением (6.33) т. е. имеет место свободный режим разряда (емкости): (6.34)

Постоянную интегрирования А находим из начального условия для u_C(0₊) = U и закона коммутации (6.2):

Таким образом, получаем закон изменения напряжения на емкости (6.35) и тока в цепи (6.36)

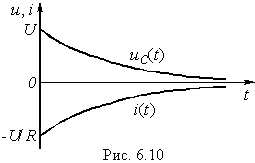
Знак "–" в уравнении (6.36) для тока свидетельствует о том, что ток разряда направлен противоположно опорному направлению напряжения и_С в емкости. На рис. 6.10 приведены графики изменения напряжения и_С(t) и тока i(t) данной RС-цепи. Следует подчеркнуть, что вся запасенная энергия W_C емкости с течением времени преобразуется в элементе R в тепло. При ненулевых начальных условиях С ведет себя как источник напряжения.